常见的类别变量的有调节的中介模型分析*

方 杰 温忠麟 何子杰

（1.广东财经大学新发展研究院/应用心理学系，广州 510320；2.华南师范大学心理学院/心理应用研究中心，广州 510631；3.广东财经大学经济学院，广州 510320）

有调节的中介模型（moderated mediation model）意味着自变量X 通过中介变量M对因变量Y 产生影响，而中介过程（X→M→Y）受到调节变量Z 的调节（温忠麟，叶宝娟，2014），图1（a）是模型概念图。有调节的中介模型分析既要检验中介效应（即X→M→Y 的间接影响）是否受到调节变量Z 的调节，还要检验直接效应（即X→Y 的直接影响）是否受到调节变量Z 的调节（图1（a））。以往的有调节的中介模型研究几乎都假设X 和Z 是连续变量的情况，但当X或Z 是类别变量（M 和Y 是连续变量），如何进行有调节的中介模型分析呢？如果自变量或调节变量为二分类别变量，可将类别变量进行0 和1 编码，仍可使用连续变量的有调节的中介模型分析方法进行分析（温忠麟，刘红云，2020）。但如果自变量或调节变量为k 个类别（k≥3），问题就变得复杂了。

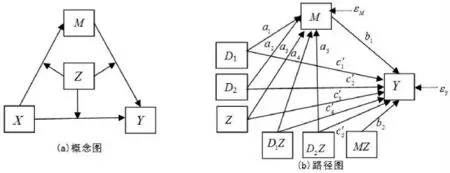
图1 类别自变量的两阶段被调节的中介模型图

第一，当自变量是连续变量或二分类别变量时，只有一个中介效应；但当自变量是多类别（k≥3）时，则会有k-1 个相对中介效应（方杰等，2017），也就需要考察k-1个相对中介效应是否被调节（即要检验k-1 次），这就增加了问题的复杂性。

第二，有调节的中介模型分为三类，即第一阶段（X→M）被调节、第二阶段（M→Y）被调节和两阶段被调节的中介模型，需要考察的相对中介效应的数目变为3×（k-1），这进一步增加了问题的复杂性。

第三，有多种方法可以检验中介效应是否被调节，温忠麟等（2014）系统总结了有调节的中介效应的三种检验方法，即依次检验、系数乘积的区间检验和中介效应差异检验。那么，当自变量或调节变量为多类别时，在何种情境下应选择何种检验方法更合适呢？

第四，当自变量是多类别（k≥3）时，相对直接效应也从1 个增加为k-1 个（方杰等，2017），如何检验k-1 个相对直接效应是否被调节呢？

第五，当调节变量是多类别（k≥3）时，则会有k 个中介效应和k 个直接效应。如何检验k 个中介效应是否被调节呢？k 个直接效应是否被调节呢？

这些问题都困扰着应用研究者，直接导致了类别变量的有调节的中介模型分析的实际应用还很少。本文将以三类别的两阶段被调节的中介模型为例，详述如何正确地进行类别自变量或类别调节变量的有调节的中介模型分析；然后，用一个实例说明如何进行类别变量的有调节的中介模型分析；最后对相关议题做了讨论和拓展。

1 类别自变量的两阶段被调节的中介模型分析

三类别自变量（其余变量皆为连续变量）的两阶段被调节的中介模型（见图1）的分析过程是：

第一，对自变量进行虚拟编码。由于自变量存在3 个水平，因此研究者可根据研究目的选择自变量的某个水平为参照水平，产生2 个虚拟变量（D1和D2）（见图1（b））

第二，两阶段被调节的中介效应分析执行如下回归方程：

相对参考水平而言，D1→M→Y 的相对中介效应是（a1+a4Z）（b1+b2Z），如果（a1+a4Z）（b1+b2Z）的Bootstrap 置信区间不包含0，表示D1→M→Y 的相对中介效应显著。调节变量Z 的取值区间内的最大值为Zmax、最小值为Zmin，如果（a1+a4Zmax）（b1+b2Zmax）-（a1+ a4Zmin）（b1+b2Zmin）的Bootstrap 置信区间不包含0，就表示D1→M→Y 的相对中介效应受到Z的调节（温忠麟，叶宝娟，2014）。相对参考水平而言，D2→M→Y 的相对中介效应是（a2+a5Z）（b1+b2Z），如果（a2+a5Z）（b1+b2Z）的Bootstrap 置信区间不包含0，表示D2→M→Y的相对中介效应显著。如果（a2+a5Zmax）（b1+b2Zmax）-（a2+a5Zmin）（b1+b2Zmin）的Bootstrap 置信区间不包含0，就表示D2→M→Y 的相对中介效应受到Z 的调节。

同理，相对参考水平而言，D1→Y 的相对直接效应是c1′+c4′Z，如果c1′+c4′Z 的Bootstrap 置信区间不包含0，表示D1→Y的相对直接效应显著。更进一步，如果相对直接效应之差（c1′+c4′Zmax）-（c1′+c4′Zmin）显著不等于0，就表示D1→Y 的相对直接效应受到Z 的调节。因为两个直接效应之差（c1′+c4′Zmax）-（c1′+c4′Zmin）=c4′（Zmax-Zmin），当利用Bootstrap 法获得c4′（Zmax-Zmin）的置信区间时，Zmax-Zmin在所有Bootstrap 样本中都为常数，所以c4′的Bootstrap 置信区间不包含0，就表示D1→Y 的相对直接效应受到Z的调节（方杰等，2014）。相对参考水平而言，D2→Y 的相对直接效应是c2′+c5′Z，如果c2′+c5′Z 的Bootstrap 置信区间不包含0，表示D2→Y 的相对直接效应显著。如果c5′的Bootstrap 置信区间不包含0，表示D2→Y 的相对直接效应受到Z 的调节。如果不考虑直接效应是否被Z 调节，则去掉方程（2）中的c4′D1Z 和c5′D2Z。

2 类别调节变量的两阶段被调节的中介模型分析

三类别调节变量（其余变量皆为连续变量）的两阶段被调节的中介模型（见图2）的分析过程是：

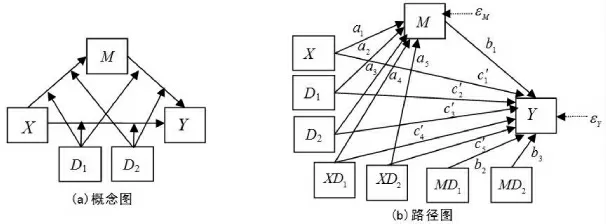
图2 类别调节变量的两阶段被调节的中介模型图

第一，对调节变量进行虚拟编码（见图2（b）），编码方法与类别自变量的编码方法一样，不再赘述。

第二，两阶段被调节的中介效应分析执行如下回归方程：

当调节变量Z 为参考水平时（D1=D2=0），中介效应是a1b1，直接效应是c1′。当调节变量Z 为D1时（D1=1 且D2=0），中介效应是（a1+a4）（b1+b2），直接效应是c1′+c4′。当调节变量Z 为D2时（D1=0 且D2=1），中介效应是（a1+a5）（b1+b3），直接效应是c1′+c5′。如果a1b1、（a1+a4）（b1+b2）、（a1+a5）（b1+b3）的Bootstrap 置信区间不包含0，则表示中介效应显著。如果c1′、c1′+c4′、c1′+c5′的Bootstrap置信区间不包含0，则表示直接效应显著。

调节变量Z 为D1和参考水平的中介效应之差为（a1+a4）（b1+b2）-a1b1=a1b2+a4b1+a4b2，如果a1b2+a4b1+a4b2的Bootstrap 置信区间不包含0，则表示中介效应受到Z 的调节。调节变量Z 为D2和参考水平的中介效应之差为（a1+a5）（b1+b3）-a1b1=a1b3+a5b1+a5b3，如果a1b3+a5b1+a5b3的Bootstrap 置信区间不包含0，则表示中介效应受到Z 的调节。

调节变量Z 为D1和参考水平的直接效应之差为（c1′+c4′）-c1′=c4′，如果c4′的Bootstrap 置信区间不包含0，则表示直接效应受到Z 的调节。调节变量Z 为D2和参考水平的直接效应之差为（c1′+c5′）-c1′=c5′，如果c5′的Bootstrap 置信区间不包含0，则表示直接效应受到Z 的调节。如果不考虑直接效应是否被Z 调节，则去掉方程（4）中的c4′XD1和c5′XD2。

3 示 例

接下来用一个例子演示如何进行类别变量的有调节的中介模型分析。本例感兴趣的是，公正感（X）通过负性情绪（M）影响员工偏离行为（Y）的中介过程，是否受到了性别（Z）的调节，模型如图1 所示。本例的所有变量及其数据均来自方杰等（2017）。自变量公正感是类别变量（分为低、中、高三水平），采用虚拟编码，产生2 个虚拟变量（D1和D2）。低公正感为参照水平，编码为D1=0 和D2=0；中等公正感编码为D1=1和D2=0；高公正感编码为D1=0 和D2=1。中介变量负性情绪和因变量员工偏离行为是连续变量，调节变量为性别（0 表示女，1 表示男）。我们使用SPSS 软件运行PROCESS 3.4的模型59（PROCESS 还可在SAS 和R软件上运行），进行两阶段被调节的中介模型分析。分析结果如表1 所示。模型1 对应方程（1），模型2 对应方程（2）。具体分析如下：

表1 三类别自变量的两阶段被调节的中介效应分析结果

3.1 有调节的中介效应分析

在性别为女（Z=0）时，相对于低公正感，中等公正感的相对中介效应a1b1为-0.033，SE=0.061，95%的 非 参 数 百 分 位Bootstrap 法的置信区间［-0.154，0.085］，包含0，相对中介效应不显著。在性别为男（Z=1）时，相对于低公正感，中等公正感的相对中介效应（a1+a4）（b1+b2） 为-0.346，SE=0.106，95%的非参数百分位Bootstrap法的置信区间［-0.559，-0.145］，不包含0，相对中介效应显著。男女中介效应的差（a1+a4）（b1+b2）-a1b1=a1b2+a4b1+a4b2=-0.313，SE=0.120，95%的非参数百分位Bootstrap法的置信区间［-0.554，-0.079］，不包含0，由此得出结论，相对于低公正感，中等公正感的相对中介效应受到性别的调节。

在性别为女（Z=0）时，相对于低公正感，高公正感的相对中介效应a2b1为-0.262，SE=0.071，95%的 非 参 数 百 分 位Bootstrap 法的置信区间［-0.413，-0.134］，不包含0，相对中介效应显著。在性别为男（Z=1）时，相对于低公正感，高公正感的相对中介效应（a2+a5）（b1+b2）为-0.823，SE=0.108，95%的非参数百分位Bootstrap 法的置信区间［-1.045，-0.619］，不包含0，相对中介效应显著。男女中介效应的差（a2+a5）（b1+b2）-a2b1= a2b2+a5b1+a5b2= -0.561，SE=0.128，95%的非参数百分位Bootstrap法的置信区间［-0.811，-0.311］，不包含0，由此得出结论，相对于低公正感，高公正感的相对中介效应受到性别的调节。

3.2 有调节的直接效应分析

在性别为女（Z=0）时，相对于低公正感，中等公正感的相对直接效应c1′为-0.24，SE=0.134，95% 的 非 参 数 百 分 位Bootstrap 法的置信区间［-0.504，0.021］，包含0，相对直接效应不显著。在性别为男（Z=1）时，相对于低公正感，中等公正感的相对直接效应c1′+c4′为-0.33，SE= 0.139，95%的非参数百分位Bootstrap 法的置信区间［-0.605，-0.059］，不包含0，相对直接效应显著。男女直接效应的差c4′为-0.09，SE=0.193，95%的非参数百分位Bootstrap法的置信区间［-0.469，0.289］，包含0，表明相对于低公正感，中等公正感的相对直接效应没有受到性别的调节。

在性别为女（Z=0）时，相对于低公正感，高公正感的相对直接效应c2′为-0.33，SE=0.126，95%的非参数百分位Bootstrap法的置信区间［-0.581，-0.086］，不包含0，相对直接效应显著。在性别为男（Z=1）时，相对于低公正感，高公正感的相对直接效应c2′+c5′为-0.83，SE=0.136，95%的非参数百分位Bootstrap 法的置信区间［-1.090，-0.556］，不包含0，相对直接效应显著。男女直接效应的差c5′为-0.49，SE=0.185，95%的非参数百分位Bootstrap 法的置信区间［-0.853，-0.126］，不包含0，表明相对于低公正感，高公正感的相对直接效应受到性别的调节。

需要说明的是，虽然示例使用了PROCESS 插件进行数据分析，实际上还可以使用Mplus 软件对示例数据进行类别变量的有调节的中介效应分析。具体地，先将示例数据的三类别自变量进行虚拟变量编码，产生D1和D2两个新变量，然后利用Mplus 程序（见图3）进行有调节的中介模型分析，分析结果与PROCESS 的分析结果一致，不再赘述。

图3 类别自变量的两阶段被调节的中介模型分析的Mplus 程序

4 讨论与拓展

类别变量在心理学和其他社科领域研究中经常遇到，已有文献讨论了类别变量的中介和调节分析方法（方杰等，2017；方杰，温忠麟，2022），但如果将中介和调节整合在一起，进行类别变量的有调节的中介模型分析，问题就变得复杂了。本文试图为应用研究者提供相应的方法学支持。在阐述了类别变量的两阶段被调节的中介模型的分析方法后，用示例演示如何进行分析。但是，本文介绍的方法尚有不足，有待进一步研究和拓展。

4.1 模型拓展

本文只涉及两阶段被调节的中介模型，实际上本文的步骤和方法同样适用于第一阶段（X→M）、第二阶段（M→Y）被调节的中介模型和有中介的调节模型。

4.1.1 第一阶段被调节的中介模型

如果是类别自变量的第一阶段被调节的中介模型，只需要方程（2）去掉b2MZ 即可。相对参考水平而言，D1→M→Y 的相对中介效应变为（a1+a4Z）b1，如果a4b1的Bootstrap 置信区间不包含0，就表示D1→M→Y 的相对中介效应受到Z 的调节。相对参考水平而言，D2→M→Y 的相对中介效应变为（a2+a5Z）b1，如果a5b1的Bootstrap 置信区间不包含0，就表示D2→M→Y 的相对中介效应受到Z 的调节。相对参考水平而言，如果c4′或（和）c5′的Bootstrap 置信区间不包括0，就表示D1→Y 或（和）D2→Y 的相对直接效应受到Z 的调节（Hayes，2018）。

如果是类别调节变量的第一阶段被调节的中介模型，只需要方程（4）去掉b2MD1和b3MD2即可。此时，调节变量Z 为D1时的中介效应变为（a1+a4）b1，Z 为D2时的中介效应变为（a1+a5）b1，如果a4b1或a5b1的Bootstrap 置信区间不包含0，则表示中介效应受到Z 的调节，如果c4′或c5′的Bootstrap置信区间不包含0，则表示直接效应受到Z的调节。

4.1.2 第二阶段被调节的中介模型

如果是类别自变量的第二阶段被调节的中介模型，只需要方程（1）去掉a3Z、a4D1Z和a5D2Z 即可。相对参考水平而言，D1→M→Y 的相对中介效应变为a1（b1+b2Z），如果a1b2的Bootstrap 置信区间不包含0，就表示D1→M→Y 的相对中介效应受到Z 的调节。相对参考水平而言，D2→M→Y 的相对中介效应变为a2（b1+b2Z），如果a2b2的Bootstrap 置信区间不包含0，就表示D2→M→Y 的相对中介效应受到Z 的调节。相对参考水平而言，如果c4′或（和）c5′的Bootstrap 置信区间不包括0，就表示D1→Y或（和）D2→Y 的相对直接效应受到Z 的调节。

如果是类别调节变量的第二阶段被调节的中介模型，只需要方程（3）去掉a2D1、a3D2、a4XD1和a5XD2即可。此时，调节变量Z为D1时的中介效应变为a1（b1+b2），Z 为D2时的中介效应变为a1（b1+b3），如果a1b2或a1b3的Bootstrap 置信区间不包含0，则表示中介效应受到Z 的调节，如果c4′或c5′的Bootstrap 置信区间不包含0，则表示直接效应受到Z 的调节。

4.1.3 有中介的调节模型

本文只涉及有调节的中介模型。实际上还有一种中介和调节的整合模型，即有中介的调节模型。有中介的调节模型可分为两种，一种是有中介的调节模型Ι，即调节变量Z 调节自变量X 和因变量Y 的关系，而这种调节效应至少部分地通过中介变量M 对Y 起作用。有中介的调节模型Ι 的分析步骤与第一阶段被调节的中介模型的分析步骤一致（Edwards & Lambert，2007；温忠麟等，2022；王阳等，2022）。另一种是有中介的调节模型Ⅱ，即Z 先影响M，再由M 调节X 和Y 的关系。有中介的调节模型Ⅱ的分析步骤与第二阶段被调节的中介模型（需将Z 当成自变量、X 当成调节变量）的分析步骤一致（Kwan & Chan，2018；温忠麟等，2022；王阳等，2022）。因此，类别变量的有调节的中介模型的分析步骤和方法可以方便地推广到类别变量的有中介的调节模型分析中。

4.2 变量的拓展

本文的有调节的中介模型都假设因变量是连续变量，实际上本文的步骤和方法都可以拓展到因变量是二分类别变量的情况。具体地，方程（1）和（3）仍然使用多元线性回归，但方程（2）和（4）使用Logistic 回归代替多元线性回归即可。PROCESS 4.0 可以方便地执行二分因变量的有调节的中介效应分析，因此PROCESS 4.0 可分析2（多类别/连续自变量）×2（多类别/连续调节变量）×2（二分类别/连续因变量）×3（调节的中介路径类型）共24 种类别变量的有调节的中介模型。值得注意的是，PROCESS 4.0 在进行二分因变量的有调节的中介效应分析时，直接将系数a 和b 相乘得到中介效应大小，使得中介效应存在量尺不统一的问题，即X→M 的影响a 是连续变量的量尺，M→Y 的影响b 是Logit量尺。已有研究者在二分因变量的简单中介模型的分析中，提出了两种统一量尺的方法（方杰等，2017；刘红云等，2013）。一种方法是将系数b 标准化为bstd（MacKinnon& Dwyer，1993），对a×bstd进行显著性检验；另一种方法是将系数a 和b 各自变为Za=a／SE(a)和Zb=b／SE(b)，再对Za×Zb进行显著性检验（Iacobucci，2012）。这两种方法是否适用于二分因变量的有调节的中介模型，还有待进一步深入研究。

同理，本文的有调节的中介模型也可以推广到中介变量是二分类别变量的情况。具体地，方程（2）和（4）仍然使用多元线性回归，但方程（1）和（3）使用Logistic 回归代替多元线性回归即可，此时也存在量尺不统一的问题。PROCESS 4.0 暂时无法执行二分中介变量的有调节的中介模型分析，此时建议使用SPSS 软件分别执行多元线性回归和Logistic 回归，得到各个系数值及其显著性检验结果，再判断中介效应是否受到调节（温忠麟，叶宝娟，2014；温忠麟，刘红云，2020）。如果因变量和中介变量都是二分类别变量，则方程（1）~（4）都用Logistic 回归代替多元线性回归，此时量尺是统一的，建议用SPSS 软件执行Logistic回归，得到各个系数值及其显著性检验结果，再判断中介效应是否受到调节。

4.3 类别变量的编码方式的拓展

本文仅用虚拟编码［又称为指标编码（indicator code）］对多类别变量进行编码，实际上PROCESS 还提供了另外三种编码方式供研究者选用，即序列编码（sequential code）、效应编码（effect code）和Helmet 编码（见表2）。所有的编码方式都可使用相同的有调节的中介模型的分析步骤和方法。

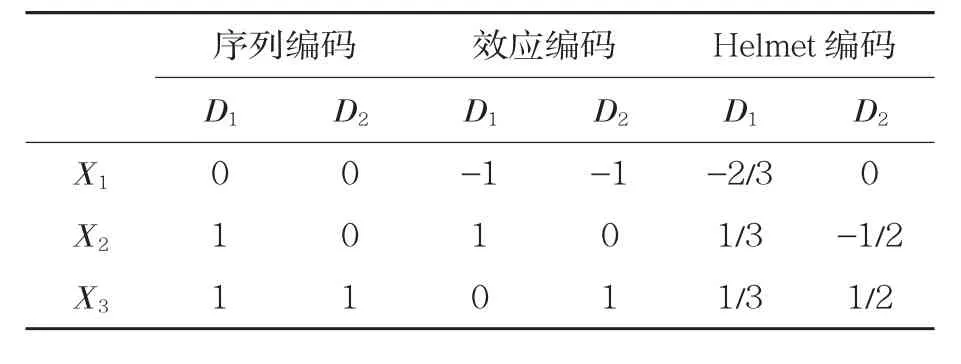
表2 三类别变量的各种编码方式

如果研究者感兴趣的是X1和X2之间的对比以及X1和X3之间的对比，则建议使用虚拟编码。如果研究者感兴趣的是X1和X2之间的对比以及X2和X3之间的对比，则建议使用序列编码。使用示例数据，用序列编码进行两阶段被调节的中介模型分析，结果还发现相对于中等公正感，高公正感的相对中介效应不受性别的调节。

如果自变量是有序类别变量（ordinal categorical variable），则在下述情况下推荐使用Helmet 编码。例如，自变量是新冠疫情下的自我保护程度，包括三个水平：不保护，少量保护（只有自己戴口罩，其他人不戴口罩）和充分保护（全社区人员都戴口罩），保护程度是有序增强，此时推荐使用Helmet 编码。因为此时研究者或许感兴趣的是不保护X1和有保护（X2和X3）之间的对比以及少量保护X2和充分保护X3之间的对比（Hayes，2018）。如果研究者感兴趣的是X2和（X1和X3）之间的对比以及X3和（X1和X2）之间的对比，则建议使用效应编码。因此，建议研究者在阐述结果前，先说明类别变量的编码方式。

5 结 语

目前，类别变量的有调节的中介模型的实际应用还较少，一个较为重要的原因是，应用研究者还不清楚如何正确地进行类别变量的有调节的中介模型分析。表3将常用的类别变量的有调节的中介模型及其分析策略进行了总结，便于应用研究者了解哪些场景或模型应该使用类别变量的有调节的中介模型进行数据分析，并能按图索骥地选择合适的分析策略。

表3 常见的类别变量的有调节的中介模型及其分析策略

另外，虽然本文是以三类别的类别变量为例进行阐述，但本文的方法同样也适用于4 个类别或更多类别的情况，如果自变量是n 个类别，就产生n-1 个虚拟变量（D1、D2、…、Dn-1）和n-1 个相对中介效应，需要检验n-1 个相对中介效应各自是否被调节。同理，还需要检验n-1 个相对直接效应各自是否被调节。如果是五个或五个以上类别的类别变量，实际上可当成连续变量处理（温忠麟，刘红云，2020）。

现在，类别变量的有调节的中介模型分析的方法学研究还处于蓬勃发展阶段，还有诸多问题亟待解决。例如，在多层嵌套数据中，如何进行类别变量的有调节的多层中介模型分析呢？再如，本文仅涉及一个中介变量，如果模型中存在多个中介变量，如何进行类别变量的有调节的多重中介模型分析呢？又如，本文仅涉及因变量或中介变量是二分类别变量的情况，如果因变量或中介变量为多类别变量，如何进行有调节的中介模型分析？相信随着方法研究的深入，会不断增加我们对类别变量的有调节的中介问题的理解。