比色法测定汽车材料中六价铬的不确定度评定

胡曼 晁华 蔡逸飞 王森 曹祝 陈杰

（襄阳达安汽车检测中心有限公司，襄阳 441004）

1 前言

引入测量不确定度的目的是为了更加合理地表征被测量值的分散性，不确定度与测量结果密切相关。为使测量结果能够与标准或规范中给出的参考值进行有效的比较，并能够提供一个便于实现、容易理解和公认的方法来表征测量结果的质量，对测量结果进行不确定度评估十分有必要[1]。在实际的分析工作中，由于定义的不完整、取样方式、基体干扰、环境条件、仪器设备的不确定度、参考值、测量方法和程序中的估计和假定以及随机变化等等系列因素导致的测量结果的不确定性使评定测量结果的不确定度十分重要[2]。汽车行业检测实验室需要对每一项有数值要求的测量结果开展测量不确定度评估[3]。

采用碱液消解方法处理汽车材料，得到可以用于后续分析的样品溶液，采用紫外分光光度法测定汽车材料中六价铬含量，对测试结果进行不确定度评估，分析测量过程中不确定度的来源及其主要影响因素，提高测试结果的准确度和可信度。

2 不确定度评定简介

2.1 评定目的

采用二苯碳酰二肼作为显色剂，应用紫外可见分光光度计在特定波长下对汽车材料中的六价铬含量进行定量检测，并计算其不确定度。

2.2 依据文件

评定执行QC/T 942—2013《汽车材料中六价铬的检测方法》[4]、CNAS-GL06：2006《化学分析中不确定度的评估指南》[5]、JJF1059.1-2012《测量不确定度评定与表示》[6]。

2.3 检测仪器与设备

紫外可见分光光度计，经检定合格；pH 计，经检定合格；电子天平，经检定合格；容量瓶，规格为100 mL,经检定合格；移液管，规格为5 mL、10 mL，经检定合格；移液枪，规格为1 000 μL，经检定合格。

2.4 测量原理

采用碱性萃取法萃取样品中的六价铬，通过调节萃取液的pH 值，在酸性条件下加入二苯碳酰二肼，萃取液中的六价铬与二苯碳酰二肼反应生成紫红色络合物，在波长为540 nm处进行定量测定。

2.5 检测程序

样品粉碎后，称取约2.5 g样品，精确至0.000 1 g，放置于萃取皿中，加入50 mL 碱性萃取液、0.4 g 氯化镁、0.5 mL 磷酸盐缓冲溶液。样品溶液在90～95 ℃恒温搅拌3 h，再过滤定容到100 mL 容量瓶中。随同样品做空白试验。

采用浓度为1 000 mg/L 的标准溶液配制5 个浓度的标准溶液。按浓度由低到高的顺序测量系列标准溶液中待测元素汞的光谱发射强度读数，以校准溶液浓度为横坐标、信号强度为纵坐标绘制校准曲线。

校准曲线建立后，测试空白溶液和样品溶液。每个样品独立进行2 次测定。

3 被测量及其数学模型

利用二苯碳酰二肼做显色剂，测定样品中六价铬含量可以归纳为以下模型：

式中，ω为样品中六价铬含量；X为测定的萃取液中六价铬浓度；N为萃取液稀释倍数；V为萃取液定容体积；m为样品称样质量。

4 不确定度主要来源分析

不确定度的主要来源如下（图1）：

图1 不确定度来源分析简化后因果关系

a.本试验中测试样品需要先进行粉碎，然后称取一定的粉碎样品。假设取样的样品是混合均匀的，取样过程对不确定度的贡献在重复性测量中考虑。将各个重复性分量合并为总试验的一个分量进行考虑。

b.称量样品的质量m引入的相对标准不确定度。

c.碱性萃取液定容体积V引入的相对标准不确定度。

d.萃取液中六价铬浓度X测定引入的相对标准不确定度。

e.萃取液未稀释，直接定容到100 mL 容量瓶中作为样品溶液，故萃取液稀释倍数N=1，此处稀释系数无不确定度贡献。

5 测量结果不确定度分量的计算

5.1 样品称量引入的不确定度

由于在不确定度来源分析中考虑将各个重复性分量合并为总试验的一个分量，因此不考虑样品称量的重复性。本试验中由于其称量范围小，天平的灵敏度差异可忽略，因此，不确定度仅限于天平的线性不确定度。

试验采用的电子天平最小分度值为0.000 1 g，按照均匀分布处理，取包含因子k=，天平的线性产生的不确定度分量u(m1)为：

经计算，u(m1)=0.000 058 g。

样品称量中进行称重操作2 次，一次为空盘，一次为毛重，二者可认为是负相关，相关系数取，故天平称量的标准不确定度u(m)为：

经计算，u(m)=0.000 082 g。

样品称量质量m=2.498 8 g，则样品称量的相对标准不确定度urel(m)为：

经计算，urel(m)=0.003 3%。

5.2 萃取液定容体积V引入的相对标准不确定度

定容体积的不确定度主要有3 个方面的来源。一是定容体积重复性引入的不确定度，二是体积校准时的不确定度，三是试验时温度与校准时温度不一致带来的不确定度。

本试验室一般将萃取液定容到100 mL A 级容量瓶中。定容体积重复性引入的不确定度分量合并在总的重复性分量中考虑。

体积校准时的不确定度分量按如下计算。根据JJG 196-2006《常用玻璃量器》可知，20 ℃时，100 mL A 级容量瓶的容量允许误差为±0.10 mL，按三角分布计算，取包含因子k=，由体积校准引入的标准不确定度u1(V)为：

经计算，u1(V)=0.041 mL。

溶液定容时，玻璃容器及其溶液因温度变化会产生体积变化，该定容过程也对不确定度有一定贡献。由于玻璃的膨胀系数很小，在温度变化不大的情况下，玻璃容器的容积改变可以忽略不计。

对于固体和液体，因为其体积膨胀系数很小，为方便计算，在温度不高时体积变化V2为：

在实际试验操作中，实验室的温度波动范围控制为（25±3）℃（置信水平为95%），查得水的体积膨胀系数为2.1×10-4( ℃)-1，按均匀分布计算，取k=，由于试验室温度变化引起溶液体积改变而引入的标准不确定度u2(V)为：

经计算，u2(V)=0.036 mL。

因此，萃取液定容引入的标准不确定度u(V)为：

经计算，u(V)=0.055 mL。

则萃取液定容的相对标准不确定度为urel(V)为：

经计算，urel(V)=0.055%。

5.3 样品溶液浓度测定引入的不确定度

采用紫外分光光度法测定汽车聚合物及电子材料中的六价铬含量，先配制系列标准溶液，根据标准溶液浓度和溶液在特定波长下的吸光度通过最小二乘法线性回归建立回归方程并绘制标准曲线，测定标准溶液之后测定样品溶液及样品空白中的六价铬浓度。

样品溶液浓度测定的不确定度来源主要有3个方面：

a.由标准溶液及其制备过程引入的标准不确定度；

b.由拟合曲线求得试样浓度时引入的标准不确定度；

样品溶液测量重复性引入的不确定度计入总的重复性分量中考察。下面主要对a、b 来源进行分析。

5.3.1 标准溶液引入的不确定度

一是标准物质证书引入的不确定度，查标准物质证书，六价铬标准溶液浓度为100 mg/L，其相对标准不确定度urel(Cr)=0.8%。

二是标准溶液配制过程引入的不确定度，本试验中，分别用浓度为100 mg/L 标准溶液配置5 mg/L 的标准贮备液，然后再取一系列不同体积的5 mg/L 标准储备液定容到100 mL 容量瓶中，得到浓度分别为0 mg/L、0.1 mg/L、0.2 mg/L、0.3 mg/L、0.4 mg/L、0.5 mg/L 的系列标准溶液。

以标准曲线最高点0.5 mg/L 为例，分析由标准溶液配制成标准工作溶液所引入的不确定度。按照JJG 196—2006 常用玻璃量器检定规程[7]，配制0.5 mg/L 标准工作溶液需要使用5 mL A 级移液管1 次、10 mL A 级移液管1 次、100 mL A 级容量瓶2 次。5 mL A 级多标线移液管的容量允差为±0.025 mL，10 mL A 级 多 标 线 移 液 管 的 容 量允差为±0.05 mL，100 mL A 级容量瓶容量允差为±0.10 mL，而且这几个操作不相关，按照三角分布计算，k=，配制标液过程中体积校准的相对标准不确定度ur1(V)为：

式中，ui为第i个量器体积校准所引入的不确定度；Vi为第i个量器的容量允差。

经计算，ur1(V)=0.29%。

由于玻璃的膨胀系数很小，在温度变化不大的情况下，玻璃容器的容积改变可以忽略不计。假设实际操作中，实验室的温度波动范围为±3 ℃（置信水平为95%），20 ℃时水的膨胀系数为2.1×10-4( ℃)-1。则温度差异引起液体体积变化为±V×3×2.1×10-4，按均匀分布计算，取k=，按照B 类不确定评定，配标液时玻璃容器及其溶液因温度变化产生的不确定度ui为：

(2)每天对隧道洞内、地表观测点进行量测，以准确分析滑坡变形的趋势，为变形破坏提供预警，为滑坡治理提供准确的数据。

使用多个容器进行配置标液的合成不确定度u为：

其相对不确定度urel为：

本试验中配制0.5 mg/L 标液用到量体积的容器共4 次，故配0.5 mg/L 标液时玻璃容器及其溶液因温度变化产生的不确定度ur2(V)=0.073%。

由上面计算可知，ur1(V)远大于ur2(V)，且配制溶液过程中时间间隔较短，温度波动较小，故标准溶液配制过程中由于温度变化引入的不确定度分量忽略。因此，配制0.5 mg/L 标液过程中引入的相对标准不确定度即为ur1(V)。

同理，可计算出配置所有浓度标准溶液过程引入的不确定度，如表1 所示。

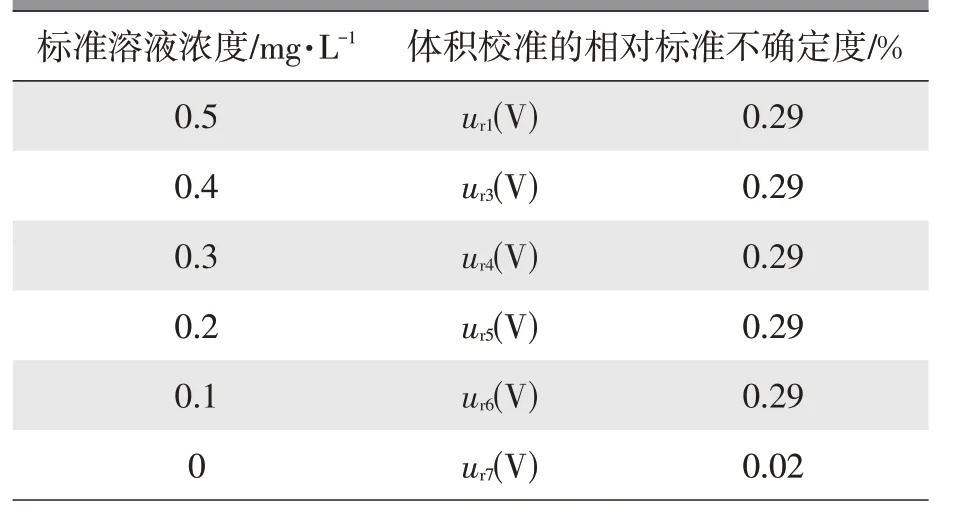
表1 系列标准溶液浓度体积校准的相对标准不确定度

表格中各分量之间相互独立，因此，标准溶液引入的相对标准不确定度urelb为：

经计算，urelb=1.03%。

5.3.2 标准曲线赋值引入的不确定度

此处对于样品溶液浓度测定引入的不确定度考虑采用A 类不确定度评估。

用最小二乘法拟合测定带来的不确定度，得到直线方程A=a+bx，由标准曲线拟合带来的不确定度可由下式表示。

式中，S为按贝塞尔公式求得的拟合曲线的标准差；n为测试标准溶液的总次数，n=12；Aij为第ij个样品测试后从设备上读到的吸光度强度；p为样品重复测定次数，p=2；x0为待测溶液中六价铬浓度平均值0.178 mg/L；xˉ为不同标准溶液测定的平均值；i为第i个标准溶液；j为标准曲线的测定次数。

采用6 个浓度水平的标准溶液，分别重复测定2 次，结果如表2 所示。

表2 六价铬浓度与吸光度对应表

经计算，S=0.003 2，u(x0)=0.003 0，故标准曲线拟合引入的相对标准不确定度ur8为：

经计算，ur8=1.68%。

因此，样品溶液浓度测定引入的相对标准不确定度urel(ρ)为：

经计算，urel(ρ)=1.97%.

5.4 测量重复性引入的不确定度

以拟合的标准曲线为定量标准，对样品进行6次测量，得到样品中六价铬质量浓度数据，测定结果如表3 所示。

表3 样品中六价铬含量测定结果

应用贝塞尔公式计算样品单次测量的标准偏差S为：

经计算，S=0.24。

实际测试时,每个样品测试2 次。故实际测试时,取n=2，样品重复性测量引入的相对标准不确定度urel(x0)为：

经计算，urel(x0)=2.29%。

上表中测定值均为扣除空白后重金属元素的浓度，因为实验室所用试剂纯度较高，空白值很低，对测试结果的影响很小，因此由空白测定引入的不确定度可忽略。

6 相对合成标准不确定度

通过计算，得到紫外比色法测定汽车聚合物及电子材料中六价铬的不确定度各分量如表4所示。

以上不确定的各个分量之间相互独立且不相关，故相对合成不确定度urel计算如下：

经计算，urel=3%。

7 扩展不确定度的评估

将样品质量m=2.498 8 g，定容体积V=100 mL，稀释系数N=1，将数值代入计算模型中公式，得到待测元素六价铬的质量含量如下：

经计算，ω=7.1 mg/kg

取包含因子k=2，得到紫外比色法测定汽车聚合物及电子材料中六价铬含量的扩展不确定度为U为：

经计算，U=0.5 mg/kg。

8 检测结果的报告与表示

紫外比色法测定汽车聚合物及电子材料中六价铬含量结果表示为（7.1±0.5）mg/kg（k=2）。

9 结束语

本文探讨了采用紫外比色法测定汽车材料中六价铬含量的检测方法，通过对试验过程进行解析，深入剖析了测量结果的不确定度影响因素。分析了整个测试过程中不确定度的来源、各种不同来源不确定度的类型及对测试结果起主导作用的主要不确定度影响因素。通过分析表明，测量重复性引入的不确定度分量占比最高，校准曲线拟合的不确定度分量次之，标准溶液配制过程引入的不确定度分量居第3。这3 个是测量结果不确定度的主要贡献者。在实际日常分析工作中，试验人员要特别注意以上因素的影响，规范操作，提高测试的准确性和可信度。