云环境下的仓储物流机器人路径规划方法研究

2023-08-21魏晓晨

机械设计与制造工程 2023年7期

李立,魏晓晨

(1.上海震旦职业学院智能工程学院,上海 201900) (2.山东科技大学机械电子工程学院,山东青岛 266590)

近年来,电子商务业务呈爆炸性增长,随之增加的包裹数量对仓储物流系统的作业效率提出了更高的要求。为适应现代生产需求,物流正朝着智能化方向发展[1]。随着云计算和人工智能等新一代技术与机械设计制造技术的深度融合,智能仓储机器人应运而生,而路径规划就是智能仓储的关键技术[2]。因此,研究基于云计算的路径规划方法具有重要的现实意义。

目前,国内外对仓储物流机器人路径规划方法的研究主要集中在A*算法、动态窗口法、蚁群算法、人工势场法等[3-4]。文献[5]提出一种改进蚁群算法用于仓储机器人路径规划,结果表明,相比于常规路径规划方法,所提方法有效缩短了仓储物流机器人路径长度,且更稳定,具有较强的适应性。文献[6]将人工蜂群和自适应遗传算法相结合用于仓储机器人法的路径规划,结果表明,与常规路径方法相比,所提方法有效降低了能耗,且规划路径更加平滑,更适用于仓储机器人的路径规划。文献[7]提出一种基于线性时序逻辑理论的仓储机器人路径规划,结果表明,与常规A*算法相比,所提方法不仅能够满足复杂的任务要求,而且能够保证路径规划的最优性。文献[8]提出一种改进A*算法用于仓储机器人路径规划,结果表明,相比于常规方法,所提方法有效地缩短了规划时间,得到了最优的规划路径。但上述方法在规划中存在规划路径长和效率低等问题,适应性有待进一步提高。在此基础上,本文结合改进A*算法和改进人工势场法用于仓储机器人的路径规划。其中通过蚁群算法优化A*算法,完成全局路径规划;通过修正势场函数和加入逃逸因子优化人工势场法,完成局部路径调整。

1 基于云计算的路径规划系统

智能仓储物流机器人路径规划需要结合仓储实际环境,本文通过建立环境拓扑模型和路径规划方法确保智能仓储物流机器人安全有效地执行任务[9-10]。智能仓储物流机器人原型采用开放式结构和控制系统,可搭载多种执行器。图1所示为基于云计算网络的智能仓储物流机器人路径规划系统,由云服务器和机器人本体两部分组成。云服务器主要功能是规划实际场景内仓储物流机器人的运行路径和显示实时数据。机器人由主控器、作业部分和行走部分组成。本文基于开源Hadoop框架,通过云计算解决大规模环境中的路径规划问题。

图1 系统结构

2 混合路径规划方法

本文以最小化所有机器人运行总时间为目标函数,通过蚁群算法对A*算法进行优化,完成全局路径规划。但在实际行进中会存在各种障碍物,因此引入改进的人工势场法,完成局部路径调整。

2.1 目标函数

仓储物流机器人路径规划最终目标是找到一条无障碍路径,因为机器人以匀速行走,所以用时最少即路径最短。目标函数如式(1)所示:

(1)

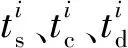
1)一个任务只有一台机器人完成,如式(2)所示。

(2)

2)在当前节点下执行任务mq的机器人时间不能位于之前执行任务mb的机器人保留时间窗中,避免路径发生冲突。如式(3)所示。

(3)

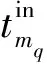
2.2 全局规划方法

A*算法通过启发式函数估计路径代价,选择最低的代价节点作为下一扩展点。代价函数如式(4)所示:

f(n)=g(n)+h(n)

(4)

式中:f(n)为搜索节点的代价函数,g(n)为实际代价,h(n)为评估代价。

站在企业发展的角度上看，企业资金是实现一切运行发展的重要基础前提，只有确保资金充足，才能为企业创造更多的机遇，进而推进企业规模的不断扩大。由此，当代企业在实施资金管理的过程中，必须健全相关绩效考核体系，以此实现对工作人员积极性的有效调动。在实施绩效考评体系的同时，加强对资源消耗的考核力度，深入分析资金的使用是否存在合理性。与此同时，通过不断完善绩效考评体系，实现对资金管理的有效完善。

在A*算法中有两个列表(打开和关闭)。未访问的节点在打开列表中,已访问的节点则在关闭列表中。

A*算法虽然简单,便于操作,但存在路径长、折线多、平滑性不足的问题,不适合轮式机器人的实际应用需要。针对上述问题,进行了启发式函数优化和蚁群算法结合两个方面的改进。

A*算法启发式函数的改进如式(5)所示。

f(n)=g(n)+(1+d/D)h(n)

(5)

式中:d和D分别为机器人的当前位置和从起点位置到目标点的距离。

为了提高A*算法的性能,本文通过蚁群算法对其进行优化,蚁群算法在本质上是一种启发式全局优化算法,可以使改进后A*算法规划的全局路径长度更短、更加平滑。

2.3 局部规划方法

人工势场法使用虚拟力场移动机器人,局部路径实时性好,路径更平滑。基本原理是通过虚拟势场,机器人在力的作用下运动。如图2所示,障碍物对机器人施加排斥力,目标点对机器人施加吸引力,机器人在这些作用力下移动。

图2 人工势场法简图

机器人在空间中的坐标和目标点的坐标分别为Xg=[xg,yg]T和X=[x,y]T,机器人受力如

式(6)所示:

Fh=Fa(x)+Fr(x)=

(6)

式中:Fh、Fa、Fr分别为机器人所受合力、吸引力和排斥力;ρ为机器人与障碍物的相对距离,ρ=|Xg-X|;ρ0为斥力场的作用范围;k1、η为增益系数。

理论上,整个空间势场的最小值点是目标点,但在障碍物分布复杂的区域,因机器人受到的合力为0而无法识别,势场下降到最小点。在实际应用中,拥挤的障碍物会改变机器人移动时施加在机器人上的力,导致路径振动、摇晃或无法向前移动。本文从势场修正和引入逃逸因子两个方面进行优化。

斥力势场修正函数如式(7)所示:

(7)

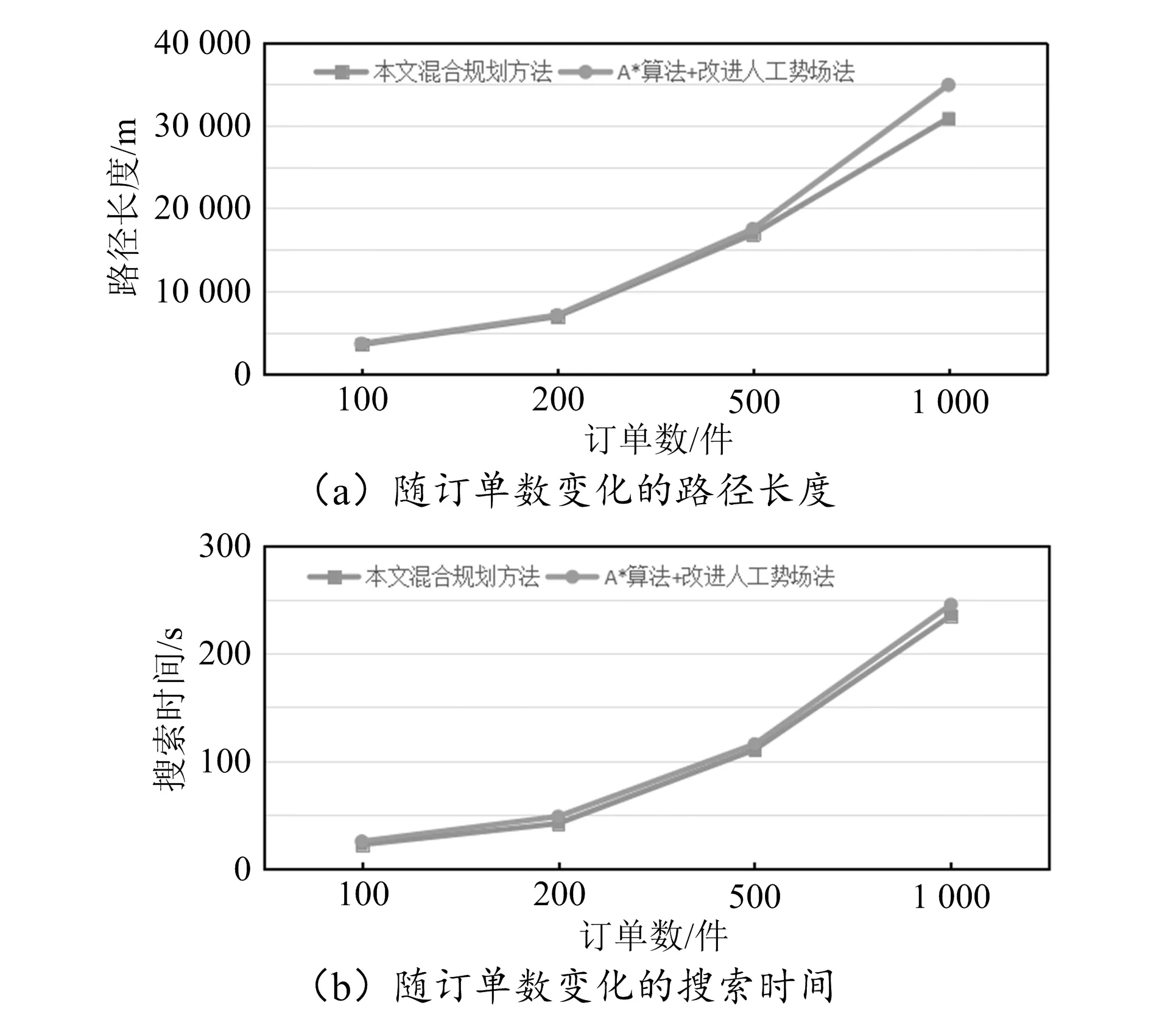
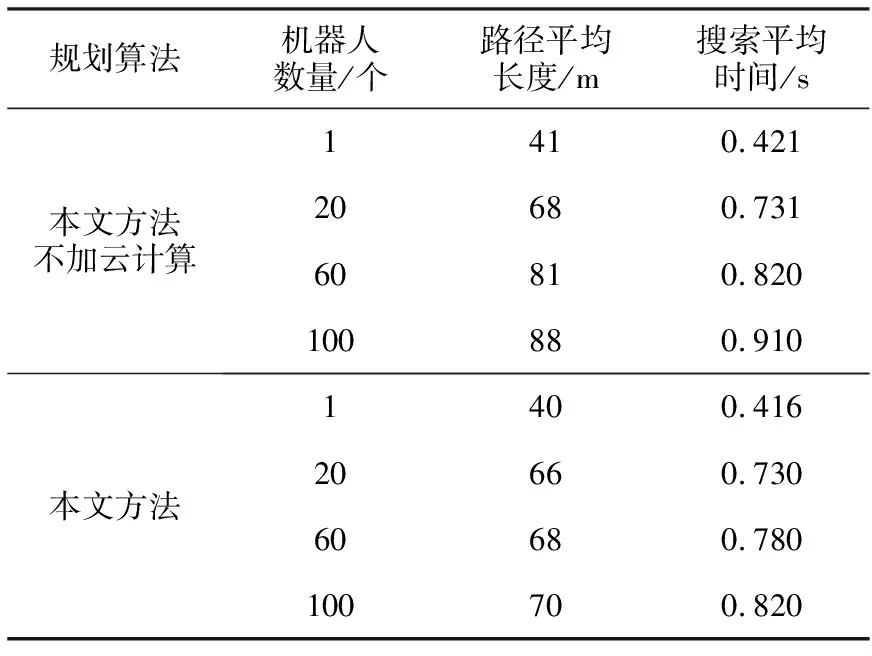
式中:Urg为修正后斥力势场,m为实数(0

机器人所受斥力如式(8)所示:

(8)

式中:Fr1和Fr2分别为Fr的斥力和引力分力。

为了使轮式机器人脱离局部最小值到达目标点,引入逃逸力,逃逸力如式(9)所示:

(9)

式中:Fesc为逃逸力的大小,方向指向目标点,确保其在陷入局部最小值后,合力方向指向目标位置;a、λ1和λ2为正比例系数;a0为障碍物的影响范围;aobs为局部最小值,即距离机器人最近的障碍物距离。为了将逃逸力控制在合理的范围内,在引力方向上添加角度偏移量+mπ/2。

3 结果与分析

3.1 试验参数

为了验证算法的可行性和优越性,通过试验对全局优化算法和混合优化算法性能进行分析。试验在Linux下搭建的Hadoop实验平台上进行。测试环境为10台联想PC机(Intel i52450m CPU、2.5 GHz主频,8 GB内存,512 GB硬盘)组成的集群系统。为了保证结果的精度,结果均为10次运行平均值。在100 m×100 m的仓储环境进行仿真,试验参数见表1。

表1 试验参数

3.2 试验分析

为了验证全局规划方法的优越性,对文中改进的A*算法与A*算法进行了比较分析。设置随机订单数分别为100、200、500、1 000,物流机器人数为1。不同方法全局规划随订单数变化的路径长度和搜索时间结果曲线如图3所示。

图3 全局规划方法结果曲线

由图3可以看出,随着订单数量越来越大,需求越来越高,改进A*算法的路径总长和运行时间均优于A*算法,当订单数量为1 000时,改进前后的路径总长度和运行时间差异达到最大,与改进前相比,优化后分别降低了11.28%和12.37%。这时因为只有1台物流机器人,改进A*算法基于云计算的分布式计算优势无法充分体现。

用本文所提方法从全局算法得到的关键网格节点序列生成全局最优路径节点,并加入改进的人工势场法进行局部路径的调整。将本文混合路径规划方法与A*算法+改进人工势场法进行比较分析,设置随机订单数分别为100、200、500、1 000,物流机器人数为1,不同方法的混合规划结果曲线如图4所示。

图4 混合路径规划方法结果曲线

由图4可以看出,本文的混合路径规划方法随着订单数量的增加,路径长度和搜索时间均优于A*算法+改进人工势场法。订单数量越多,两种方法差异越大,订单数量为1 000时,与改进前相比,本文混合计划方法在路径长度和搜索时间上分别降低了13.05%和10.49%。虽然混合路径规划方法相比于全局规划方法运行时间长了很多,但是混合规划方法可以降低路径长度并提高平滑度。证明混合规划方法是合理和有效的。

为了进一步验证云计算平台对大规模物流机器人路径规划问题的影响,对本文所提方法与基于云计算平台的改进A*算法+改进人工势场法进行了比较分析。选择机器人数为1、20、60、100,对于每个机器人运行10次,采用随机方法,生成机器人的起点和终点,取10次的均值。根据机器人数量的不同,不同混合规划方法运行结果见表2。

表2 不同混合规划方法随机器人数量变化的运行结果

由表4可知,在机器人数量小于20的情况下,本文方法与不加云计算的混合路径规划方法的性能相差不大。当机器人数量超过20时,本文方法与不加云计算的混合路径规划方法相比在路径平均长度和搜索平均时间方面的优势越来越明显,当机器人数量为100时,路径平均长度和搜索平均时间分别降低了25.71%和8.54%。这表明,在大规模应用机器人时,运用分布式计算的云计算平台可以提高本文混合路径规划方法的执行效率,降低规划路径长度,具有一定的应用价值。