GMC2000A加工中心热误差建模方法研究

李有堂,汤雷武,黄 华,吴荣荣

(兰州理工大学机电工程学院,甘肃 兰州 730050)

加工中心在加工过程中产生的误差严重影响了加工精度。随着机床结构的日益改进,热误差成为加工中心最大的误差源,最高达到总误差的70%[1]。因此,减小热误差是提高加工中心精度的首选路径。

热误差是由机床不同构件热效应耦合作用产生的热变形,由于各构件的结构、尺寸以及材料不同,导致构件有不同的热容量、热膨胀系数、导热系数。热变形具有非线性和时滞性等特性,使目前许多热误差建模方法(如经验公式法、数值计算法)存在时滞性、精度不高且外插值性不良等缺点。误差补偿法是软件补偿法的一种,通过对误差源的测量分析,利用数学方法或数学工具对数据进行计算,找出误差源之间的关系,从而建立误差预测的数学模型[2-3]。可以看出,采用误差补偿法对数控机床热误差进行补偿是一个减少成本、提高预测精度且缩短计算时间的优选方法。

在误差补偿法中,BP神经网络建模法具有很强的非线性映射能力和柔性网络结构等优点,许多学者都引用BP神经网络解决数控机床热误差建模问题。Guo等[4]建立了基于蚁群算法和人工鱼群算法优化BP神经网络的热误差预测模型,取得了不错的预测效果,但是BP神经网络未知参数只是进行了随机取值;Huang等[5]引入了遗传算法优化BP网络的初始权重和阈值,发现优化后的BP神经网络可以有效避免陷入局部最优的缺陷,且能够提高预测精度;Li等[6]利用改进的粒子群算法优化了BP神经网络的初始权值和阈值,虽然取得了不错的预测效果,然而并没有对BP神经网络隐含层神经元个数进行优化取值。

从前人的研究中可以知道,BP神经网络存在结构难以确定、容易过学习、易陷入局部极值且泛化能力较差等缺点,如果BP神经网络结构、初始权值与阈值选择不好,网络将会难以收敛,进而不能达到理想的预测效果。萤火虫算法具有自适应全局优化的搜索能力,基于此,本文提出采用萤火虫算法优化BP神经网络,目的是通过萤火虫算法得到更好的网络结构、初始权值和阈值。基本思想是用萤火虫个体位置向量代表网络的隐含层神经元个数或初始权值与阈值,以个体值初始化的BP神经网络的预测值与期望值之间的正则化均方根误差作为该个体的适应度值,通过萤火虫算法寻找最优个体,即最优BP神经网络隐含层神经元个数或初始权值与阈值向量,从而构建萤火虫算法优化BP神经网络模型(firefly algorithm to optimize the BP neural network,FABPNN)。在此基础上建立了FA-BP神经网络热误差模型,并对机床热误差进行预测。最后与BP神经网络和最小二乘支持向

量机模型(least square support vector machine,LS-SVM)进行对比。结果表明,相比于BP神经网络和LS-SVM模型,该方法提高了机床热误差预测效率,且精度完全满足要求。

1 热误差实验及误差数据处理

1.1 GMC2000A机床Y轴热误差实验

误差测量实验在实验室稳定环境中进行,实验安排如下:通过对GMC2000A机床结构的深入分析,选取的关键热源点有电机板(T1)、光栅尺(T2)、十字滑座左(T3)、横梁(T4)、十字滑座右(T5)、电机外壳(T6)、滑块(T7)、环境(T8) 和螺母座(T9)共9个位置。测量方法是:在GMC2000A机床关键热源位置处共布置9个温度传感器(PT100 铂电阻温度传感器),用于测量9个关键点处的温度值,采用激光干涉仪(XL-80)测量和无纸记录仪(XSR90记录仪)记录Y轴定位误差。测量过程中,Y轴总行程为3 400 mm,前后各预留200 mm余量,共3 800 mm,每当Y轴伸进170 mm时,停留5 s,Y轴一个行程约为3 min。为突出温度变化对误差模型的影响,计划Y轴每隔5个行程测量一组数据,每间隔20 min记录一组定位误差数据,共记录840个误差数据,40组温度数据(因为机床运行中温度值变化较小,因此每行程只采集一组温度值)。测量期间,机床的速度设定为6～12 m/min,误差数据如图1所示。

1.2 温度数据的筛选

1.2.1模糊C-均值聚类算法基本原理

在数控机床热误差预测模型中,温度敏感点的数量不同,对模型精度的影响不同[7]。选取的温度敏感点数过多会使得相近测点的输出信号存在多元共线性;过少的温度敏感点数不足以全面反映影响机床热误差的因素,进而导致模型精度不足。为了达到从众多温度测点中选出适当数目测点的目的,在保证信息系统区分能力不变的前提下,需要对机床热误差预测的温度测点进行筛选。

模糊C-均值聚类算法(fuzzy C-means algorithm,FCM)是目前使用最广泛的模糊聚类算法之一[8]。在FCM中设被分类对象的集合为X={x1,x2,…,xN},每一个对象xk有n个特性指标,设xk=(x1k,x2k…,xnk),如果要把X分成c类,则它的每个分类结果都对应一个c×N阶的Boolean矩阵U=[μij]c×N,对应的模糊c划分空间Mfc为:

(1)

则目标函数为:

(2)

式中:RcN为域空间;Jm为聚类损失函数;K为聚类中心数;N为样本数;ci为j簇的中心;m为聚类的簇数,又称加权指数;i、j为类标号;μij为样本xi属于j类的隶属度;xj表示第j个样本,x是具有d维特征的一个样本;‖*‖为任意表示距离的度量。

根据Lagrange乘数法函数极值存在条件求解得:

(3)

加工中心热分布数据经过聚类分析计算后,找出每一类中隶属度值μij最大的数据点,该点就是本类的聚类中心,即温度代表点。

1.2.2基于FCM的测温点聚类选择

对FCM参数初始化,设置最大迭代次数为50,隶属度最小变化量为1E-06。加权指数m控制模型在模糊类间的耦合程度,适当的m值能够抑制噪声、控制隶属度函数等,通过多次聚类分析,最终确定模糊权重指数m=1.5。基于此进行了模糊C-均值聚类,温度点聚类结果见表1。

表1 FCM温度筛选结果

1.2.3聚类有效性评价

温度数据经聚类分组后,对聚类结果进行评价。最好的聚类结果为类间关系疏远、类内关系紧密。现依据聚类本质提出聚类结果有效性评价指标,如式(4)所示,分子为类内距离,分母为类间距离,因此评价指标F(c)值越小,聚类效果越优。

(4)

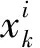
(5)

聚类结果见表2。

表2 聚类有效性指标F值

从表1中可以看到,聚类数为3时,FCM迭代次数最少,且隶属度都大于0.9,分两类和四类时的迭代次数较多,且个别点的隶属度值较小。从表2中可以发现,F(c)最小时分为三类。综上所述,最终确定划分为3类。其中第一类中T8隶属度最大,第二类中T7隶属度最大,第三类中T5隶属度最大,因此确定T5、T7、T8为聚类中心。

2 萤火虫算法优化BP神经网络的数学模型

2.1 萤火虫算法优化BP神经网络模型分析

BP神经网络算法[9]是将输入变量从输入层输入,经隐含层计算后传到输出层并计算得到输出变量,输出变量与实际变量之间的差值进行反向传递,反复修正各网络层间的连接权值与阈值,一直到网络全局误差最小,最终得到BP神经网络模型。

BP神经网络的输入为:

(6)

式中:net为神经网络,xi为样本,ωi为权重因子。

BP神经网络的映射关系为f:Rm→R1,其数学表达式为:

(7)

式中:xi+1为迭代后的样本,cj为隐含层到输出层的连接权值,bj为隐含层节点的输出,ε为输出层的阈值,f(Xi)为激活函数。

(8)

式中:ωij为输入层至隐含层的连接权值,θj为隐含层节点的阈值。

BP神经阈值θj、ε和连接权值ωij、cj可通过训练求得,因此xi+1是可预测的。

但是,BP神经网络存在以下缺点:1)隐含层神经元个数与问题的要求、输入(输出)单元的数目有着直接的关系,隐含层神经元个数太多会使训练时间过长,并且可能出现过拟合现象,隐含层神经元个数太少,无法建立优良的映射关系,使得预测误差变大;2) BP神经网络初始权值和阈值是随机初始化的,导致模型每次预测结果相差甚远;3) BP神经网络的训练容易陷入局部最优。

萤火虫算法(firefly algorithm,FA)是一种智能仿生优化算法[10],其聚类、特征提取等的性能胜过粒子群法、遗传算法等[11-13],因此被越来越多地应用于工程和科学领域解决网络、图像处理等问题[14]。萤火虫在自身的有限感知范围内,会朝着发光更亮的萤火虫(不分雌雄)移动,亮度最高的萤火虫位置就是待定参数的最优解。基于此,本文提出采用萤火虫算法优化BP神经网络,解决BP神经网络存在的诸多问题。

FA寻优过程为:在搜索空间上随机产生萤火虫种群,个体亮度由个体所在空间位置决定,通过比较式(9)可得,萤火虫个体朝着比自身更亮的个体移动;通过计算式(10)得到吸引力值,吸引力极大地影响个体的移动距离;根据式(12)计算移动后的新位置,位置更新公式中增加随机扰动项rand,避免种群陷入局部极值,多次迭代更新后,个体将会移动到最亮个体的位置,即算法得到全局最优极值。

萤火虫i到萤火虫j的欧氏距离rij为:

(9)

式中:d为搜索空间的维度,xi为第i个样本集,xj为第j个样本集,xi,k为第i个样本集中第k个样本,xj,k为第j个样本集中第k个样本。

萤火虫i对萤火虫j的吸引力βij(rij)为:

(10)

式中:β0为最大吸引力,表示光源处(r=0)萤火虫的吸引力,通常β0=1;γ为光强吸收系数,γ的取值影响FA算法的收敛速度和优化效果。

萤火虫i相对与萤火虫j的亮度Iij(rij)为:

(11)

式中:Ii为萤火虫i的绝对亮度,对应萤火虫i所处位置的目标函数值。

萤火虫j被萤火虫i吸引时,j会向i移动,更新原来的位置,j的位置更新公式为:

xj(t+1)=xj(t)+βij(rij)(xi(t)-xj(t))+α(rand-1/2)

(12)

式中:t为迭代次数;xj(t+ 1)为萤火虫j在第(t+1)次迭代的位置;α为常数,α∈[0,1];rand是在[0,1]上服从均匀分布的随机因子。

FA有以下优点:1) 是群体智能算法,它具有群体智能算法的所有优点;2) 受限于吸引度,吸引度会随着距离增加而减小,因此若萤火虫之间的距离较远,较暗的萤火虫不会被较亮的萤火虫吸引过去,这使得整个种群可以自动划分为多个子种群,每个子种群可以围绕每个局部最优,然后在局部最优解中找到全局最优解;3) 如果种群规模比局部最优解多,这种划分会使萤火虫能够同时寻找到所有极值;4)没有遗传算法中的交叉和变异复杂操作,也没有二进制编码;5) 无需设置粒子群算法中的粒子移动速度,无需多次计算概率平均值。因此,本文采用萤火虫算法对BP神经网络的初始权值、阈值和隐含层神经元个数进行优化,建立神经网络效能评估模型,对数控机床热误差进行预测。

2.2 萤火虫算法优化BP神经网络误差模型

萤火虫算法优化BP(FA-BP)神经网络的核心思想为:采用萤火虫种群的迭代优化代替BP神经网络算法输出误差的梯度修正,将隐含层神经元个数或初始权值和阈值编码成萤火虫个体的位置向量,通过不同的萤火虫位置参数训练BP神经网络,使得误差最小,当满足输出精度要求或者达到迭代次数时获得最优解,最后对BP神经网络未知参数进行赋值训练。萤火虫算法优化BP神经网络流程如图2所示。

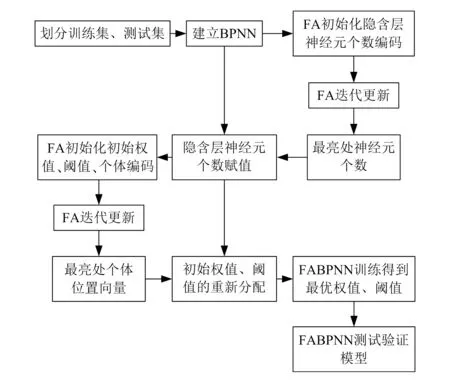
图2 FA-BP神经网络流程

3 GMC2000A机床热误差建模和预测

数控机床热误差建模问题是一个多元函数回归问题,利用FA-BP神经网络解决机床热误差问题是一种简便且高效的方法。通过与BP神经网络和最小二乘支持向量机(LSSVM)模型预测效果对比,验证了基于萤火虫算法优化BP神经网络的优越性。具体建模步骤如下:将通过FCM筛选得到的3个温度变量T5、T7和T8作为BP神经网络的输入,记为xi,将Y轴全程的定位误差作为BP神经网络输出,记为yi,设置学习速率为0.01,最大训练次数为100次,训练目标为1.0E-07,构建BP神经网络的热误差预测模型。

训练数据设置:共40组传感器参数,1～40组数据用于训练,15～30组数据用于测试。

1)神经元节点数设计。输入指标为3个温度数据点,输出指标为1个位移数据点,因此输入层有3个神经元,输出层有1个神经元。隐含层设计为[1,15]之间的整数,进行萤火虫算法寻优得出:当隐含层神经元个数为13时,FA-BP预测目标函数值最小,因此确定隐含层神经元个数为13。

2)FA-BP权值、阈值的初始化。通过以上迭代优化,确定网络的拓扑结构为“3-13-1”。随机初始化萤火虫个体位置向量,如图3所示。经过训练评估,选取最优的初始萤火虫位置向量作为BP神经网络的初始权值与阈值。

图3 萤火虫个体位置向量结构

3)模型训练。利用建立好的模型进行训练,得到FA-BP神经网络模型的最优权值与阈值。

4)误差预测。用训练好的误差模型对Y轴定位误差进行预测。

为验证FA-BP神经网络模型的优越性,从机床冷态到热态过程中,对Y轴行至370 mm处的热误差进行预测,共进行16次,将预测后的残差分别与未被优化的BP神经网络和最小二乘支持向量机误差模型的预测残差进行对比。残差效果对比如图4和表3所示。

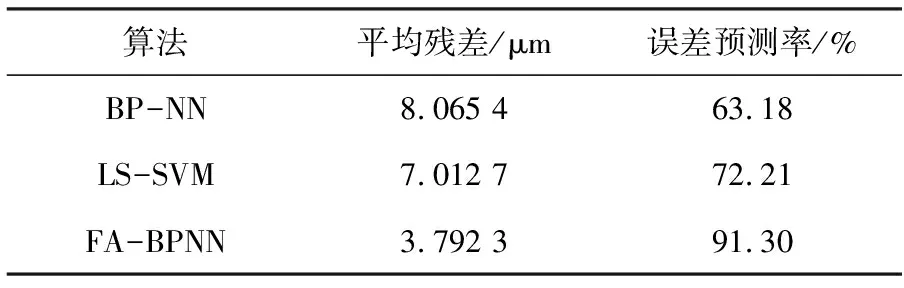
表3 370 mm处多种误差模型预测结果对比

图4 370 mm处多种误差模型残差对比

从图4和表3可以发现,FA-BP神经网络预测效果明显优于未被优化的BP神经网络和LS-SVM,相比BP神经网络,预测精度提高了28.12%,相比LS-SVM,预测精度提高了19.09%。说明对BP神经网络的隐含层神经元个数、权值与阈值进行优化是非常有必要的。

为了对FA-BP神经网络模型全局预测效果进行验证,对机床多个位置进行预测,分别为沿Y轴行至370、1 050、1 730、2 410和3 090 mm处,预测结果如图5所示。

从图5可以看出,机床从冷态到稳态,在Y轴的全部行程中,FA-BP神经网络一直能保持一定的预测精度,进一步说明所建热误差模型预测精度高。

4 温度波动对误差模型的影响分析

在机床误差测量过程中,所有的传感器都有可能受到自身和外界的干扰,导致读取的温度值出现一定的波动。下面将对机床温度数据出现波动时FA-BP神经网络热误差模型的抗扰动能力进行验证。

假设:让每个测点温度分别出现上、下10%的波动,形成两组温度数据,然后误差模型对这种温度波动进行预测,将两种预测结果取平均值,作为温度波动后的最终误差预测结果,最后对误差模型的预测性能做出评价,预测结果如图6所示。

图6 温度波动下FA-BP神经网络全局预测结果

从图6可以看出,当机床温度发生波动时,FA-BP神经网络热误差模型仍然能够保持很好的预测精度。

为了量化误差模型的预测效果,利用真实值与预测值差的均方根误差值RMSE、决定系数R2和预测精度η三个指标进行预测评估,公式如下。

(13)

(14)

(15)

RMSE值是误差模型预测输出曲线和真实误差测量数据曲线间差值的均方根值,RMSE值越接近0,表示误差模型预测越精准。R2值表示误差模型预测输出和真实误差测量数据的相关程度,R2的范围是[0,1],R2值越接近1,表示误差模型的输出越趋近于实测数据。η值描述的是误差模型的性能,η值越高,表示模型预测精度越高。通过计算,萤火虫优化BP神经网络测试是否受温度影响的三个指标参数值见表4。

表4 温度波动预测性能比较

机床在工厂等恶劣的环境下工作,受一些未知因素的影响,往往会导致机床精度下降,这时就需要抗干扰能力强的误差补偿模型,从表4可以看出,均方根值均接近于0,R2值都非常接近1,预测精度η相差较小,且都有很好的预测精度值,这就表示FA-BP热误差模型在恶劣工作环境中仍然能够胜任误差预测的工作。

5 结论

针对热误差影响数控机床加工精度的问题,本文提出了一种结合萤火虫算法与BP神经网络的数控机床热误差建模方法,该方法具有一定的理论研究意义和实际应用价值。第一,为提高模型稳定性和精度,合理布置了机床热传感器,使用FCM算法筛选出具有代表性的热误差参数,构建了无多元共线性的误差数据训练库;第二,为排除局部最小值干扰和加快收敛速度,两次使用FA优化BP神经网络,第一次优化BP神经网络隐含层神经元个数,确定BP神经网络的结构为“3-13-1”,第二次优化BP神经网络初始权值和阈值,避免了BP神经网络采用随机初始化权值和阈值问题。实验验证结果表明,在预测稳定性和精度方面FA-BP模型预测效果明显优于BP神经网络和LS-SVM模型。通过对温度数据添加干扰,验证了模型仍然有很高的预测精度,表明该热误差模型在实际工作环境中抗干扰能力强。