基于HK-RVM 与WCO 的电梯门锁故障预测

郭 俊 李方舟 马凯超

嘉兴市特种设备检验检测院 嘉兴 314000

0 引言

如今随着科技和生活水平的提高，电梯已经成为建筑必备的室内搭乘工具。电梯数量不断地增加，为生活带来便利的同时也导致电梯故障愈来愈频繁，电梯发生故障轻则影响日常生活，重则导致人员伤亡[1]。近年来，基于大数据的研究表明，电梯故障主要包括电梯门失效和电气系统失灵，而电梯门故障大部分是由电梯门触点问题引起的，故及时有效地对电梯门触点进行故障分析和预测十分重要。

Qiu J 等[2]采用了基于MPGA 优化算法的BP 神经网络模型，分析了门锁触点由外力导致故障的问题，对电梯门锁进行故障预测，尽管MPGA-BP 算法能够解决依赖权值随机初始化的问题，但模型收敛速度和训练时间有待提高；Wen P G 等[3]利用PSO-BP 对门锁触点驱动电气装置进行分析，通过分析振动频率对电梯门故障进行模拟预测，PSO-BP 算法解决了学习率对收敛速度以及受节点数影响的问题，但是粒子群算法本身随机性很强，存在依赖初始参数的问题；Zhang A 等[4]利用深卷积森林神经网络算法对人为导致的电梯门故障进行分析预测，深卷积森林神经网络算法在精度、召回率等评估指标上相比于传统算法都有所改进，但与BP 算法一样存在模型收敛速度较慢，计算复杂的问题。

目前，国内外通常利用BP 神经网络算法进行电梯部件的故障分析和预测，但BP 算法存在训练时间复杂、不稳定等缺点。支持向量机（Support Vector Machine，SVM）[5，6]是一种分类效果好、算法简单并兼具高效率性，但也存在无法解决大规模样本问题的算法；相关向量机（Relevance Vector Machine，RVM）[7，8]相比于SVM 引入了贝叶斯算法，能够产生更加稀疏的全局解，预测速度更快，相比于BP 神经网络算法，RVM克服了其缺点并且最优解不存在随参数变化的问题。本文提出的混合核相关向量机（Hybrid Kernel Relevance Vector Machine，HK-RVM）[9-11]是基于RVM 提出的，HK-RVM 采用多核加权方法增加了RVM 的核函数构建混合模型，在先验参数的结构下移除非相关点获得稀疏化模型得到相应最优参数。由于HK-RVM 结合了多个核函数的优点，需要的关联向量更少、概率预测精度更高、泛化能力更强，但存在易受变量控制的劣势。世界杯优化算法（World Cup Optimization，WCO)）是一种通过模拟世界杯各球队之间的相互竞争来确定最优解的数学优化算法，为此，本文利用世界杯算法(WCO)[12，13]对HK-RVM 进行优化，提升了模型的泛化能力和系统的鲁棒性。具体而言，由于接触电阻时间序列信号的变化可以反映电梯门锁是否发生故障，本文首先通过对采集的电阻时序数据进行模型训练，然后利用WCOHK-RVM 模型对电梯门锁触点故障进行预测，获得了电阻大小随时间的变化规律，从而实现对电梯门锁触点的故障预测。

1 理论描述

1.1 混合核相关向量机(HK-RVM)

HK-RVM 采用了多核函数克服了单一核函数的局限性，且是一个高度稀疏的模型，只需少量的样本数据即可获得合理的预测结果，故相比于RVM 预测效果更好。

式中：N为数据样本数量，ωi为模型权重，ε为独立高斯噪声，M(x，xi)为一个非线性核函数。

核函数的选择是模型性能的关键。在众多核函数中，多项式核函数是一种典型的全局核函数，具有很强的泛化能力，高斯核函数是一类具有良好局部学习能力的局部核函数，单纯的RVM 通常采用高斯函数作为核函数导致泛化性和鲁棒性存在局限性。所以本文提出的HKRVM 以单核RVM 为基础，集合了多种不同的核函数，在降低局限性的同时使整个RVM 模型更加全面。混合核函数的具体表达式为

假设目标值yi是独立的，则似然函数可定义为

其中

根据贝叶斯准则和多元条件高斯分布准则，后验分布的表达式为

其中

接下来用极大似然法对超参数α和方差σ2进行估计计算。将新数据x°、预测值y°和方差σ°2定义为

基于1-ζ的置信区间，预测值y°的置信区间的表达式为

式中：Lkζ为预测区间的下限，Ukζ为预测区间的下限，ρζ/2为标准正态分布的双边分位数。

由此可见，HK-RVM 模型预测精度主要取决于核函数参数值，参数值包括m、r、β、δ，接下来将通过优化算法WCO 来对核函数参数值进行优化，从而提高模型的预测精度。

1.2 世界杯优化算法(WCO)

1.2.1 建立大陆与队伍

世界杯优化算法（WCO）是一种基于人类社会智能竞赛的优化算法，WCO 由于其竞争性质和基于最优团队的探索，使WCO 具有不受参数影响、收敛速度快、不易陷入局部极值问题等优点，能够充分地发挥出优化模型的作用。

在搜索空间中形成问题变量的初始值是解决优化问题的一个关键，在WCO 中被称为团队，团队以集群为单位，这些簇被指定为Cn。每个大陆都被设置在搜索空间的不同位置。由于WCO 拥有更多团队，这表明WCO 将得到优化。在这个算法中，投票操作根据排名给最优秀的团队。这一过程一直持续到获得最佳价值的最佳团队，并且大多数团队根据其排名聚集在同一个大陆。

在M个大陆中解决N维优化问题时，设定每个大陆为1×NV(N为变量)的数组来表示各大陆当前参加比赛的球队，数组定义为

式中：xi为某个国家的第i个队伍，所有的变量（x1，x2，…，xNV）都是浮点数，每个大陆的排名通过对变量（x1，x2，…，xNV） 的等级函数的适应度值来实现，表达式为

式中：N为维数，M为大陆的个数。

初始化步骤是该算法的最大优点之一，每个大陆由不同标准差的随机团队的不同值组成。定义的时间间隔被划分为几个大陆，每个大陆在考虑的范围内产生一些不同的随机团队，故该算法的收敛速度比其他算法快得多。

WCO 首先生成大小为Nq×Nv的候选大陆矩阵，其中Nq定义团队的数量，Nv为问题中变量的数量。一些随机组建的团队被认为是针对这些最初的大陆。在最初的国际足联中，有五大陆，每一大陆都包括4 支球队，这些值被用作团队在不同迭代中对每个大陆的投入的初始限制。

1.2.2 团队之间的竞争

在初始化球队后，接下来为评估各大陆的得分情况，得分具有模糊性，因为可能存在某个球队得分过高而忽略掉其他的得分情况，故通过下面的步骤来解决模糊性问题。

1）获取所有的大陆

2）计算各大陆的平均值和标准差，表达式为

3）评分公式为

式中：Ω为排序算子；ψ为标准差效应变化的系数项，ψ∈[0，1]。

4）根据排名在向量中对所有大陆进行排序，假设5 个大陆和n个团队，表达式为

式中：n为每个大陆的团队数量。

在解决得分模糊性问题后，每个大陆的最小值被分离并放入向量变量中用于下一次比赛，XTotal的最小值被选为当前杯的冠军，表达式为

1.2.3 更新

在确定当前杯的冠军后，根据之前的比赛和球队的排名定义新的人口(各大陆及其球队)。这部分不同于真正的国际足联，将采用启发式模式。矢量定义为

式中：Q为大小为N×M的新人口总数，XRd为问题限制区间之间的随机值，XBs为当前最优向量，XBs的特征定义为

式中：α为Ub和Lb之间的精度系数，Ub和Lb分别为所考虑问题的上限与下限。

由于存在交叉点（CP）值的问题，XRd和XBs的大小可以分开并更改为

在产生新的人口后，将被分成n个大陆的m个团队，表达式为

1.3 基于WCO-HK-RVM 模型的电梯门锁故障预测模型

本文采用WCO 算法对HK-RVM 构建的预测模型进行优化，建立WCO-HK-RVM 模型对电梯门锁触点进行预测。技术路线流程如图1 所示。具体步骤为：

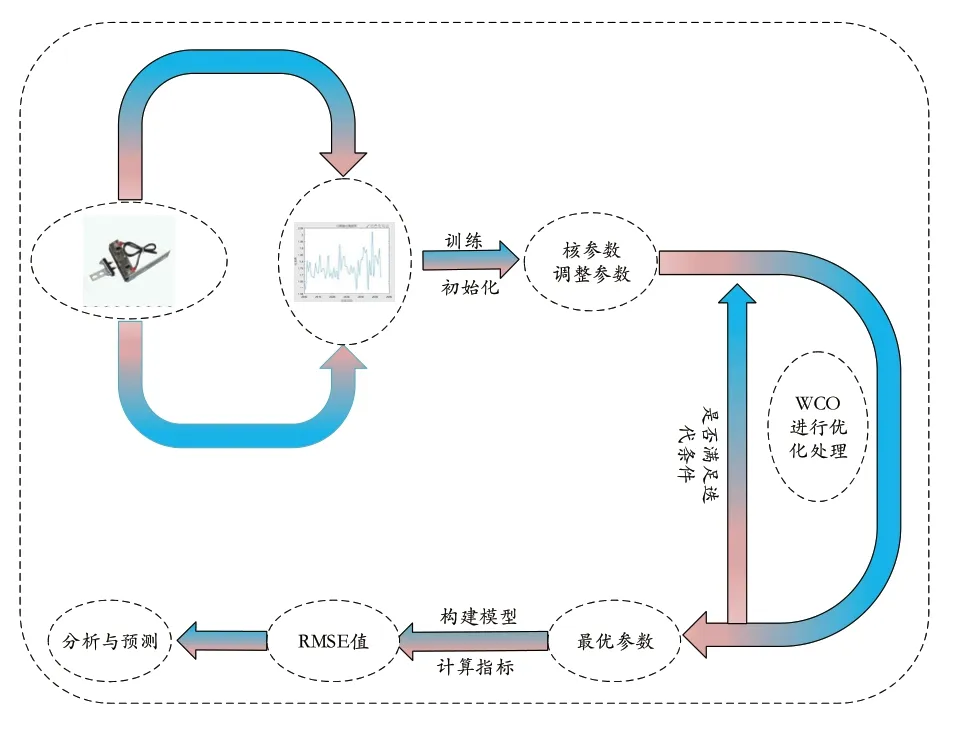
图1 本文所述方法的流程图

1）采集电梯门锁触点数据并进行预处理，生成样本训练数据集和测试数据集。

2）通过训练数据集对HK-RVM 进行核参数、调整函数等参数的初始化。

3）利用WCO 对上述参数进行优化迭代，找到最优参数。即首先设置算法初始参数种群数量及维度；根据公式建立大陆和团队并评估适应度函数值；然后通过解决模糊化问题模型确定团队之间的排名；接下来更新大陆和团队分数，确定下一届参加的大陆和团队，即更新种群的位置；最后重新评估适应度函数值并更新国家和团队分数；判断是否满足迭代条件，若满足则输出排名分数及下一届参加的国家和团队，否则返回步骤3，重新迭代更新计算。

4）通过优化后的最优参数构建WCO-HK-RVM 模型并进行分析，通过评价指标均方根误差(Root Mean Square Error，RMSE)和平均绝对百分比误差(Mean Absolute Percentage Error，MAPE）对电梯门锁触点故障进行分析和预测，分析本文提出的方法的准确率的同时不断地进行优化。

2 实验研究

2.1 数据采集

电梯门锁发生故障会导致门锁电路的电压、电流、环境温度、磁场等发生变化，选取的故障特征必须随故障形式的不同具有不同的表现，故将接触电阻作为故障特征来进行实验分析[14]。为了更好地实现对电梯门锁触点预测，本文采用电动机、控制模块、驱动器和直线移动模组来实现触点的开闭，通过控制模块实现电动机的正反转、驱动器可以调节电动机的实时转速来控制频率、最后利用移动模块实现门锁触点的开闭；利用恒流源、模块CPU、运算放大器和模数转换器等组成的运行电路来实现测试和采集功能，实验模块和测试模块结合采集不同条件下接触电阻实时数据。通过门锁触点模拟模块和单片机测试系统来采集接触电阻数据，并根据数据集绘出电阻时序图，接下来通过模型对采集的55 组数据进行训练和预测，整个实验数据的时序图如图2 所示。

图2 接触电阻时序图

2.2 HK-RVM-WCO 模型预测

为了能够精准反映模型预测的精度，采用RMSE和MAPE 作为评判预测精度的评估指标，表达式为

本文将RMSE 和MAPE 作为WCO-HK-RVM 模型的适应度指标，并对HK-RVM 模型中的核参数、调整参数进行迭代优化从而不断地优化模型，提高模型的预测精度。设定初始参数m=0.9，δ=0.9，β=0.9，设置WCO 最初大陆为5 个，球队数量为25 个。本文将55组数据前50 组作为训练集，后5 组作为测试集。通过计算可以发现训练后模型的RMSE 计算值为0.036 1，MAPE 值为1.252 6，模型预测图为电阻随实验次数变化的规律图像，WCO-HK-RVM 模型的预测结果如图3所示。由图3 可知，本文提出的WCO-HK-RVM 模型预测结果与实际偏离程度更小，基本上达到了完全拟合的状态，重合度较高，能够满足预警和监测的要求。

图3 WCO-HK-RVM 模型预测图

2.3 结果评价

为了能够体现本文提出方法的真实性，采用传统的预测模型SVM 和长短期记忆人工神经网络（Long Short-Term Memory，LSTM）[15，16]对上述数据进行训练，并将计算出的2 种误差与本文提出的方法进行对比。设定LSTM 中神经元个数为200，学习率为0.002；设定SVM 惩罚参数为10，步长为1，核参数设置为0.1，其他均为默认值，SVM 和LSTM 模型预测结果如图4 和图5 所示，RMSE 值和MAPE 值如表1 所示。

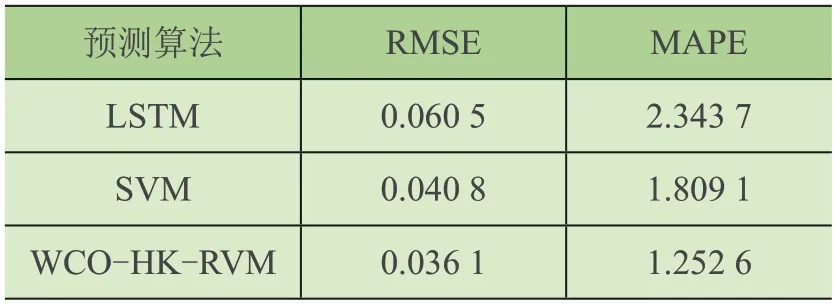
表1 RMSE 和MAPE 对比图

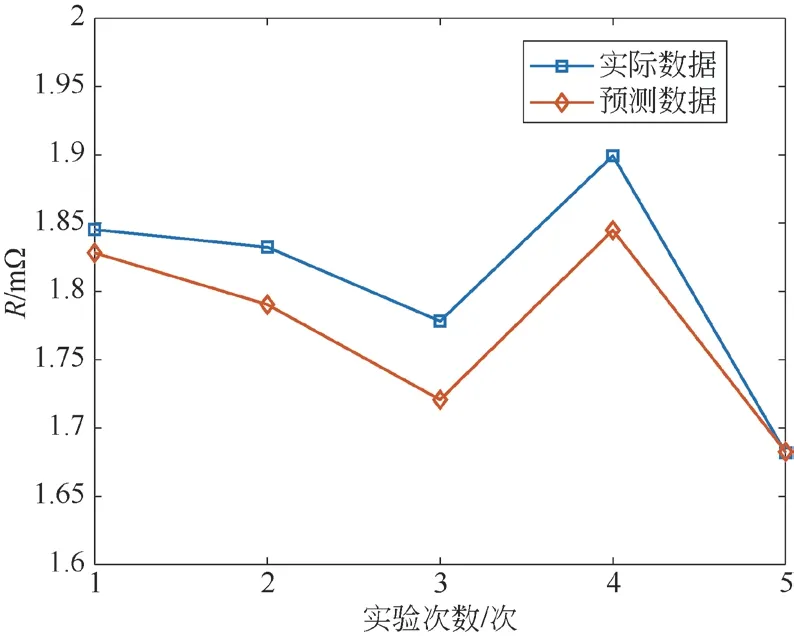
图4 SVM 模型预测图

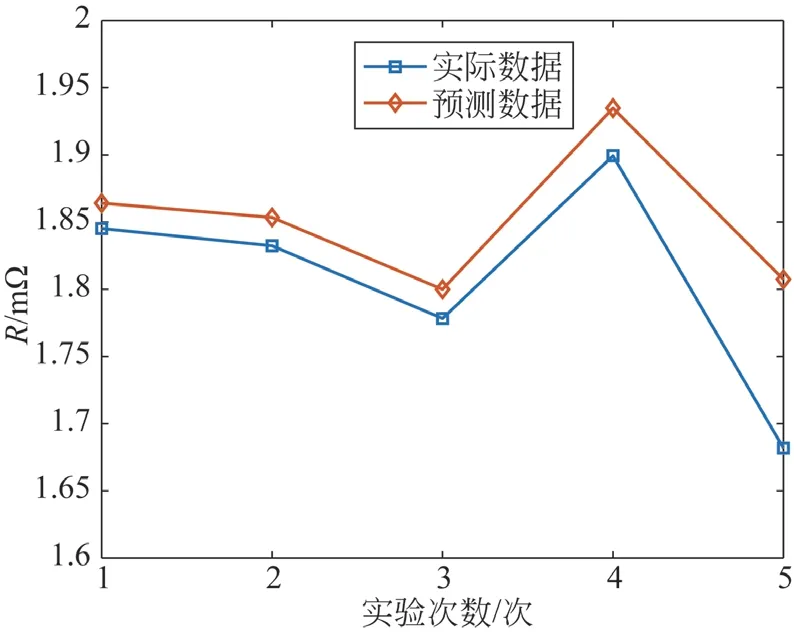
图5 LSTM 模型预测图

由SVM 模型预测的结果可知，实际数据均低于预测数据，正是由于SVM 算法由于核函数选择的随意性会导致预测结果的变化，预测性能和泛化能力下降。由LSTM 模型预测可知，预测结果与实际相近，序列越长LSTM 收敛速度越慢，误差越大，会逐渐偏离实际值导致预测失效，无法完成门锁故障的预警。

通过上面的RMSE 值、MAPE 值和模型预测图对比可知，SVM 预测模型由于过分依赖参数导致存在欠拟合的问题，LSTM 预测模型存在过拟合问题并且随训练次数增加预测效果愈差。本文提出的WCO-HK-RVM相比于传统的2 种方法RMSE 值和MAPE 值更小，误差最低，预测精度更高，收敛性更强。

3 结论

针对电梯门锁触点故障实际问题，在HK-RVM 的基础上，利用WCO 优化算法进行模型优化，提出了基于WCO-HK-RVM 模型的电梯门锁故障预测算法，其具有收敛速度快、预测精度高的特点，可以根据不同的触点故障进行有效的预测。同时，通过采集的电阻时序图数据，并与传统预测算法SVM 和LSTM 相比较，模型的预测精度显著提高，表明该方法可应用于实际电梯故障检测中，在提高生产检测的效率的同时减轻现场人员的工作量。