紧致化智能停车系统的运行冲突控制*

施玉璋 王正国

武汉理工大学交通与物流工程学院 武汉 430000

0 引言

随着社会的发展，近年来我国汽车保有量持续增加，停车难的问题日益显著，高效利用停车资源，使停车系统平稳高效运行已成为当前亟待解决的问题，故紧致化智能停车系统（Smart Compact Automated Parking System，SCAP 系统）应运而生。该系统由移动小车在存储通道上方四向移动以完成车辆的水平运行，减少了传统机械式立体车库水平运行时所需的巷道及移动以腾出空间的时间，有效提高了土地利用率和运行效率。移动小车四向移动容易导致运行冲突发生，影响系统的平稳高效运行。

为解决此类问题，文献[1]提出了动态路径规划的算法框架，为停车系统上多机器人小车的实时并发定义了一个最小障碍物的策略；文献[2]针对智能电梯停车库，在系统中AGV 的最短可行路径上实时更新时间窗以实现无碰撞运行；针对应用广泛的平面移动式立体车库，文献[3]基于全局最优路径使用动态窗口法，预测移动设备在采样速度下将要前进的轨迹和方向，以实现避障运行；文献[4]则给出了不安全状态下基于时间窗算法的RGV 运行冲突控制策略。目前，国内外学者主要通过Petri 网、时间窗迭代和动态窗口法实现存取系统的运行冲突控制[5-10]。

目前，针对停车系统运行冲突控制的研究较少，无法直接迁移至SCAP 系统，且常使用等待或重规划的方法，容易导致系统运行不平稳，且造成较长延迟，影响系统运行效率。本文将结合以往研究，在使用改进A*算法为移动小车规划最佳路径的基础上，提出了时间窗的3 种操作，以速度控制为主，在尽量不影响运行效率的同时实现移动小车的无冲突运行。

1 系统描述

图1 为SCAP 系统的示意图，其存取车操作通过电梯垂直运行车辆，移动小车提升并四向移动水平运行车辆完成，且二者相互独立。

图1 紧致化智能停车系统结构

传统SCAP 系统一般以单移动小车配备于单列存储通道，但容易导致需求与资源不匹配而造成浪费，故引入如图2 的抓取机器人为移动小车，通过前后夹持架、轮胎夹持等实现平面上的四向移动，从而合理调整系统资源配置。此为未来SCAP 系统发展的主要趋势，本文将基于此进行研究分析。

图2 抓取机器人

图3 所示为实现SCAP 系统中多移动小车的无冲突运行，其调度流程为：

图3 移动小车运行调度总流程

Step1：为移动小车规划初始路径；

Step2：预处理阶段，判断并控制移动小车规划路径上的运行冲突；

Step3：实时运行阶段，判断移动小车是否到达终点；若到达，跳转至Step5；

Step4：监测移动小车的实时运行信息，实时控制移动小车运行冲突；

Step5：多移动小车调度结束。

2 移动小车路径规划

2.1 环境建模

规划SCAP 系统中移动小车的初始运行路径，首先需将作业环境信息表示为数字化地图即环境建模。结合移动小车作业环境特点，将基于以下假设使用栅格地图构建环境模型：1）栅格地图的分割单位为存储通道，即1 个栅格点表示1 个存储通道；2）栅格点不表示实际尺寸；3）栅格点以0 和1 分别表示不可/可通行；4）每个栅格点仅可容纳一辆移动小车；5）环境地图中，以白色和黑色分别表示可/不可通行，其余颜色表示在搜寻路径时被访问。

2.2 单移动小车运行路径

2.2.1 基础A*算法

A*算法是由P.E.Hart 等[11]提出的，是静态路网中，一种基于已知路径信息即式(1)向外扩展的典型的最短路径搜索算法，其流程如图4 所示。

图4 A 星算法流程图

式中：f(n)为从起点经由节点n到达终点的路径代价估计值，包含起点到节点n的路径代价实际值g(n)和节点n到终点的启发距离函数h(n)；h(n)为当前节点到终点的实际成本。

2.2.2 改进的A*算法

为移动小车规划最佳初始路径，将从以下几方面改进A*算法：

1）实际意义上路径效果更佳

路径少转向：SCAP 系统中移动小车通过制动后启动实现转向，需长时间占用转向节点，且耗能更多。因此将为扩展节点的启发距离增加转弯惩罚系数tp，以降低转向选择。

路径避免拥堵路段：使用传统A*算法为多任务规划路径时，各节点使用频数不均衡，部分节点高频使用，增加了拥堵和冲突的发生概率。因此，获取并实时更新路径节点n的使用频数即拥堵值c(n)，并根据c(n)增加拥堵惩罚系数cp。

2）搜索效率更高

传统A*算法需耗费大量时间搜寻路径，其f(n)中g(n)和h(n)分别表示Dijkstra 算法的准确性和BSF 的快速性，加入权重比例x以合理分配二者比例，可把握准确性与速度的均衡，提高路径搜索效率。

综上，改进A*算法的f(n)为式(2)；同时考虑运行通道的实际尺寸如式(3)。

2.2.3 路径评价

综合考虑路径运行距离l(n)，拐弯数w(n)，平均拥堵值d(n)及路径搜索时间t以评价路径，并使用minmax 归一化各评价指标为lr(n)、wr(n)、dr(n)和tr，归一化的最值为相同环境下各指标的最值。路径评价函数为

3 运行冲突分析及控制

3.1 运行冲突类型

运行冲突是指移动小车在同一时间争夺同一路径节点从而造成阻塞的情形。由于SCAP 系统中移动小车可四向移动，故运行冲突可分为相向冲突、追及冲突以及节点冲突。相向冲突如图5 所示，指多移动小车相向运行以争夺同一路径节点，可分为交叉相向冲突和对立相向冲突。

图5 相向冲突示意图

追及冲突如图6 所示，指多移动小车在同一运行路径上追及运行以争夺同一路径节点；节点冲突如图7 所示，移动小车的路径节点被障碍物占用，使无法通行，仅在实时运行中发生。

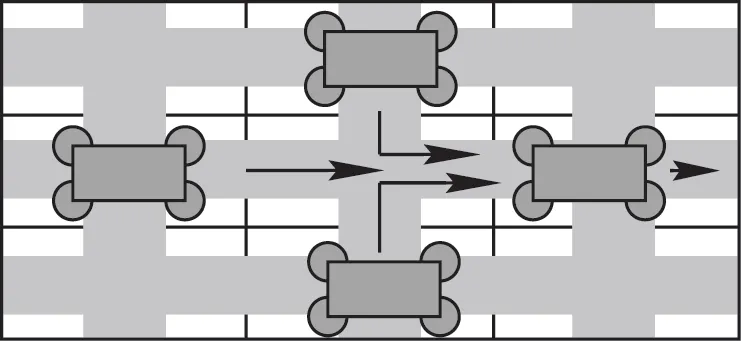
图6 追及冲突示意图

图7 节点冲突示意图

3.2 运行冲突控制

3.2.1 移动小车优先级判定规则

SCAP 系统单层环境中存在多移动小车，按性质可分为存取移动小车、空载移动小车和障碍移动小车。为避免障碍移动小车造成系统局部瘫痪，故其优先级为最高；其次为存取移动小车，最低为空载移动小车。同类移动小车则按下述规则判定优先级：

FCFS（First Come First Serviced）规则：遵循任务发起越早优先级越高的原则；

SRRT（Shortest Remaining Running Time）规则：冲突时的理论剩余行程时间越短优先级越高；

RD（Random Determination）规则：若按上述规则无法判定，则随机确定。

3.2.2 预处理阶段

在预处理阶段，基于冲突时移动小车的优先级判定，提出时间窗的3 种操作，完成移动小车的运行冲突控制。

1）时间窗初始化

时间窗指移动小车从开始进入到开始离开路径节点时所占用的时间段。由初始规划路径NVi＝{ns，…，nm，…，ne}，初始化移动小车Vi的时间窗为WVi＝{wm＝[tmin，tmout]}。ns为路径起点，ne为目标点，WVi为Vi各路径节点的时间窗集合，tmin和tmout为进入和离开nm的时间点。

初始化时间窗应考虑加减速过程。系统运行通道的长度和宽度分别为l和w，通过节点nm时，统一表示直线运行、转弯制动和启动距离为lm、lmb和lma。

①启/制动时节点n1的时间窗为

②加速运行时节点n1的时间窗为

③加速-匀速运行时节点n1的时间窗为

④匀速运行时节点n1的时间窗为

⑤转弯运行时节点n1的时间窗为

由以上计算公式可得到可初始化移动小车在不同运行类型下的节点时间窗，v0和v为进入节点的初始速度和匀速运行速度。

2）时间窗检测

时间窗检测用于判断冲突是否存在及存在类型，通过判断移动小车的时间窗是否重叠，路径NVi是否连续重叠，以及运行方向进行判断。

若时间窗WVi和WVj在节点nm重叠，则表明移动小车Vi和Vj在同一时间点争夺节点nm，判定Vi和Vj存在冲突；若Vi和Vj在冲突节点nm后路径离散重叠，即Vi和Vj在nm处不存在相同或相反的重叠路径，故Vi和Vj存在交叉相向冲突。若连续重叠，且运行方向相反，则Vi和Vj存在对立相向冲突；反之则为追及冲突。

3）时间窗重规划

时间窗检测后，将使用时间窗重规划控制存在的运行冲突。

传统运行冲突主要通过重规划路径或停止等待进行控制，但停止等待下移动小车需不断地启制动，增加了运行能耗，且易导致运行环境的不稳定；而路径重规划则不仅增加启停次数，且会偏离原最佳路线，增加延迟时间。

定义：（Vi，Vj，…，Vm）共n辆移动小车在节点nk处发生冲突；冲突时将移动小车按优先级从高到低排序为0，1…，i，…，（n-1）。优先级i的移动小车为Vpi，Vpi在nk的上一路径节点为，Vpi进入路径节点nk的时间为tpik。

为尽可能减少其余节点的时间窗变化，时间窗重规划将尽量于节点nk-1完成。时间窗重规划包含2 种操作策略：

①策略1（速度调控策略） 指调节Vp(i+1)在节点 的速度变化曲线，使Vp(i+1)到达nk时Vpi已离开，且Vp(i+1)进入和离开节点的速度不变，以避免新冲突的产生。

速度调控策略是基于SCAP 系统中移动小车匀速运行速度v较小，能在较短时间和距离内完成加减速的特点所提出的，如图8 所示，其实质为拉伸Vp(i+1)在的时间窗而避免资源争夺。

图8 速度调控策略下的时间窗重规划示意图

速度调控存在2 种情况。情况1：Vp(i+1)在节点处启动，即为路径起点或转弯点，此时仅需使Vp(i+1)在处等待一段时间后再启动即可；情况2：Vp(i+1)在节点处直线运行，直线运行时Vp(i+1)在处可能存在匀速或加速后匀速运行2 种情况。此时调控Vp(i+1)的速度，使其在上低速运行以拉伸时间窗。当匀速运行时：使Vp(i+1)在处以其加速度a减速至vm，再低速运行时间tm实现等待，最终再加速至v即可，其速度变化曲线如图9a 所示，遵循路程相等原则，速度调控的各参数值需满足式(5)和式(6)，即

图9 速度调控曲线

加速后匀速运行是匀速运行的特殊情况，需使Vp(i+1)以原速度匀速运行时间tm，再提升至速度v即可，其速度变化曲线如图9b。遵循路程相等原则，速度调控的各参数值需满足式(7)和式(8)，即

速度调控策略可控制交叉相向冲突和追及冲突，追及冲突下需使追及移动小车速度小于等于被追及移动小车，以避免新冲突。

②策略2（路径重规划策略） 即速度调控下仍存在少数无法彻底控制的运行冲突，故应使用路径重规划策略，其实质是重规划Vp(i+1)在节点后的时间窗，以避免冲突。

路径重规划即根据当前环境，视冲突节点nk为障碍物，以节点为起点，为Vp(i+1)重新规划至终点的路径，并精简路径以避免“回头路”。

3.2.3 实时处理阶段

在实时处理阶段，移动小车可由自身传感器在节点处检测到冲突现象，此时将在处为移动小车重新规划至终点的路径。极少数情况下若冲突无法解决，则移动小车将紧急制动并发出报警，由人工介入处理。

预处理阶段在很大程度上减少实时运行冲突的发生，经过2 阶段处理，可基本实现SCAP 系统中移动小车稳定高效的安全运行。

4 实验验证分析

4.1 路径规划实验

为验证改进A*算法规划路径的优越性，将在不同环境下实验并由式(4)评估路径。

考虑实际应用规模及发展趋势，以15×15 的SCAP系统运行环境为例，并考虑3 种典型环境，即1）稀疏环境：障碍物较少且稀疏分布，存在于存取频率较低时；2）狭窄环境：障碍物较多，且紧密相连，出现在存取高峰期；3）凹形环境：障碍物较少，但存在U 形分布的障碍物，存在于区域存取频繁时，目前多文献均进行了针对性研究。

各环境下，改进前后A*算法规划的路径及评价如表1 和图10 ～图12，直观表示运行距离为（nx，ny），即沿x轴和y轴经过的节点数。

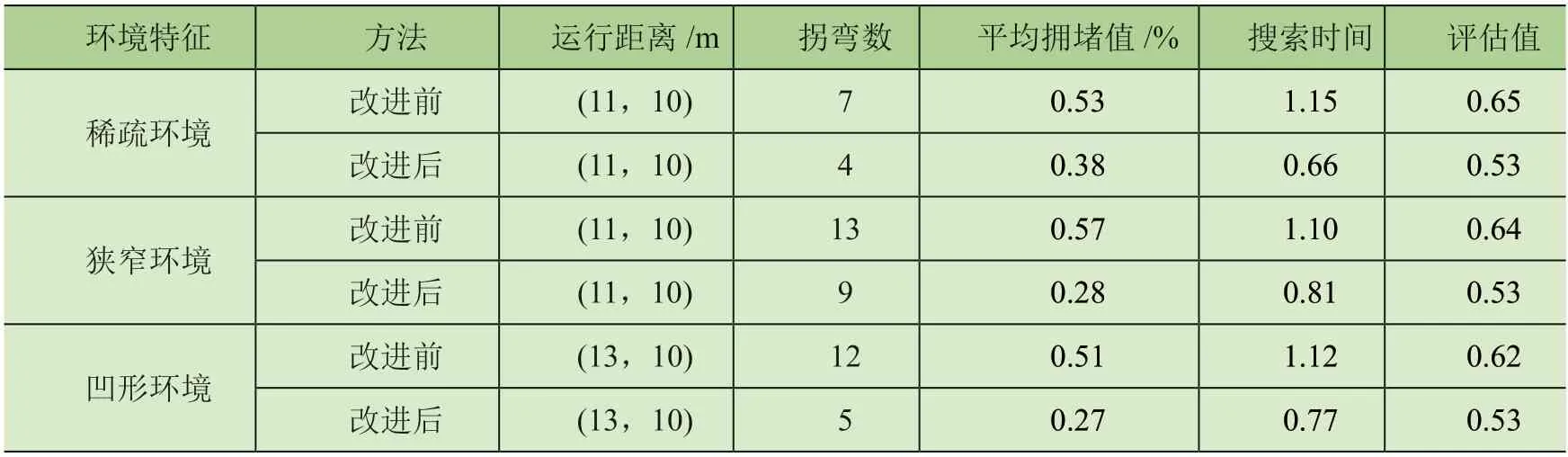
表1 3 种典型环境下路径规划对比

图10 稀疏环境下的路径规划

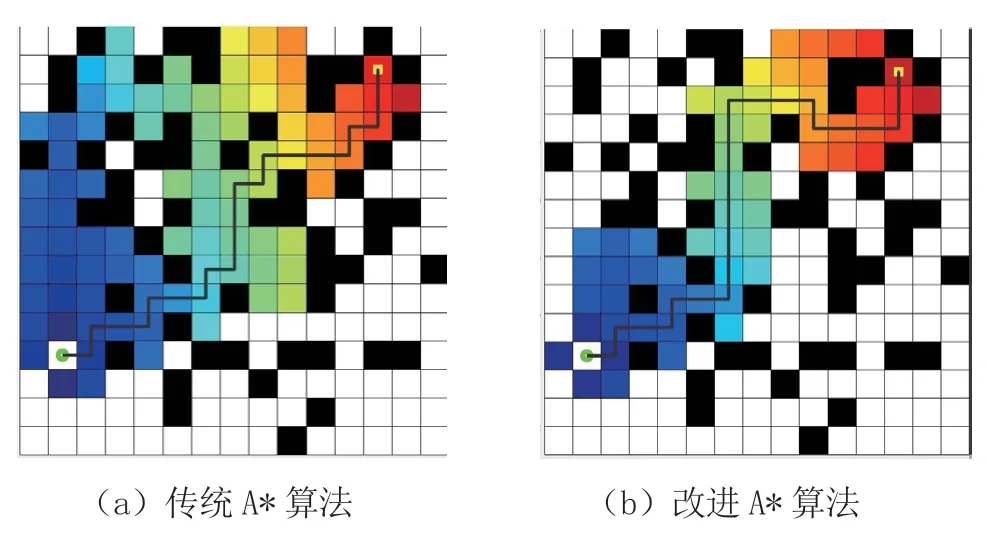
图11 狭窄环境下的路径规划

图12 凹形环境下的路径规划

由表1 和图10 ～图12 可知，在不同环境下，改进前后的A*算法均可为移动小车规划最短路径，但改进后的路径在转向数和节点使用均衡上都有明显提升，且避免了对无用节点的盲目搜索，提高了路径的搜索效率。

以改进前后的A*算法进行相同的多任务路径规划，各节点的使用频数如图13，直观表明改进的A*算法节点使用更均衡，且降低了路径负载峰值，有效减少了运行冲突发生的可能性。

图13 改进前后路径节点负载

综上所述，改进的A*算法能有效提升系统运行效率，减少系统耗能，同时尽可能避免了移动小车运行冲突发生的可能性。

4.2 运行冲突控制实验

4.2.1 有效性验证

基于最佳路径规划，构建运行测试案例如表2 所示；作运行冲突控制实验，实验参数如表3 所示。

表2 运行测试案例

表3 实验运行参数

检测并控制运行冲突，并人为添加节点冲突，可获取运行路径如图14，运行冲突发生级控制情况如表4所示。

表4 测试案例运行冲突发生及控制情况

图14 测试案例运行路径

由图14 和表4 可知，各测试案例均顺利到达运行终点，且速度调控策略下，移动小车的延迟时间较短，路径重规划下延迟时间则与实际运行路径相关。

图15 为冲突2 下节点时间窗示意图，表明了速度调控策略下，移动小车将紧密相连通过冲突节点，节点不存在空闲状态，故延迟时间为不改变运行路径下的最短延迟时间。

图15 冲突2 的时间窗示意图

4.2.2 控制性能分析

运行冲突的控制性能主要表现在延迟时间和启停次数。延迟时间越短，系统运行效率越高；启停次数越多，移动小车启制动更频繁，不仅耗能增大，还容易导致系统运行不稳定。

为表明速度调控策略的优越性，将其与以往研究常用的路径重规划和停止等待进行比较。为避免偶然情况，比较不同方法下多次运行冲突的控制性能如图16，以移动小车5 为例的速度变化曲线如图17。

图16 不同策略下控制性能比较

图17 不同控制策略下的速度变化曲线

结合图16 和图17，速度调控策略的控制性能有显著优越性，其主要原因是在路径重规划下，大多需增加转向以避免冲突，而转向将耗费较长运行时间和增加启停次数；在停止等待时，重新启动需增加延迟时间和启停次数。

在性能比较实验中，存在少数情况下速度调控并非最优，如路径重规划下精简“回头路”，前期冲突控制延迟时间较久而避免了后续冲突等。

综上所述，以速度控制为主的时间窗运行冲突控制能有效完成对运行冲突的检测和控制，且较以往方法有显著优越性。

5 结论

本文基于SCAP 系统对多移动小车调度流程，使用A*算法为移动小车规划初始路径，并提出了移动小车优先级判定下基于时间窗模型的运行冲突控制方法，并通过实验分析了控制方法的有效性和优越性和实际可行性。最终结果表明，本文研究在最短路径基础上，有效控制运行冲突，且较以往方法，该方法能有效提升系统的运行效率，减少系统耗能，有显著的优越性。