基于FLUENT软件的210 t LF精炼炉水冷炉盖漏水原因分析
2023-08-20刘建伟季伟烨
刘建伟,季伟烨
(山东钢铁集团日照有限公司,日照 276800)
包钢(LF)精炼炉作为炼钢工序最重要的炉外精炼方法之一,不管是LF单联工艺路线还是LF+RH双联工艺路线,LF精炼炉对于整个炼钢过程中的成分控制、温度控制、钢水质量以及生产节奏控制都至关重要[1-3]。LF精炼炉的水冷炉盖是精炼炉进行冶炼生产的重要设备,其作用主要是保持炉内还原性气氛[4],促进脱氧、脱硫以及防止二次氧化。此外,水冷炉盖还可对LF精炼炉生产过程中产生的烟尘起到收束作用[5-6]。由于LF精炼炉水冷炉盖下半部分并无耐蚀性材料保护,直接暴露在空气中,因此水冷管壁受到来自钢水以及电极加热过程中产生的热辐射作用极大,这会使水冷炉盖的循环水冷管壁变得脆弱[7]。此外,在生产过程中产生的钢水或钢渣飞溅也会造成水冷管的疲劳强度降低,导致炉盖管路开裂形成炉盖漏水点[8]。这种漏水现象对现场的安全生产、钢水质量、设备作业率以及生产节奏等均产生了很大影响[9]。
当炉盖漏水量较小时,会导致钢水中氢含量的升高[10],对连铸坯的稳定生产和钢板质量控制产生较大影响[11];当漏水量较大时,会引发放炮等恶性安全事故[12-17]。通常情况下,只有在钢水处理结束后,将钢包车开出处理位置再进行检查,才能判断炉盖是否漏水,且在漏水量较小或不漏水的情况下,在钢水处理过程中也可能突然出现管壁大量漏水,因此,LF精炼炉水冷炉盖漏水隐患极大。
在山东钢铁集团日照有限公司投产后,水冷炉盖相继出现了频繁漏水现象,个别新炉盖上线4 d后便开始漏水焊补,漏水频次高的时候能达到2次/班,每次焊补耗时2~6 h,且极易发生焊补处再次漏水或焊补位置周围出现漏水的现象[18],这对生产安全、节奏和质量控制造成不利影响。
笔者使用FLUENT数值模拟软件,对LF精炼炉工艺中钢包底吹氩过程[19]进行了模拟[20-24],从底吹氩气流量、炉渣碱度、渣层厚度和实际炉盖结构等方面,分析了LF精炼炉水冷炉盖漏水的原因,并结合计算结果和现场实际提出了整改措施。
1 LF炉水冷炉盖漏水现场情况
从目前现场实际生产情况来看,LF精炼炉水冷炉盖使用寿命较短[25]。其最根本原因在于,炉盖在使用一段时间后会频繁出现漏水情况,漏水位置如图1所示,图2是水冷炉盖漏水实况。从现场经验来看,炉盖漏水位置主要集中在东西两侧(喂线侧),南北(钢包进出站方向)两侧漏水频次很少。将漏水位置水管解剖后观察发现,管内壁附着大量氧化渣和水垢,见图3。
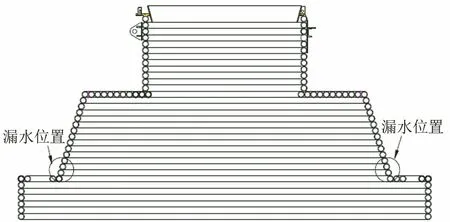
图1 LF精炼炉水冷炉盖漏水位置示意图

图2 炉盖漏水实况

图3 水管内壁杂质
2 数学模拟
2.1 数学模拟基本假设
结合生产现场水冷炉盖漏水位置,使用FLUENT数学模拟计算软件,对钢包底吹氩气时钢包内钢水、钢渣流动的液面波动进行计算。考虑钢水波动具有即时性,使用FLUENT瞬态计算方法,计算钢包内钢水的实时流动情况。
由于钢水在钢包中流动的复杂性,考虑到计算资源不足,且钢包底吹元件对称,因此只取整体的1/2进行计算。并且,为保证计算结果与实际情况吻合,所使用的模型为按实际钢包等比例缩小的模型[26]。
为简化计算,将作出以下假设[27-28]:(1)忽略整个过程中钢包内的化学反应,将密度视为常数;(2)假设吹入模内的气泡是刚性的;(3)忽略温度对气泡的影响;(4)气泡的物性参数为常数。
2.2 计算模型
在计算中为保证结果与实际相符,采用以下模型。
(1) VOF模型[29]
对于VOF模型,相间界面的跟踪是通过求解一个或者多个相的体积分数的连续性方程来实现的,见式(1)。
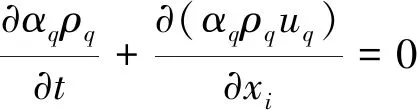
(1)
式中:ρq为第q相的密度,kg·m-3;αq为第q相的体积分数,%,满足公式(2);t为底吹时间,s;μq为相的平均速率,m/s。
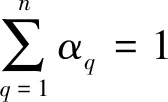
(2)
(2) 动量方程
动量方程见式(3)。
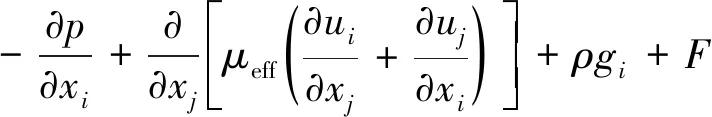
(3)
流体的物性参数根据式(4)~(5)计算。
ρ=αlρl+(1-αl)ρg
(4)
μ=αlμl+(1-αl)μg
(5)
式中:μeff为有效粘性系数,kg·s·m-2;ui、uj为湍流流动的平均速度,m/s;αl为液相体积分数;αg为气相体积分数;ui为流体在x、y、z方向上的速度分量,m/s;ρl为液相流体密度,kg/m3;ρg为气相流体密度,kg/m3;t为时间,s;gi为重力加速度矢量,m/s2;p为流体的压力,Pa;μl为液相流体分子黏度,Pa·s;μg为气相流体分子黏度,Pa·s;F为气体对液体的作用力,N。
(3) 湍流模型
使用k-ε湍流模型(k为湍流动能,ε为耗散率)来描述钢包内钢液的湍流流动,见式(6)~(7)。其中,Pk的值由式(8)决定。
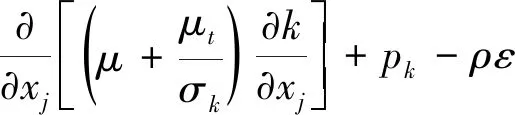
(6)

(7)
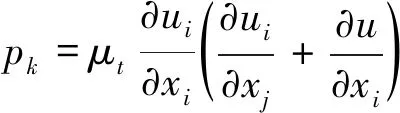
(8)
由k和ε的值可以确定μt,见式(9)。
μt=cμρk2/ε
(9)
式中:k为湍流动能,m2·s-2;ε为湍流动能耗散率,m2·s-2;μ为分子黏度系数,Pa·s;μt为湍流动能黏度系数,Pa·s;ρ为密度,kg·m-3;c1,c2,cμ,σk,σε均为经验常数。
k-ε湍流模型中常数的取值为经验常数,目前普遍采用的经验值为c1=1.44,c2=1.92,cμ=0.09,σk=1.0,σε=1.3。
(4) 离散相模型
使用离散相模型模拟气泡在模内的运动情况,将流体(主要是液相或气相)视为为连续介质,离散相分布于连续相中。使用欧拉法描述连续相,使用Navier-Stokes方程求解速率变量,利用拉格朗日方程描述离散相,因此这种模型属于欧拉-拉格朗日模型。
Fluent软件在拉氏坐标下使用离散相作用力微分方程求解离散相颗粒的轨道,当只考虑主要的作用力时,其方程用式(10)表示。
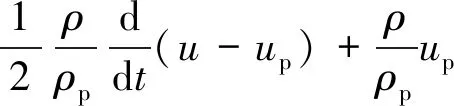
(10)
式中:u为连续相速率,m·s-1;up为气泡速率,m·s-1;ρ为连续相密度,kg·m-3;ρp为气泡密度,kg·m-3;FD为曳力系数。
式(10)所示的等号右边第一项为曳力、第二项为净浮力、第三项为虚拟质量力、第四项为压力梯度。曳力系数FD可按方程(11)计算。

(11)
式中:μl为流体动力黏度,Pa·s;ρp为颗粒密度,kg·m-3;dp为颗粒直径,m;Re为颗粒相对雷诺数,其定义如式(12)所示,系数CD可用式(13)表示。
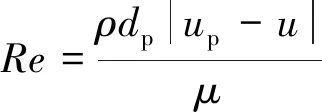
(12)
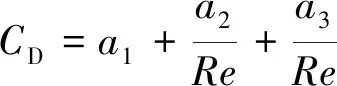
(13)
2.3 计算区域与网格划分
钢包底吹元件位于钢包底部同侧,并沿中轴线对称分布,考虑到液面波动模拟过程的直观性,以及对液面高度的准确描述,按照底吹透气砖的对称原则,取钢包整体的1/2进行计算,网格划分见图4。

图4 计算区域与网格划分
将钢包上部设置为压力出口,底部及侧面设置为墙,设置底吹透气砖为气体入口(如图4所示),中间截面为对称面。
3 结果与讨论
3.1 数学模拟结果验证
使用FLUENT软件计算在大氩气底吹(30 m3·h-3)、高碱度(碱度为7)、薄渣层(200 mm)条件下钢包内钢水液面的波动情况,当t=6 s时钢水液面波动情况见图5。 由图5可见,钢水液面波动较大,液面最高处均为底吹元件一侧,同时图中较为突出的两个峰值分别出现在两侧(图中箭头所示),与实际生产过程中水冷炉盖漏水位置多集中于东西两侧,且靠近与远离底吹元件处各有漏点完全对应。
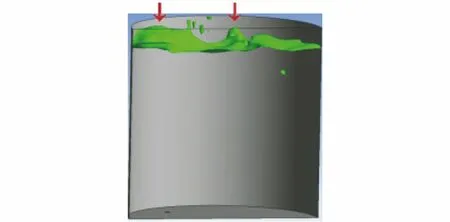
图5 在大氩气底吹、高碱度、薄渣层条件下t=6 s时钢水液面波动情况
3.2 数学模拟结果
在实际生产中,由于冶炼钢种不同,底吹流量、炉渣二元碱度、渣层厚度经常变化。水冷炉盖漏水情况时有发生,为了摸索不同条件下钢包液面流动情况,探索减少因液面波动导致的炉盖漏水方案,设计了4个模拟方案,见表1。

表1 不同条件下钢水液面波动情况模拟方案
3.2.1 方案1下的计算结果
由图6可见:当钢包使用底吹元件进行底吹氩时,随着时间的变化液面波动情况并不相同;随着吹氩时间的增加,钢包内钢水先从底吹元件上方开始出现峰值,随后动能向四周传开,液面开始由底吹元件处向四周波动,并在波动中形成类似于海浪的形态。
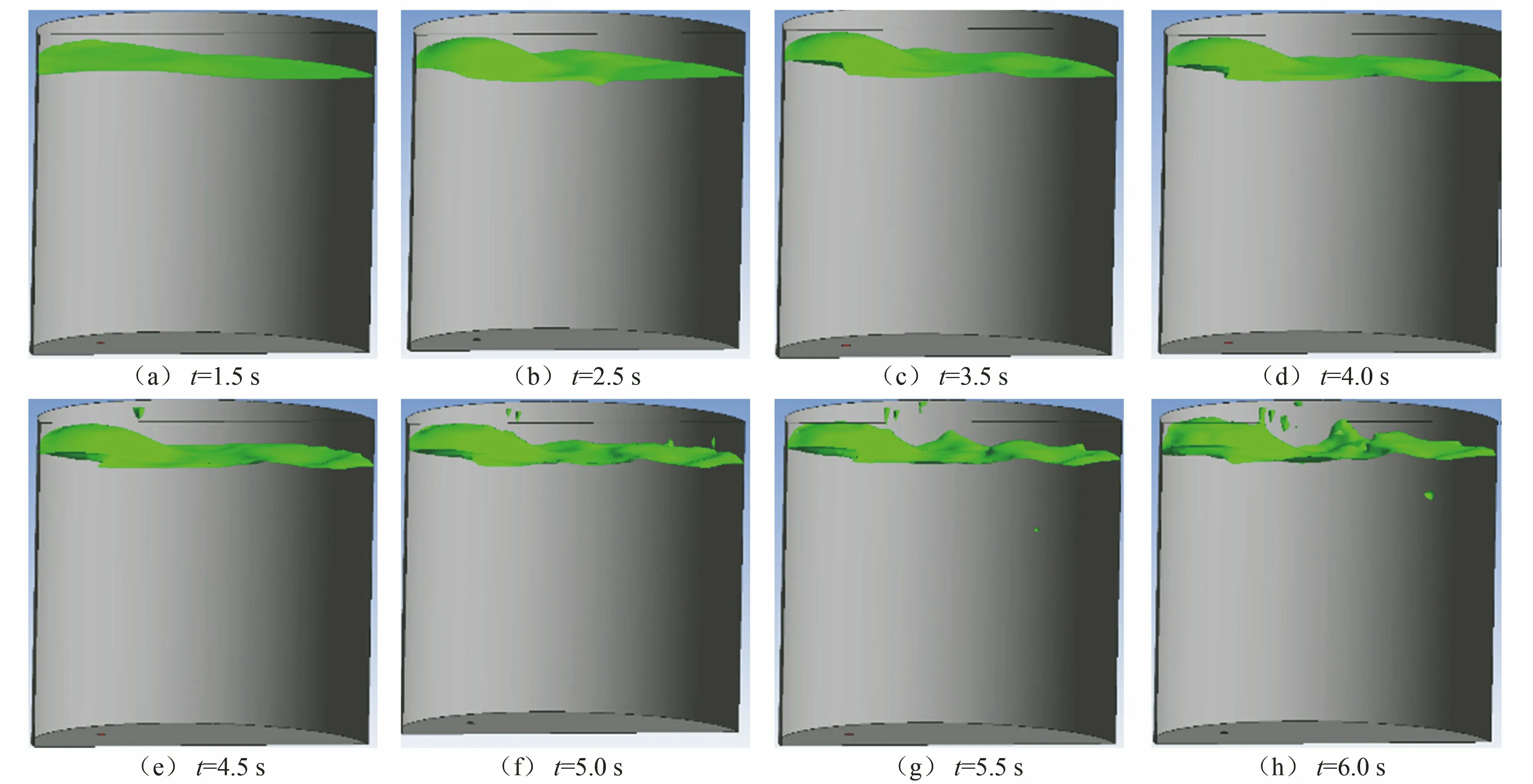
图6 方案1下不同时间钢水液面波动情况模拟结果
由图7可见:当使用底吹氩气搅拌时,由于氩气的提升作用,钢水在底吹元件处向上运动,随后到达钢水液面后产生向四周下落的趋势。因此,在靠近底吹元件一侧,钢水与包壁相互作用产生第一个液面高峰。所对应的钢包原型液面的最高处与包沿的垂直距离约为80 mm,且计算时钢包净空设置为300 mm。因此,当钢包净空<200 mm时,钢水与炉盖距离较小,最高处垂直距离高出包沿约20 mm以上,极易溅射到炉盖上。另外,从图7(a) 可以看出,由于钢包中钢水产生循环流动,钢包南北中轴线两侧形成回旋区。在图7(b) 中,随着钢水不断运动,回旋区不断变化,回旋产生的钢水流股与底吹元件附近下落的钢水流股相互作用,产生第二个钢水液面高峰。

图7 方案1下不同时刻钢水液面速率矢量图
因此,当在LF精炼炉中使用当前底吹元件布置方案时,在大氩气搅拌下钢包中形成两个钢水液面高峰区。当底吹更加剧烈时,钢水液面会在这两处高峰区与炉盖发生碰撞,如果此时加热电极插入过深,会将电极、钢水和水冷炉盖三者连通导电,使得水冷炉盖受到电流作用,引发其薄弱处产生裂纹或者漏点。
3.2.2 方案2下的计算结果
由图8可见:当底吹流量减小时,钢水位于底吹元件上方因底吹气影响产生的凸起明显减小;同时,由于底吹气量小,钢水表面流动不剧烈,在远离底吹元件处仅出现一个高度很低的小凸起;随后在t=4.5 s和t=6.5 s时,钢水液面并无明显变化,流动较为平缓。
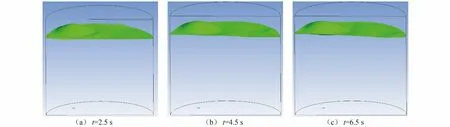
图8 方案2下不同时间钢水液面波动情况模拟结果
由图9可见:由于底吹流量减小,在t=2.5 s时,在远离底吹元件一侧产生的较小的凸起,这是下落的钢水冲击速率较小的回旋区导致的,故此凸起较小;随着时间的不断延长,回旋区速率不断增大,但是增加幅度有限,不足以与大氩气底吹时所产生的速率相比,因此液面晃动的趋势慢慢变小,回旋区趋于稳定。
因此,当使用较小的流量进行底吹氩气时,钢水液面波动显著减小,钢水飞溅到水冷炉盖上的概率也大大减小。
3.2.3 方案3下的计算结果
由图10可见:由于渣层碱度低,因此其与钢水之间的相互作用力减小,故在大氩气流量的底吹条件下,底吹元件上方所产生的钢水液面凸起明显比图4所示的大。图10(a)显示,钢水界面处钢液流速较快,因此在远离底吹元件方向并未产生凸起。随着时间不断延长,产生回旋区的速率显著增大,当t=6 s时,整个回旋区流速较快,同时与底吹元件方向的流股碰撞显著,造成远离底吹元件方向的钢水液面波动剧烈,如图10(b)所示。因此,当使用碱度较低的渣层时,更易产生钢水界面的大范围波动。

图10 方案3下不同时间钢水液面速度矢量图
3.2.4 方案4下的计算结果
由图11可见:当t=2 s时,由于渣层较厚,回旋区钢水与渣层交互作用较大,最初由底吹元件上方向四周下落的钢水与速率较小的回旋区钢水碰撞,在远离底吹元件方向产生较大的凸起;随着时间的不断延长,下落流股在厚渣层的作用下速率逐渐减小,形成了如图11(b)所示的钢水流股速率减小、凸起高度减缓的情况;当t=6 s时,钢水除在底吹元件上方凸起较高外,在靠近包壁的一侧波动较小,并未出现明显的钢水凸起现象,即此时远离底吹元件一侧的钢水飞溅到水冷炉盖上的概率大大降低。

图11 方案4下不同时间钢水液面速率矢量图
3.3 讨论
3.3.1 水冷炉盖的冷却方式
结合不同方案下的计算结果,对炉盖漏水具体部位进行了数据统计。结果发现,出现在高温热辐射区的第1114环冷却水管(见图12)的漏水频次高达90%以上,此处冷却水路设计为一个支路,该支路冷却水由第11环水管进入,出口为上层的第14环水管,与相邻支路比较,处于高温热辐射区的支路冷却强度偏低,回水温度通常都在50 ℃以上,高的时候能达到80 ℃,也说明了冷却能力差的问题,结合图3分析,还存在冷却水汽化的现象。

图12 水冷炉盖高温热辐射区示意图
3.3.2 钢包净空的影响
当钢包净空过小时,在LF精炼炉加热、搅拌过程中,溅起的高温液态钢渣也会附着在水冷炉盖内罩管壁上,尤其是冶炼低硫钢种时,需要大氩气搅拌实现脱硫效率和深度。在大氩气搅拌过程中,氩气对渣层的冲击导致钢渣飞溅并附着在管壁上,过小的钢包净空也会出现溢渣现象,这会增加钢渣在管壁上的附着概率。现场经验表明,当钢包净空<200 mm时,水冷炉盖内罩管壁黏渣的概率与净空大小成反比,尤其当净空<50 mm时,黏渣量非常大,平均黏渣量达到了8 kg·炉-1。同时,当钢包净空过小时,加快了渣线砖的侵蚀速率[30],大大降低了钢包的寿命。
3.4 改进措施
3.4.1 生产工艺及操作改进
为了防止水冷炉盖漏水现象频繁发生,根据计算结果和实际经验,从生产工艺及操作方面提出以下控制措施:(1)钢包净空严格控制在200~450 mm;(2)加热时底吹氩流量控制在0到20 m3·h-1以内;(3)通过添加造渣石灰,控制炉渣碱度在5以上;(4)使用CaC2发泡方法增强埋弧效果。
3.4.2 炉盖冷却结构改进
为了提高水冷炉盖高温热辐射区的冷却效果,结合现有冷却方式,对高温热辐射区的冷却结构进行了改造,将第11~14环水管的一个冷却支路改造成两个冷却支路,即第11~12环水管为一个冷却支路(见图13),第13~14环管为一个冷却支路,两个支路的进水流量与之前的一个支路相当,以此提高高温热辐射区的冷却强度。
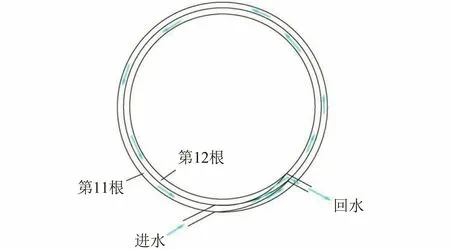
图13 进回水结构示意图
4 结论
(1) 数学模拟计算结果显示,易产生漏点的区域分别是底吹元件附近和远离底吹元件处。靠近底吹元件处的漏点是底吹氩气的提升作用造成的;远离底吹元件处的漏点是氩气从底吹元件处向四周流动时与钢水表面回旋区碰撞形成的。
(2) 大氩气流量造成钢水液面波动剧烈,易产生两处较高的凸起;当渣层碱度较低时,钢水与渣层作用力下降,液面波动剧烈;当渣层厚度较小时,无法对钢水表面产生较好的覆盖作用,钢水波动剧烈。
(3) 在钢包底吹氩过程中,适当减小大氩气流量、提高渣层碱度和厚度,有利于减少水冷炉盖黏钢或黏渣。
(4) 通过现场工艺和操作的实施,以及对水冷炉盖冷却结构的优化改造,炉盖漏水现象得到了根本性遏制,漏水频率由优化前的平均2次/d,到现在炉盖连续使用了10个月未出现一次漏水,这对现场安全稳定生产、降低劳动强度、提高设备作业率、提高产品质量等均起到了积极作用。
