基于高铁全生命周期的县域经济发展——以沪昆高铁为例

尹正,郐浩奇

安徽建筑大学经济与管理学院,安徽 合肥 230022

0 引言

2000年以来,我国以高铁为代表的基础设施建设成果显著,截至2022-12-30,高铁运营里程突破4.2万km,稳居世界第一[1]。高铁快捷舒适,可缩小地区间的时空距离,加速资源禀赋流动,促进沿线地区的经济发展。修建高铁成为经济欠发达地区快速发展经济的重要手段,易引发县与县间的高铁争夺战。产生高铁争夺战的主要原因是未全面、正确认识高铁与县域经济发展的关系。可通过对高铁建设运营全生命周期的理论和实证分析探究高铁对县域经济发展的影响和作用机理,为政府决策提供参考。

国内外学者对高铁的研究分为不同阶段。早期阶段以理论分析为主[2],如高铁开通可加强区域一体化,改变区域空间结构,同步提升各地区的可达性[3],促进区域旅游业发展[4]。第二阶段以早期理论为基础,定量分析高铁效应,如高铁通过影响人口流动促进区域联系[5];高铁网络的逐步完善提高可达性水平,外围地区效果显著强于中心地区[6];促进区域经济增长[7],加强区域间经济增长的溢出效应[8]。现阶段的研究呈多样化,包括高铁开通的显著就业效应、二氧化硫排放降低及流感发病率提高等[9-10]。

对高铁的研究区域集中在地级市层面,县域(县和县级市)较少。以县域为样本可有效降低内生性的干扰:在高铁规划过程中,相比中心城市(省会城市、副省级城市、计划单列市等),县域话语权较小,主要服从上级部门安排,有效减少自选择偏差导致的回归不一致[11];县域发展相对缓慢,资源相对不足,高铁开通易使本地人才和资源流出,形成集聚阴影[12]。研究中对高铁建设期的关注度较低,从高铁项目拟定、可行性评估到施工、运营和维护,时间跨度较长,只分析高铁的运营期易存在遗漏。

本文以县域经济发展面板数据为研究样本,分析高铁全生命周期对县域经济发展的影响范围及作用机理,测定高铁各阶段作用的辐射范围;在稳健性检验中,采取多期固定效应回归与渐进双重差分(difference in differences,DID)相结合的方法进行分析,确保结果的可靠性,以期为政府决策提供参考。

1 研究方案设计

1.1 研究样本

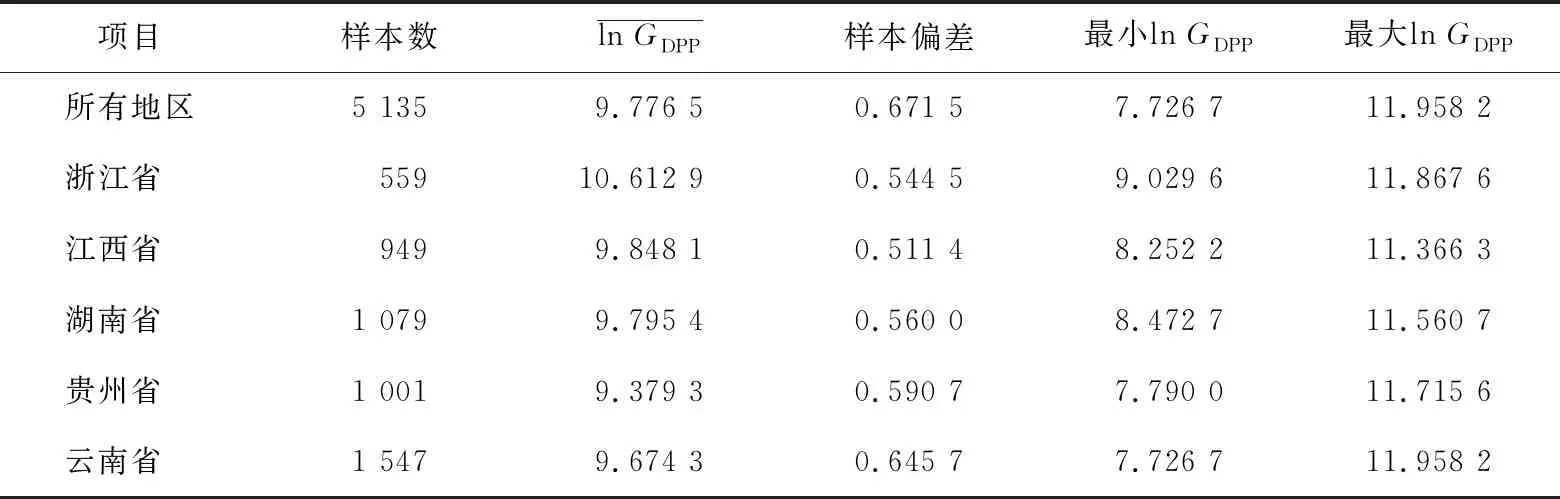
表1 2008—2020年沪昆高铁沿线各省的县域经济分析结果

1.2 影响机制

分别探讨高铁建设期和运营期对县域经济的影响范围和作用机理。

在高铁建设期,建设铁路需大量钢材、水泥、木材和电器等材料,为节省运输成本往往就近取材;建设期耗时长、工程量大,需大量施工人员、管理人员和维护人员,为高铁沿线地区提供大量就业岗位,促进当地经济的发展。高铁建设期主要通过第二产业促进县域经济发展,且集中在高铁沿线一定距离内,超过此范围则未产生明显影响。

在高铁运营期,高铁能提升地区间的可达性,促进地区间的资源禀赋流通,改善劳动资源错配和企业资源错配问题。中心城市凭优势吸引人才、资金和高新产业流入,促进中心城市发展,地区间差距增大[17];中心城市对临近城市产生扩散效应,借助高铁资源快速流动。中心城市发挥扩散和虹吸2种效应,以中心城市为核心,2种效应随地级市与中心城市间距离的改变此消彼长,在较近距离内,以扩散效应为主导,带动邻近地区经济发展;随距离的增大,以虹吸效应为主导,抑制县域经济发展,产生集聚阴影[18]。

因此,提出2点假设:高铁建设期内,沿线县域的经济发展主要通过第二产业得到提升;高铁运营期内,在距中心城市一定范围内开设站点的县域经济发展因人口外流受到抑制。

1.3 研究方法

在政策评估中,将固定效应回归与DID结合可避免遗漏变量问题,应用较广。高铁开通与政策实施类似,但采用DID前需进行平行趋势检验,确保处理组与对照组差分后得到纯效应结果。对用来证明假设的数据进行平行趋势检验,结果如图1所示。横坐标为0表示高铁开通当年,图1上侧和下侧的虚线分别表示处理组与对照组的被解释变量具有相同变化趋势的最大和最小可信度。由图1可知:高铁开通前处理组与对照组的经济发展趋势相同,高铁开通后,二者的经济发展趋势显著不同,符合平行趋势的假设。

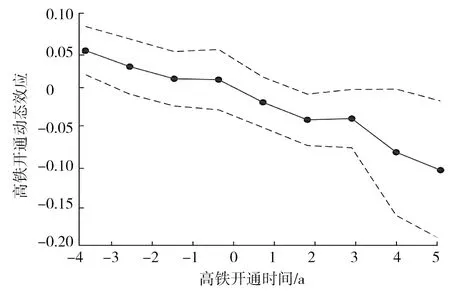
图1 原始数据的平行趋势检验

在高铁建设期,相较于高铁在哪个县域设站,县域是否处于高铁沿线及距高铁线路远近具有更强的随机性,更符合随机分组的条件,因此采用面板固定效应回归的方法进行分析;在高铁运营期,采用多时点DID模型进行分析。

被解释变量为lnGDP,控制变量分别为县人均财政预算支出xf的对数lnxf,县人均贷款余额xloan的对数lnxloan,县人均储蓄存款xsav的对数lnxsav,县人均社会消费品零售额xsale对数lnxsale,人口密度ρpop,各控制变量统计结果如表2所示。由表2可知:各变量分布合理,未出现极端数据。为排除多重共线性导致的回归结果不准确问题,对变量进行相关性检验,结果显示方差膨胀系数均小于10,可排除多重共线性。

表2 各控制变量的统计结果

2 实证与检验

2.1 高铁建设期

2.1.1 高铁建设期基准回归

对高铁建设期进行基准回归,构建被解释变量的模型

Yit=α0+β1Tit+β2Xit+Ci+tyear+εit,

(1)

式中:α0为截距;β1为高铁建设对县域经济的影响系数;Tit为建设期虚拟变量,某县处于高铁建设期内时,Tit=1,反之,Tit=0;β2为控制变量的影响系数;Xit为控制变量;Ci为个体虚拟变量,排除时间固定时县与县间的个体差异;tyear为时间虚拟变量,排除个体固定时时间维度上的差异;εit为误差项。

将2012、2013年设为高铁建设期,期间人均生产总值的对数为lnGDP-3,基于高速公路与高铁线路的高度重合性,为排除高速公路的干扰,引入高速公路虚拟变量后人均生产总值的对数为lnGDP1-3。中心城市以高速公路为依托对周边区域产生辐射,中心城市的扩散效应与建设期福利效应叠加。根据中心城市1 h经济圈发展战略[19],以1 h车程为半径,分别剔除距中心城市40、50、60 km范围内的县域进行回归,回归结果分别为lnGDP2、lnGDP3、lnGDP4,如表3所示。由表3可知:lnGDP-3、lnGDP1-3回归结果显著为正;lnGDP2、lnGDP3、lnGDP4回归结果依然显著,表明高铁建设期带动了相邻县域的经济发展。

表3 高铁建设期各变量的回归结果

2.1.2 高铁建设期福利效应范围

测度高铁建设期的福利效应范围,构建高铁建设期被解释变量的模型

式中Gj为高铁建设期不同的福利效应范围。

将各县域政府与高速铁路的垂直距离按大小排列,剔除极端数据,以5分位数进行分组,根据回归结果对分位数微调,得到最理想的福利效应范围分组G1(0～35.2 km)、G2(>35.2～77.0 km)、G3(>77.0～120.0 km)、G4(>120.0～237.3 km)、G5(>237.3～550.0 km)。福利效应影响下各县人均生产总值的对数为lnGDP-4,排除高速公路干扰后各县人均生产总值的对数为lnGDP1-4。以1 h车程为半径,分别剔除距中心城市40、50、60 km范围内的县域进行回归,回归结果分别为lnGDP2-4、lnGDP3-4、lnGDP4-4,如表4所示。将lnGDP2-4作为最终解释结果。由表4可知:lnGDP-4与lnGDP1-4相近,在G3区域内回归结果显著性开始减小,但在G1、G2内高铁建设期与经济发展始终显著正相关,高铁建设期福利效应随各县域政府与高铁垂直距离的增大而递减。

表4 福利效应范围影响下高铁建设期各变量的回归结果

2.2 高铁运营期

2.2.1 高铁运营期基准回归

对高铁运营期进行基准回归,构建高铁运营期被解释变量的模型

Yit″=α0+β1tit+β2Xit+Ci+tyear+εit,

(2)

式中:tit为高铁运营期的虚拟变量(核心解释变量),tit=treatedtimeit,若某县开通高铁,treated=1,本县为处理组,本县未开通高铁,treated=0,本县为对照组;若某年为高铁开通后的年份,timeit=1,反之timeit=0。若高铁在6月30日前开通,视为当年开通;反之视为次年开通。若tit=1,β1为高铁开通后带来的经济影响系数。

对高铁运营期的设站县进行全样本回归,高铁运营期各县人均生产总值的对数为lnGDP-5,控制高速公路的干扰后高铁运营期各县人均生产总值的对数为lnGDP1-5,控制个体、时间双向固定效应后各县人均生产总值的对数为lnGDP5,为验证结果的稳健性,控制个体、时间双向固定效应并控制高速公路的干扰后高铁运营期各县人均生产总值的对数为lnGDP6,回归结果如表5所示。由表5可知:lnGDP-5、lnGDP1-5、lnGDP5、lnGDP6的全样本回归结果均表明高铁开通对县域经济有抑制作用,但差异明显。lnGDP5回归结果在1%水平下显著,高铁开通使县域人均生产总值减少6.23%。lnGDP6回归结果依然显著为负,县域人均生产总值减少5.57%。

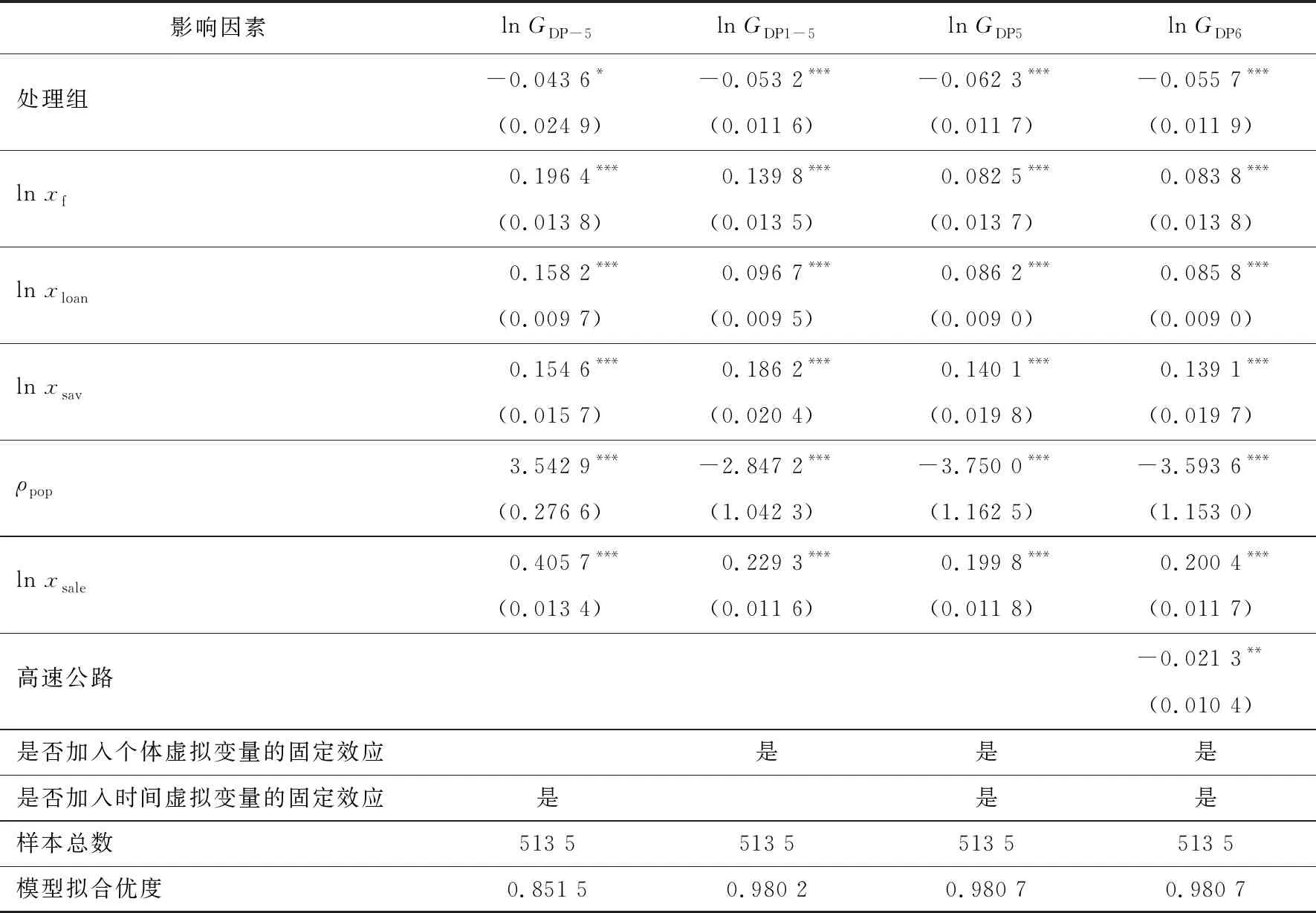
表5 高铁运营期设站县的全样本回归结果

2.2.2 距离分组回归

划分距离后,对高铁运营期进行全样本回归,各县人均生产总值的对数为lnGDP-6,控制高速公路的干扰后高铁运营期各县人均生产总值的对数为lnGDP1-6,控制个体、时间双向固定效应后各县人均生产总值的对数为lnGDP7,为验证结果的稳健性,控制个体、时间双向固定效应并控制高速公路的干扰后高铁运营期各县人均生产总值的对数为lnGDP8,回归结果如表6所示。将lnGDP8作为最终解释结果。由表6可知:Group2～Group5处为阴影区,且高铁开通对县域经济的抑制作用呈∩型特点,在Group4处达到最大抑制作用。

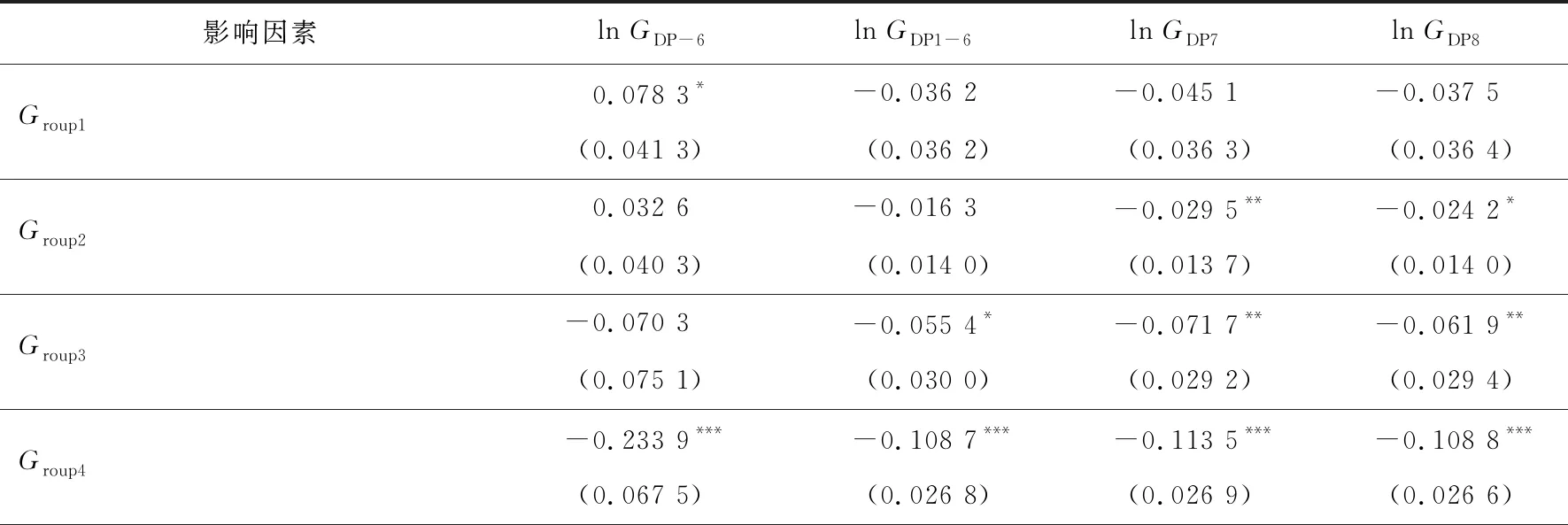
表6 高铁运营期划分距离的回归结果

2.3 机制检验

将式(1)的lnGDP替换为第二产业增加值与地区生产总值之比EGDP,式(2)的lnGDP替换为年末总人口的对数lnSpop,高铁建设期的福利范围为0～120 km,高铁运营的阴影范围为58～316 km,对高铁沿线的县域进行分析回归,判断高铁开通以何种途径引起县域经济变化,结果如表7所示。由表7可知:高铁建设期以显著促进第二产业带动县域经济发展;高铁运营期加速人口流出,加重人口迁出地区的养老负担,扩大人口老龄化对经济增长的负面冲击,且人口流动对人口迁入地区的经济增长作用大于人口流出地区,导致县域经济差异扩大。综合距离分组回归及机制检验分析,1.2节中的假设1与2均得到验证。

3 稳健性检验

对面板数据进行稳健性检验,包括变换政策时点检验和倾向得分匹配。

进行变换政策时点检验。把高铁开通看作政策实施,高铁首次运营时刻即政策实施时刻,将政策实施时刻提前几年,看回归结果是否发生改变,验证第2章结果。影响县域经济变化的因素较多,为确保结果的可靠性,需排除不可观测的潜在变量导致的内生性问题,对回归结果进行稳健性检验。为排除高铁建设期的影响,将高铁开通时间提前4 a,建设期的政策发布时间提前至高铁开始施工的前1 a进行回归,相应的各县人均生产总值的对数回归结果分别为lnGDP-4a、lnGDP-1a。

进行倾向得分匹配。因沪昆高铁各段开通时刻不同,将研究样本分为沪杭段、杭州至新晃段、新晃至贵阳段和贵阳至昆明段等4个区间。传统的倾向得分匹配法仅适用于单一政策时点的情况,无法满足沪昆高铁的分析需求,应进行逐期倾向得分匹配,在每期截面数据中都进行匹配,排除时间错配问题。采取倾向得分匹配法中卡尺内的k近邻匹配,卡尺为0.01,k=1,回归结果为lnGDP-8。检验逐期倾向得分匹配后的平稳性,所有控制变量均满足假设要求,匹配过后处理组控制变量与对照组的差异均不显著,满足平行趋势假设。

稳健性检验结果如表8所示。由表8可知:lnGDP-4a与lnGDP-1a表明高铁建设期和运营期的结果均与理论及事实相反,第2章的回归结果可靠;lnGDP-8表明高铁运营期对县域经济起显著负向作用。

表8 稳健性检验结果

4 结束语

选取2008—2020年浙江、江西、湖南、贵州和云南等5省沿沪昆高铁县域经济的面板数据,采取面板固定效应回归方法,测得高铁建设期的福利效应范围为0～120 km,与铁路沿线的距离呈反向关联;采取多期固定效应回归与渐进双重差分法相结合的方法测得高铁运营期的集聚阴影范围为58～316 km,呈∩型分布。分析福利效应机制发现,高铁建设期和运营期分别以促进第二产业发展、加速人口流动的方式影响县域经济发展。

分析高铁全生命周期下的县域经济发展,有助于县域政府及人民认识高铁和自身经济发展的关系,根据自身的地理位置和特点,发挥资源优势、地理优势和政策优势等,在高铁的不同时期分阶段采取不同措施,推动区域经济发展。

在高铁建设期,因高铁建设需庞大的资源和劳动力,为沿线县域提供大量就业岗位和发展机会,未设高铁站的县级政府应联合建筑行业积极参与高铁建设;充分发挥高铁设站县域经济自身优势,与高铁同步建设本地特色产业和配套产业,全面推动区域经济发展。

在高铁运营期,中心城市在虹吸各县域资源和人才的同时,对周边县域应进行倾斜输送和扶持发展:在政策上大力施行乡村振兴,鼓励县域建设优势产业;在经济上进行资金补助,放宽贷款要求;在技术上鼓励中心城市企业为县域提供技术支持,或在县域建立子公司,以点带面,谋求全域共同发展。县域依据本地特色优势打造独特的区域经济发展名片,充分运用互联网+资源,以优势产业构造上下游产业链,拉动县域经济。

统筹协调高铁沿线各省、各县间的经济发展,取长补短,实现资源互补。我国经济发展东快西慢,东部、中部、西部的县与县、省与省间存在经济差距,应依托高铁的交通优势,实现区域间的资源快速流通,先富带动后富,实现我国东部、中部、西部均衡发展。