基于拓扑优化的船舶舱室阻尼涂层布局分析

周凤磊,杨卓懿,欧书博,宋磊,孙彦刚,万德云

(1.山东交通学院 船舶与港口工程学院,山东 威海 264209;2.招商局金陵船舶(威海)有限公司,山东 威海 264200)

阻尼涂层是由高分子树脂、阻尼填料等组成的一种新型阻尼材料,具有黏弹性,高阻尼性使其具有较好的阻尼减振特性,被广泛应用于机械设备、航空航天、船舶等很多领域。阻尼涂层的研究,合成涂层材料的阻尼特性[1];阻尼涂层厚度与接触应力之间的关系[2];敷设阻尼涂层金属板的振动特性[3-4];阻尼涂层材料的弹性模量、阻尼损耗因子以及敷设厚度值对整体结构损耗因子的影响[5-6];一定阻尼涂层与基层板厚度比下的损耗因子[7];采用有限元法与实验相结合的方法对阻尼涂层敷设区域进行优化并验证优化结果的合理性[8]。基于以上研究,以威海船厂实船建造中所使用的阻尼涂层为对象研究其减振特性并对其进行拓扑优化以实现其布局的优化。

1 振动理论

为探究阻尼涂层对船舶舱室结构振动特性的影响,本研究利用插入损失和阻尼损耗因子2个参数[9-10]来研究其减振特性。

1.1 系统的阻尼损耗因子

系统在没有阻尼的工况下,其特征方程为

(KR-λM)φ=0

(1)

式中:KR为振动中系统储存能量的能力;λ、φ分别为实特征值和特征向量;M为系统的特征向量。

阻尼损耗因子数值大小是表征系统振动模态特性的一个关键指标。本文基于模态应变能法的理论对各种工况下的舱室结构进行计算,其公式为

(2)

式中:KI为系统耗能能力;φr为r阶模态下的模态向量。

1.2 系统的插入损失

利用插入损失研究阻尼涂层对舱室结构的减振效果,通过插入损失值可以对不同工况下舱室结构的加速度振级进行分析。

不同工况下舱室结构加速度振级的计算公式为

La=20lg(a/a0)

(3)

式中:La为振动加速度级;a为振动加速度级有效值,m/s2;a0=10-6m/s2,其表示的是基准加速度。

插入损失的计算公式为

LI=LBE-LAF

(4)

式中:LBE为基层板的振动加速度级,在本文中即为无阻尼钢板的振动加速度级,dB;LAF为敷设阻尼涂层后结构的振动加速度级。

2 船用阻尼涂层及船舶舱室模型

威海船厂建造的W0269客滚船第9甲板某舱室敷设阻尼涂层,该船总长240 m,型宽28 m,设计吃水6.2 m,设计航速22 kn,车道长度大于3 500 m,乘客定员1 200人,采用双桨设计,配备3台艏侧推,离靠港更加便捷。

阻尼涂层是威海船厂在W0270客滚船第8、第9甲板上多个舱室中所敷设的丹麦DANISH MARINE SYSTEM公司产品,阻尼涂层复合结构及在实船上的使用分别示意于图1、2,其相关性能参数见表1。作为阻尼层,与基层金属板所组成的复合结构具有较好的减振特性。

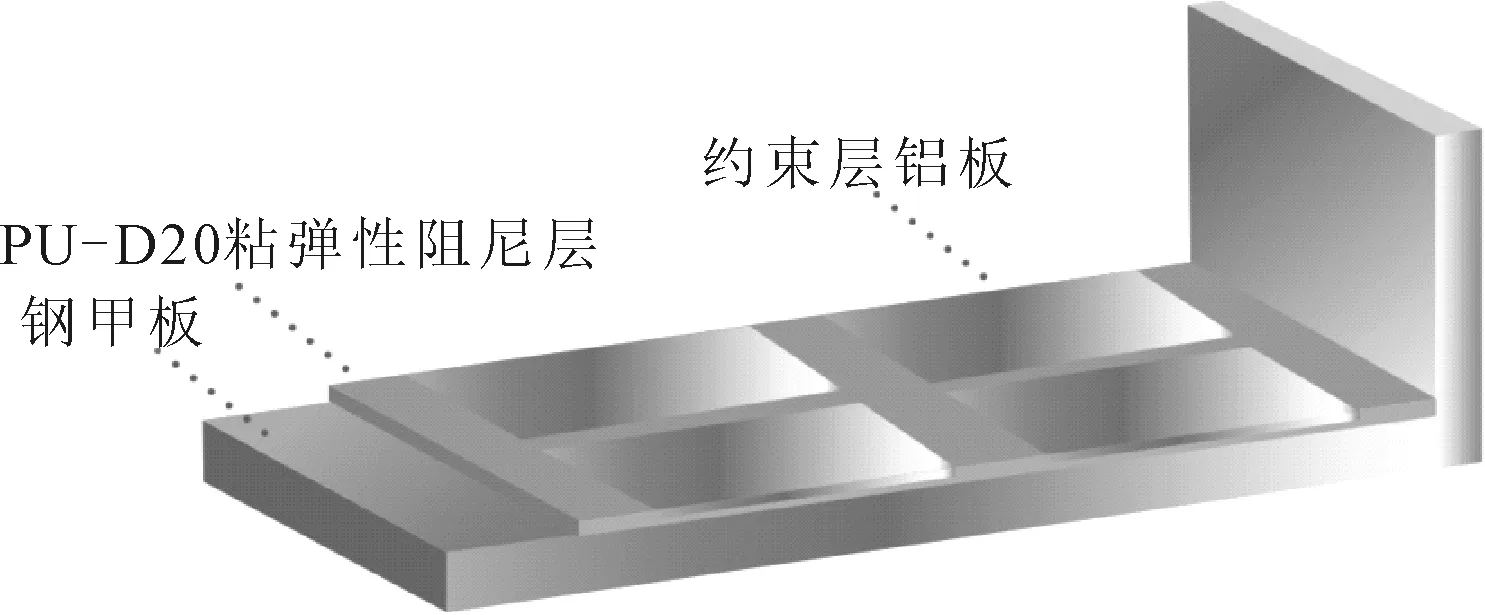
图1 阻尼涂层与船舶甲板的复合夹层结构

图2 阻尼涂层在实船上的应用

表1 各种材料参数

利用有限元分析软件ANSYS对船舶舱室进行建模和模态分析以研究船舶舱室的振动特性,根据实船上的舱室利用ANSYS建立结构模型,舱室尺寸见表2。

表2 船舶舱室尺寸 mm

船舶舱室由6个厚度为2 mm的面组成,其中前后2个面正中分别有尺寸为1 980 mm×735 mm的门和870 mm×620 mm的窗户,船舶舱室的建模选择使用实体建模,舱室在ANSYS的geometry模块中赋予2 mm的厚度,舱室模型见图3。

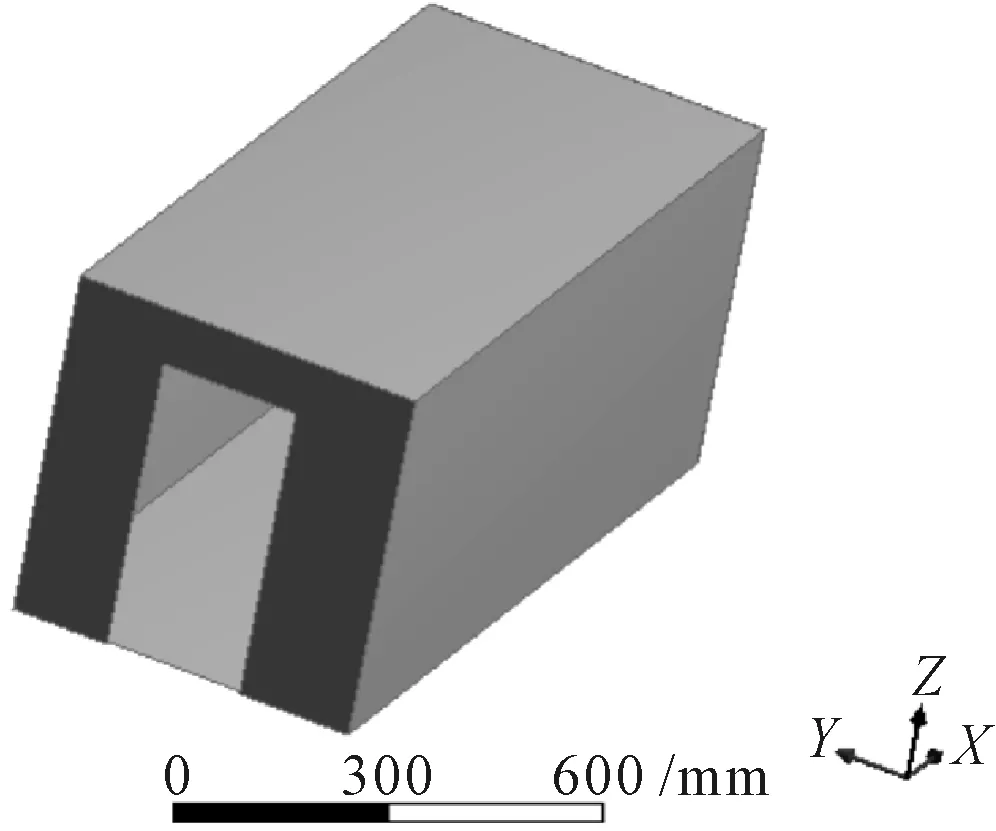
图3 舱室结构有限元模型

在舱室左壁板、右壁板、上壁板和前壁板上建立一层厚度为5 mm的阻尼涂层,该阻尼涂层的模型直接在geometry中赋予5 mm厚度,以建立敷设阻尼涂层的自有阻尼舱室结构。在船舶舱室的左壁板、右壁板、上壁板和前壁板上的阻尼涂层外添加一层厚度为0.4 mm的铝板作为约束层,铝板模型建为壳体结构以建立约束阻尼舱室结构,各材料参数见表1。

3 船舶舱室结构模态分析

无阻尼船舶舱室、敷设阻尼涂层的船舶舱室、敷设阻尼涂层同时敷设铝板的船舶舱室分别为工况一、二、三,对3种工况进行模态分析和稳态动力学分析,其阻尼损耗因子对比见表3,加速度频谱对比见图4。

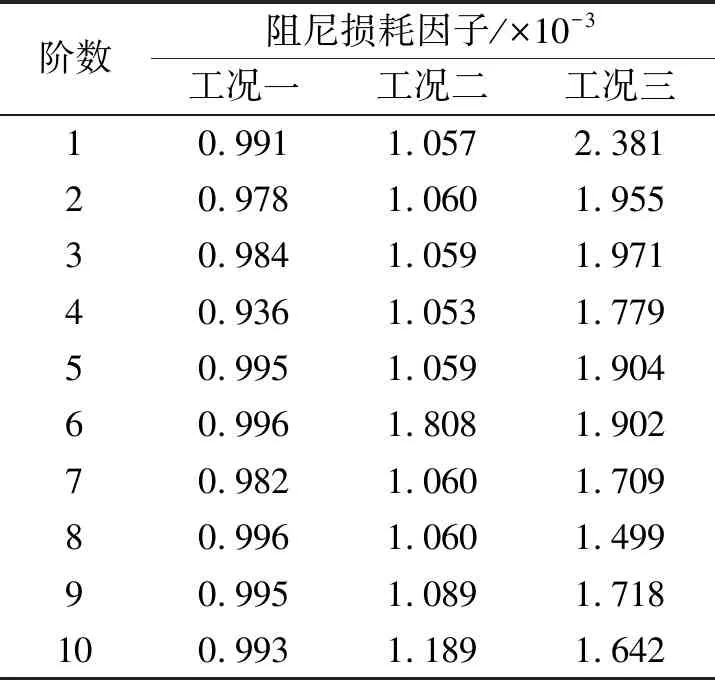
表3 各工况下舱室结构阻尼损耗因子

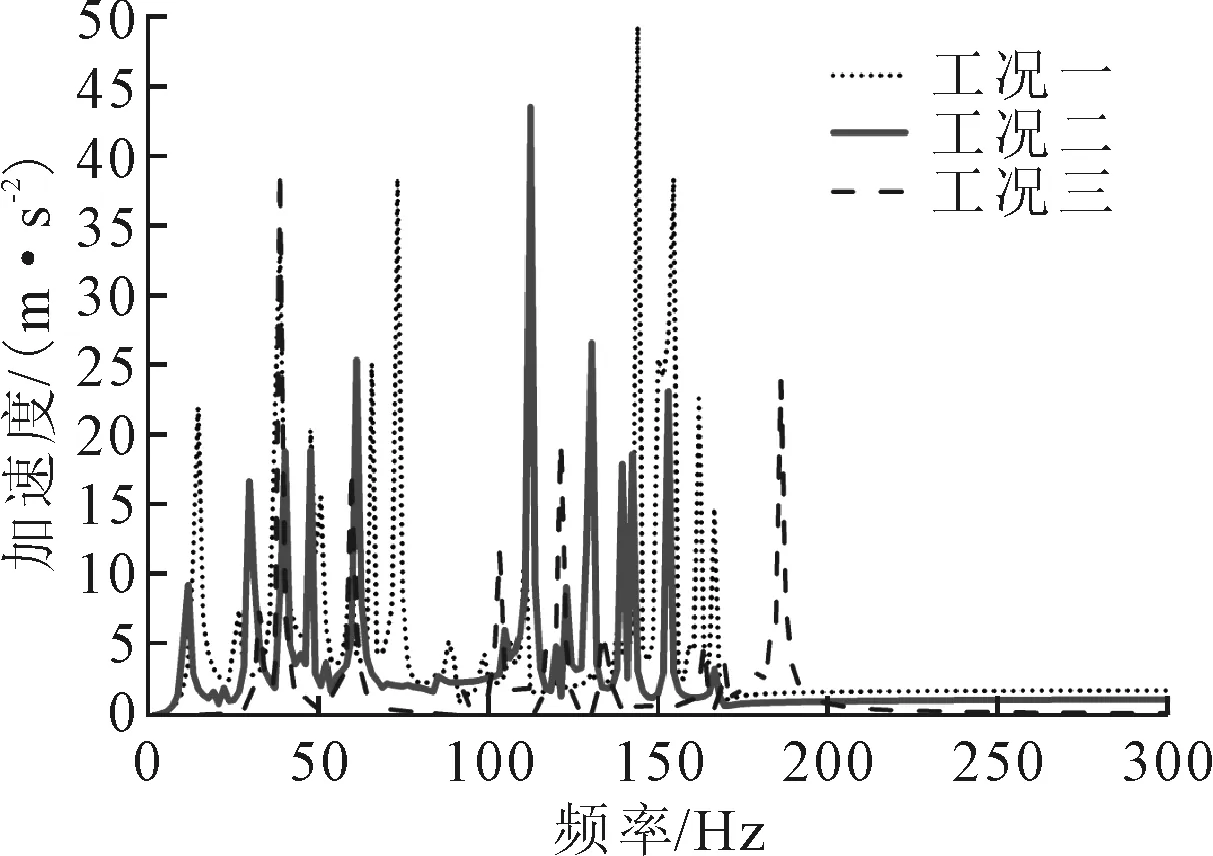
图4 3种工况加速度对比

从表3可知,工况三的阻尼损耗因子值高于工况二,工况一数值最低。工况一、工况二的平均差值为6.900×10-4,工况二与工况一差值为9.300×10-5,这也说明阻尼涂层对船舶舱室结构的减振特性同时添加约束层后效果更佳。

对比加速度频谱,工况一存在10个以上的极值点,明显多于其他两种工况,工况二的极值点个数明显多于工况三;同时工况一在位于150 Hz处出现值为接近50 m/s2的最大峰值,工况二在位于100 Hz处出现值为42 m/s2左右的最大峰值,工况三在位于40 Hz处出现值为38 m/s2左右的最大峰值。从最大峰值的数值对比来看,工况一最大,其次为工况二,工况三的最小。这也说明阻尼涂层能够实现较好的减振效果,同时在阻尼涂层外敷设铝板所构成的约束阻尼结构能够实现更好的减振效果。

4 船舶舱室阻尼涂层的拓扑优化

为进一步节省材料从而达到降低成本的目的,对船舶舱室结构约束阻尼所敷设的位置进行拓扑优化,在节省阻尼材料的同时实现良好的减振效果。

4.1 拓扑优化过程

利用有限元分析软件ANSYS对结构进行拓扑优化分析,对已建立的约束阻尼船舶舱室结构模型进行设计区域的划分,划分船舶舱室左右壁板、上壁板及前壁板四部分表面敷设的阻尼涂层及铝板约束层作为本次拓扑优化的设计区域即要进行优化的部分。同时其他部分包括钢质的船舶舱室整体结构划分为非设计区域,利用变密度法基于SIMP差值模型进行结构的拓扑优化[11-13],固定支撑位置为整个下壁板表面保持不变,设置响应约束类型为体积,定义依据为常数同时保留百分比为70%,即设置条件为减少阻尼涂层、约束层铝板原体积的30%,优化目标设置为结构前四阶模态下的阻尼损耗因子值的最大化,对约束阻尼结构进行拓扑优化,经过对结构进行迭代计算,拓扑优化的结果见图5。

图5 船舶舱室结构拓扑优化结果

图5中深灰色区域为约束阻尼材料的敷设区域,浅色为裸露出的钢质船舶舱室,从图5中可以很明显看到几个壁板表面阻尼材料的优化情况,右壁板上优化掉较大区域面积的约束阻尼材料,同时上壁板及前壁板也有一定程度的优化,尤其是舱室三壁板交界的几个顶点位置上的约束阻尼材料优化较多,而各壁板中间位置所保留的约束阻尼材料较多。

对拓扑优化后的模型重新利用ANSYS进行建模处理,主要是对优化后的约束阻尼材料进行几何形状的规则化处理,重新建模后的船舶舱室结构模型见图6,与初步优化后的模型相比,重新建模后的模型优化了约束阻尼材料的几何分布,更规则的几何形状其更有利于提高有限元软件的计算速度及实船的施工。

图6 重新建立的拓扑优化模型

4.2 拓扑优化结果

对重新建模后的模型进行模态分析,得到结构在各阶模态下阻尼损耗因子,拓扑优化后的阻尼损耗因子对比见表4。

表4 拓扑优化前后的阻尼损耗因子对比

由表4可知,优化后的结构其阻尼损耗因子值明显高于优化前,优化前后结构阻尼损耗因子差值的平均值为0.052,最大差值为1阶模态下的0.191。从阻尼损耗因子的数值表现来看,拓扑优化后的结构其阻尼减振效果明显提高。

为深入研究阻尼涂层拓扑优化后的振动特性,计算优化前后的船舶舱室约束阻尼结构的加速度频谱,结果见图7。

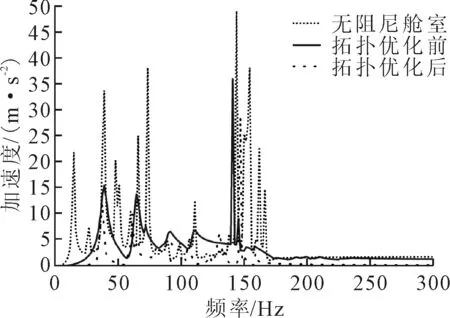
图7 优化前后的船舶舱室约束阻尼结构加速度频响应

根据各结构加速度频谱对比可知,优化后的船舶舱室结构共振峰值在150 Hz附近的频率处出现最大值,拓扑优化后其结构加速度由36.14 m/s2降至28.83 m/s2,与优化前相比降低了20.2%。同时在40 Hz及65 Hz附近频率处存在2个较小峰值,拓扑优化后的结构在该频率处的加速度分别降低了22.3%和27.3%。从结构的加速度响应来看,对阻尼涂层的拓扑优化降低了结构的加速度响应值,实现了对船舶舱室约束阻尼结构减振的目的。

船舶舱室约束阻尼结构在拓扑优化前后前四阶模态下的振型图对比见图8。由图8可知,结构在拓扑优化后其阵型出现较小的变化,这说明对阻尼材料进行拓扑优化后会对阵型产生较小的影响。

图8 拓扑优化前后振型对比

5 结论

1)对船舶舱室结构的模态分析表明,仅敷设阻尼涂层的自由阻尼舱室结构的阻尼损耗因子值在前10阶模态下均高于无阻尼涂层的钢质船舶舱室结构,同时敷设约束阻尼结构的船舶舱室结构其阻尼损耗因子值在前10阶模态下均高于自由阻尼舱室结构,能实现更好的减振效果。

2)对船舶舱室结构的加速度频谱分析表明,自由阻尼船舶舱室结构的加速度响应明显低于无阻尼的船舶舱室结构,而约束阻尼船舶舱室结构的加速度响应最大值与自由阻尼船舶舱室结构相比降低了12.55%,实现了较好的减振效果。

3)对阻尼涂层进行拓扑优化后,船舶舱室结构的阻尼材料及约束层铝板在用量减少了30%左右的前提下,最大加速度响应的峰值减少了20.2%,同时优化后的阻尼损耗因子值与优化前相比具有明显提升。对船舶舱室阻尼涂层的拓扑优化实现了减少阻尼材料用量、提升减振效果的设计目的,验证了该拓扑优化方法的可行性。