一种基于能量耗散的对接接头疲劳寿命快速预测模型

2023-08-18魏巍孙杨赵兴明陈明华邹丽杨鑫华

焊接学报 2023年8期

魏巍，孙杨，赵兴明，陈明华，邹丽，杨鑫华

(1.辽宁工业大学,锦州,121001；2.大连交通大学,大连,116028；3.辽宁省轨道交通装备焊接与可靠性重点实验室,大连,116028)

0 序言

焊接是轨道车辆关键结构连接的主要工艺，作为一种新型熔化焊方法，激光填丝焊因具有变形小、焊缝成形好、缺陷少以及接头力学性能高等优点，近年来已备受车体结构焊接的青睐[1-2].Q310NQL2-Q345NQR2 耐候钢激光焊对接接头作为轨道车辆部分关键结构连接常用的接头形式，其在服役运行过程中经常承受复杂的动态载荷，进而引发突然性的疲劳断裂，因此其服役过程的疲劳失效一直是领域内关注的重点问题.

目前焊接接头的抗疲劳设计重点关注接头的疲劳极限和疲劳寿命评估[3-4]，传统的疲劳极限评估方法主要为升降法，而疲劳寿命评估则较多采用成组法完成，这些方法不仅历时长、成本高[5-11]，而且结果往往依赖于经验性的数据统计，因而在很大程度上限制了产品性能测试的速度以及研发效率的提升.疲劳实际上是材料内微观结构在循环载荷状态下朝着损伤累积和失效方向逐渐演化的过程，这一过程表现为耗散能的持续释放，同时伴随着热力学的温升响应变化[12].随着热像技术发展的日趋成熟，使得借助红外热像仪精确获取疲劳过程的三阶段温升响应成为可能，进而为构建物理意义更为明确的能量耗散模型奠定基础.

国内外学者以能量耗散为基础做了大量的疲劳研究工作，Fan 等人[13-14]以Q235 钢为研究对象，建立了一种可实现快速预测宏微观疲劳行为的能量耗散模型，基于此模型测定了Q235 钢高周疲劳过程的能量耗散，并与其损伤变量建立了函数关系，进而对其疲劳极限进行了快速评估；Teng 等人[15]结合RVE(representataive volume element) 模型，进一步优化了Fan 等人建立的能量耗散模型，并对SAE 1045 钢的宏微观疲劳行为进行了快速预测评估;Yang 等人[16-17]进一步研发了与微结构运动相关的能量耗散模型，该模型将滞弹性和非弹性行为的分界点作为疲劳极限预测的特征点，实现了FV520B 钢疲劳极限的快速预测；Guo 等人[18-20]基于一维热传导方程，推导了一种新的能量耗散计算方法，该方法以平均温升为基础参量，可最大程度上减小计算误差，为发展精确的能量耗散计算模型奠定了基础.然而上述相关模型依赖的基础参量为第二阶段的温升增量，该参量往往需要大量的时间测得；此外上述研究主要针对非焊接金属材料展开，对于非均质焊接接头疲劳研究虽有涉及[5-11,21-23]，但其能量耗散模型尚未与疲劳过程的微结构行为建立紧密联系.

为了实现快速、精确的焊接接头疲劳性能评估，以Q310NQL2-Q345NQR2 激光焊对接接头为研究对象，以第一阶段的初始温升斜率为基础，结合ISV 模型，以期建立一种与焊接接头高周疲劳过程微结构运动联系紧密的能量耗散模型，进而为实现从能量耗散角度出发快速评估疲劳性能奠定基础.

1 基于ISV 理论的本构模型

从热动力学的角度来讲，Hemholtz 自由能是状态函数，其值可以通过获取当前的状态变量计算得到，考虑在热弹性范围内，Hemholtz 自由能有如下定义[24]，即

式中：ψ为自由能；ε和T分别为应变张量和绝对温度，是决定状态函数的观测状态变量.从式(1) 可以看出，在弹性尺度内，当ε和T两个观测状态变量(observable state variable,OSV) 确定时，其相关状态函数的值也随之确定.当材料的变形行为更为复杂时，即其变形存在不完全弹性的情况，例如滞弹性和微塑性，往往必须扩展内部状态变量(ISV)实现独立定义现有的热力学状态函数[24].

式中:T,ε,u和s分别为绝对温度、应变张量、内能以及熵流，此外ISV 变量α代表着与可恢复微结构运动相关的滞弹性行为，例如应力驱动的原子振荡和晶界处的内摩擦，而变量β则表示不可恢复微结构运动相关的微塑性行为，进而引起材料内部的损伤(图1)，这里α和β可以定义为

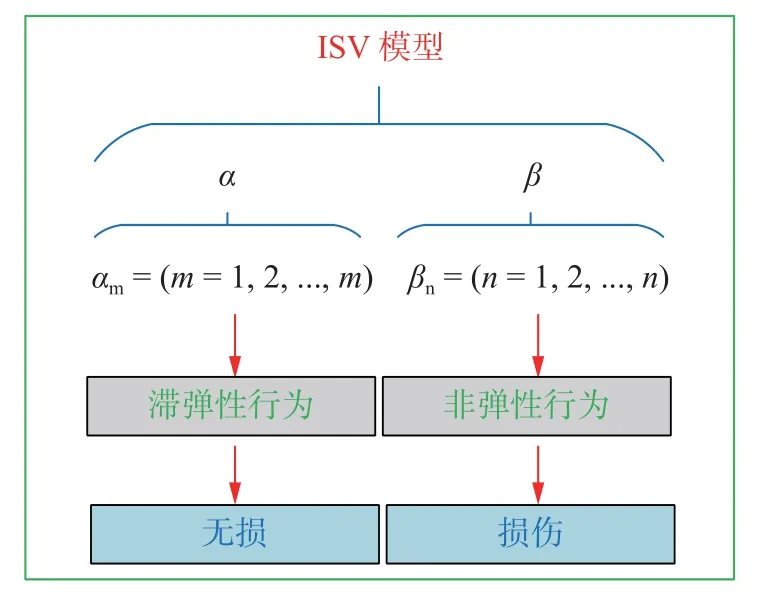
图1 ISV 模型示意图Fig.1 Schematic of internal state variable (ISV) model

2 能量耗散模型

根据热力学第一定律，疲劳过程的热平衡方程可以表示为[19]

式中:ρ和C分别为焊缝材料密度和比热；Jq为热流；d1，θthe，θinc和re分别表示为

根据文献[24]，可以推导得到

将式(8) 代入式(5)，d1可以表示为

式中：α和β为与微结构运动相关的内变量变化率，通常被视为广义热力学通量，由非平衡力A和B决定.这里出于简化目的，假设广义热力学通量α和β与非平衡力A和B之间的关系服从线性或比例关系，这个假设对于正在经历高周疲劳过程的材料来说是非常合理的，因为其仅是在平衡状态附近波动，即接近一个准静态平衡过程[25]，即

式中：man和min是独立于热力学通量和非平衡驱动力的材料常数.将式(11) 带入式(10)，得到

很多看过嘉琪跳舞的人都称她是“天才”，嘉琪却直言：“我刚开始跳舞的时候，真的很笨。一个最简单的舞蹈动作，老师一教，别的同学就会了，我却手脚僵住，整个人愣在了那里，像一个木偶娃娃。”她说上课时，最害怕听到老师说给大家10分钟的时间练习，一会一个一个到前面来跳。“一个，一个，听到这四个字，我慌的手心直出汗。”为了练出肌肉的震动感，才7岁的小女孩，却跟着成年舞者一起做俯卧撑，甚至举哑铃练体能。“累到快哭了，但老师一喊名字，就马上爬起来，咬着牙接着练习。”

式中：||•||表示矢量的欧几里得范数.从式(12) 可以看出，d1由两部分组成，即一部分由滞弹性引导的能量耗散dan(不构成损伤)，而另外一部分则是与非弹性行为相关的能量耗散(引起疲劳损伤增加)din，式(12) 变形为

对于疲劳过程来说，与材料微结构运动相关的非平衡力A和B与外加载荷以及频率有关，因此这里假设||A||2和||B||2与应力幅和频率有如下关系，即

式中：H(x) 为海维赛德阶跃函数(heaviside step function)，即当x≥0 时，H(x)=1，当x<0 时，H(x)=0；k为幂指数；uan和uin为比例系数；σc0和σc1为与材料微结构运动状态相关的两个特征应力幅值；σa为应力幅.将式(14) 代入式(13)，得到

式中：Fan(=manuanf)，Fin(=minuinf)，k，σc0以及σc1可以通过试验测定.

3 疲劳寿命预测模型

3.1 能量耗散响应

疲劳过程的温升进程由3 个阶段组成[5]，分别为初始加载的温度迅速增加阶段(Ⅰ)、热产和热耗散实现平衡的稳定温升阶段(Ⅱ) 以及因裂纹扩展引起的温升陡然变化阶段(Ⅲ)，如图2 所示.

图2 典型的疲劳温升进程示意图Fig.2 Schematic of the typical temperature rise process

对于高周疲劳过程，其某一应力水平下的能量耗散计算式为[26]

如第2 节所述，高周疲劳过程的机械能耗散主要由滞弹性和非弹性行为引起[19]，其中当应力幅小于焊接接头的疲劳极限时，其微结构运动主要为可恢复的滞弹性行为，例如轻微的原子振荡或内摩擦，不构成损伤累积；而当应力幅高于焊接接头的疲劳极限时，其微结构运动主要为不可恢复的非弹性行为，例如微塑性，构成接头内部的损伤[5].基于此，将疲劳过程中对接接头在不同应力幅水平下微结构运动的分界点定义为疲劳极限，具有明确的物理意义.

为了从宏观热力学角度量化微观尺度内的接头微结构运动行为，在第1 节里引入了ISV 内变量理论，并分别定义了与滞弹性和非弹性相关的内变量α和β，进而推导得到了高周疲劳过程的能量耗散计算表达式.结合第2 节建立的能量耗散模型，疲劳过程中不同应力幅水平下的能量耗散响应示意图如图3 所示.

图3 不同应力幅水平下的能量耗散响应Fig.3 Energy dissipation response under different stress amplitude levels

3.2 基于损伤累积的疲劳寿命预测模型

如第1 节所述，ISV 里的内变量β与引导疲劳损伤累积的不可恢复微结构运动相关，而该疲劳损伤的演化正由内部非平衡力B驱动，并在宏观尺度上表现为非弹性耗散din，因此非弹性耗散din可被视为有效的疲劳损伤指标.基于此可建立相应的累积损伤评估模型，即

式中：D为损伤参数；N为与损伤参量D对应的疲劳寿命；为能量耗散临界值，其值可以通过试验测定.对于一个原始试样来说，其损伤值D可认为是0，当载荷逐渐循环直至疲劳断裂出时，D=1，因此式(17) 变形为

式中：H−1(x) 为海维赛德阶跃函数的倒数，即当x≥0 时，H−1(x)=1，而当x<0 时，H−1(x)=∞.这里需要注意的是，当σa<σc1时，认为对接接头试样拥有无限寿命，因此依据提出的模型，关键应力幅σc1实际上可以被认为是材料内部可恢复和不可恢复微结构运动的分界应力幅，即σc1等于疲劳极限σf.

通过监测试样焊缝中心的温升增量，建立能量耗散模型，进而结合式(18) 即可实现Q310NQL2-Q345NQR2 激光焊对接接头的疲劳寿命快速预测.

4 试验方法

4.1 试验材料

采用激光填丝焊对2.5 mm 板厚的Q310NQL2耐候钢和4 mm 板厚的Q345NQR2 耐候钢进行焊接，激光器功率为6 kW 的光纤激光器，焊丝为ER50-G，送丝设备选用数字化送丝结构.焊接过程中，填充焊丝位于激光之前，激光与试板垂线的夹角为10°，保护气体为氩气，坡口形式为I 形(全焊透)，激光焊接过程示意图如图4 所示.Q310NQL2耐候钢、Q345NQR2 耐候钢、ER50-G 焊丝的化学成分以及力学性能见表1 和表2 所示.Q310NQL2-Q345NQR2 激光焊对接接头尺寸如图5 所示.

表1 Q310NQL2 和Q345NQR2 耐候钢以及ER50-G 焊丝主要化学成分Table 1 Main chemical composition of Q310NQL2,Q345NQR2 weathering steel,and ER50-G filler wire

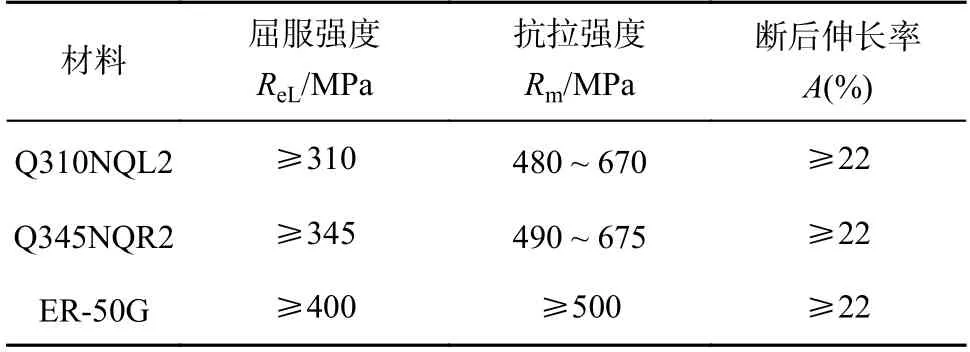
表2 Q310NQL2 和Q345NQR2 耐候钢以及ER50-G 焊丝力学性能Table 2 Mechanical propertie parameters of Q310NQL2,Q345NQR2 weathering steel,and ER50-G filler wire

图4 激光填丝焊示意图Fig.4 Schematic of laser welding with filler wire

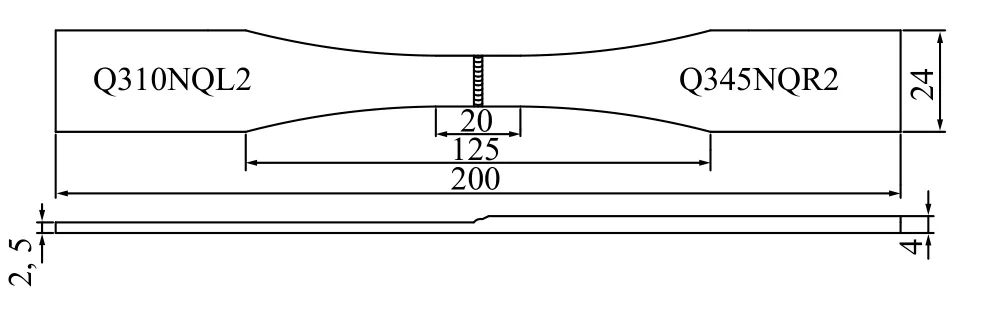
图5 Q310NQL2-Q345NQR2 对接接头尺寸(mm)Fig.5 Dimension of Q310NQL2-Q345NQR2 butt joint

4.2 疲劳试验与热像测试

根据国家标准GB/T 3075—2008《金属材料疲劳试验轴向力控制方法》在PLG-100 型疲劳试验机上对Q310NQL2-Q345NQR2 对接接头进行疲劳测试(图6)，试验频率为106 Hz，载荷形式采用单轴、正弦变化的动态载荷，应力比(R=σmin/σmax)取0.1.选用Fluke Ti450 红外热像仪对焊缝中心疲劳过程的温升响应进行全程监测，其采集图像的频率为9 Hz.疲劳试验热像测试具体试验步骤如下.

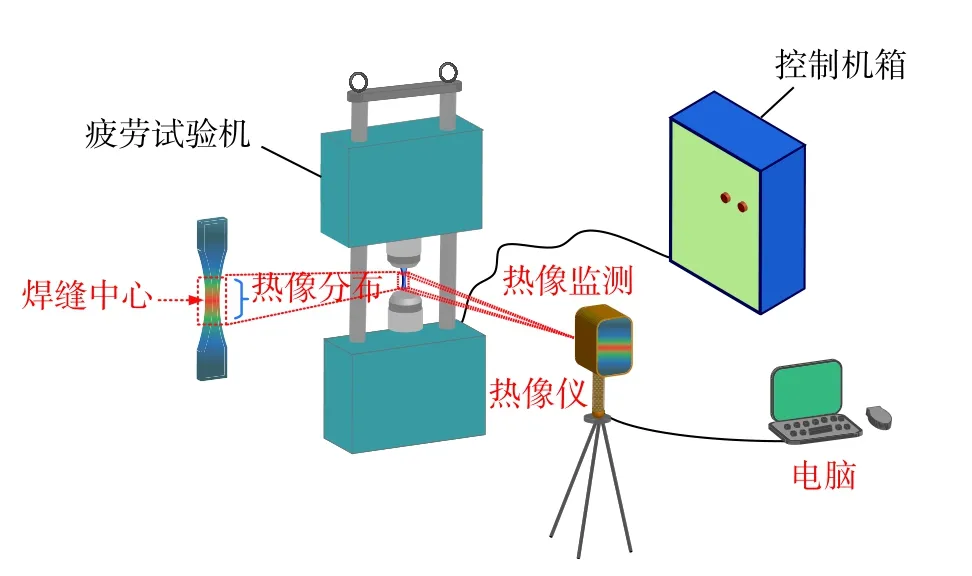
图6 热像测试与疲劳试验系统Fig.6 System of thermographic monitor and fatigue test

(1) 借助热像仪监测对接接头焊缝中心在不同应力幅水平下(σa=99.5～171 MPa) 的初始阶段温升斜率，结合式(16) 计算不同应力幅水平的能量耗散.

(2) 结合建立的能量耗散模型，计算得到不同应力幅下的能量耗散响应，进而测定Fan,Fin，k，σc0以及σc1(疲劳极限) 等参数.

5 试验结果

5.1 不同应力幅下的能量耗散响应分析

根据第2 节建立的能量耗散模型，结合式(16)计算了不同应力幅下的能量耗散值，如图7 所示.结合式(15)，采用最小二乘法对试验数据实现了较好的拟合，并对σc0，σc1，Fan，Fin以及k等参数进行了确定(表3).

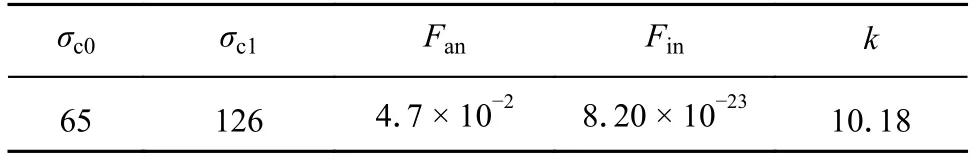
表3 能量耗散模型参数Table 3 Parameters of energy disspation model

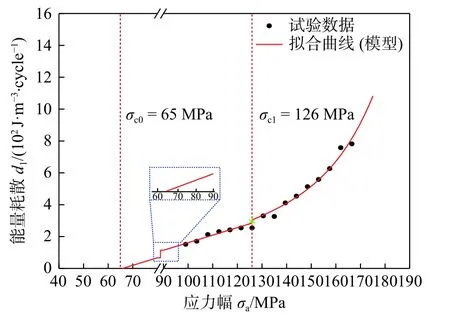
图7 Q310NQL2-Q345NQR2 对接接头在不同应力幅下的能量耗散响应Fig.7 Energy dissipation response of Q310NQL2-Q345NQR2 butt joints under different stress amplitudes

从图7 中可以看出，随着应力水平的增加，能量耗散值随之增加，且在第一类关键应力(σc0=65 MPa) 和第二类关键应力(σc1=126 MPa，即疲劳极限) 之间，其能量耗散与应力幅的依赖程度几乎是线性的；而当应力幅值超过第二类关键应力σc1时，其不同应力幅下的能量耗散响应关系呈现为非线性趋势，这与前述模型所述一致(图3).结合建立的能量耗散模型(式(15)) 对试验数据拟合，拟合的决策系数R2为0.97，这表明能量耗散模型与试验数据的一致性较高，这种较高的一致性源于两种不同的微结构演化机制，如3.1 节所述，当应力幅等级介于σc0和σc1之间，其微结构运动主要为可恢复的滞弹性行为，例如轻微的原子振荡或内摩擦，因此在该阶段其能量耗散的响应几乎是线性的；而当应力幅等级高于σc1(即疲劳极限) 时，由于不可逆微塑性行为的出现，且占该阶段微结构运动的绝大部分，使得其能量耗散响应急剧增加，且呈现为非线性的特点.

5.2 基于能量耗散的疲劳寿命预测

如3.3 节所述，疲劳过程中的能量耗散存在临界值Ec,因此结合图3 和式(19)，对应力幅为148.5 MPa 下与不可逆微结构运动相关的能量耗散临界值进行了计算，可确定为1.35 × 105J/m3.从图8 中可以看出，试样的不可逆能量耗散值基本分布在平均值加减一个标准差的范围内，这表明该临界值几乎是一个常数，与文献报道的结果一致[17].