风力机钢塔筒结构风致疲劳分析方法研究

2023-08-16童乐为郭志鑫张文莹颜峻生张学伟

工程力学 2023年8期

霍涛，童乐为，郭志鑫，张文莹，颜峻生，张学伟

(1.同济大学土木工程防灾国家重点实验室，上海 200092；2.中国建筑第八工程局有限公司，上海 200120；3.北京工业大学工程抗震与结构诊治北京市重点实验室，北京 100124)

风力机钢塔筒结构不仅承受叶片旋转导致的周期性的激励，还要承受风荷载等复杂交变荷载的持续作用，极易产生较大幅度的振动，甚至会引发疲劳问题。特别是在一些应力集中部位、易伴有缺陷的焊接部位，容易疲劳开裂并扩展，严重时会造成疲劳断裂、甚至倒塌。因此，对钢塔筒结构的疲劳寿命进行评估，是风力机钢塔筒结构设计中的一个非常重要的问题[1]。

目前，风力机结构大部分已有的疲劳评估主要集中在基础[2−3]，钢塔筒结构的疲劳问题鲜有涉及。LAVASSAS 等[4]针对1 MW 风力机结构进行了风致响应分析，在给定对应于风速范围6.32 m/s～18.2 m/s的应力幅循环次数基础上，应用名义应力法对其焊缝、预紧力螺栓和塔筒底部进行了疲劳寿命评估。刘胜祥[5]对钢塔筒结构进行风致响应分析，采用雨流计数法和Goodman 准则统计得到对称循环下的变幅应力谱，基于线性累积损伤计算得到钢塔筒结构疲劳寿命。尹艳杰[6]对钢塔筒结构在不同风速风向作用下进行动力响应分析，然后通过雨流计数法统计出疲劳验算位置处的应力幅及其相应的循环次数，结合塔筒所在场地的风玫瑰图及风速分布规律，基于S-N曲线和线性累积损伤准则，得出塔筒的疲劳寿命。柯世堂等[7]以某5 MW 风力机为例，采用谐波合成法和改进的叶素-动量理论对风力机正常运行状态的气动载荷进行模拟，对风力机塔架-叶片耦合结构进行了非线性风振时域分析。基于时程结果并结合Miner 准则对风力机关键部位的疲劳寿命进行了预测。

综上所述，可见：1)目前的风力机钢塔筒结构疲劳寿命分析研究中大都集中于采用时域方法；2)国际上权威的风力机设计软件比如GH Bladed和FAST 中疲劳寿命的计算采用的S-N曲线大都为单斜率形式的S-N曲线，这显然会导致保守的结果，即没有合理考虑低应力幅对疲劳损伤的影响；3)大部分已有的风力机专业设计软件、标准和有限元分析均没有考虑叶片的旋转效应和风向对疲劳损伤的影响。因此，有必要系统研究合理考虑叶片旋转效应、风向和低应力幅循环对疲劳损伤有折减影响的风力机钢塔筒结构在风荷载下的疲劳寿命分析方法。

本文针对风力机结构建立风致疲劳分析方法，并在某典型的风力机钢塔筒结构中加以应用。首先进行了风力机结构整体有限元建模。基于大同和化德气象站的气象数据推导得到风力机位置处的风速风向联合分布函数，在不同风速风向工况下对风力机钢塔筒结构进行风振响应时程分析，最终系统建立了合理考虑叶片旋转效应、风向及低应力幅循环对疲劳损伤有折减影响的风力机钢塔筒结构时域和时-频域疲劳寿命分析方法。

1 整体有限元模型及载荷计算

如图1 所示，本文采用主流的1.25 MW 风力机结构，位于河北张家口市张北县。限于商业保密，风机制造企业仅给出叶片的最大弦长和叶根厚度，本文基于刚度等效原则将不规则的叶片简化成矩形截面的悬臂梁形式，叶片自振频率等效之后的叶片宽度为2.86 m，厚度为64 mm，长度为54.38 m。风轮(叶片和轮毂)的质量为45 t。机舱的长为13.6 m，宽度为4.7 m，高为4.7 m，质量为85 t。塔筒为变截面钢锥筒，共分4 段，从塔底向上各段高度分别为8 m、18 m、24 m 和30 m。每个塔段的壁厚不变，从塔筒顶部向下各塔段的壁厚分别为18 mm、30 mm、42 mm 和52 mm。塔顶高度处塔筒外径为2.58 m，塔底高度处塔筒外径为4.2 m，其余各截面外径沿高度成线性变化。基础为圆截面钢筋混凝土扩展基础，直径为10 m，板厚为1.8 m。本文采用SHELL181 单元对塔筒和叶片进行模拟，分别采用BEAM189 单元、SOLID65实体单元对机舱和基础混凝土进行模拟。不同构件之间为防止相对滑移，采用耦合和约束方程的方式进行连接。研究表明：叶片和塔筒耦合效应对风振响应的影响较为显著，需要对风力机结构进行整体建模。与此同时，随着旋转谱模型用于叶片周围湍流风场的模拟，叶片旋转这一运动学问题即转化成静力学问题。基于此，有限元法开始广泛应用于风力机结构的整体建模、动力响应分析和疲劳寿命评估中。风力机结构整体有限元模型如图1 所示。

图1 风力机结构整体有限元模型Fig.1 Integrated finite element model of wind turbine structure

本文将风力机结构的空气动力荷载分为作用在叶片上的空气动力荷载和作用在塔筒上的空气动力荷载。

根据叶素-动量理论[8−9]，作用在长度为 dr叶素上的空气动力荷载 dFa可以分解为轴向推力dQx和切向力 dQy，具体表达式如式(1)所示：

式中：ρ为空气密度；c为叶素剖面弦长；Cn、Ct分别为法向力系数和切向力系数；U0为叶素位置处的合成气流速度。实际上，U0、Cn及Ct都与轴向诱导因子a和周向诱导因子b的函数。

而轴向诱导因子a和周向诱导因子b的表达式如式(2)～式(3)所示：

式中：σ=Bc/2πr，B为叶片数目；ϕ为叶素处的入流角，为a和b的函数。

基于此，作用在叶素上的空气动力荷载必须采用迭代方法来运算求解，通过对a和b赋初值开始运算直至收敛，收敛较快且计算量较小。本文通过Matlab 软件编程实现迭代进而得到气动力荷载，并考虑了叶尖、轮毂损失修正和推力系数修正。

作用在塔筒结构上的气动荷载主要考虑顺风向气动荷载FD(z,t)、漩涡脱落导致的横风向升力FV(z,t)和横向湍流分量引起的横风向气动荷载FL(z,t)。

塔筒结构顺风向气动荷载FD(z,t)采用准定常方法确定[10]，具体表达式见式(4)：

式中：D(z)为塔筒结构某高度处圆形截面的直径；CD为阻力系数，由英国工程科学数据库ESDU80025(1980)[10]的规定计算得到，综合考虑了来流湍流特性和结构表面粗糙度 ε对二维光滑圆形截面阻力系数CD的修正；U(z) 为平均风速；u(z,t)为脉动风速。漩涡脱落导致的横风向升力FV(z,t)在风速处于亚临界和跨临界区域时采用简谐升力[11]计算得到，在风速处在超临界区域时基于VICKERY 等[12]提出的升力功率谱得到。

亚临界和跨临界区域：作用在结构上的单位长度上的漩涡脱落升力FV(z,t)如式(5)所示：

式中：漩涡脱落频率ωs=2πfs，fs=US t/D；S t为斯托拉哈数，对于圆柱形截面，在亚临界和跨临界范围内，漩涡脱落出现周期脱落，S t=0.2；μL为漩涡脱落升力系数，一般由风洞试验确定，对于圆柱体，一般取μL=0.25。

超临界区域：漩涡脱落升力谱SFV(z,f)如式(6)～式(9)所示：

式中：SCL(z,t) 为升力系数的功率谱密度函数；为升力系数的方差；B为带宽参数；r′=2|zi−zj|/(D(zi)+D(zj))。

横向湍流分量引起的横风向气动荷载FL(z,t)根据HOLMES[13]提出的合成理论基于准定常假设得到，具体表达式如式(10)所示：

式中，v(z,t)为横风向湍流分量。

对于塔筒结构上的气动荷载，顺风向脉动风速u(z,t) 和横风向湍流分量v(z,t)均需依据谐波合成法通过Matlab 编程得到[14−15]，同时需判断不同塔筒高度处风速处在亚临界、跨临界区域还是超临界区域，计算较为复杂，耗时较长。

在任意风向角某一特定风速下，作用在风力机结构上的空气动力荷载示意如图2 所示。

图2 作用在风力机结构上的空气动力荷载Fig.2 Aerodynload acting on wind turbine structures

2 风速风向联合分布函数

现有的风致疲劳寿命分析仅考虑风速引起的疲劳累积损伤，忽略了风向对疲劳损伤的影响，结果较为不准确且偏于保守。为准确预测风力机钢塔筒结构在风荷载作用下的疲劳寿命，需确定风力机位置处的风速风向联合分布函数。由于商业涉密因素未能获取风电场建设区域的风资源报告，本文采用风力机位置附近的气象站观测数据推导得到风力机位置处的风速风向联合分布函数。

2.1 各风速风向区间的极值风速频率统计

本文采用的风力机结构位于河北省张家口市张北县，由于无法获得该地区地面观测站风速风向观测资料，因此需选取距离较近的气象站。受地形和海拔影响，张家口坝上与坝下地区的平均风速、主导风向差异较大。因此，在选择附近的气象站时，不仅需要考虑距离的远近，还需要考虑海拔高度、地形特征和主导风向的影响，最终选择山西大同气象站和内蒙古化德气象站的气象数据[16]。为了考虑较低风速产生的疲劳损伤，本文采用间隔8 d 抽取风速极值样本数据的统计方法。

大同气象站和化德气象站极值风速样本的频率分布见图3。从图3 可看出，两个距离较近的气象站在主导风向区间出现的概率大致相同，可近似假设风力机位置和附近气象站的风向相同。

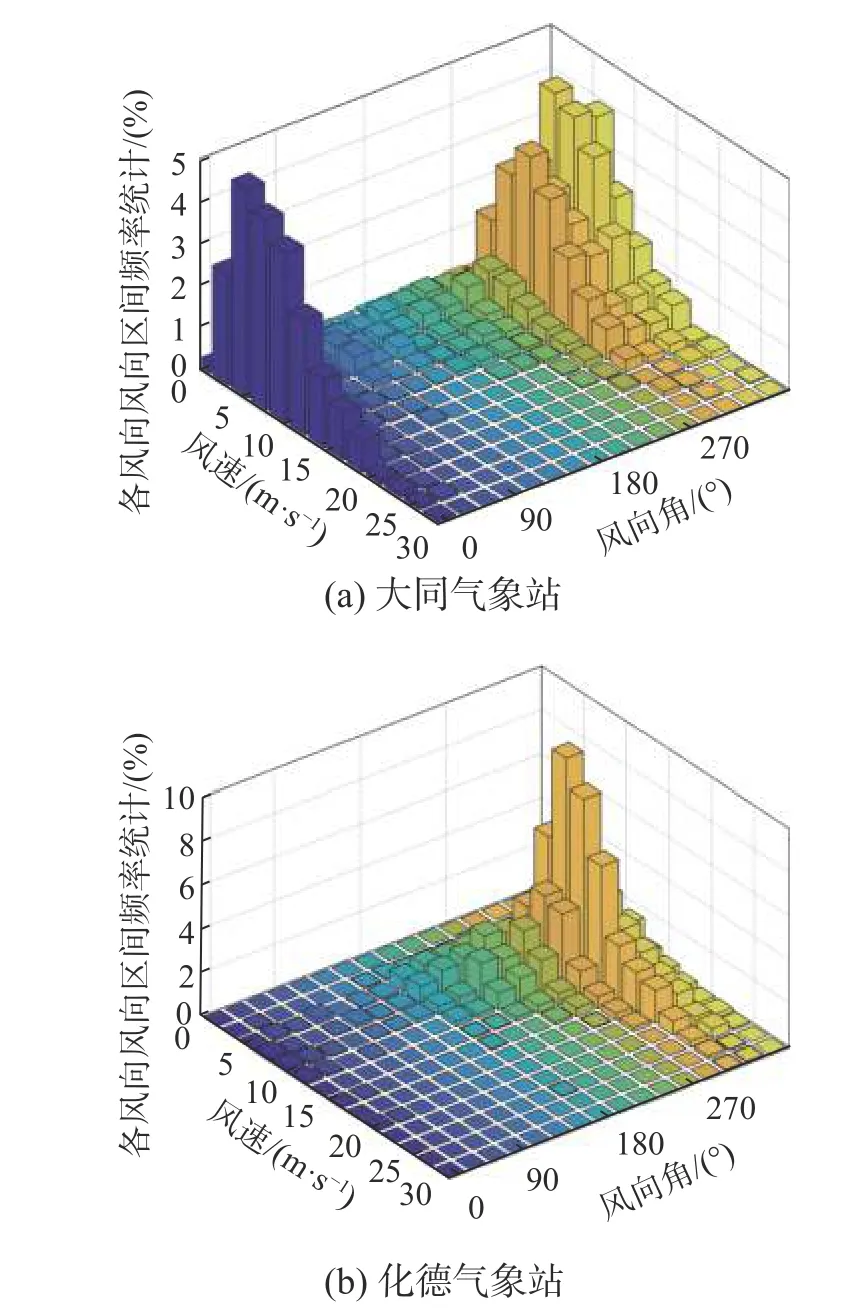
图3 气象站极值风速样本的频率分布Fig.3 Frequency distributions of extreme wind speed samples of meteorological stations

2.2 风力机位置处的风速风向联合分布函数

风速风向联合分布函数P(x, θ)可以由风向频度函数f(θ) 和各风向上的极值风速分布函数F(x)两个独立的函数共同确定，如式(11)所示：

通常极值风速的概率分布F(x)分为三种：极值I 型分布、极值II 型分布和极值III 型分布。

极值风速的极值I 型分布：

式中：a为尺度参数；b为位置参数；γ 为形状参数。

基于气象站的极值风速样本，分别采用最小二乘法、矩法等方法进行参数估计。最终大同和化德气象站极值风速样本均接近极值I 型分布。

基于风力机位置和气象站位置的梯度风速和风向相同，可推导得到风力机位置处极值I 型分布的风速风速联合分布函数，如式(13)所示：

对于本文风力机结构，可得到风力机位置处各风速风向区间极值风速样本出现的概率，如图4所示。

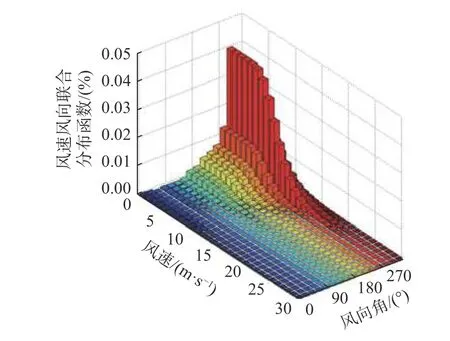
图4 风力机位置处的风速风向联合分布函数分布图Fig.4 Wind speed and wind direction distribution function at the installation location of wind turbine structures

3 钢塔筒结构的风致响应分析

由于风力机结构的强非线性特征，时域分析是业内唯一认可的风力机结构风致响应分析方法。本文采用时域分析进行风力机钢塔筒结构风振响应分析，结果的准确性通过现场实测数据进行验证。叶片旋转效应通过考虑互谱相位角影响的旋转Fourier 谱加以考虑[17]。基于此，可采用常规有限元方法进行风力机结构风致响应分析。

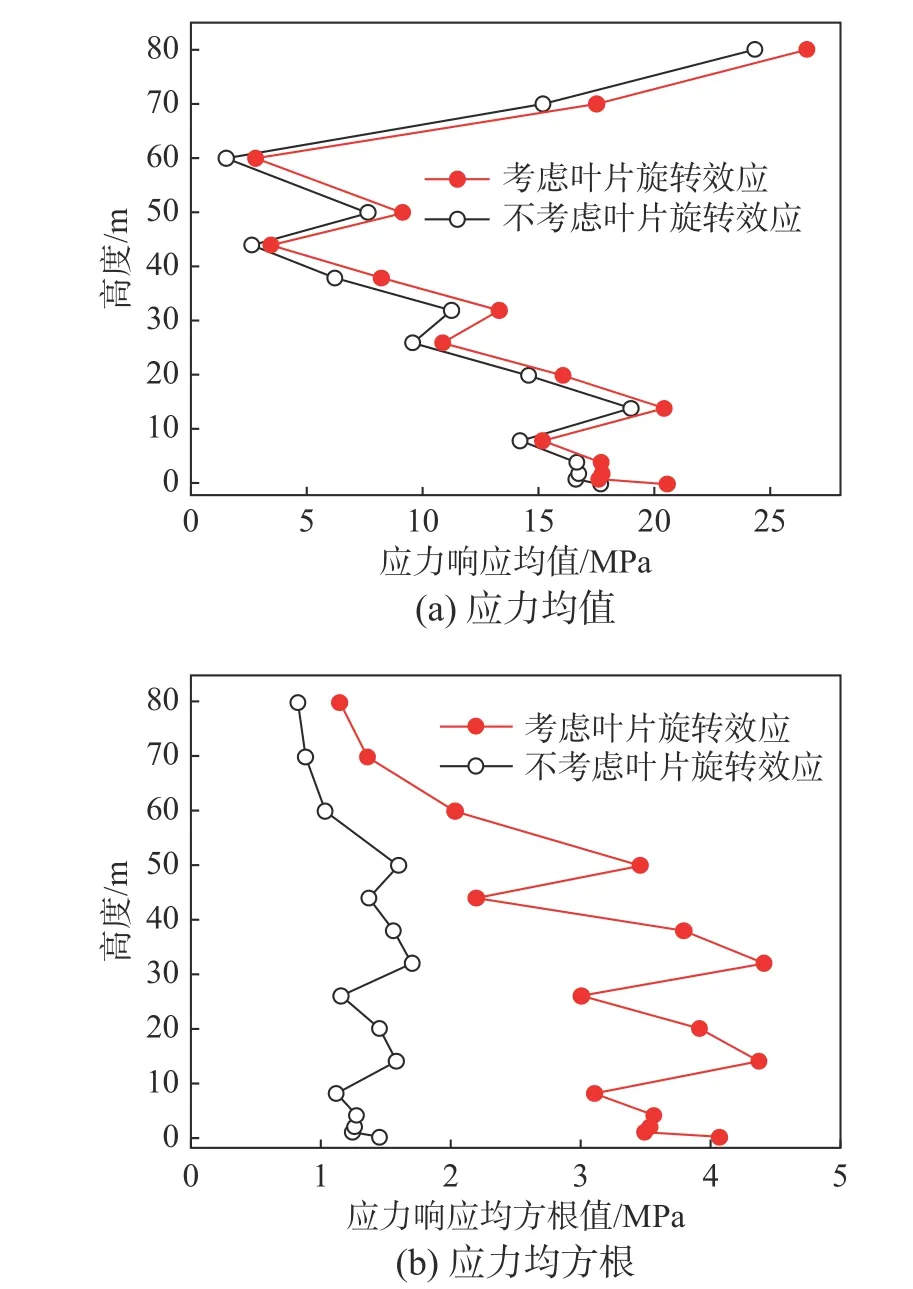
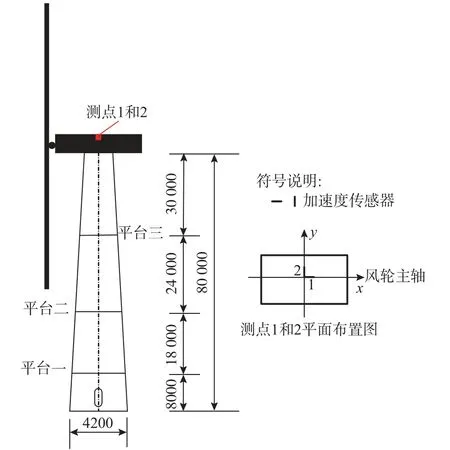
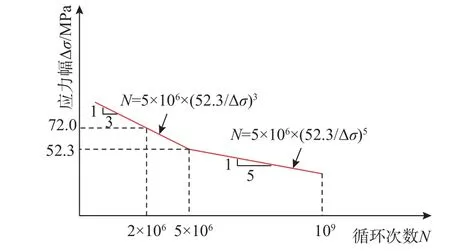
THOMSEN 等[18]研究发现疲劳损伤主要来源于风力机正常运行状态下的荷载工况，其比例占到总疲劳损伤的99.5%，风力机启动、停机和空转等设计工况几乎不影响疲劳损伤。因此，本文主要针对正常运行状态(3 m/s

3.1 叶片旋转响应对钢塔筒结构风振响应的影响

基于现场实测数据，研究发现叶片旋转效应对叶片周围的风场改变显著，造成能量重分布[17]。因此，叶片旋转效应不可避免的对钢塔筒结构的风振响应和疲劳寿命产生较大的影响。

3.1.1 沿高度和风速变化的应力响应

当风速为 16 m/s、风向角为45°时，钢塔筒结构在考虑和不考虑叶片旋转效应时沿塔筒高度方向的应力响应统计值对比见图5。叶片旋转效应对各风速对应的塔底应力响应的影响如图6 所示。

图5 叶片旋转对风力机塔筒沿高度方向的应力响应影响Fig.5 Effect of blades rotating on the stress response along height direction

图6 叶片旋转对塔筒应力响应随风速变化规律的影响Fig.6 Effect of blades rotating on the stress response corresponding to different wind speeds

从图5 和图6 可知，相对于不考虑叶片旋转效应情况，考虑叶片旋转效应对应的应力响应偏大。同时，相对于应力响应均值，叶片旋转效应对应力响应均方根值的影响更大。由于涉及商业核心机密，风力机制造商未提供叶片翼型具体的几何参数。因此，当风速超过额定风速但小于切出风速时，本文未考虑桨距角的变化对风致响应和疲劳寿命的影响。

3.1.2 疲劳验算位置处的应力响应

本文选择塔筒与门框连接区域内的A点(见图7) 的应力响应来进一步研究叶片旋转效应对塔筒应力响应的影响，对应的结果如图8 所示。

图7 风力机塔筒疲劳验算位置A 点Fig.7 Fatigue assessment for position A of wind turbine tower

图8 叶片旋转对疲劳验算位置应力响应的影响Fig.8 Influence of blade rotating on the stress response at the fatigue assessment location

从图6 和图8 叶片旋转效应导致的无量纲化的应力统计值增大幅度可看出，相较于塔筒其他位置，叶片旋转效应对疲劳验算位置处的应力响应统计量影响更为显著，特别是对应力均方根值。POWELL 和 CONNELL[19]采用美国太平洋西北国家实验室(PNL)模型(Pacific northwest national laboratory)来考虑叶片的旋转效应对叶片周围风场的影响，并与不考虑叶片旋转效应时的疲劳寿命进行对比分析，发现考虑叶片旋转效应得到的结构疲劳寿命为不考虑叶片旋转效应所得值的1/10。基于此，本文建议在计算风力机钢塔筒结构风致疲劳寿命时，必须考虑叶片的旋转效应，否则疲劳寿命预测结果偏于不安全。

3.2 与钢塔筒结构实测响应的对比

本文对风力机钢塔筒结构进行了现场实测，加速度测点布置在机舱顶部。具体测点布置如图9所示。测点1 和测点2 分别沿着机舱主轴方向(x)、垂直主轴(y)方向布置。本文选择9 个有效测试数据样本(即9 个工况)进行对比，如表1 所示。由于实测加速度响应均值和时域方法得到的加速度均值(均值为0)较为吻合，此处仅以测点2 为代表给出加速度均方根的对比，如图10 所示。

表1 现场测试数据样本(2017 年)Table 1 Field test data samples (year 2017)

图9 风力机塔筒加速度测点布置Fig.9 Layout of acceleration measuring points

图10 风力机塔筒加速度响应均方根对比Fig.10 Comparison of acceleration response RMS

从图10 可以看出，对于绝大多数工况，实测加速度响应均方根相比于时域方法得到的加速度响应均方根较大，但两者差距相对较小，均在同一个数量级上。两者存在差距的主要原因为结构建模与实际结构的差异、风力机内部各部件自身振动的影响、叶片质量偏心等因素产生的附加振动的影响。相对于其他工况，工况5 和工况6 虽然实测结果和时域分析结果存在较大的差距，但是从绝对值上看，工况5 和工况6 的实测加速度值和时域分析值相差不大。在风力机诸多附加因素的影响下，2 个工况现场实测数据和时域分析结果的差距是可以接受的且处于同一数量级上。

对比现场实测和时域分析影响数据，验证了本文风振响应时域分析方法的准确性，可用于后续风致疲劳寿命的计算。实际上，由于外部风环境的高度随机性和风力机结构附加振动的影响，现场实测和时域分析结果对比验证难度较大。鉴于目前国内外未见将风振响应数值分析结果与现场实测或风洞实验结果进行对比的情况，本文提出初步探索，认为只要保证实测加速度响应统计值和时域响应结果在同一个数量级上，即能验证风振响应时域分析方法的准确性。

4 钢塔筒结构的风致疲劳分析

本文结合风力机位置处的风速风向联合分布函数和风振响应结果，最终系统推导得到合理考虑风向、叶片旋转效应及低应力幅对疲劳损伤有折减影响的风力机钢塔筒结构时域和时-频域疲劳寿命分析理论。

4.1 变斜率两段式S-N 曲线

研究表明：在变幅疲劳状况下，应力谱中低于常幅疲劳极限的低应力幅也会对钢结构产生疲劳损伤作用。因此，目前国际上像Eurocode 3[20]和GL[21]针对钢结构变幅疲劳的计算均采用“斜率不同的双折线S-N曲线”。

对于风力机钢塔筒结构，德国劳氏船级社GL规范[21]推荐采用变斜率两段式的S-N曲线。本文选择实际工程中两个易发生疲劳开裂的部位来进行风力机钢塔筒结构疲劳寿命分析，即塔筒与门框的焊接部位以及塔筒底部与基础的焊接部位。

根据GL 规范[21]，塔筒与门框焊接位置处的构造细节与Detail category 526 相符合，对应的S-N曲线如图11 所示。

图11 疲劳验算位置A 处采用的S-N 曲线Fig.11 S-N curve for fatigue assessment position A

钢结构塔筒中的基础段塔节与钢筋混凝土基础之间通常采用基础环进行连。根据GL 规范[21]，塔筒底部与基础的焊接位置处的构造细节与Detail category 232 相符合，对应的S-N曲线如图12 所示。

图12 疲劳验算位置B 处采用的S-N 曲线Fig.12 S-N curve for fatigue assessment position B

4.2 风力机钢塔筒结构的风致随机疲劳分析理论

本文基于时域分析响应结果，分别利用时域法和时-频域法的随机疲劳理论，对风力机钢塔筒结构进行疲劳寿命预测。时-频域疲劳分析方法是先采用时域方法计算风致响应，然后采用频域方法进行疲劳分析。需要注意的是，本文针对时域法和时-频域法疲劳分析方法推导中均考虑了低应力幅对疲劳损伤的影响。

4.2.1 基于时域方法的随机疲劳分析理论

风力机钢塔筒结构基于时域方法的疲劳寿命计算公式如式(14)所示[22]：

式中，Ω为考虑低应力幅作用下疲劳损伤修正的应力参数，其具体表达式如式(15)所示：

式中：Pij为每个风速风向工况出现的概率，可由风速风向联合分布函数确定；fLij为作用在结构上单位时间内应力幅的平均次数，fLij=NLi j/ti j，NLij为第i,j工况下应力时程作用时间ti j内用雨流计数法得到的应力幅的总循环次数；f∆σm为第i,j个工况下第m级应力幅 ∆σm出现的频率，可从雨流计数法计算的应力幅频数分布直方图中得到；p为风向角的总数；q为参与风振响应计算的风速的总数；C和C′分别为高寿命区和低寿命区与材料特性有关的常数。依据德国劳氏船级社GL 规范[21]，β等于3。

Λij为考虑低应力幅疲劳损伤影响的损伤修正系数，其定义为用变斜率两段式S-N曲线形式计算所得的累积损伤度与用单斜率形式的S-N曲线计算所得的累积损伤度之比，通常 Λij的值小于1。具体的表达式如式(16)所示：

式中：∆σl为常幅疲劳极限；β′=β+2=5。

本文疲劳分析的研究对象是焊接钢结构，经分析平均应力对疲劳寿命的影响较小。因此，未针对雨流计数法得到的结果进行Goodman 修正。

4.2.2 基于时-频域方法的随机疲劳理论

由于时域分析方法计算量较大，不便于实际工程应用。本文在风振响应时域分析得到的应力响应时程基础上，通过频谱分析得到应力响应功率谱。根据功率谱密度函数通过穿越分析求得应力幅的概率密度函数，最后根据风振疲劳寿命频域分析理论估算风机钢塔筒结构疲劳寿命。该方法被称为时-频域方法，通常计算量相对较小，并且能够得到较为准确的结果。时-频域方法可分为：理想窄带法、等效窄带法、等效应力法和Dirlik 方法等。限于篇幅，各种方法的基本理论不再赘述。

考虑低应力幅作用下疲劳损伤修正后的应力参数 Ω定义如式(17)所示：

式中：

式中，f∆σij(∆σ)为低应力幅的概率密度函数。

1)理想窄带法

对于平稳高斯窄带过程，应力幅分布的概率密度函数如式(18)所示[22]：

式中，σs为应力时程响应的均方根。

根据穿越分析理论，应力幅的平均频率fLij等于应力过程的跨零率v0或者峰值率vp[22]。

经推导，损伤修正系数 Λij的表达式如式(19)所示：

2)等效应力法(平稳高斯宽带过程)

当应力过程为平稳高斯宽带过程时，∆σ=2|σp| ，σp为应力峰值。此时包含负应力幅在内的所有应力幅均被考虑。此时应力幅的概率密度函数如式(20)所示[22]：

式中：ε为带宽参数；η为不规则系数[22]。

经推导，损伤修正系数 Λij的表达式如式(21)所示：

3)考虑雨流修正的等效应力法

对于平稳高斯宽带过程，应力幅的频率分布与雨流计数法的计数原则相比仍有较大的差异，导致计算得到的疲劳寿命与时域方法相差较大，需要进行修正。因此，计及雨流修正后的期望值E(∆σβ)Wi j如式(22)所示：

式中，E(∆σβ)Rij为采用宽带过程计算的期望值。

KARADENIZ[23]给出雨流修正系数 ξi j的经验公式，如式(23)所示：

式中，g0、g1和g2均为 β的函数。

4)等效窄带法

限于篇幅，等效窄带法的基本理论此处不再赘述。

雨流修正后的应力参数 Ω如式(24)所示：

WIRSCHING 和LIGHT[24]提出计算雨流修正系数μij的经验公式，此处不再赘述。

5) DIRLIK[25]疲劳损伤公式

经推导，考虑低应力幅作用下疲劳损伤修正后的应力参数 Ω如式(25)所示：

式中：xm、D1、D2，D3、Q和R1详见文献[25]；fLij等于交变应力过程的峰值率vp。

经推导，损伤修正系数 Λij的表达式如式(26)所示：

式中：

6) Zhao-Baker 疲劳损伤公式[26]

经推导，考虑低应力幅作用下疲劳损伤修正后的应力参数 Ω和损伤修正系数 Λij的表达式如式(27)～式(28)所示：

式中：

7) Tovo-Benasciutti 疲劳损伤公式

BENASCIUTTI 和TOVO[27]提出平稳高斯过程的疲劳累积损伤表达式如式(29)所示：

式中：DNij为窄带过程的疲劳累积损伤度；DRMi j为根据Range-Mean 计数法计算得到的疲劳累积损伤度，具体表达式如式(30)所示：

权重系数ℓ 存在两种定义，第一种定义见式(31)，简称TB-1 方法。

BENASCIUTTI 和TOVO[28]认为式(28)给出的权重系数不够精确，因此提出关于权重系数 ℓ的另一种形式的表达式，见式(32)，简称TB-2 方法。

8)经验谱距修正法

TOVO 和BENASCIUTTI[27]提出采用窄带方法来近似估计宽带应力过程的疲劳累积损伤。在窄带过程的疲劳累积损伤的基础上乘以修正系数χ，具体的表达式见式(33)：

式中：DWi j为宽带应力过程的疲劳累积损伤度；DNij为与宽带平稳高斯过程具有相同应力均方根的窄带过程的疲劳累积损伤度；(χ)ij为经验谱矩修正系数，(χ)ij=。

4.3 风力机钢塔筒结构的风致疲劳寿命结果

表2 为时域方法及所有时-频域方法计算得到的疲劳寿命。本文采用时域分析方法来作为风力机塔筒结构疲劳寿命计算的参考基准。

表2 钢塔筒结构风致疲劳寿命计算结果汇总Table 2 Summary of fatigue life calculation based on different methods

图13 和图14 为时-频域方法和时域方法的疲劳累积损伤沿风向角和风速的变化规律对比。图15给出了时域方法得到的各风速风向工况累积损伤三维柱状分布图。

图14 疲劳累积损伤随风速的变化规律Fig.14 Fatigue accumulation damage versus wind speed

对比图4、图13 和图15 可以看出，风向对结构的风致疲劳累积损伤影响较大，在风向出现概率较大的区间产生的风致疲劳累积损伤较大。同时，从图14 可看出，当风速介于16 m/s～24 m/s区间时，钢塔筒结构风致疲劳累积损伤较大。

从表2、图13 和图14 可以看出，采用风致疲劳寿命时-频域分析理论比时域分析方法计算得到的疲劳寿命偏小。相对于时域分析法得到的疲劳寿命，采用雨流修正后的等效应力法最为精确，其次是TB-2 和Dirlik 公式，理想窄带法的计算结果最不精确。值得注意的是，采用理想窄带法、等效窄带法、Zhao-Baker 公式和未经过雨流修正的等效应力法算得的疲劳寿命不满足风力机设计对塔筒最低使用寿命为20 年以上的要求。特别是理想窄带法和等效窄带法计算结果过于保守(目前认为是宽带应力过程疲劳寿命的下限值)，最终影响到风力机设计的经济性。

综上所述，在实际工程设计中，推荐采用风致疲劳时域分析方法，此方法能同时兼顾风力机设计的安全性和经济性要求，但计算量较大。

如果在设计时，需要方便快捷的预测钢塔筒结构的疲劳寿命，同时预测结果需具有较高的精度且偏安全，本文建议采用雨流修正后的等效应力法、TB-2 和Dirlik 公式进行分析计算。

如果在设计时只需要粗略估算钢塔筒结构的疲劳寿命，本文建议采用经验谱矩修正法，该方法虽然缺乏理论基础，但是计算较为简便，也不失较高精度。