锚索式悬浮隧道断索动力响应及安全设计分析

陈政阳，何晓阳，邵永波，项贻强，郭赵元

(1.西南石油大学土木工程与测绘学院，成都 610500；2.浙江师范大学浙江省城市轨道交通智能运维技术与装备重点实验室，金华 321004；3.浙江大学建筑工程学院，杭州 310058；4.江苏省交通工程建设局，南京 210004)

悬浮隧道(Submerged floating tunnel, SFT)是一种连接海峡、江河湖泊等深、长水道的新型结构形式。它基于阿基米德原理悬浮在水下一定深度，通过节段预制、水下对接拼装，逐步从海峡一端向另一端建造，并利用与海床基础相连的张紧锚索限制其变形。与大跨径桥梁、沉埋隧道相比，悬浮隧道具有跨径更大、路线纵坡更小、单位长度造价更低以及运营阶段受外部因素影响更小等独特优势，因此，成为21 世纪最具竞争力的跨海交通结构[1−3]。

悬浮隧道所处的深水环境复杂多变，除受到波流、温度梯度、车辆移动荷载作用外，营运过程中还面临诸如地震、外部冲击碰撞、锚索涡激共振等多种极端作用威胁。DI PILATO 等[4]提出一种适用于非线性动力分析的五自由度平面铰接单元来模拟水中悬浮隧道的锚索，综合流体与结构的耦合、结构与土的耦合效应，研究了意大利Messina海峡悬浮隧道方案的地震响应。MAZZOLANI 等[5]结合中国千岛湖的悬浮隧道概念设计，基于ABAQUS/Aqua 平台模拟了隧道在环境荷载下的动静态响应。XIE 和CHEN[6]建立了三维的悬浮隧道-峡谷水系模型，研究了峡谷水系对水平地震波的传递效应。罗刚等[7]建立了波浪-地震联合作用下悬浮隧道管体-锚索系统的振动模型，研究了波浪参数、地震的方向和峰值加速度对于悬浮隧道系统响应的影响规律。HE 等[8]针对适用于水深小于100 m 水域的墩柱式悬浮隧道，建立了结构地震响应的半解析分析模型，探讨了管段间柔性接头的减震性能。陈健云等[9− 10]考虑锚索的垂度效应，建立了悬浮隧道锚索-管体刚性节段的耦合非线性参数振动模型，研究了激发系统参数振动、涡激振动的条件。孙胜男等[11]建立了锚索非线性随机振动方程，采用蒙特卡罗数值模拟法对随机激励作用下锚索的振动响应进行了研究。惠磊等[12]综合考虑流体作用和系统阻尼，采用等效质量法建立了悬浮隧道节段冲击荷载作用简化理论模型，并进行了数值验证。杨赢等[13− 14]提出了悬浮隧道在碰撞作用下的整体动力响应数值模拟方法、简化理论模型，并进行了试验验证。罗刚等[15−16]研究了悬浮隧道在近场非接触爆炸荷载作用下的运动学规律，之后又建立了一套考虑水下爆炸和车辆载荷的耦合模型，分析了爆炸-车辆联合作用下的悬浮隧道动力响应，并利用既往的测试数据对该耦合模型进行了验证。ZOU 等[17]研究了琼州海峡海域可能发生的海啸、台风灾害对悬浮隧道的水动力特性影响，研究表明：超强台风比海啸对悬浮隧道更具破坏性，并进一步给出了较圆形、椭圆形更优化的管体截面形式。MIN 等[18]为克服传统传感器及测量手段在悬浮隧道水下锚索损伤探测应用中的困难，提出了一种基于卷积神经网络(CNN)的锚索损伤检测方法。WU 等[19]基于波流水槽和特制的小型振动台装置进行了悬浮隧道模型试验，研究了地震-波浪-水流共同作用下管体-锚索节段的振动情况。以上研究成果从多个方面，为悬浮隧道防灾减灾提供了科学理论依据。

进入21 世纪以来，工程结构因局部构件失效进而连续倒塌的事故时有发生，更多学者开始关注大跨径空间结构(如弦支穹顶)、缆索承载桥梁(如斜拉桥)、平面桁架等在受拉杆件突然断裂时的结构响应与安全对策研究[20−22]。部分规范也对结构抗连续倒塌设计提出了要求，如美国PTI (Post-Tensioning Institute)协会在斜拉桥规范[23]中明确斜拉桥在任何一根拉索失效时仍能保持足够的安全性，并推荐变换荷载路径法(Alternate load path method,AP method)，取动力放大系数等于2.0，将断索引起的静力效应放大来考虑断索引起的冲击效应。这种方法原理可行、操作简便，但部分学者也在研究中发现仅依靠“动力放大系数”单一指标，难以描述结构中不同构件承受的冲击效应，同时其取值为2.0，可能出现计算过于保守、或不安全的情况。

WOLFF 等[24]研究了局部拉索失效引发的斜拉桥动力学行为，结果表明：对于加劲梁的弯曲响应，动力放大系数可能小于2.0。CAI 等[25]将AP 法引入到斜拉桥局部断索响应计算，对1 根或2 根斜拉索的失效进行了动力分析，研究表明：拉索失效的静力、动力仿真结果之间存在很大差异，同时认为2.0 的动力放大系数是静态分析过程中尚可的取值。张羽等[26]针对一座未竣工的大跨混凝土斜拉桥断索事故进行了案例分析，研究了断索对斜拉桥主梁内力、塔顶位移、剩余拉索索力产生的冲击效应，并给出不同物理量的动力放大系数取值范围大致在1.02～2.05 区间。HOANG 等[27]进行了单根斜拉桥拉索的横向冲击-破断试验，研究表明：该工况下斜拉桥动力放大系数将大于2.0。王霄翔等[28− 29]进行了弦支穹顶局部环索的断索动力试验，研究表明：拉索构件的动力放大系数可能出现远大于2.0 的情况，同时提出将“冲击系数”作为“动力放大系数”的补充，评估拉索构件承受的冲击效应。张超等[30− 32]首先通过理论推导验证了多自由体系“动力放大系数>2.0”的可能性；其次，基于AP 法提出了多重环索-张弦组合屋盖的断索冲击静、动力分析方法，研究了拉索失效对于此类新型索支穹顶结构的刚度、内力及极限承载能力的影响规律；之后，还对断索动力分析的关键参数(如锚索失效时间、结构阻尼等)进行了敏感性研究，通过有限元动力分析得出部分构件动力放大系数显著大于规范推荐值2.0 的结论。

作为一种缆索承载体系，锚索是悬浮隧道的关键受力构件，在海水腐蚀、疲劳荷载以及其他外部因素的影响下可能出现局部断索事件，锚索骤断一旦发生，必然引起管体强烈振动以及剩余锚索索力的提高。XIANG 等[33]完成了静水条件下悬浮隧道局部断索模型试验，验证了适用于细钢丝的断索试验装置可靠性，讨论了锚索失效后剩余结构的内力重分布规律。WU 等[34]在波流水槽中进行了悬浮隧道节段在动水环境下的锚索失效动力响应试验，分析了多根锚索连续失效的关键影响因素。

为了研究锚索式悬浮隧道断索效应的动力响应规律并给出抗断索安全设计的技术路线，首先在有限元软件中建立了断索事故发生前，悬浮隧道在管体剩余浮力、锚索预张力作用下的初始状态；之后，进行了隧道跨中截面单根锚索骤断的数值模拟，并依据动力放大系数和冲击系数评估了断索冲击效应；同时，通过动力放大系数和冲击系数，将断索静力效应放大，进行了结构的安全设计分析。本文提出的分析框架及最终得到的动力评价指标建议取值，可为悬浮隧道与类似结构形式的抗断索设计提供参考。

1 悬浮隧道断索响应分析的技术路线

图1 给出了悬浮隧道断索响应动力分析与安全设计的流程框图。首先确定结构参数，建立有限元模型；对部分锚索施加预张力，得到恒载作用下悬浮隧道的“初始响应S0”；之后分为两种途径讨论锚索突发失效引起的剩余结构响应：

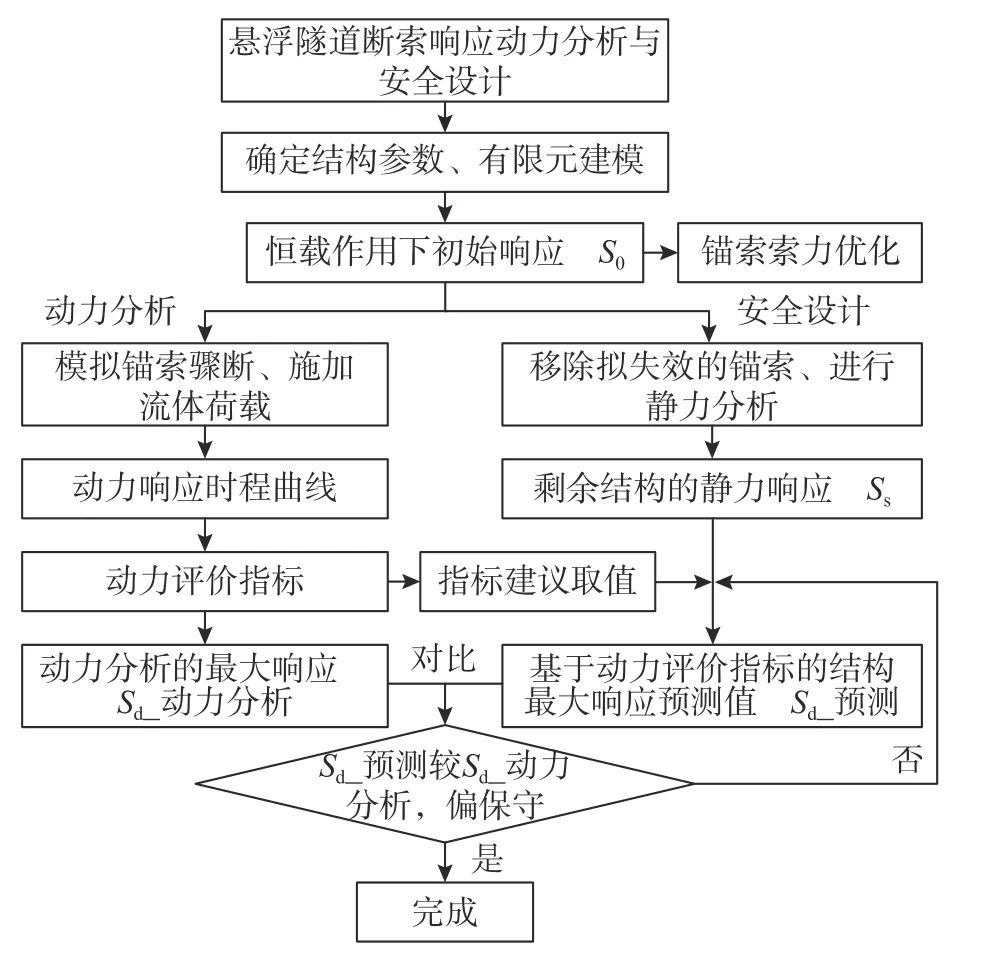
图1 悬浮隧道断索响应安全设计技术路线Fig.1 Technical route of safety design for SFT subjected to cable loss response

1)全过程数值动力分析方法，获取剩余结构的时程曲线，直接求解断索后的最大响应“Sd_动力分析”。该方法计算精度高，但对于复杂、精细化的有限元模型，动力分析成本较大。

2)在模型中删除拟失效的锚索单元，依然进行静力分析，得到“剩余结构的静力响应Ss”；再通过“动力评价指标”公式，间接求出断索后最不利响应的预测值“Sd_预测”，从而指导悬浮隧道的抗断索安全设计且计算量大幅减小。其核心在于动力评价指标的选取与合理取值，以确保安全设计得出的“Sd_预测值”较“Sd_动力分析”偏向保守。

2 悬浮隧道恒载初始状态

2.1 算例参数

目前，世界范围内还没有悬浮隧道建成实例，本文所取的结构参数基于文献[16, 19, 35]，如表1所示。悬浮隧道的总长度为1000 m。管体材料为钢筋混凝土，外直径15 m，壁厚1 m，可在管体内部进行隔断，以满足公路、铁路运营以及通风、疏散通道的布置。管体弹性模量取为3.45×104MPa。阻尼比按钢筋混凝土结构取为1.5%。

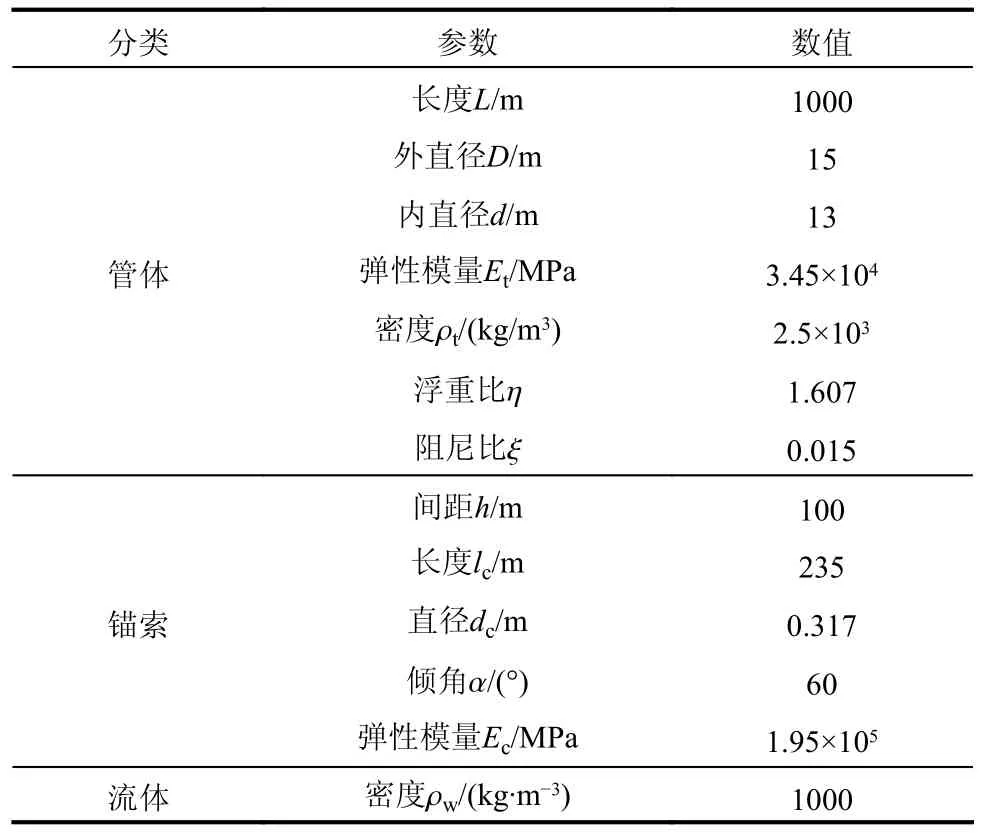
表1 悬浮隧道算例基本参数Table 1 Basic parameters of the SFT in this case study

锚索间距为100 m，长度235 m，锚索垂直深度约为200 m，属于建造悬浮隧道适用的深海区域。有关锚索倾角的合理取值，许多学者从不同角度进行了研究，总体认为45°～60°是一个合理区间。锚索直径0.317 m，以钢绞线材质确定锚索的弹性模量为1.95×105MPa。

2.2 有限元模型建立

在ABAQUS 软件中，建立悬浮隧道有限元模型，并考虑锚索失效过程中的结构几何非线性受力历程。隧道管体采用B31 梁单元，锚索采用T3D2 桁架单元模拟，模型共计1037 个节点，划分1018 个单元。隧道的两端为“简支”边界条件，锚索与管体节点之间采用MPC BEAM“刚臂”连接，锚索与海底的连接边界条件为“铰接”。有限元模型及锚索编号如图2 所示。

图2 悬浮隧道有限元模型Fig.2 Finite element model of the SFT

2.3 断索前初始状态确定

现有的悬浮隧道振动研究一般忽略了结构在恒载作用下的初始状态，而直接输入外部动荷载。然而，悬浮隧道锚索构件突然失效引起剩余结构振动的动态过程中，并不承受具体的动力荷载，而是与完好结构的恒载受力状态直接相关，所以在断索响应分析前首先需要建立初始状态。

对有限元模型施加恒载(由表1 可得，单位长度管体剩余浮力为654.24 kN/m)之后，锚索失效动力分析之前，首先通过调整锚索索力(即对部分锚索施加预张力)，使得悬浮隧道达到一个相对受力更佳的恒载初始状态。这里把“索力相对均匀、尽量减小驳岸段支承反力”作为调索目标。

图3 给出了调索阶段施加的锚索预张力以及调索前、后锚索拉力与两端支座反力的分布情况。

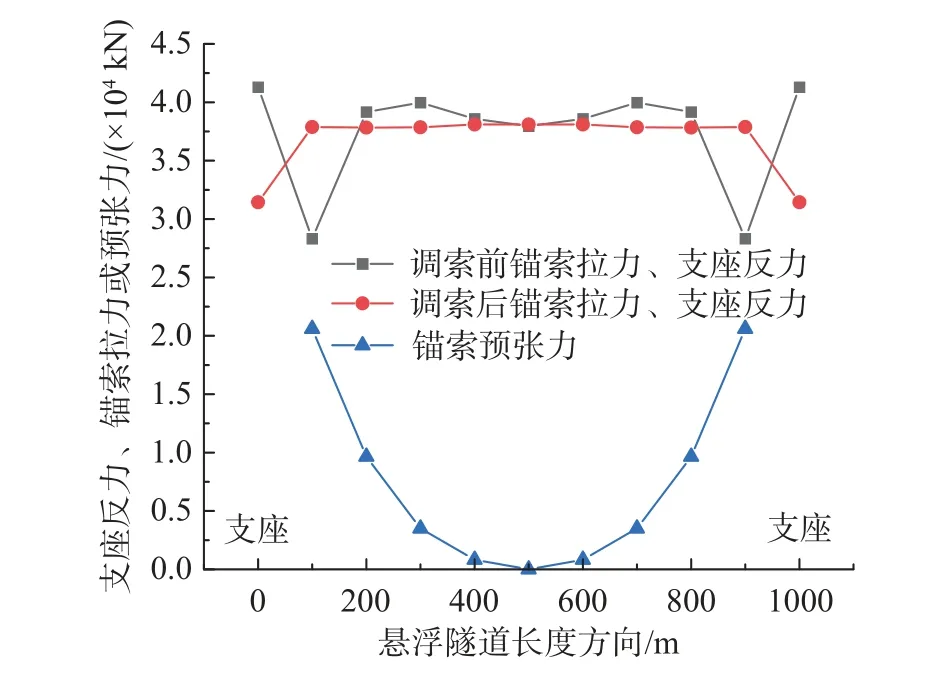
图3 锚索预张力及恒载作用下调索前、后的索力对比Fig.3 Pretensions acted on anchor-cables and cable forces with or without the pretensions under dead load

由图3 可知，施加管体剩余浮力后，由于悬浮隧道两端支承的边界效应，端部锚索拉力较跨中附近锚索更小；经过调索，支座反力大幅减小，锚索索力趋于均匀，集中在3.80×104kN 附近，锚索应力约为480.78 MPa。

图4 还比较了调索前、后，恒载作用下悬浮隧道管体的竖向位移、弯矩。如图4 所示，调索前，管体靠近两端支座处的变形、弯矩较大；调索后，靠近支承处的管体竖向变形更为平缓，管体正、负弯矩分布更加均匀。此时，管体跨中x=500 m 位置处，竖向位移为0.672 m，竖向弯矩为4.445×108N·m。

图4 恒载作用下调索前、后管体竖向位移与弯矩对比Fig.4 Comparisons of the vertical tube displacements and bending moments with or without cable-force adjustments under dead load

本文阐述的索力优化思路，能为实际悬浮隧道工程提供参考。不过对于更大跨径、多对锚索布置的悬浮隧道，索力调整将是一个更加复杂的过程，应根据多重调索目标(如管体纵坡要求、管体控制弯矩、变形等)全方位考量。

3 断索响应动力分析

3.1 断索动力分析

如图4(a)所示，调索后，悬浮隧道跨中变形突出，且合拢段施工难度大，是整个结构较薄弱的部位，因此将断索工况设定为悬浮隧道跨中x=500 m 截面断一根索(5a 号锚索)。

以断索前初始状态为动力响应分析的起始点，通过*MODEL CHANGE 命令移除有限元模型中的失 效 锚 索，锚 索 失 效 时 间 取 为0.01 s[36−38]，在ABAQUS/Implicit 模块中进行隐式动力分析。利用ABAQUS/Aqua 模块，基于Morison 方程加载流体作用力[5,39]，包括流体附加质量力、流体阻力，取附加质量系数为CA=1.0，取拖曳力系数为CD=0.6[14]。采用瑞利阻尼定义结构阻尼。

悬浮隧道运营阶段，始终受到波浪、洋流以及移动车辆等动荷载的作用，但从文献[35, 40]的研究结果来看，这些常规动力作用的量值与悬浮隧道恒载、断索效应相比非常小，因此本文暂没有计入水流与移动交通荷载的影响。

3.2 动力分析结果

采用两种动力评价指标—“动力放大系数(DAF, Dynamic amplification factor)”，“冲击系数(DC, Dynamic coefficient)”，评价构件失效导致的冲击效应[29]，定义如下：

式中：S0为断索前恒载作用下结构响应；Sd为断索后动力响应最大值；Ss为剩余结构完成内力重分布后的静态响应，或是断索引起的剩余结构静力响应。

3.2.1 管体位移

悬浮隧道跨中x=500 m 处单根锚索失效后，此截面的竖向位移时程如图5 所示。可见断索引起的结构振动非常明显，位移由恒载作用下的0.672 m 在第一个振动周期内达到最大值1.067 m。随着能量耗散，锚索骤断约150 s 后，结构响应趋于断索后的内力重平衡状态，此时跨中位移为0.922 m。由式(1)、式(2)计算可得：悬浮隧道跨中截面竖向位移动力放大系数为1.58，冲击系数为1.59。

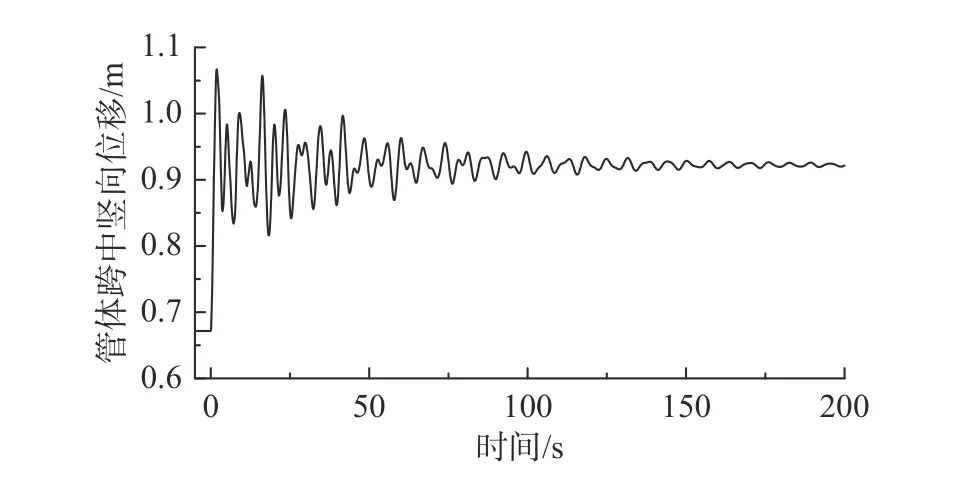
图5 断索后悬浮隧道跨中截面竖向位移时程曲线Fig.5 Vertical displacement time history curve of the SFT at the mid-span

为了解跨中单根锚索断裂对于悬浮隧道整体变形的影响，图6 给出了断索后管体竖向最大位移包络图与内力重平衡状态的变形图。可见断索冲击效应，引起了x=300 m～700 m 范围内管体的较大形变。x=300 m、700 m 处管体的竖向位移动力放大系数为3.02，冲击系数为1.15。

图6 悬浮隧道跨中截面断索时的管体竖向变形包络图Fig.6 Vertical deformation envelopes of the SFT tube due to cable breakage at the mid-span section

3.2.2 管体竖向弯矩

图7 还给出悬浮隧道承受的竖向最大弯矩包络图和内力重分布时的弯矩图。如图7 所示，管体弯矩响应受到的断索冲击效应影响范围，较管体位移更小，只在x=420 m～580 m 范围内弯矩的增长明显。

图7 断索过程中管体竖向弯矩包络图Fig.7 Envelope curves of the vertical bending moment of SFT tube during cable breakage

断索引起的结构振动过程中，跨中x=500 m截面的竖向弯矩最大值为1.174×109N·m，内力重平衡状态下的弯矩为8.442×108N·m。竖向弯矩动力放大系数为1.26，冲击系数为−2.64。

由于初始状态和内力重平衡状态的管体竖向弯矩方向相反，冲击系数出现负值。这说明对于悬浮隧道这种细长同时伴有一系列锚索支承的高次超静定结构，不宜采用冲击系数表征在锚索失效位置处，管体弯矩承受的断索冲击效应。

3.2.3 剩余锚索索力

为研究跨中单根锚索骤断后，剩余锚索索力的动态响应，图8 给出了两根具有代表性的剩余锚索索力时程曲线(即失效锚索同侧且相邻的4a 号锚索，失效锚索对侧的5b 号锚索)。

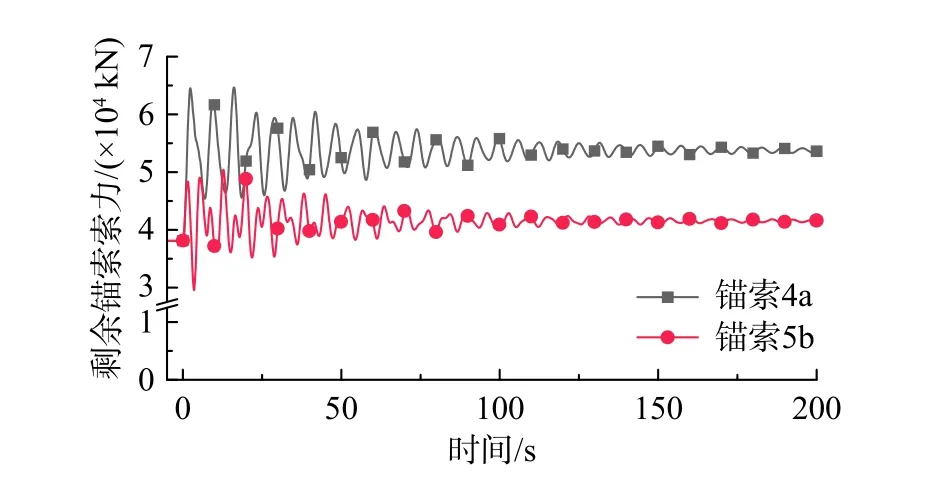
图8 典型的两根剩余锚索索力时程曲线Fig.8 Time history curves of the cable tensions of the two typical remaining anchor-cables

如图8 所示，由于锚索索力与管体的空间运动密切关联，4a 号锚索索力振动曲线的趋势与5b 号锚索区别较大。4a 号、5b 号两根锚索初始状态的索力均约等于3.809×104kN，4a 号锚索的动力放大系数、冲击系数分别为1.70、1.70；5b 号锚索的动力放大系数、冲击系数分别为3.57、1.32。其中5b 号锚索的振动曲线，还呈现出张拉力减小的阶段，索力减小对悬浮隧道的安全是非常不利的，易导致锚头的脱开，或是结构整体的失稳，这说明恒载作用下的锚索索力不宜过小。

进一步将剩余锚索索力的动力放大系数、冲击系数汇总于图9。从图9 可以看出，部分剩余锚索动力放大系数远大于规范取值2.0[23]，甚至出现负值。这是因为动力放大系数的计算式，分子、分母同时去除了恒载作用下结构响应(式(1)中的S0)的影响，导致动力放大系数指标对于悬浮隧道锚索这种涉及强非线性振动的构件不具备参考价值。而剩余锚索索力的冲击系数处于1.12～1.70 范围内，一方面可用于评价剩余锚索受到的断索冲击效应，另一方面也可指导锚索构件的安全设计。

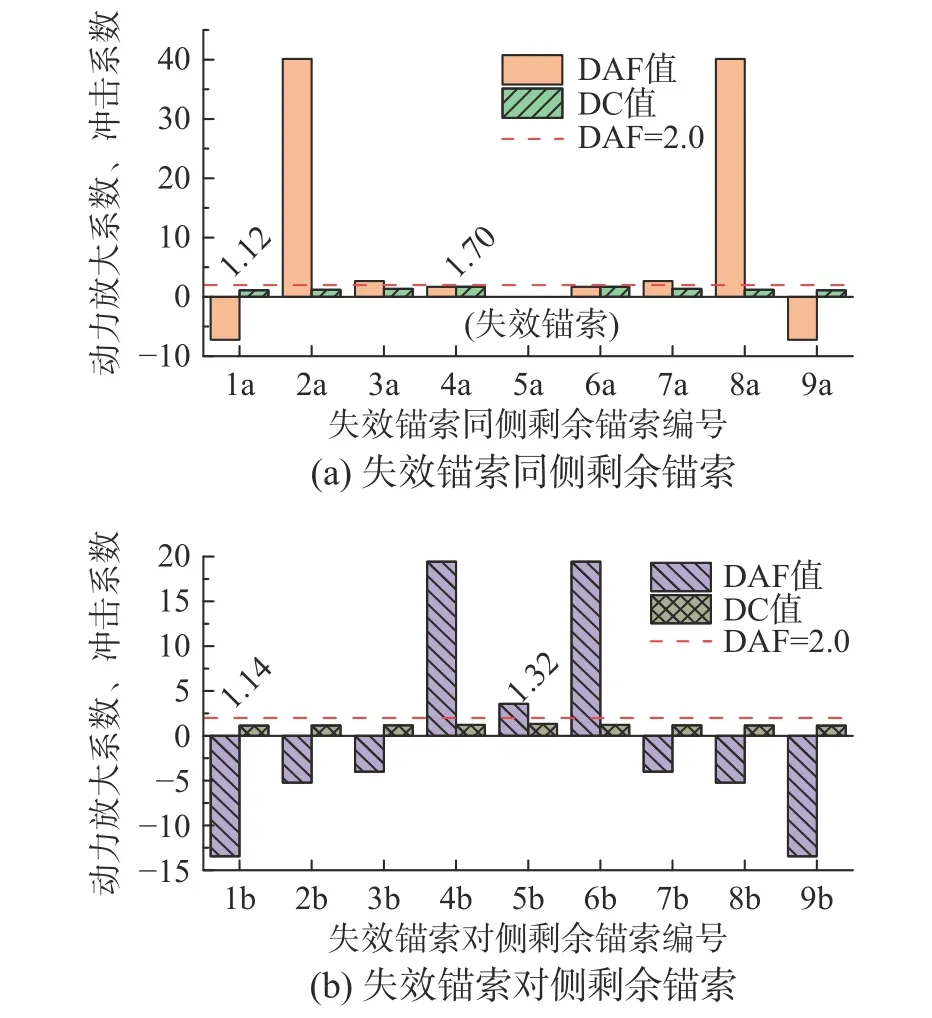
图9 剩余锚索索力的动力评价指标Fig.9 Dynamic evaluation indexes of the tensions in the remaining anchor-cables

4 基于动力放大系数、冲击系数的断索响应安全设计

规范中一般取动力放大系数等于2.0[23]；对于冲击系数的取值尚无相关规定，参考3.2 节的管体位移、弯矩和索力的冲击系数计算值，再叠加额外安全系数进行处理。动力计算已求出跨中断索截面竖向位移冲击系数为1.59，后文偏安全地暂取1.8。

4.1 管体变形

将分别采用动力分析、安全设计方法得出的管体竖向变形包络图绘制于图10。

图10 动力、安全设计方法得出的管体竖向变形包络图对比Fig.10 Comparisons of the vertical deformation envelopes of the SFT tube from dynamic or safety design method

可见，以“动力放大系数取2.0”的安全设计结果较为贴近动力分析，在管体变形较大的x=375 m～625 m 范围内，其结果较动力分析数据稍大。而以“冲击系数取1.8”的安全设计方法，则在除跨中断索位置外，与动力分析有较大差距。

总的来说：基于动力放大系数的安全设计，能够较好地反映出锚索断裂效应引起的悬浮隧道最大变形；而基于冲击系数的安全分析过于保守。

4.2 管体弯矩

图11 给出了基于动力放大系数取2.0，冲击系数取1.8，两种安全设计方法的管体竖向弯矩与动力分析的比较。由于断索前、后，跨中截面管体竖向弯矩变号(由管体下缘受拉变为上缘受拉)，但基于冲击系数的预测结果是将初始状态响应S0等比例放大，无法反映出断索截面承受的最大弯矩。而基于动力放大系数取2.0 的安全分析，在断索位置附近x=420 m～580 m 范围，较好地覆盖了动力计算结果。

图11 动力、安全设计方法得出的管体竖向弯矩包络图对比Fig.11 Comparisons of the vertical bending moment envelopes of the SFT tube from dynamic or safety design method

此外，对于距离断索位置较远的部分(0 m～400 m，600 m～1000 m)，基于动力放大指标的管体最大弯矩预测值与动力分析结果的曲线趋势一致，但数值上存在一定差距。建议可采用动力放大系数、冲击系数两个指标分析结果中绝对值较大的数据，作为设计参考值。

4.3 剩余锚索索力

图12 给出了基于动力放大系数取2.0，冲击系数取1.8，两种安全设计方法的剩余锚索最大索力及其与动力分析结果的比较。对于失效锚索同侧的剩余锚索，基于动力放大系数取2.0 的剩余锚索最大索力分布趋势，与动力结果较为贴近，4a 号锚索最大索力预测值均与动力结果接近。而对于失效锚索对侧的剩余锚索，动力放大系数取2.0 的最大索力预测值偏小，基于冲击系数取1.8 的预测值则具有更大的冗余度。

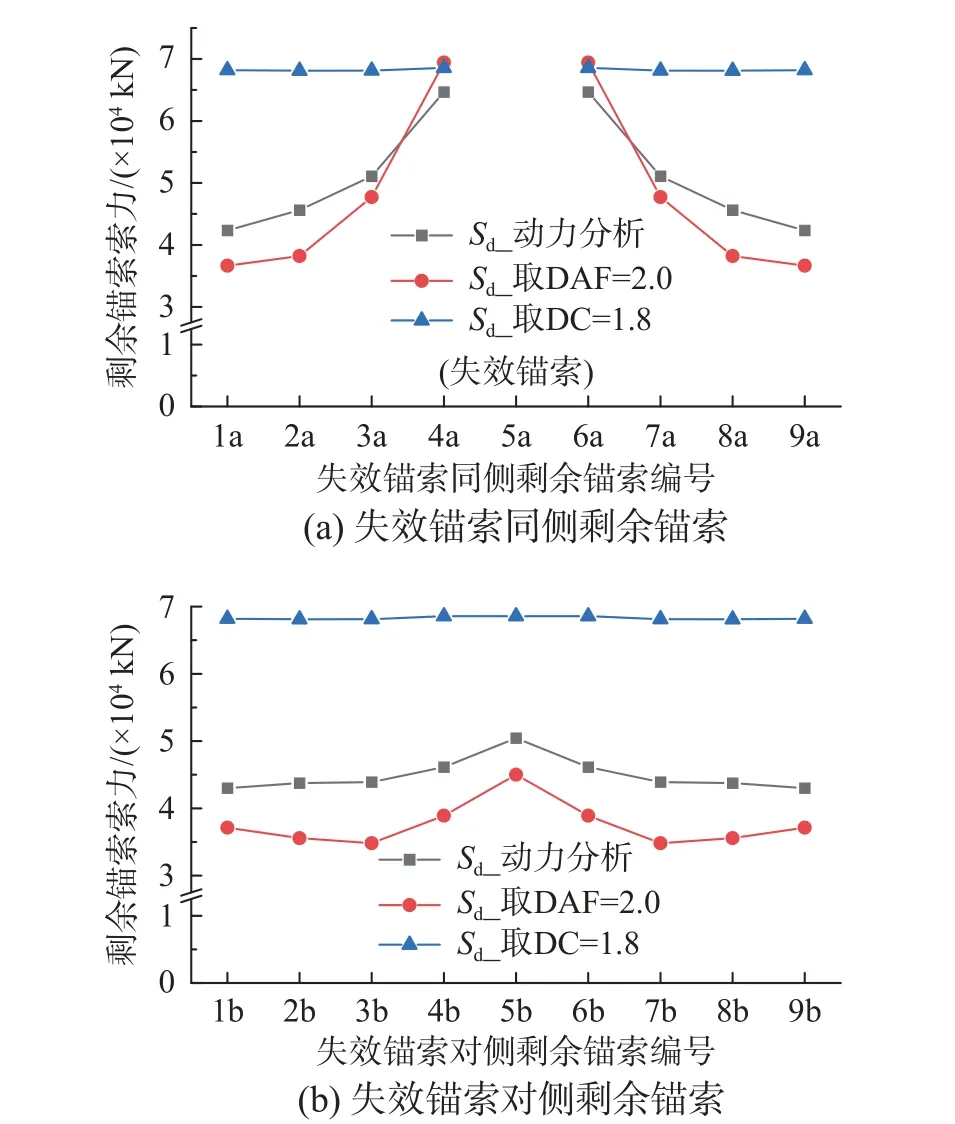
图12 动力、安全设计方法得出的剩余锚索最大索力对比Fig.12 Comparisons of the maximum tensions of the remaining anchor-cables from dynamic or safety design method

5 结论

本文针对锚索式悬浮隧道的结构特点，提出了出现锚索骤断事故时的结构动力响应与安全设计分析框架。首先通过ABAQUS 软件建立了悬浮隧道在恒载作用下的初始状态，进而模拟了局部单根锚索失效情况下的结构整体动力学行为，评估了悬浮隧道承受的断索冲击效应；并且基于动力放大系数、冲击系数提出了断索响应设计建议，减小计算成本的同时获得较动力分析偏安全的结果。通过上述研究，得出以下结论：

(1)对部分锚索施加预张力，使得悬浮隧道恒载作用下初始状态的索力分布均匀，管体的变形、弯矩减小。

(2)局部断索引起的结构振动非常明显，且影响范围较大，悬浮隧道跨中断索截面竖向位移、弯矩的动力放大系数分别达到1.58、1.26。

(3)悬浮隧道管体位移、弯矩的断索响应安全设计，宜结合动力放大系数方法，取值为2.0。

(4)预测断索过程中悬浮隧道锚索的最大索力，取冲击系数为1.8，受拉锚索构件的安全储备更高。