灰狼算法优化的PID控制器在实验焦炉温度控制中的应用
2023-08-15白敬一李忠峰马新茹
白敬一 李忠峰, 马新茹 李 东
(1.中唯炼焦技术国家工程研究中心有限责任公司,2.营口理工学院,3.华能营口仙人岛热电有限责任公司)
在炼焦过程中,焦炉温度的控制对于焦炭的质量至关重要,同时影响炼焦效率。焦炉加热过程具有大惯性、大滞后等特点,采用常规算法难以取得良好的控制效果。通常采用PID控制器控制焦炉温度。PID控制器的原理是通过反馈来调整控制参数,从而实现温度的稳定控制。具体来说,PID控制器根据测量值与设定值之间的误差,分别调整比例、积分和微分参数,从而使温度稳定在设定值附近。
然而,在焦炉温度控制中,PID控制器的参数选择对控制系统的性能有重要影响。对于传统的PID参数调节方法,主要依靠经验或试错的方式,效率低且很难保证最优解的搜索。因此,研究如何寻找最优PID控制器参数的优化算法,成为了焦炉温度控制领域的一个热点问题。
近年来,随着智能优化算法的发展,越来越多的研究者将其应用于PID控制器参数优化中。智能优化算法具有搜索速度快、收敛性好、适应性强等优点,在实际应用中表现出了较好的性能。其中,粒子群算法、遗传算法等经典智能优化算法已经得到了广泛的研究和应用。例如,高宪文[1]等人通过模糊控制优化PID控制器参数,实现了焦炉温度的精确控制。文献[2-4]采用混合遗传算法和模拟退火算法优化PID参数,实现了对焦炉温度控制的优化。近年来,灰狼优化算法也被引入焦炉温度控制领域。灰狼优化算法[5]是一种模拟自然界灰狼社会行为的智能优化算法,具有全局寻优、高效性和易于实现等优点。雷平[6]等人采用模糊控制方法优化PID参数,实现了仪表温度智能控制。
1 中小型实验焦炉温度控制系统
1.1 中小型实验焦炉温度控制系统介绍
中小型实验焦炉的设计首要原则是试验结果准确,尽量贴近工业焦炉生产状态,试验数据能与生产数据建立良好的相关性;其次要有稳定的试验结果,试验重现性好;另外尽量实现机械化、自动化,操作方便灵活可靠。
该中小型实验焦炉是通过电加热使温度升高到目标温度。为了控制温度,需要使用PID控制器来调节电加热器的功率。实验焦炉温度控制系统包括传感器、控制器和执行器,能够实时监测焦炉内部温度,并根据设定的目标温度,自动调节焦炉加热器的功率,以维持温度在设定范围内,该温度控制系统如图1所示。
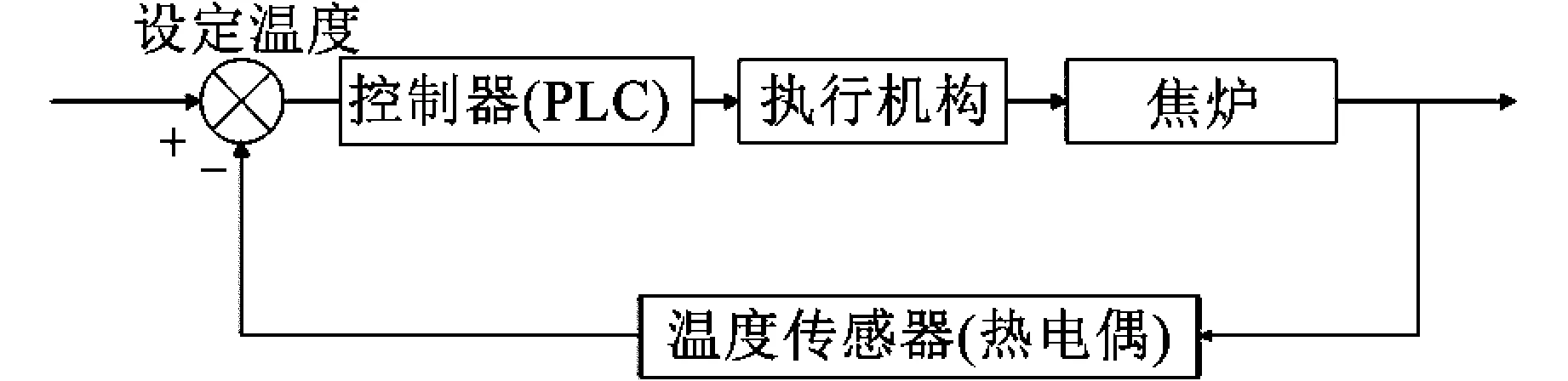
图1 中小型实验焦炉温度控制系统
1.2 中小型实验焦炉温度控制数学模型
在焦炉温度控制研究中,常将焦炉温度看作被控参数,并对其进行数学建模。基于实验结果和现场经验,可以将实验焦炉温度简单等效为二阶带有纯滞后的数学模型。
(1)
式中:T(t)为实验焦炉温度;K为传递函数的增益;T1、T2分别为一、二阶惯性环节的时间常数;Td为纯滞后环节的时间常数;s为复变量;q(t)为热量输入,是控制器的输出。
2 灰狼优化算法优化PID控制器
2.1 灰狼优化算法介绍
灰狼算法(Grey Wolf Optimizer,GWO)是一种基于自然界灰狼群体行为特点的启发式优化算法,由Seyedali Mirjalili等人在2014年提出。GWO模拟了灰狼群体在协作寻食过程中的个体互动和集体智能,以解决优化问题。
灰狼算法的基本思想是将解空间视为一个灰狼群体(α,β,δ,ω)的生态系统,每只灰狼代表一个解,灰狼之间的相对位置代表解的质量,灰狼之间的交互和协作代表解的搜索过程。灰狼算法包括三个基本行为:寻觅猎物、对抗群体、领袖指挥。其中,寻觅猎物是灰狼在生态系统中寻找猎物的基本行为,对抗群体是灰狼之间的竞争和协作过程,领袖指挥是灰狼群体中领袖的指挥行为。灰狼算法的核心是如何更新每只灰狼的位置和状态。每只灰狼根据自身位置和当前的群体信息,更新其位置和状态,从而寻找更优的解。灰狼之间的交互和协作可以通过灰狼的距离和灰狼之间的相对位置来表示,通过更新灰狼的位置和状态,如图2所示,可以使整个群体向更优解的方向演化。
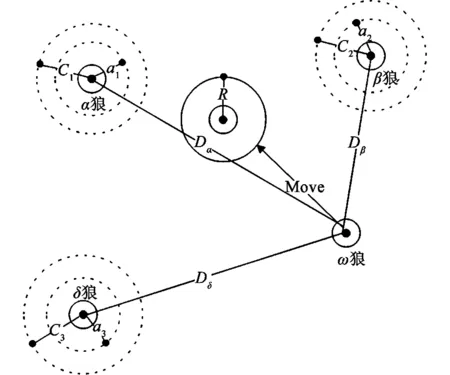
图2 灰狼算法各狼位置更新原理
灰狼在捕猎过程中会包围猎物,对包围猎物行为进行数学建模,数学方程为:
(2)
(3)
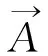
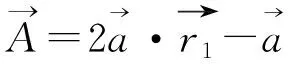
(4)
(5)
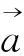
狩猎行为见公式(6)到公式(8):
(6)
(7)
(8)
2.2 灰狼优化算法改进的PID控制器(GWO-PID)
PID控制器是一种常见的反馈控制器,可以根据输出与目标之间的差异来调节控制器输入,从而使系统达到期望状态。PID控制器具有三个参数,即比例系数、积分系数和微分系数,这些参数的优化对于控制系统的性能至关重要。为了优化PID控制器的参数,通常使用计算机模拟或实验设计方法。在计算机模拟中,使用数学模型模拟电加热实验焦炉的温度变化过程,并通过灰狼优化算法来寻找最佳PID参数。可通过设计一系列实验来寻找最佳参数组合。
PID控制器的输入是系统目标输出yr(t)与实际输出y(t)之间的偏差e(t),控制器的输出是u(t),即:
e(t)=yr(t)-y(t)
(9)
(10)
式中:Kp为比例系数;Ki为积分系数;Kd为微分系数。
以单位阶跃信号为输入,观察系统的阶跃响应特性,分析系统的超调量、调节时间、稳态误差等性能指标。采用性能指标ITAE作为GWO算法的适应度函数,表达式为:
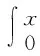
(11)
根据实验焦炉的温度特性,将其简化为一个具有纯滞后的二阶系统。然后,构建相应的PID控制器模型,并定义适当的目标函数,以求取控制系统最佳性能。其灰狼优化算法流程图见图3。
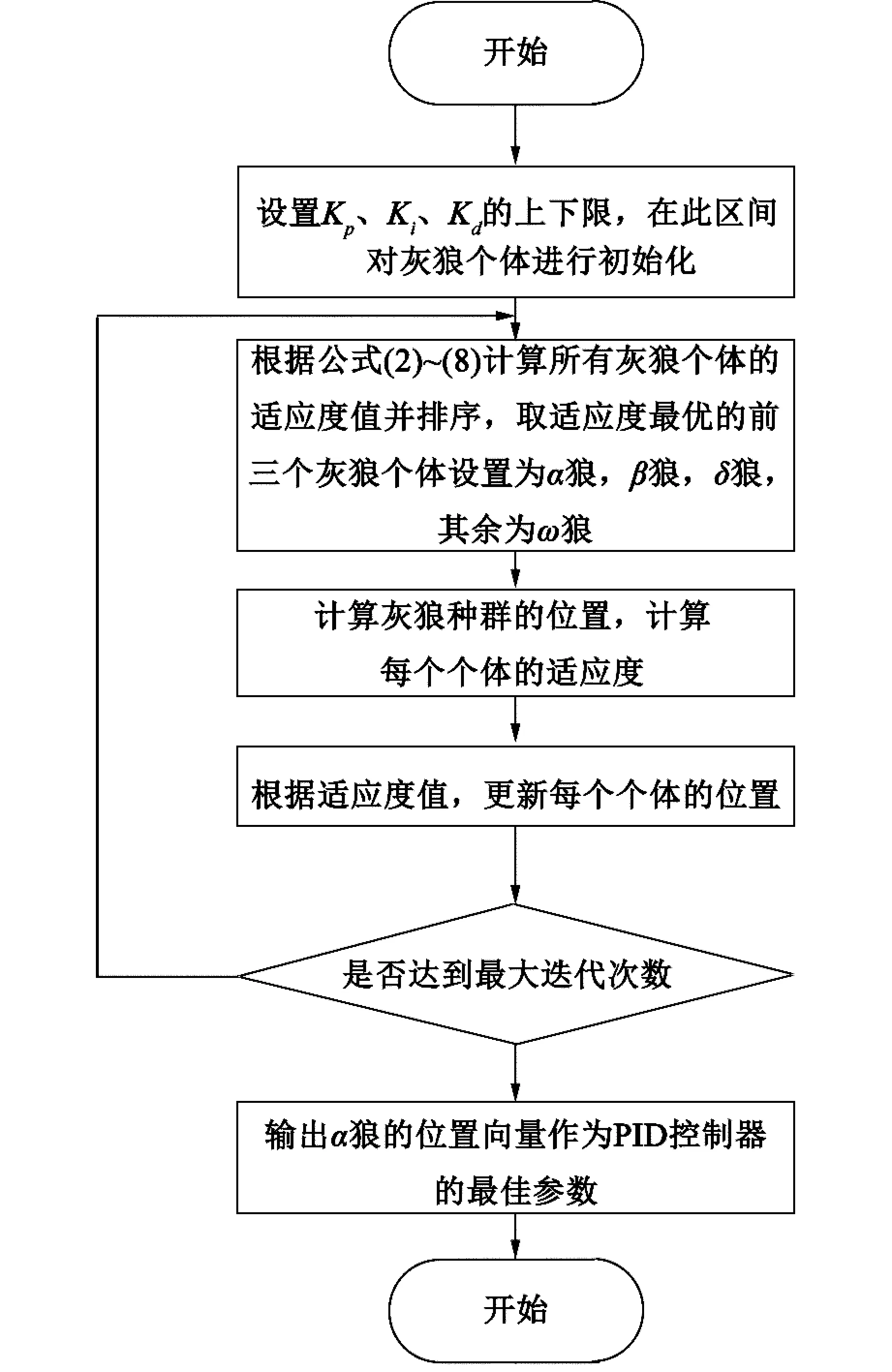
图3 灰狼优化算法流程
3 仿真验证与结果分析
3.1 参数设置
利用MATLAB R2020b软件进行仿真分析,GWO算法的种群规模设为N=30,最大迭代次数为100。各统计数据运行测试20次,取平均值。限定Kp,Ki,Kd范围均为[0,50]。
3.2 仿真结果与分析
3.2.1 基准测试函数分析
考虑篇幅限制,选用6个单峰基础测试函数和2个多峰基础测试函数测试GWO算法的收敛速度和精度。测试结果表明:在求解能力方面,灰狼算法具有全局寻优能力和收敛速度较快的优点。此外,灰狼算法采用的是自然界中灰狼群体行为的模拟,不需要对问题的先验知识,适用性较强。从算法的稳定性和鲁棒性来看,灰狼算法表现良好。在实验中,灰狼算法在不同的初值和参数设置下均能得到较好的控制效果,表明该算法具有较强的稳定性和鲁棒性。
3.2.2 GWO-PID焦炉温度控制测试
为了验证基于灰狼优化算法的有效性和优越性,在某焦化厂的实验焦炉上进行了实验评价。
实验过程中,首先搭建了焦炉温度控制系统,如图4所示。包括传感器、执行机构、控制器等硬件设备,并编写了基于MATLAB的控制系统模型。然后,利用灰狼优化算法对PID控制器参数进行优化,经过灰狼优化算法优化的PID在第10代附近就找到了最优的PID参数,系统响应时间也非常快,超调量基本很小,如图5~8所示。
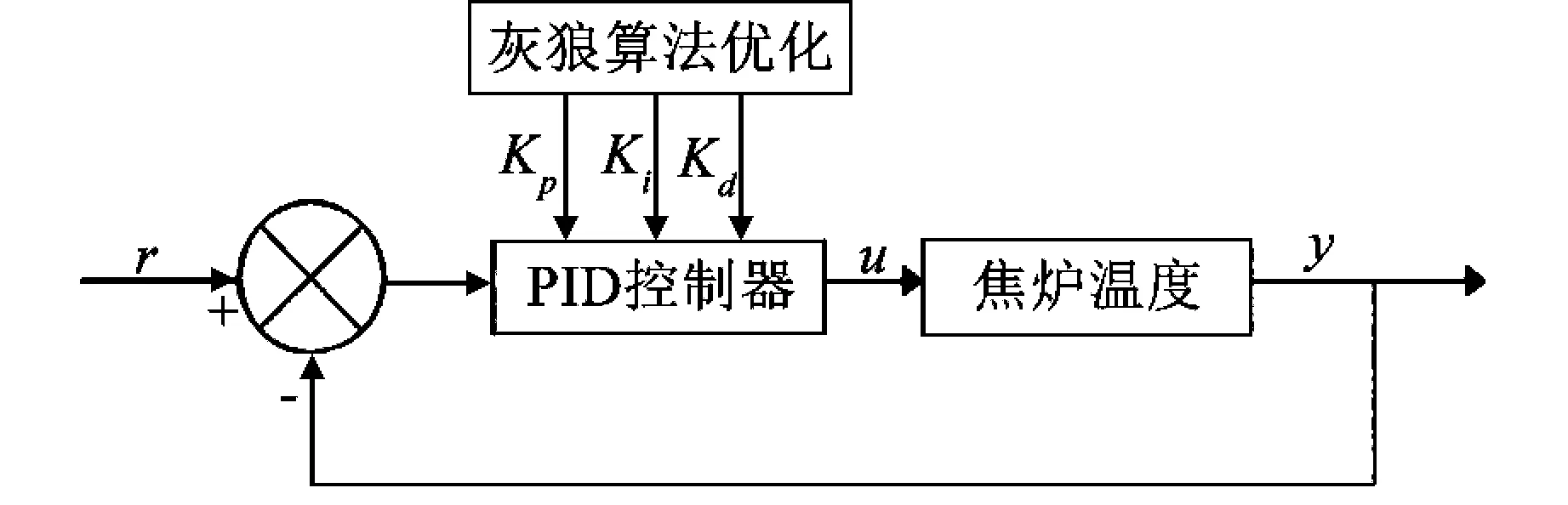
图4 基于灰狼算法的实验焦炉温度PID控制
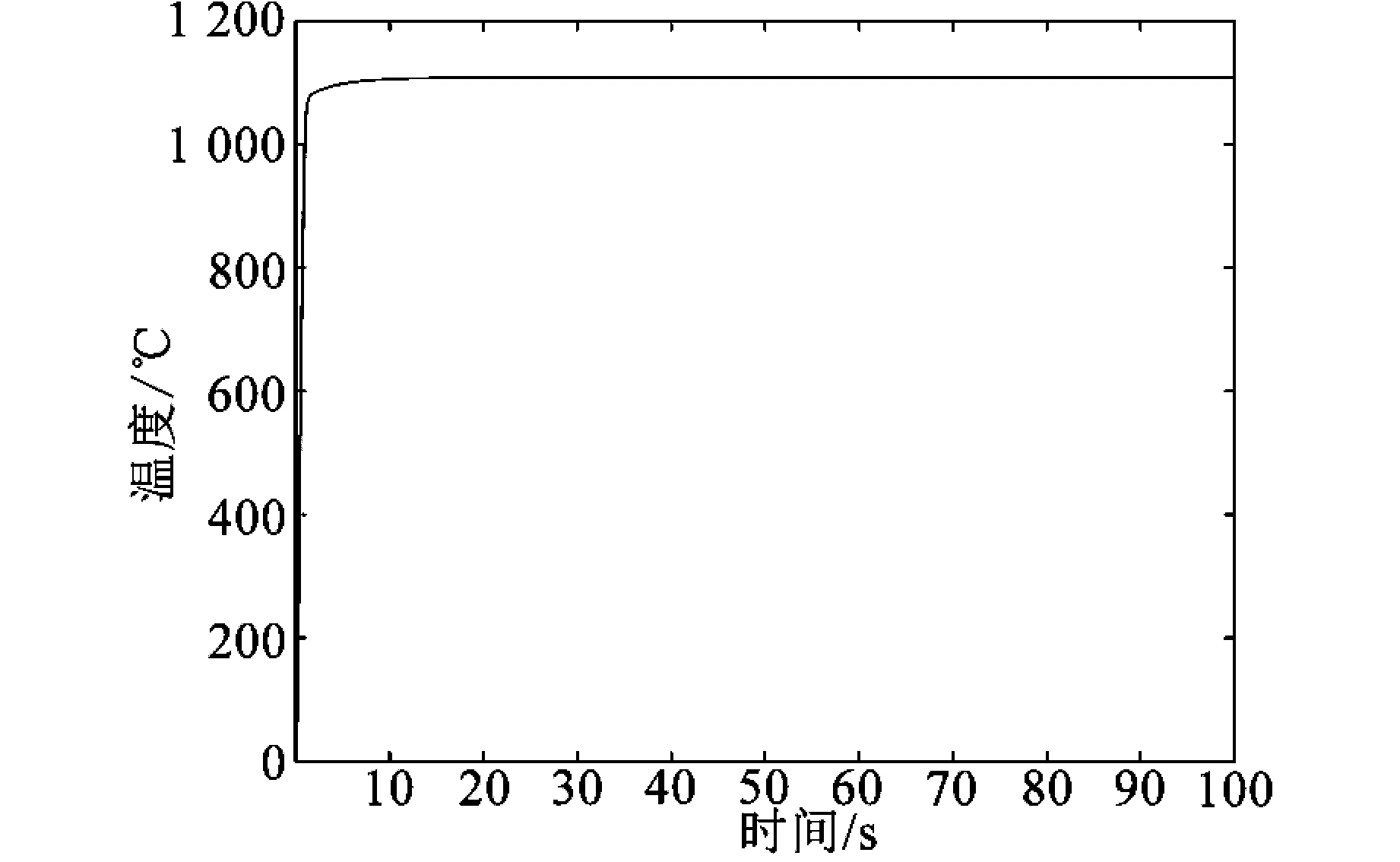
图5 基于GWO-PID的焦炉温度响应曲线
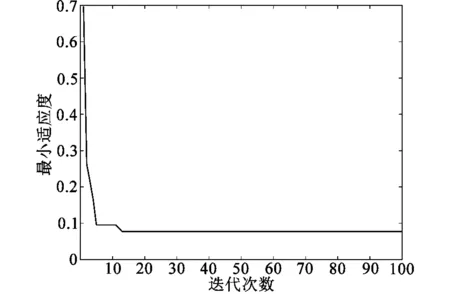
图6 最小适应度函数随迭代次数变化趋势
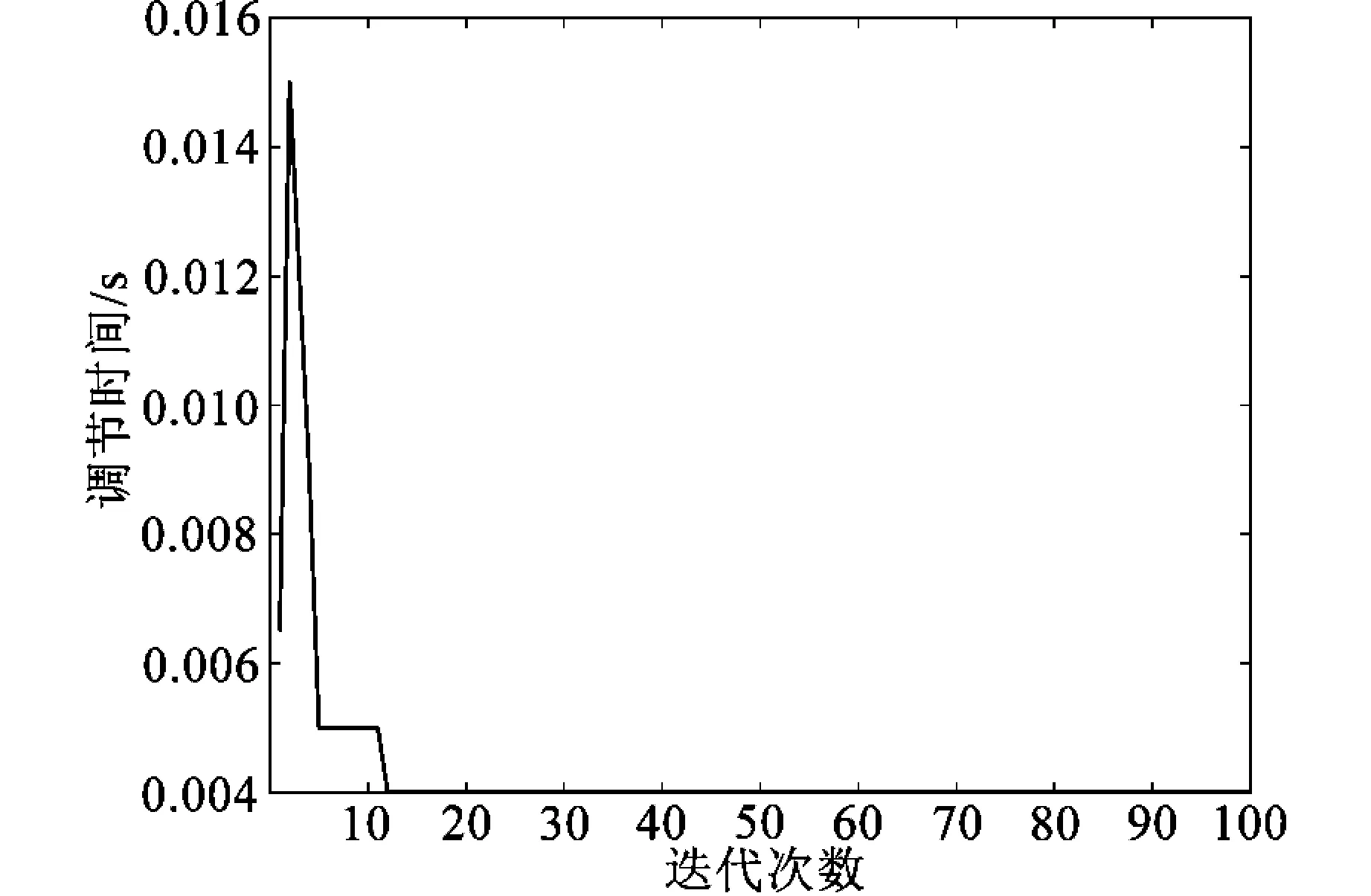
图7 调节时间随迭代次数变化趋势
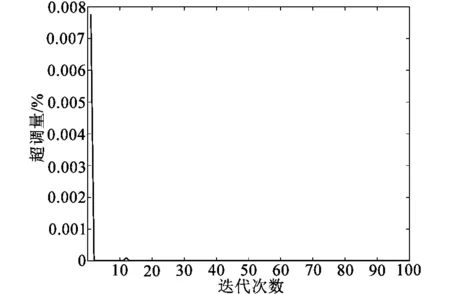
图8 超调量随迭代次数变化趋势
传统PID和GWO-PID两种算法结果对比见表1,结果表明灰狼优化算法可以有效地提高PID控制器的控制精度和响应速度。
4 结论
文章研究灰狼优化算法在实验焦炉温度控制中优化PID参数的应用。根据实验数据建立了一个简单的二阶带有纯滞后的数学模型,该模型能够反映实验焦炉的温度变化。使用灰狼算法自动优化PID控制器的参数,优化的PID控制器应用于实验焦炉的温度控制,并将结果与传统PID控制器进行比较。结果表明,相比于传统的PID算法,灰狼优化算法在优化PID控制器参数中取得了更优的性能指标,包括更短的调整时间和更小的超调量。灰狼优化算法在优化PID参数时不仅克服了传统优化算法易陷入局部最优解的缺点,而且表现出更好的全局收敛能力。
