某水利枢纽工程边坡危岩体敏感性分析

邓剑峰

(广东西江建设发展有限公司，广东 肇庆 526070)

1 工程概况

水库枢纽工程主要包括大坝、溢洪道、放水洞及电站等。坝型为黏土心墙砂壳坝，全长1200 m，顶宽7.5 m，坝高26.7 m。水库溢洪闸于1966年建成，弧形钢闸门，尺寸为10.0 m×8.0 m，共4扇，闸底板高程146.0 m，设计最大泄流量2773 m3/s。水电站建于1976年，装机3台容量600 kW，设计流量27.9 m3/s。在坝址区附近，河床向右岸侵蚀，沿岸边坡形成危岩体[1]。

2 危岩体的敏感因子权重

基于层次分析法确定水利枢纽边坡危岩体的敏感因子权重，其判断矩阵(A)如式(1)所示。

(1)

式中：A为判断矩阵；aij为对比分析标度。其判断标准如表1所示。

表1 对比分析标度及其含义

根据上述判断矩阵及对比分析标度，可计算得出影响不同破坏类型水利枢纽边坡危岩体的敏感因子权重，其计算结果如表2所示。由表可知，不同破坏类型的边坡危岩的敏感因子权重具有一致性，其中，危岩密度因子的权重最大，不同破坏形式的因子评价值为0.302，该因素的变化对于水利枢纽边坡危岩体的影响较大；地震烈度因子的权重最小，不同破坏形式的因子评价值为0.027，该因素的变化对于水利枢纽边坡危岩体的影响较小。危岩密度、风化程度及危岩自重的因子权重占总因子权重的60 %以上，以上因素为影响水利枢纽边坡危岩体的主要因素，在实际工程中，需要重点关注以上因素对水利枢纽边坡危岩体安全性的影响[2-3]。

表2 边坡危岩体敏感因子

3 危岩体数值模拟分析

3.1 滑移式危岩体分析

为验证采用层次分析法对水利枢纽边坡滑移式危岩体进行敏感性分析的可行性，采用有限元软件对水利枢纽滑移式危岩体的最大位移进行分析(模型图见图1)，以验证层次分析法的准确性，分别选取9处边坡危岩体进行分析，滑移式危岩体相关参数如表3所示。

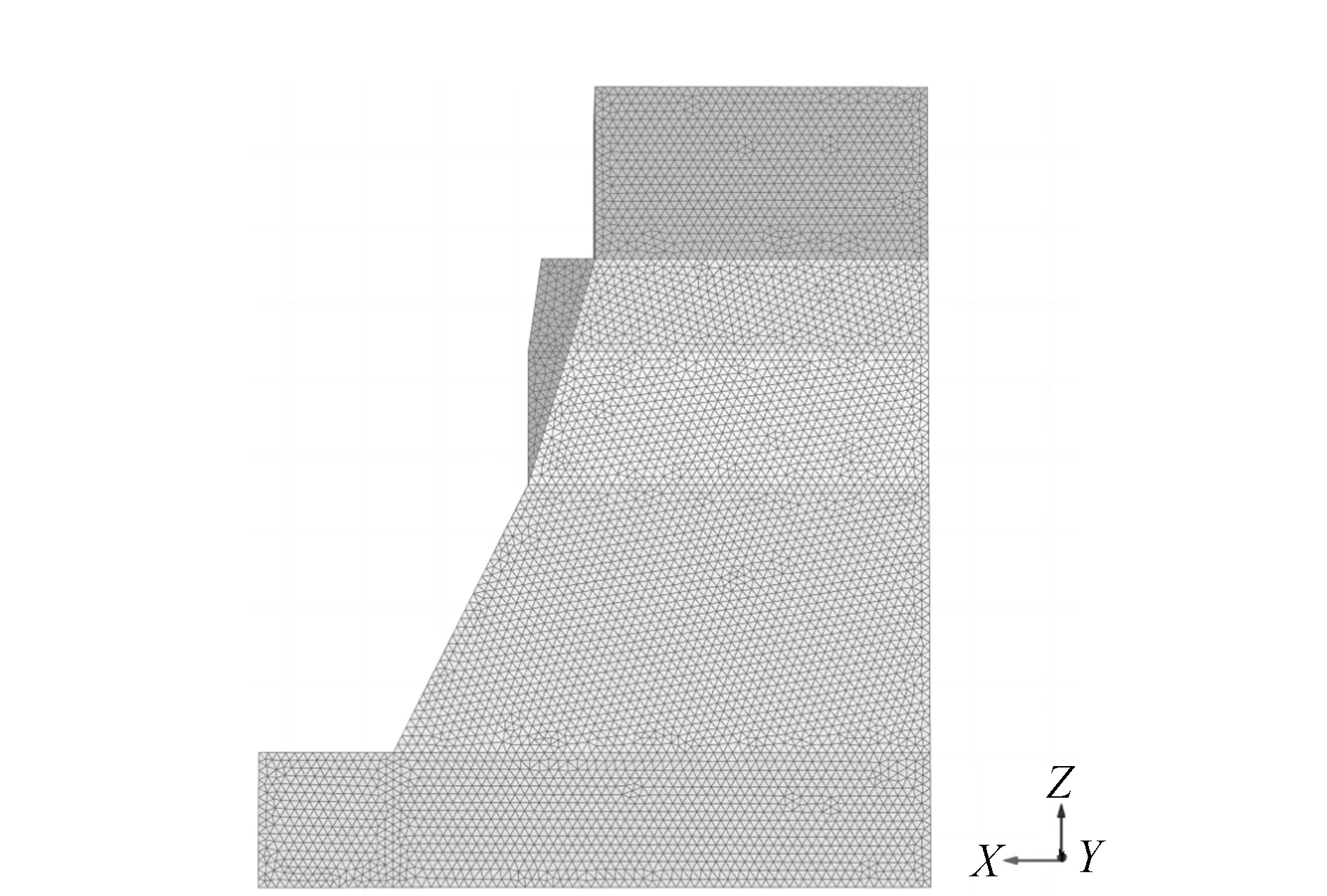
图1 数值模型

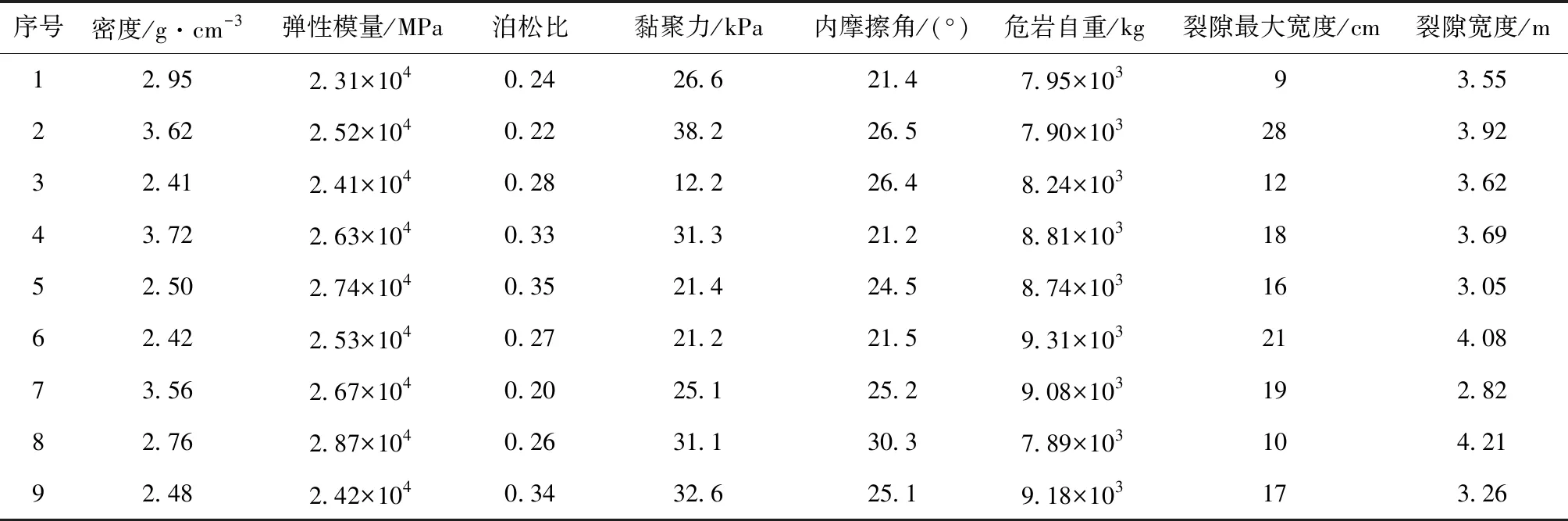
表3 滑移式危岩体相关参数

根据上述边坡危岩体参数，计算得出水利枢纽边坡危岩体不同参数的最大位移如图2所示。由图可知，不同边坡危岩体的最大位移具有一定的差异性，其中，边坡危岩体6的最大位移有最大值，其值为42.24 cm，边坡危岩体4的最大位移有最小值，其值为26.07 cm，二者间的最大位移差距为16.17 cm，说明不同参数的边坡危岩体的位移量具有一定的差异性。边坡危岩体3与边坡危岩体9间的黏聚力差距较大，其差值为20.4 kPa，但是二者间的最大位移差距较小，仅为6.89 cm，说明黏聚力对水利枢纽边坡危岩体最大位移的影响较小。根据表3可知，边坡危岩体6的危岩自重最大，说明危岩自重对水利枢纽边坡危岩体的最大位移影响较大，对比表2所示的边坡危岩体敏感因子权重可得，滑移式危岩体危岩自重的敏感因子为0.162，其数值较大，该因素对水利枢纽边坡危岩体的影响较大；表2所示的黏聚力的敏感因子为0.046，其数值较小，该因素对水利枢纽边坡危岩体的影响较小，数值模拟的结果与层次分析法结果一致，采用层次分析法对水利枢纽边坡滑移式危岩体分析的准确性较高，可应用于实际工程中。

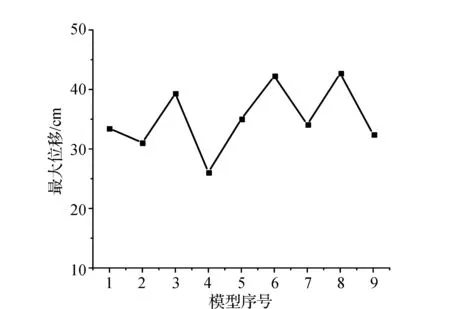
图2 滑移式危岩体最大位移曲线

3.2 坠落式危岩体分析

为验证采用层次分析法的可行性，采用有限元软件对水利枢纽坠落式危岩体的最大位移进行分析，分别选取9处坠落式危岩体进行分析，坠落式危岩体相关参数如表4所示。

表4 坠落式危岩体相关参数

根据上述坠落式危岩体模型参数，计算得出水利枢纽边坡坠落式危岩体不同参数的最大位移如图3所示。由图可知，不同坠落式危岩体的最大位移在25 ～ 45 cm间，其波动范围较大，其中，边坡危岩体8的最大位移有最大值，其值为42.69 cm，边坡危岩体4的最大位移有最小值，其值为26.11 cm，二者间的最大位移差距为16.58 cm，说明不同模型参数的危岩体的最大位移具有一定的差异性，当相关因素发生变化时，危岩体的最大位移也随之变化。由表4可得，边坡危岩体7的危岩体危岩自重最大，大于边坡危岩体8，但是其最大位移小于边坡危岩体8，说明危岩自重不是影响危岩体最大位移的最主要因素，对比滑移式危岩体可得，危岩自重对滑移式危岩体位移的影响程度大于坠落式危岩体，滑移式危岩体危岩自重的影响因子权重为0.162，坠落式危岩体危岩自重的影响因子权重为0.147，滑移式危岩体危岩自重的因子权重大于坠落式危岩体危岩自重的因子权重，危岩自重对滑移式危岩体的影响较大，数值模拟结果与层次分析法的结果一致，采用层次分析法的准确性较高。

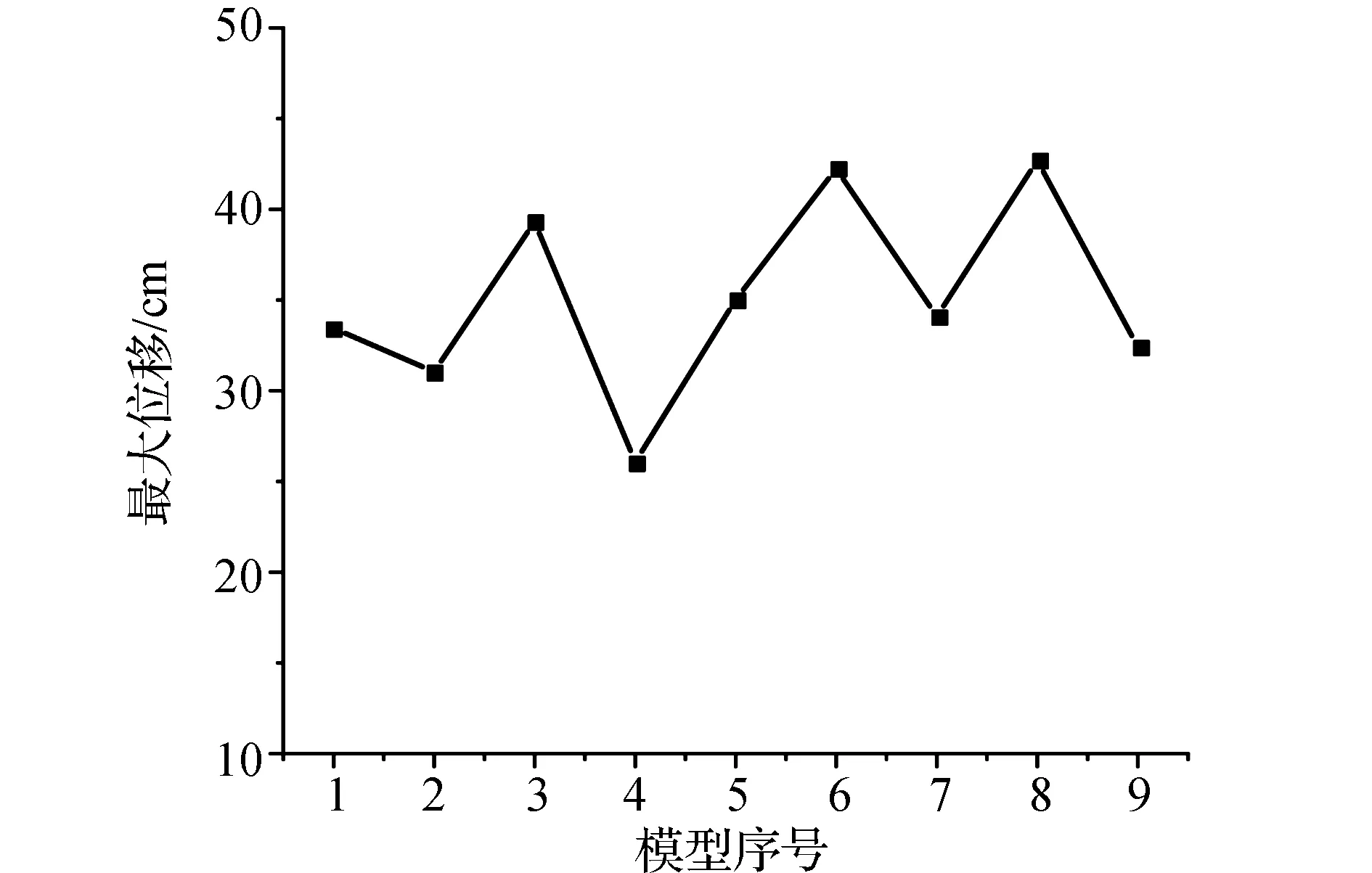
图3 坠落式危岩体最大位移曲线

3.3 倾倒式危岩体分析

为验证采用层次分析法的可行性，分析不同模型参数的水利枢纽倾倒式危岩体的最大位移，分别选取9处倾倒式危岩体进行分析，倾倒式危岩体相关参数如表5所示。

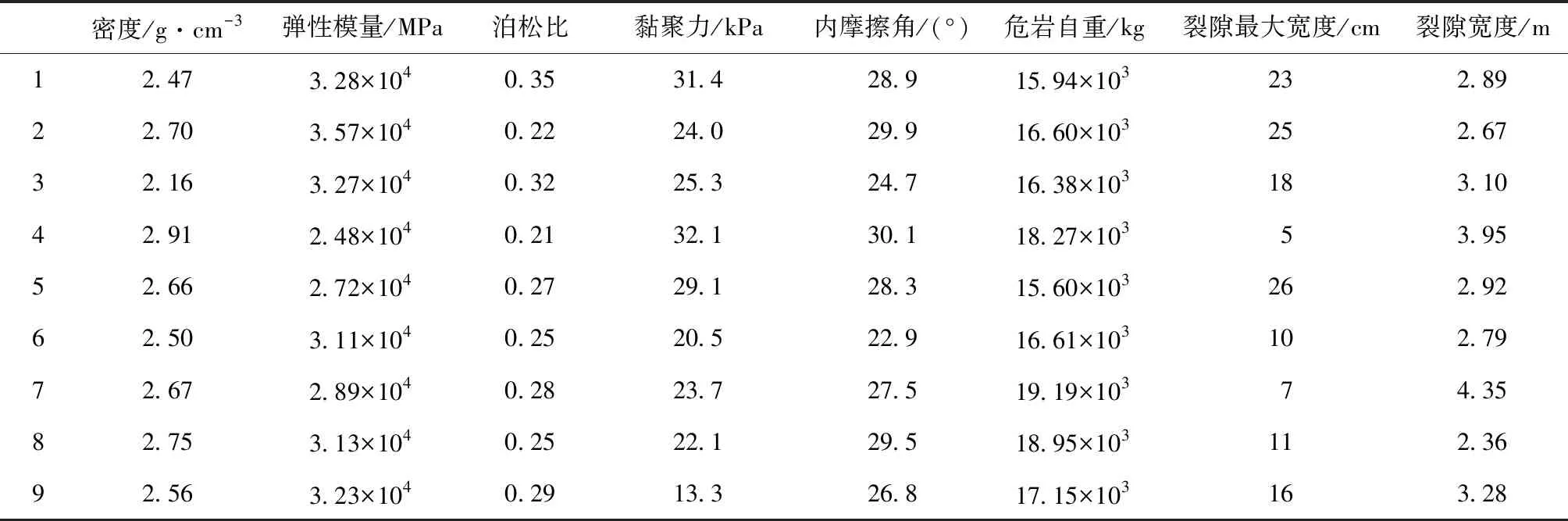
表5 倾倒式危岩体相关参数

根据上述倾倒式危岩体模型参数，计算得出水利枢纽边坡倾倒式危岩体不同参数的最大位移如图4所示。由图可知，倾倒式危岩体的最大位移与以上两种危岩体的最大位移值较为接近，其最大位移波动范围在25～45 cm间，其中，边坡危岩体8的最大位移有最大值，其值为42.91 cm，边坡危岩体4的最大位移有最小值，其值为26.15 cm，二者间的最大位移差距为16.76 cm。根据表5可得，边坡危岩体1和边坡危岩体9对应的黏聚力差距最大，其差值为18.1 kPa，但是二者间的最大位移差距较小，仅为1.02 cm，表明黏聚力的变化对于倾倒式危岩体的影响较小；倾倒式危岩体黏聚力的权重因子仅为0.044，该因素对倾倒式危岩体的影响较小，与数值模拟结果一致[4-6]。

图4 倾倒式危岩体最大位移曲线

4 结 论

本文以某水利枢纽工程边坡为背景，基于层次分析法开展敏感性分析，并利用有限元软件验证层次分析法的准确性，结果显示危岩密度因子对水利枢纽边坡危岩体的影响较大；地震烈度因子对水利枢纽边坡危岩体的影响相对较小；危岩密度、风化程度及危岩自重的因子权重占总因子权重的60 %以上，为影响水利枢纽边坡危岩体的主要因素，应当重点关注；数值模拟的结果与层次分析法结果一致，采用层次分析法对水利枢纽边坡滑移式危岩体分析的准确性较高。本文仅通过研究项目进行分析，结果具有一定的局限性，不同工程边坡地质环境差异较大，在应用中，需要进一步的分析验证。