引入扰动补偿的多电机滑模协同控制研究

安小宇，杨洋，李楠，李刚，时安琪

引入扰动补偿的多电机滑模协同控制研究

安小宇1，杨洋1，李楠2，李刚2，时安琪2

（1.郑州轻工业大学 电气信息工程学院，郑州 450002； 2.中铁工程装备集团盾构制造有限公司，郑州 450016）

解决多电机协同控制时容易受到非线性和外界扰动等不定因素的影响。基于多电机偏差耦合控制结构，与引入扰动补偿的混合非奇异终端滑模变结构控制相结合，并与传统PI（Proportional Integral）调节器控制效果做仿真对比。本文所提控制算法通过计算机仿真软件进行验证分析，该算法能够使得电机在启动时效果较好，转速误差在受到扰动时效果优于传统PI控制约8.50%；电机转矩在受到扰动后控制效果更加理想，几乎不存在迟滞时间就能达到新的负载转矩值；在受到负载扰动时转速误差波动较小，优于传统PI控制约8.83%。通过计算机仿真验证得出，引入扰动补偿后的混合非奇异终端滑模变结构控制系统的响应时间和收敛速度、控制性能和鲁棒性都要优于传统PI控制的。

多电机协同控制；偏差耦合；混合非奇异终端滑模控制

现代工业发展日新月异，多电机或电机群之间的协同控制得到重视，在包装生产、纺织、印染、智能机器人等领域应用的更加广泛[1]。多电机在要求高精度、高转速并且对产品质量高要求的系统中尤为重要。多电机的控制效果对生产质量和工程安全有决定性作用[2-3]。因此，多电机的协同控制一直是相关领域研究者们关注的课题[4]。

随着智能算法的深入研究，很多研究者将智能算法加入多电机协同控制策略中，用于优化系统的控制精度、收敛速度和鲁棒性等系统性能。王波等[5]提出了基于神经网络智能算法和PID（Proportional Integral Derivative）结合的控制方法，该方法在一定程度上减小了电机之间的同步误差，但是在前期数据不充分的情况下，无法实现神经网络对系统的自我学习。张小平等[6]设计了一种在系统运行中能够实时接收电机转矩反馈，利用模糊算法调节电机运行状态的控制系统，但是模糊规则较为简单，这使得反馈的信号不全，系统动态跟踪能力、控制精度等性能降低。

滑模变结构控制本质是非线性不连续的控制方式，控制结构不固定，随着系统状态变化而变化[7-8]，很多学者对此做了大量研究。Gao等[9]结合快速终端滑模面和非线性比例积分滑模面各自的优势，提出了一种新型的分层滑模控制。朱庆华等[10]舍弃传统滑模函数中的符号函数，设计了一种新型的动态趋近率和切换函数，很好地抑制了系统抖振。潘峰等[11]设计出双滑模直接转矩的控制方法，使得电机的转矩脉动减小，由此控制系统的抗干扰性和鲁棒性得到较大提升。

以上研究无法同时改善系统的动态性能和抑制抖振。为了实现多电机在协同控制过程中保证良好的跟踪性和同步性，本文基于滑模控制理论和多电机偏差耦合控制结构，提出引入扰动补偿的混合非奇异终端滑模变结构控制策略[12-13]。设计的扩展滑模抗扰动观测器会实时观测系统存在的扰动，及时提供足够的给定电流来抑制电机之间出现的转速变化，进行转速的前馈补偿。这样不仅提高系统趋近滑模面的速度和精度，而且很好地抑制滑模控制固有的抖振现象。为了证明本文所提出控制方法的优越性，在Matlab仿真平台将本文所提出的控制方法与传统PI（Proportional Integral）调节器控制进行仿真对比。

1 多电机协同控制策略

1.1 同步误差补偿器设计

本文的多电机控制系统是以偏差耦合控制结构为框架，现以电机1的速度误差补偿器为例，其结构如图2所示。

因为机械时间常数远大于电磁时间常数，所以转速环的响应速度相较于电流环来说明显更慢[14]。所以干扰补偿信号不经过速度环，而是反馈到电流环并直接作用到多电机系统的每个单元，从而确保系统具有更快的响应速度和跟踪能力，降低了不同电机之间差动振荡的概率[15]。

图1 四电机偏差耦合控制结构

图2 电机同步误差补偿器原理结构

当电机负载出现扰动发生变化时，采用PI控制器取代传统速度补偿器，以动态的补偿增益代替传统设置的补偿增益，达到可快速收敛电机之间的转速误差的目的，改善系统的动态性能。设计同步误差补偿器的基本思想：电机运行过程中电机之间出现速度偏差造成差速运行时，各电机的转速会由PI控制器调整后积分输出，输出数值作用于电流环，可将其作为差速电机的输入补偿，这样就形成了电机之间转速和误差跟踪信号的互联，使得整个系统具有良好的协同控制性能。

1.2 滑模速度控制器设计

非奇异终端滑模控制策略有良好的动态响应速度，系统状态变量与滑模面越接近，收敛速度越快[16]。为了提升非奇异终端滑模控制策略的快速收敛，采用混合非奇异终端滑模速度控制（Hybrid Nonsingular Terminal Sliding Mode，HNTSM）策略实现PMSM控制系统控制。这种方法解决了非奇异终端滑模控制中状态变量距滑模切换面越远时动态响应速度越慢的问题，使得动态系统具有较快的收敛速度。

1.3 混合非奇异终端滑模速度控制器设计

1.3.1 滑模面设计

由PMSM数学模型可知，PMSM运动方程为：

定义系统变量为：

再对系统状态变量求导：

因此，混合非奇异终端滑模面为：

1.3.2 求取趋近率

考虑本文实际系统趋近的运动品质，本文选取指数趋近率，表达式见式（5）。

式中：>0>0

由式（6）可知，指数项中参数影响着系统趋近滑模面的速度，值越大，移动点的趋近速度越快。当移动点接近滑面时（即()=0），指数项数值无限接近0，此时，恒定速度项的参数代替参数发挥主要作用，值越大，移动点就越快接近滑模面。

根据式（4）和式（5）求得滑模控制器输出q1为：

为验证混合非奇异终端滑模速度控制器的稳定性，选取李雅普诺夫函数为：

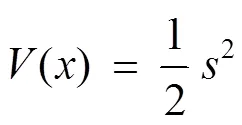
根据Lyapunov稳定性理论可知，系统变量均在有效时间内达到滑模切面，且运动稳定。

1.4 扩展滑模抗扰动观测器的设计

在复杂环境中系统会受到各种扰动，如果不能对这些扰动进行有效抑制，会使系统性能降低。因此提出一种扩展滑模扰动观测器进行前馈补偿，能够实时在线估计系统扰动。

由PMSM的动态方程可知：

在考虑电机内部参数变化和外部扰动的情况下，式（9）可以表达为式（10）。

式中：()为系统的扰动总和；∆、∆、∆为参数变化量；nnn为常规参数变量，并满足：

假设系统的扰动总和满足以下限制：

式中：为系统扰动限定值。

将系统的扰动总和()代入式（9）作为新的扩展变量，得到PMSM的扩展动态方程：

式中：()为系统扰动量总和()的变化率。

综合上各式可构建扩展滑模扰动观测器如下：

其中开关函数sm表达式见式（13）。

本文所构建的扩展模块扰动观测器的原理如图3所示。

图3 扩展滑模扰动观测器原理

式（12）减去扩展状态式（11）可得误差方程：

1.5 关于扩展模块的抖振问题分析

滑模变结构控制最大优点是具有良好的鲁棒性。滑模控制系统在运行过程中不受外界参数变化的影响，但在系统变量趋近稳定的过程中，会避免不了发生抖振，无论采取何种方法只能减弱抖振，而无法消除。

在文中为了研究抖振问题，将扰动估计误差改写成式（15）形式。

式中：为抖振信号。将式（15）代入到式（14）可得到式（16）。

可得观测误差2的传递函数见式（17）。

由式（17）可知，该传递函数与低通滤波器的作用相同，能够有效抑制高频信号，截止信号为：

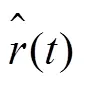
图4 抑制扰动抖振原理

2 仿真结果分析

2.1 电机参数

为了验证验证本文提出的引入扰动的HNTSM控制方法的可行性，以4台型号相同的伺服电机作为被控对象，使用Matlab仿真平台进行仿真验证。电机具体参数如表1所示。

表1 电机参数

Tab.1 Motor parameters

2.2 四电机系统仿真

设计一组4台电机控制系统，采用偏差耦合控制结构的同时选取引入扰动补偿滑模控制方法，并加入扰动观测器。空载启动后，在系统运行到0.45 s时突加3 N的额定负载，仿真波形如图6所示。

由图6可知，传统的PI控制电机启动后到达额定转速大约需要0.1 s，此时具有较大的超调量并需要一定时间调整到额定值。当在0.5 s突加负载时，转速变化量最大为250 r/min，转速降低约12.5%，恢复所需时间约0.06 s；突加负载后，电机负载转矩需要约0.02 s追踪到变化后的实际负载转矩，在0.5 s负载转矩从约2 N·m变化到约10 N·m。电机启动时的同步误差范围在±100 r/min之间，在突加负载时，同步转速误差在±17 r/min之间。在传统结构中，同步误差的调节时间约为0.07 s。电机在启动时的电流很大，可能致使电机输入电压骤降，使得电机启动转矩减小。

由图7可知，引入扰动补偿的HNTSM速度控制器后，电机由空载启动达到2 000 r/min时需要约0.1 s，启动时启动电流较小。在0.5 s突加负载时，转速变化量最大为20 r/min，转速降低约4%，恢复额定转速所需时间约为0.02 s；突加负载后，扰动观测器极快地追踪并调整到电机的实际负载转矩，转矩从2 N·m变化到10 N·m，几乎不存在迟滞时间。引入扰动补偿的HNTSM速度控制电机启动时同步误差在±1.5 r/min之间，0.5 s时突加负载扰动，同步转速误差在±1.5 r/min之间，同步误差调节时间约为0.05 s。

图5 传统PI控制的四电机性能曲线

图6 引入扰动补偿的HNTSM控制的四电机性能曲线

3 结语

本文设计的偏差耦合控制结构适用于3台及以上，对协同控制性能要求较高的多电机协同控制。该控制方法的验证仅限于仿真，仿真结果表明：启动时引入扰动补偿的HNTSM速度控制响应时间较快，几乎没有超调量；电机转矩在受到扰动后引入扰动补偿的HNTSM控制效果更加理想，起动转矩更小，几乎不存在迟滞时间就能够追踪到变化后的实际负载转矩；另外引入扰动补偿后控制方法在启动时各电机之间的同步误差更小，在受到负载扰动时上下波动区间更小。引入扰动补偿后的HNTSM速度控制可以明显提高系统的响应速度，通过补偿扰动带来的参数变化，在加快滑模面趋近速度的同时削弱了系统的抖振，因此动态性能和鲁棒性更好。

[1] 王珏, 金涛涛, 张军. 基于超扭曲非奇异滑模的多电机协调控制[J]. 科学技术与工程, 2020, 20(8): 3257-3262.

WANG Jue, JIN Tao-tao, ZHANG Jun. Multi-Motor Coordination Control Based on Super-Twisting Nonsingular Sliding Mode[J]. Science Technology and Engineering, 2020, 20(8): 3257-3262.

[2] CHEN Zhi-hua, HE Juan-juan, ZHENG Ying, et al. An Optimized Feedforward Decoupling PD Register Control Method of Roll-to-Roll Web Printing Systems[J]. IEEE Transactions on Automation Science and Engineering, 2015, 13(1): 1-10.

[3] 彭晓燕, 刘威, 张强. 基于改进型偏差耦合结构的多电机同步控制[J]. 湖南大学学报(自然科学版), 2013, 40(11): 77-83.

PENG Xiao-yan, LIU Wei, ZHANG Qiang. Synchronized Control of Multi-Motor Based on the Improved Relative Coupling Control[J]. Journal of Hunan University (Natural Sciences), 2013, 40(11): 77-83.

[4] 高振新, 孙建红. 多电机无轴传动同步控制策略[J]. 包装工程, 2016, 37(15): 144-149.

GAO Zhen-xin, SUN Jian-hong. Multi-Motor Synchronization Control Strategy with Shaftless Drive[J]. Packaging Engineering, 2016, 37(15): 144-149.

[5] 王波, 曹春平, 胥小勇, 等. 基于神经网络的流涎机组多电机同步控制研究[J]. 中国机械工程, 2014, 25(1): 46-50.

WANG Bo, CAO Chun-ping, XU Xiao-yong, et al. Research on Multi-Motor Synchronization of Salivation Unit Based on Neural Network[J]. China Mechanical Engineering, 2014, 25(1): 46-50.

[6] 张小平, 李震广, 张铸. 基于模糊控制双开关磁阻电机同步控制方法[J]. 控制工程, 2017, 24(11): 2356-2361.

ZHANG Xiao-ping, LI Zhen-guang, ZHANG Zhu. A Synchronic Control Method for Double Switched Reluctance Motors Based on Fuzzy Control[J]. Control Engineering of China, 2017, 24(11): 2356-2361.

[7] 张立伟, 李行, 宋佩佩, 等. 基于新型滑模观测器的永磁同步电机无传感器矢量控制系统[J]. 电工技术学报, 2019, 34(S1): 70-78.

ZHANG Li-wei, LI N, SONG Pei-pei, et al. Sensorless Vector Control Using a New Sliding Mode Observer for Permanent Magnet Synchronous Motor Speed Control System[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 70-78.

[8] GAO Y, ZHAO H, MA K, et al. Control Design for Current Loop of PMSM Using a Modified Model Compensation ADRC Controller[C]// 2020 39th Chinese Control Conference (CCC), IEEE, 2020: 2540-2550.

[9] GAO P, ZHANG G M, CAO J, et al. A Novel Hierarchical Nonlinear Proportional-Integral Fast Terminal Sliding Mode Control For PMSM Drives[J]. Advances in Mechanical Engineering, 2021, 13(4): 1-13.

[10] 朱庆华, 董瑞琦, 马广富. 基于动态滑模控制的挠性航天器姿态控制[J]. 控制理论与应用, 2018, 35(10): 1430-1435.

ZHU Qing-hua, DONG Rui-qi, MA Guang-fu. Dynamical Sliding Mode for Flexible Spacecraft Attitude Control[J]. Control Theory & Applications, 2018, 35(10): 1430-1435.

[11] 潘峰, 闫庚龙, 苑伟华, 等. 基于双滑模的永磁同步电机直接转矩控制[J]. 电工技术学报, 2018, 33(S2): 427-433.

PAN Feng, YAN Geng-long, YUAN Wei-hua, et al. Research on Direct Torque Control for Permanent Magnet Synchronous Motor Based on the Double Sliding Mode[J]. Transactions of China Electrotechnical Society, 2018, 33(S2): 427-433.

[12] 张慧柔. 引入扰动补偿的永磁同步电机滑模速度控制策略研究[D]. 西安: 西安理工大学, 2020: 6-30.

ZHANG Hui-rou. Research on Sliding Mode Speed Control Strategy of Permanent Magnet Synchronous Motor with Disturbance Compensation[D]. Xi'an: Xi'an University of Technology, 2020: 6-30.

[13] 李慧, 刘星桥, 李景, 等. 多电机同步协调系统控制策略[J]. 电机与控制应用, 2014, 41(4): 6-11.

LI Hui, LIU Xing-qiao, LI Jing, et al. Summary of Multi-Motor Synchronization and Coordination System Control Strategy[J]. Electric Machines & Control Application, 2014, 41(4): 6-11.

[14] 夏长亮, 李莉, 谷鑫, 等. 双永磁电机系统转速同步控制[J]. 电工技术学报, 2017, 32(23): 1-8.

XIA Chang-liang, LI Li, GU Xin, et al. Speed Synchronization Control of Dual-PMSM System[J]. Transactions of China Electrotechnical Society, 2017, 32(23): 1-8.

[15] LU Zheng, WANG Zi-xin, LU Xi-lin. Nonlinear Dissipative Devices in Structural Vibration Control: A Review[J]. Journal of Sound and Vibration, 2018, 423(5): 18-49.

[16] 李春文, 赵德宗, 任军. 基于全滑模面的多感应电机速度同步控制[J]. 系统工程理论与实践, 2009, 29(10): 110-117.

LI Chun-wen, ZHAO De-zong, REN Jun. Total Sliding Mode Speed Synchronization Control of Multi Induction Motors[J]. Systems Engineering -Theory & Practice, 2009, 29(10): 110-117.

Multi-motor Sliding Mode Cooperative Control by Introducing Disturbance Compensation

AN Xiao-yu1, YANG Yang1, LI Nan2, LI Gang2, SHI An-qi2

(1. College of Electrical and Information Engineering, Zhengzhou University of Light Industry, Zhengzhou 450002, China; 2. Shield Manufacturing Co., Ltd., China Railway Engineering Equipment Group Co., Ltd., Zhengzhou 450016, China)

The work aims to solve the problem that the multi-motor cooperative control is easily affected by uncertain factors such as nonlinearity and external interference. Based on the multi-motor deviation coupling control structure, the hybrid non-singular end sliding mode with disturbance compensation was combined with the variable structure control to conduct simulation comparison with the traditional PI (Proportional Integral) regulator in terms of control effect. Focusing on the verification and analysis of the proposed control algorithm by computer simulation software, it could be concluded as follows. First, when the overall disturbance was encountered, the speed error could be improved by 8.50% compared with the traditional PI control. Specifically, when the motor torque was disturbed, the control effect was more ideal, in which the new load torque value can be reached with almost no lag time. In addition, when load disturbance occurred, the speed error fluctuation was smaller, which was improved by about 8.83% compared with traditional PI control. In general, according to verification through computer simulation, the hybrid non-singular end sliding mode variable structure control system with disturbance compensation is superior to the traditional PI control in response time, convergence speed, control performance and robustness.

multi-motor cooperative control; relative coupling; hybrid non-singular end sliding mode control

TB486；TP27

A

1001-3563(2023)15-0146-07

10.19554/j.cnki.1001-3563.2023.15.019

2022–05–23

郑州市重大科技创新专项（2020CXZX0066）

安小宇（1979—），男，硕士，副教授，主要研究方向为工业控制、先进自动化技术控制与应用等。

责任编辑：曾钰婵