巧用平均速度解决动量、能量问题

郑海燕

(新疆昌吉州第二中学)

物理学是研究物质运动的最基本、最普遍的规律及物质的构成、物质间相互作用的一门科学。自然界中物质的运动和构成及其相互作用是极其复杂的,但他们之间存在着各种各样的等同性,为了认识复杂的物理规律,我们往往从事物的等同效果出发,将其转化为简单的、易于研究的物理事物或规律,这种方法就是等效替代法。

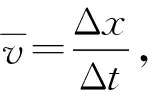
【例1】如图1甲所示,一块长度为L、质量为m的木块静止在光滑水平面上。一颗质量也为m的子弹以水平速度v0射入木块。当子弹刚射穿木块时,木块向前移动的距离为s,如图1乙所示。设子弹穿过木块的过程中受到的阻力恒定不变,子弹可视为质点。则子弹穿过木块的时间为( )

图1

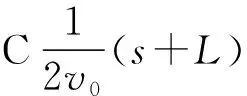
解法一：(用动量和能量的观点)

子弹穿过木块过程,子弹和木块组成的系统动量守恒,以v0的方向为正方向,有

mv0=mv1+mv2

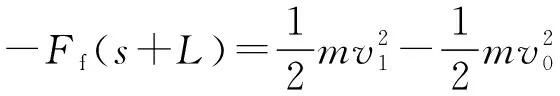
由动量定理得-Fft=mv1-mv0

由动量定理得Fft=mv2

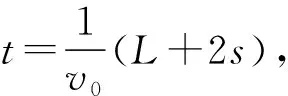
这种解法涉及4个未知数和5个方程,如果我们在草稿纸上验算,将会发现计算过程很烦琐,要得出答案很不容易,大多数学生要解很久,而且未必能得出正确结果,计算量很大,非常考验学生的耐心和运算能力。

解法二：(平均速度法)

因为阻力恒定不变,所以子弹和木块均做匀变速运动,

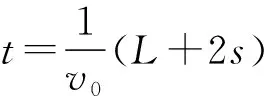
相较于解法一,平均速度法只有3个未知数和四个方程,且方程形式非常简单,表达式中无二次项,计算方便简捷,能快速解决问题,表面看是动量和能量问题,实则只用运动学公式。这种解法快又准。

【例2】如图2所示,有一质量为m1=3 kg的长木板静止在光滑的水平地面上,木板的左端有质量为m2=1 kg的物块。用水平向右的恒力F作用在物块上,一段时间后撤去恒力F,最终物块和木板的共同速度v共=2 m/s,整个过程中系统产生的热量为8 J,恒力F的冲量大小为I,撤去恒力F时木板的速度为v,则( )

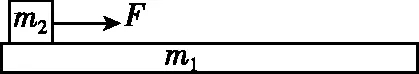
图2

A.I=8 N·s B.I=16 N·s

解法一：(图像法)如图3

对系统用动量定理I=(m1+m2)v共=8 N·s,故A正确;设在t1时刻撤去拉力F,m2的速度为v2。在t2时刻共速。

在t1～t2段,由牛顿第二定律可知-a2=3a1

所以v2-2=3×(2-v)即v2=8-3v

在0～t2,m2相对m1的位移为

Δx=(4-2v)t2

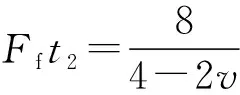
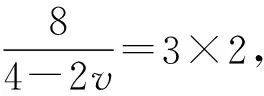
解法二：(平均速度法)

对系统用动量定理,有

I=(m1+m2)v共=8 N·s,A正确;

由能量守恒可知,拉力F的功

已知Q=8 J,得W=16 J

又因为I=Ft1;W=Fx2(x2为0～t1内m2的位移)

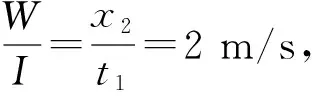
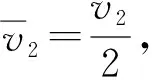
再对系统在t1～t2段用动量守恒得

m1v+m2v2=(m1+m2)v共=8 N·s

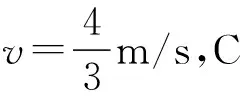
通过两种解法对比,不难看出平均速度法,思路直接,过程简捷,能以较快的速度解决问题。

【例3】(2022·全国乙卷·25)如图4,一质量为m的物块A与轻质弹簧连接,静止在光滑水平面上:物块B向A运动,t=0时与弹簧接触,到t=2t0时与弹簧分离,第一次碰撞结束,A、B的v-t图像如图5所示。已知从t=0到t=t0时间内,物块A运动的距离为0.36v0t0。A、B分离后,A滑上粗糙斜面,然后滑下,与一直在水平面上运动的B再次碰撞,之后A再次滑上斜面,达到的最高点与前一次相同。斜面倾角为θ(sinθ=0.6),与水平面光滑连接。碰撞过程中弹簧始终处于弹性限度内。求:

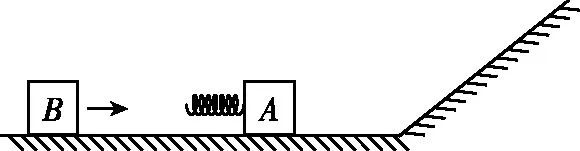
图4

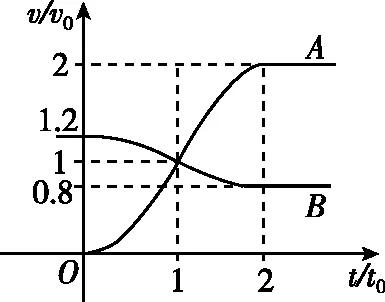
图5

(1)第一次碰撞过程中,弹簧弹性势能的最大值;

(2)第一次碰撞过程中,弹簧压缩量的最大值;

(3)物块A与斜面间的动摩擦因数。

【解析】(1)当弹簧被压缩最短时,弹簧弹性势能最大,此时A、B速度相等,即t=t0时刻,根据动量守恒定律有

mB·1.2v0=(mB+m)v0

根据能量守恒定律有

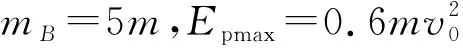
(2)解法一：(利用数学积分的思想求解)

同一时刻弹簧对A、B的弹力大小相等,根据牛顿第二定律F=ma

可知同一时刻aA=5aB

则同一时刻A、B的瞬时速度分别为

vA=aAt

根据位移等速度在时间上的累积可得

sA=vAt(累积)

sB=vBt(累积)

又sA=0.36v0t0

解得sB=1.128v0t0

第一次碰撞过程中,弹簧压缩量的最大值

Δs=sB-sA=0.768v0t0

这种方法较为抽象,如果对积分概念模糊不清就会难以理解。像这种有两个变量的积分更无从了解,也就无法切入。对数学知识的要求和数理结合能力的要求都很高。

解法二：(图像法)如图6

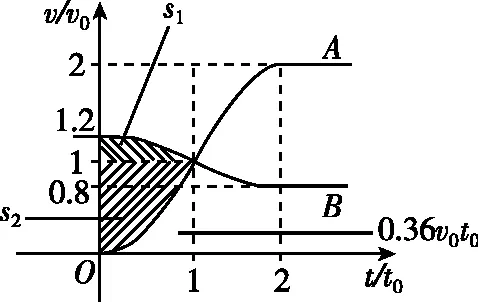
图6

图中上部阴影部分为s1,下部阴影部分为s2,最大压缩量Δs

则Δs=s1+s2

由题意和图像可知

s2=5s1

s2=v0t0-0.36v0t0=0.64v0t0

得Δs=0.768v0t0

此解题方法巧妙利用数学函数图像特点,但是也用到了积分概念,虽然抽象,切入点生疏,但总体较为容易接受,毕竟速度时间图像学生非常熟悉,已熟知图像面积表示位移大小,斜率表示加速度大小。

解法三：(平均速度法)

已知mB=5m,由系统动量守恒得

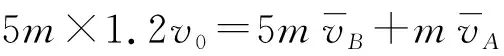
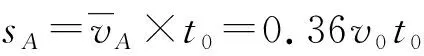
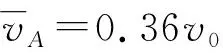
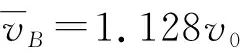
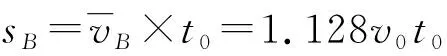
得Δs=sB-sA=0.768v0t0

这种方法最为巧妙,不偏僻,不生疏,平均速度乘以时间等于位移,这个关系学生耳熟能详,大多数学生都能掌握理解。不仅简化了运算,也简化了对物理过程的理解。

(3)物块A第二次到达斜面的最高点与第一次相同,说明物块A第二次与B分离后速度大小仍为2v0,方向水平向右,设物块A第一次滑下斜面的速度大小为vA′ ,设向左为正方向,根据动量守恒定律可得

mvA′ -5m·0.8v0=m·(-2v0)+5mvB′

根据能量守恒定律可得

联立解得vA′=v0

设在斜面上滑行的长度为L,上滑过程,根据动能定理可得

下滑过程,根据动能定理可得

联立解得μ=0.45

从以上示例可以看出在处理物体运动的问题时,借助平均速度公式,可以降二次方程为一次方程,以简化运算,极大提高运算速度和准确率。这种应用等效替换法把陌生的、复杂的物理现象或物理过程在保证效果、关系相同的前提下,转化为简单的、熟悉的物理现象、物理过程来研究,从而认识研究对象本质和规律的方法,是物理学中重要的思维方法和解题技巧。因此教师在平时的教学中应多积累不同的解题方法,以一题多解的形式呈现给学生,不仅激发学生的学习兴趣,发展思维,还对学生的思维品质、应变能力、逻辑严密性等有提升作用,以培养学生多角度、深层次思考并解决问题的能力,发展“举一反三” “因小见大” “闻一以知十”等智慧。而且通过一题多解学生对物理过程的理解更深入,才能融会贯通从中寻找到最优解题方法,对培养学生的高阶思维有着促进作用。从长远来看,未来的人才竞争就是今天的教育竞争,思考并践行先进教学理念和方法,为学生的全面发展和个性发展搭建平台,给学生提供浩瀚的思维发展空间,为学生的终身学习发展奠定坚实的基础,着力提高学生学习能力、实践能力、创新能力,是每一位教师的使命。教师应该义不容辞地直面挑战、砥砺前行。