基于多元线性逐步回归和BP 神经网络建立鸭梨盛花期预测模型

王鹏飞，李涛*，于春亮，薛敏，张玉星，张海霞，权畅，许建锋，马辉

(1.河北农业大学园艺学院，河北 保定 071000；2.威县农业农村局，河北 威县 054700；3.邯郸市气象局，河北 邯郸 056000；4.河北省气象科学研究所，河北 石家庄 050000)

梨是河北省优质水果之一，截至2021 年底，种植面积达115 466.67 公顷、产量366.6 万吨、产值140.3 亿元，均居全国第1 位。 其中鸭梨作为河北省邯郸市魏县主栽品种之一，栽培面积大，历史悠久，是当地农业的支柱产业之一，近年又通过举办“梨花节”等活动进一步助力当地乡村振兴[1]。魏县鸭梨盛花期集中在早春气温变化幅度较大的3 月下旬—4 月上旬，期间若发生“倒春寒”，不仅会造成当年梨果大量减产，也会影响“梨花节”等活动的方案制定和开展。 近20 多年来全球气候波动明显，每年观测到的气象数据和盛花期时间已明确表明气候变暖影响到了梨花期[2]，使梨花期提前，导致遭遇“倒春寒”的概率进一步增大[3，4]。 因此，利用多年连续观测的鸭梨花期资料和气象数据建立模型对鸭梨盛花期进行预测，是预防“倒春寒”和制定“梨花节”活动预告的重要前提[5]。

目前已有学者开展了花期预测模型相关研究，大多是基于气象因子与花期的相关关系进行的。 如刘璐等[6]使用偏最小二乘回归法分析明确平均气温和平均地温是影响中国北方主产地苹果始花期的最关键主导因子，进一步利用逐步回归法建立预测模型，误差小于5 天；柏秦凤等[7]对0、3、5、10℃活动/有效积温与始花期进行相关性分析，筛选出影响富士系苹果花期的气象因子，并建立了5 个主产区富士系苹果始花期预测模型；谭静[8]、冯敏玉[9]等也通过分析气象因子与花期的相关性，选出显著影响花期的气象因子，通过建立多元回归模型，分别对樱花、油菜花的花期进行预测，取得了一定成效。

近年来，随着计算机技术的快速发展，机器学习算法的使用越来越广泛，已成为现代农业气象科研和业务开展的重要工具[10]。 例如随机森林[11]、神经网络[12]、ARMA[13]等已经较好地应用于苹果[14]、小麦[15]等的花期预测。 本研究以通过相关分析筛选出的气象因子作为自变量(输入层)、盛花期日序数作为因变量(输出层)，分别利用BP 神经网络算法、多元线性逐步回归建立魏县鸭梨盛花期预测模型，经评价筛选出预测精度较高的模型，以期为预防魏县鸭梨花期“倒春寒”和保障“梨花节”等相关活动顺利开展提供技术支持。

1 数据来源与研究方法

1.1 研究区概况

魏县位于河北省邯郸市，地处河北、山东、河南三省交界处，北纬36°03′6″～36°26′30″、东经114°43′42″～115°07′24″，卫河、漳河横贯县城。 地势由西南向东北缓缓倾斜，开阔平缓，海拔45.8 ～58.5 m。 日照时数在1 855～2 373 h 之间，年平均气温为13.7℃，年降水量为333.8 ～746.2 mm。 鸭梨种植面积10 000 公顷，总产量达35 万吨。

1.2 数据来源

2002—2020 年鸭梨逐年盛花期观测资料和气象数据，分别由河北省邯郸市魏县林果开发服务中心、河北省梨气象服务中心提供。 其中，气象数据为魏县1—3 月气温、降水量、积温、日照时数等气象因子逐年数据，由河北省气象局在魏县建立的国家气象站(东经114.95°，北纬36.33°)收集；盛花期为逐年观测记录资料，以梨树植株50%以上花朵展开的日期作为盛花期标准[16]。本研究所预测的盛花期并不针对某一个梨园，而是根据魏县林果开发服务中心提供的全县鸭梨平均盛花期进行预测的。

1.3 数据处理与分析

将逐年盛花期时间转化为日序数进行统计分析，即1 月1 日为起始日，日序数为1，以此类推，2 月1 日的日序数为32。 魏县鸭梨盛花期多集中在3 月下旬—4 月上旬，为了展现预测的提前性，将选择的各类气象因子指标计算截止时间定为较历年最早盛花期(3 月23 日)早13 天的3 月10日。 选用1 月1 日—3 月10 日的逐月与逐旬平均气温、平均最高气温、平均最低气温、平均降水量、平均日照时数及≥0℃活动积温、≥3℃活动积温、≥5℃活动积温、≥10℃活动积温、≥3℃有效积温、≥5℃有效积温、≥10℃有效积温等气象因子，通过Pearson 相关性分析选出与盛花期相关性较高的气象因子用于预测模型建立，并用2021、2022 年预测结果与实际盛花期时间进行对比分析，以验证模型的预测效果。

气象因子及盛花期日序数采用Microsoft Excel 软件进行统计，气象因子与盛花期的相关性用SPSS 25 软件、Pearson 法进行分析。

1.4 基于多元线性逐步回归的建模方法

多元线性回归(MLR)主要是研究一个因变量与多个自变量之间的线性回归关系，由多个自变量的最佳组合来预测因变量，但由于自变量之间可能存在多重共线性，因此，本研究利用SPSS 25，采用逐步法，考察引入模型的自变量是否仍然具有统计学意义，以检验其是否有继续保留在方程中的价值，并以P值最小且具有统计学意义为依据进行自变量的引入和剔除。 引入自变量的显著性概率为P＜0.05，剔除自变量的显著性概率为P＞0.10。 采用方差膨胀系数(VIF)诊断自变量之间是否存在多重共线性，VIF＞10 表示存在严重的多重共线性；对回归方程进行F 检验，若F＞F0.01，则表示建立的回归方程有效。

1.5 基于BP 神经网络的建模方法

BP 神经网络由输入层、隐含层、输出层及每层之间的结点连接组成，使用梯度搜索技术并利用反向传播不断调整网络的权值和阈值，最终实现网络实际值与预测值的误差最小化[17]。 在网络设计过程中，隐含层神经元个数的确定十分重要，若隐含层节点数过多，会加大计算量并容易产生训练过度的问题；若节点数过少，则从样本中获取的信息较少，达不到较好的效果[18]。 因此，本研究根据经验公式[18]确定隐含层节点数(式中k 为输入层节点数，m 为输出层节点数，α为[1，10]之间的常数)，以通过Pearson 相关系数筛选出的与鸭梨盛花期相关显著(P＜0.01)的气象因子作为输入层节点，以盛花期作为输出层，利用Matlab 2018a，建立了3 层前馈型单隐含层BP 神经网络，用于鸭梨盛花期的预测。

1.6 模型精度评价

以实际鸭梨盛花期观测资料作为最终的预测精度验证数据，利用决定系数(R2)、均方根误差(RMSE)、预测准确率/预测误差率(Rd(1，2))对预测模型进行精度评价和误差分析。

式中，n 为盛花期年份数量，y 为实际鸭梨盛花期日序数，y＾为预测鸭梨盛花期日序数，为鸭梨盛花期日序数的均值；Rw表示预测盛花期时间与实际盛花期时间误差在±1 天和±2 天及在±3 天以上的年份数；Rz表示进行预测的总年份数；当误差在±1 天和±2 天时，计算的Rd1表示预测准确率；当误差在±3 天时，计算的Rd2表示预测误差率。

2 结果与分析

2.1 鸭梨盛花期变化特征

2002—2020 年魏县鸭梨平均盛花期日序数为90，与之对应的盛花期出现在3 月30 日(平年)或3 月31 日(闰年)。 盛花期最早出现在3月23 日(2002 年)，最晚出现在4 月8 日(2005、2012 年)，最早与最迟盛花期日序数相差16。 有12 年出现在3 月下旬，占总样本的63.15%；有7年出现在4 月上旬，占总样本的36.85%。 采用线性倾向估计法对鸭梨盛花期总体变化趋势进行分析，结果(图1)表明，2002—2020 年间，鸭梨盛花期日序数呈减少趋势，即盛花期呈提前趋势，其线性倾向率为-2.4 d/10 a。

图1 鸭梨盛花期变化趋势

2.2 影响鸭梨盛花期的气象因子筛选

2.2.1 平均气温、降水量及日照时数与盛花期的相关性 分别对1—3 月上旬逐月与逐旬的平均气温、平均最高气温、平均最低气温、平均降水量、平均日照时数等共计45 个因子进行分析，结果有16 个气象因子与盛花期的相关性通过显著检验(P＜0.05)，包括平均气温的5 个、最高气温的6个、最低气温的4 个、降水量的1 个，见表1。 其中，气温因子中，鸭梨盛花期与1 月、1 月上旬、3月上旬的平均气温和1 月上旬的平均最高气温以及1 月、1 月上旬、3 月上旬的平均最低气温呈极显著(P＜0.01)负相关关系，相关系数在-0.626 ～-0.776 之间；1 月平均降水量与盛花期也呈现极显著相关关系，相关系数为-0.575。 逐月及逐旬日照时数与盛花期未通过显著性检验，1—3 月上旬的日照时数对魏县鸭梨开花早晚无显著影响。选择通过极显著(P＜0.01)水平的气象因子作为后续建立预测模型的自变量，共8 个，分别为T1、T2、T5、T7、T12、T13、T15、T16。

表1 2002—2020 年1—3 月逐月和逐旬气象因子与盛花期的相关系数

2.2.2 积温与盛花期的相关性 对1—3 月上旬7 个活动/有效积温因子与盛花期的相关性进行Pearson 相关分析，结果(表2)表明，仅有5 个积温因子与盛花期的相关性通过0.01 水平显著检验，分别为≥0℃活动积温、≥3℃活动积温、≥5℃活动积温、≥3℃有效积温、≥5℃有效积温，用于后续建立预测模型。 其中，活动积温与盛花期之间呈现较强的负相关关系，相关系数为-0.820 ～-0.852，即≥0℃、≥3℃、≥5℃活动积温值越大，盛花期越早，反之越迟。

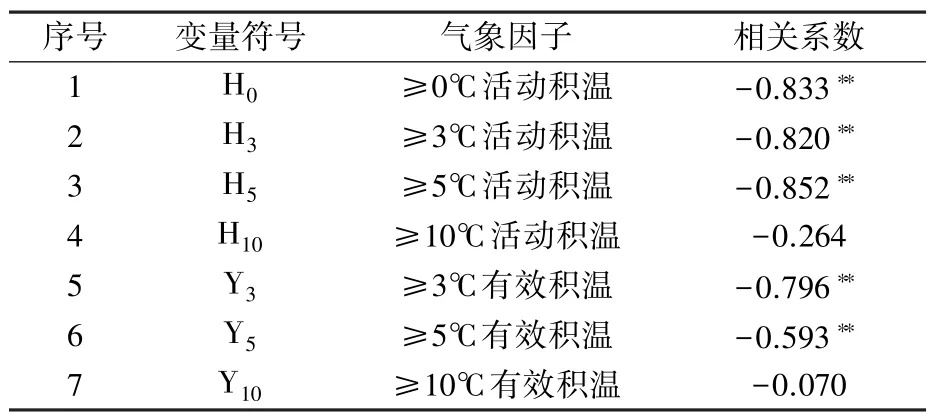
表2 积温因子与盛花期相关系数

2.3 基于多元线性逐步回归建立鸭梨盛花期预测模型

2.3.1 多元线性回归模型的建立 选择2002—2020 年鸭梨盛花期日序数作为因变量，以上文筛选出的13 个与盛花期极显著相关的气象因子作为自变量，利用逐步回归法进行建模。 经过“逐步法”筛选出≥5℃活动积温、≥5℃有效积温、1月平均降水量、1 月上旬平均气温仍然存在严重的共线性，由于≥5℃活动积温与盛花期的相关性极强，所以剔除掉≥5℃有效积温，然后再进行逐步回归，建立了多元线性逐步回归(MLSR)模型，见式(4)。 表3、表4、表5 分别是对模型中各个系数检验和自变量多重共线性诊断结果。 结果表明，自变量VIF 小于10，条件指数在0 ～10 之间，R2＝0.905；模型通过了F 检验，F ＝47.631 ＞F0.010(3，15)＝5.42，P＜0.01，自变量通过了t检验，即模型回归显著，不存在多重共线性。

表3 自变量之间多重共线性诊断结果

表4 模型系数检验结果

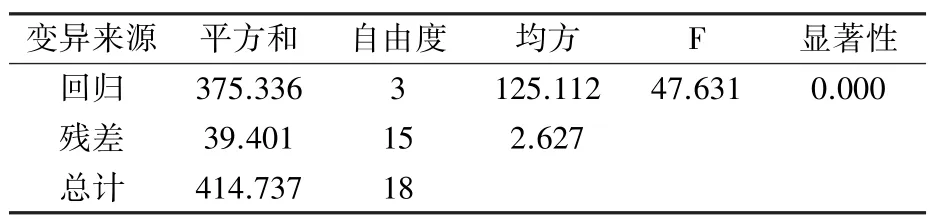
表5 模型方差分析检验结果

式中，Y 是盛花期日序数，H5是1—3 月上旬≥5℃活动积温，T2是1 月上旬平均气温，T16是1 月平均降水量。

2.3.2 模型回代检验 利用建立的多元线性逐步回归模型对2002—2020 年盛花期数据进行拟合，结果(表6)显示，实际盛花期与预测盛花期完全一致年份为2003、2015、2020 年，占15.8%；拟合误差在±1、±2 天的有15 年，占78.9%；拟合误差为±3 的仅有2009 年，占5.3%。

表6 鸭梨盛花期与气象因子模型回代检验

2.4 基于BP 神经网络建立鸭梨盛花期预测模型

首先将筛选出的极显著影响盛花期的13 个气象因子进行归一化处理，作为输入层，输出层为盛花期日序数，然后对气象因子数据集进行网络训练。 采用公式确定隐含层节点数，此处k ＝13，m ＝1，α为[1，10]之间的常数，确定隐含层节点数选取区间为[4，13]。 通过10 次试验结果(表7)可见，当隐含层个数为10 时，训练误差最小，为0.0084，训练结果最佳。

表7 不同隐含层节点数的训练误差

神经元传递函数采用非线性的激活函数tansig，其收敛速度快，可以有效减少迭代次数。 训练算法采用Trainlm 函数，训练次数1 000 次，学习速率设为0.01，训练目标最小误差设为0.001，输出层神经元传递函数采用Purelin 函数。

选择2002—2016 年数据为训练集进行训练，2017—2020 年数据进行测试。 通过计算盛花期预测值与实测值的相关系数，训练集样本两者间的相关系数都在0.860 ～0.972 之间，因此，根据测试集相关系数高低来选择模型，最终选出训练集R2＝0.970、测试集R2＝0.700 的模型为最佳模型，训练集、测试集预测误差均在±2 天以内(图2—5)，未出现误差为±3 天的年份，预测精度较高，较好地模拟出2002—2020 年实际盛花期与预测盛花期的波动变化。

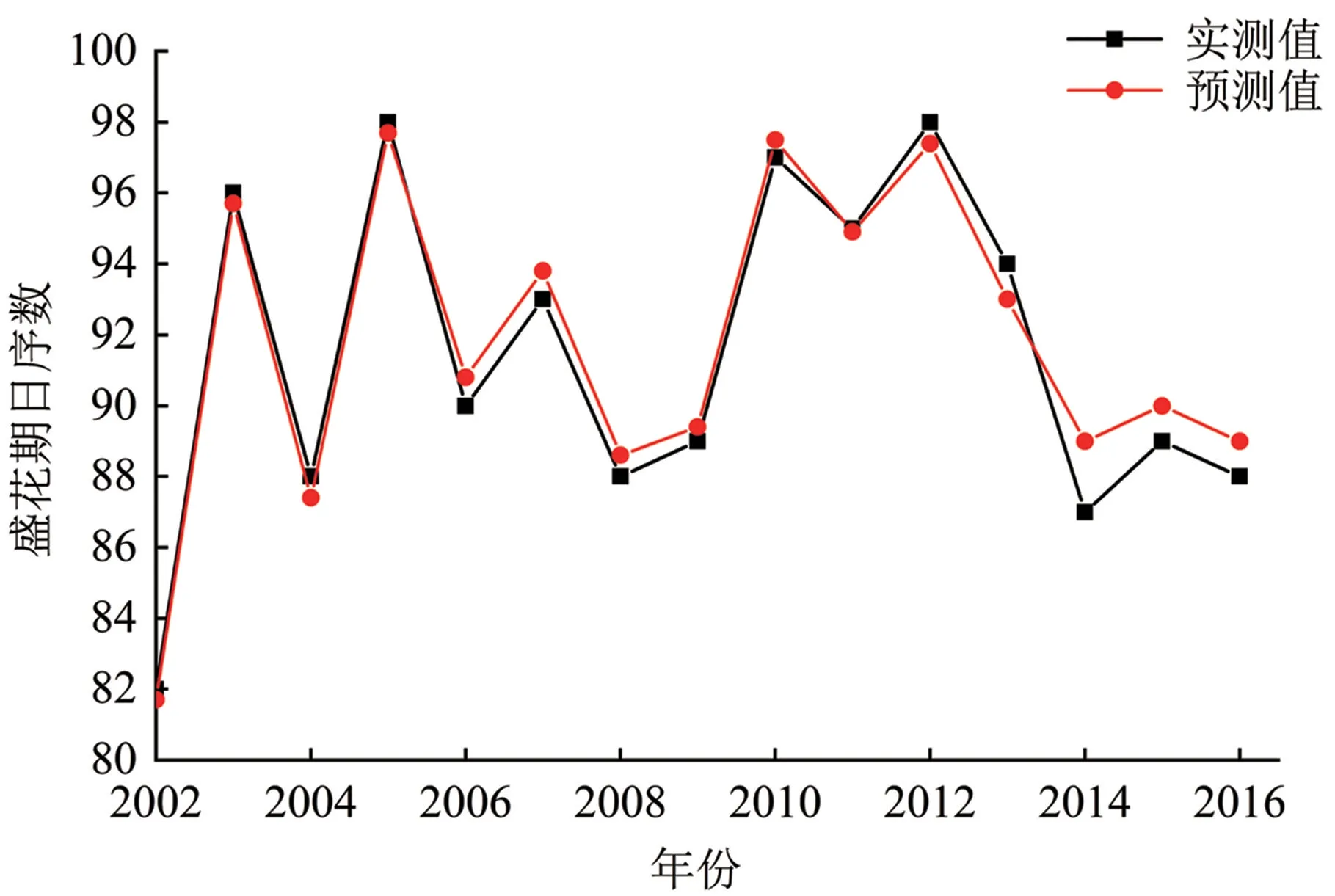
图2 训练样本实测值与预测值

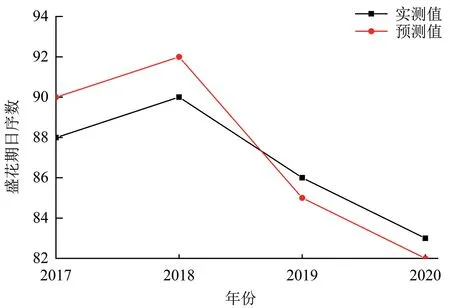
图3 测试样本实测值与预测值

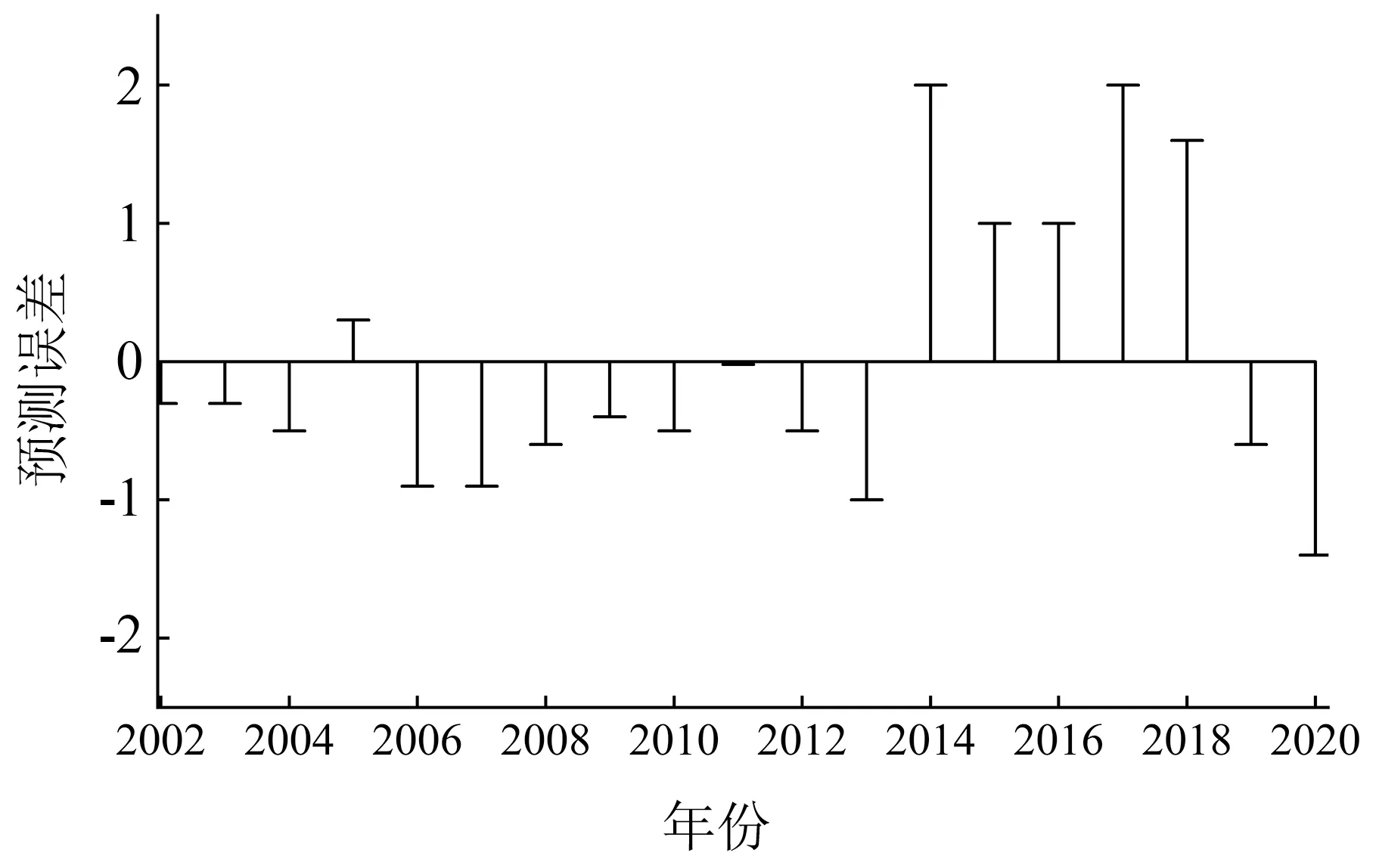
图4 训练集样本误差

2.5 两种模型预测精度的比较评价

通过计算决定系数(R2)、 均方根误差(RMSE)、预测准确率(Rd1)、预测误差率(Rd2)，比较两种鸭梨盛花期预测模型精度，R2越高，RMSE 越小，Rd1越高，预测效果越好。 由表8 可知，BP 神经网络模型的R2为0.950，明显高于多元线性逐步回归模型的R2值(0.905)，说明BP 神经网络模型对盛花期波动趋势拟合度更高；进一步分析两种模型的RMSE、Rd1、Rd2表明，基于多元线性逐步回归的RMSE 为1.45，Rd1为94.7%，Rd2为5.3%。 BP 神经网络RMSE 为1.05，Rd1为100%，Nd2为0。 对比发现，基于BP 神经网络建立的预测模型对鸭梨盛花期的预测精度较高。

表8 两种建立模型预测精度检验

图5 测试集样本误差

2.6 两种建立模型对2021、2022 盛花期的预测效果

利用2021、2022 年的数据对建立的多元线性逐步回归、BP 神经网络模型的预测效果进行验证，结果(表9)显示，多元线性逐步回归模型预测的2021 年盛花期在第84 天，与实际盛花期(2021年3 月23 日)日序数误差为2 天；2022 年盛花期在第86 天，与实际盛花期(2022 年3 月27 日)相符。 BP 神经网络模型预测的2021 年盛花期在第82 天，2022 年盛花期在第86 天，均与实际盛花期观测值相符。 总体来看，两种模型都能很好地预测出2021、2022 年的盛花期时间，且误差较小，尤以BP 神经网络模型的预测准确度更高。

表9 两种建立模型预测效果的验证结果

3 讨论

筛选显著影响花期的气象因子是建立预测模型的基础及提升预测精度的有效方法。 前人研究认为植物花期与其前期气象因素显著相关[19-25]，其中温度是影响花期的重要因素。 因此，本研究通过分析鸭梨盛花期与前期的平均气温、平均最高气温、平均最低气温、活动/有效积温、平均降水量、平均日照时数等气象因子的相关性，筛选出13 个与鸭梨盛花期极显著相关的气象因子作为预报因子，用于预测模型构建。 这13 个因子中，1 月上旬的平均气温、平均最高气温、平均最低气温、1 月平均降水量与鸭梨盛花期负相关的程度最高，可能与当地的气候条件及地理位置有关；1—3 月上旬的≥5℃活动积温与盛花期相关关系最为紧密，这与郭连云[26]、郭睿[23]等的结论相符，即完成某一发育期需要一定数量的积温。

建模方法是影响鸭梨盛花期预测精度的一个重要因素。 在多元线性回归分析中，由于入选的自变量之间容易存在共线性，需要采用“逐步法”剔除冗余信息，以确保自变量之间不存在高度相关性，该算法不仅可以简化计算过程，更能显著提升花期预测模型精度和可靠性[27]；但随着样本数量和自变量的增多，入选的影响花期早晚的因素可能较少，从而导致预测精度不高。 BP 神经网络作为一种按照误差逆向传播算法训练的多次前馈网络，不仅可以储存和学习大量的数据输入和输出，而且不需对变量的映射关系进行表述，具有处理非线性能力；应用反向传播途径不断调整网络的阈值与权值，直到满足误差最小精度条件，输出最优结果[18，28]。 传统的回归模型需要人为选择被预测变量与预测变量之间的模型形式，尤其在数据量较大的情况下，更难选择一个合适且具有代表性的预测模型，所以，在实际应用过程中往往选择简单的多元线性回归模型，但预测精度降低；而BP 神经网络只要建模数据有足够的代表性，利用网络自身的学习能力和速算能力，可以得到一个预测效果比较好的模型。 本试验对魏县鸭梨盛花期的预测结果表明，BP 神经网络预测模型要优于多元线性逐步回归模型。

本研究所建立的模型仅适用于魏县整个区域的鸭梨盛花期预测，而每个梨园的管理水平、地势、地温、树势等条件存在差异，也会影响盛花期，后期有必要针对单个梨园开展更精准的花期预测。

4 结论

魏县地区2002—2020 年的19 年间鸭梨盛花期总体呈现提前趋势，每10 年平均提前2.4 天。1 月平均气温、1 月上旬平均气温、3 月上旬平均气温、1 月上旬平均最高气温、1 月平均最低气温、1 月上旬平均最低气温、3 月上旬平均最低气温、1 月平均降水量及1—3 月上旬的≥0℃、≥3℃、≥5℃活动积温和≥3℃、≥5℃有效积温与鸭梨盛花期极显著负相关，相关系数在-0.575 ～-0.852。逐步多元线性回归、BP 神经网络两种预测模型均可在3 月上旬提前预测盛花期，基于最早盛花期可以提前13 天预报，基于最晚盛花期可以提前29 天预报。 其中，BP 神经网络模型的预测精度更高。