基于邻接表存储与哈希表的频繁项集挖掘算法

吴 昊 刘 钊 顾进广

(武汉科技大学计算机科学与技术学院 湖北 武汉 430065)(武汉科技大学大数据科学与工程研究院 湖北 武汉 430065)(湖北省智能信息处理与实时工业系统重点实验室 湖北 武汉 430065)

0 引 言

频繁项集[1]是从数据资源中挖掘具有潜在价值的信息,频繁项挖掘的经典算法是Apriori算法,但是该算法存在明显的不足:算法的计算时间花费较大和内存空间占用较高。近年来,研究者们根据Apriori算法不足之处提出了改进方法。例如,文献[2]提出了利用数据结构优化预剪枝步骤,结合Spark支持的细粒度计算模型的特征,将事务数据库水平划分为n个块,分配到m个节点,在m个节点上运行IAP算法n次,找到所有频繁项集,利用剪枝的方法有效地减少了频繁项集的挖掘时间,但是每个节点的运行时间由数据块上的节点数决定。文献[3]提出了一种改进的DC-Apriori算法,该算法重构了数据库的存储结构,简化了项集的连接过程,仅需将1个频繁项目集与k-1个频繁项目集结合即可生成k个频繁项目集,从而大大地减少了连接数,只需一次修剪即可直接获取频繁项集,减少了无效的候选项集计算,较好地提高了频繁项集的生成效率。虽然该算法减少了数据的连接次数,但是仍然需要对进数据库进行多次扫描,运算过程比较复杂。文献[4]提出了一种基于MapReduce并行处理的频繁项集挖掘方法,使用Hadoop云计算框架作为数据挖掘平台,引入了矩阵模型并结合MapReduce模型来实现并行化改进Apriori算法,从而缩短算法的运行时间。该算法在处理海量数据集时具有良好的效率和扩展性,但是该算法通常运行在集群中,需要强大的计算和存储能力支撑。曹莹等[5]提出了一种改进Apriori算法,该算法采用事务数据向量矩阵与行候选向量相结合的优化方法,减少生成冗余的候选项集,优化了候选项集计算过程,减少事务数据向量的存储量和项集之间的比较次数,提高频繁项集的挖掘效率。文武等[6]提出了一种结合遗传算法的Apriori算法搜索频繁项集,利用Apriori算法和遗传算法的特点,利用交叉计算产生候选项集和变异算法筛选频繁项集,减少了冗余项集,较好地提高搜索效率。赵学健等[7]提出了一种利用正交链表存储数据所对应的关系矩阵,克服了多次扫描数据库的缺点,同时优化了传统的Apriori算法的自连接和剪枝过程,但是该算法需要利用正交链表存储数据库中的数据,因此对数据的处理量受限于主存空间。

本文提出一种基于邻接表存储与哈希表的频繁项集挖掘算法(ATSAHT-Apriori算法)。该算法利用哈希表的特性,将数据库中的数据进行处理,将数据全部转化为哈希表进行映射,在后续计算项集支持度频数的时候不必进行数据与项集自匹配的过程,由于只需要在哈希表中进行查找来计算项集支持度频数[7],极大地减少了每一轮项集支持度频数的计算时间。由于只需要对数据库中的数据扫描一次存在哈希表中,极大地减少了I/O的时间开销与负载。同时,结合图存储的思想利用邻接表来存储项集,有效地优化了存储项集的内存空间占用,在计算候选项集的过程中,利用堆排序的思想构建大根堆和动态剪枝的思想减少了冗余项集的计算,进一步优化了算法执行时间和内存空间占用。

1 Apriori预测算法简介

Apriori算法是基于一种迭代计算搜索的方式,同时利用频繁k项集的自连接来扩展生成(k+1)项集,首先获取频繁1项集(简称C1),然后通过C1自连接扩展生成候选2项集(简称C2),然后通过候选2项集扩展生成频繁3项集(简称C3),一直迭代下去,直到不能继续扩展生成下一项频繁项集,该迭代方法结束[8]。

由上述步骤可以看出Apriori算法的不足之处:

1) 数据预处理后,每生成一个候选项集时,对数据库每一条数据进行多次扫描,当计算各候选k(k=1,2,…,n)项集的支持度频数,至少要扫描n次数据库中的数据,多次访问数据库将会造成I/O上有较大时间开销与负载,消耗大量的时间[9]。

2) Apriori算法在扩展下一项的过程中扫描数据库中都会因为项集自连接而产生大量冗余的候选项集。例如频繁k项集经过自连接扩展生成所有候选k+1项集Ck+1,就需要进行多次自连接,生成的候选项集与最小支持度比较次数增多,消耗了大量计算时间。项集个数为n的频繁项集Lk,其生成频繁k项集时间复杂度为O(k×n2),在此过程中生成的冗余数据占用了大量的内存空间[10]。

3) 在频繁项集进行扩展生成下一项时,测试C(C∈Ck)里每个(k-1)项集是否是Lk-1中的频繁(k-1)项集,需要扫描[1,k]次Lk-1,对于Lk-1扫描的时间复杂度为O(k×|Lk-1|/2),所以对每一个候选k项集Ck扫描时间复杂度为O(|Ck|×k×|Lk-1|/2),在计算过程中需要消耗大量时间[11]。

根据上述Apriori算法在时间复杂度和空间复杂度的不足,本文提出一种ATSAHT-Apriori算法进行优化。

2 ATSAHT-Apriori挖掘算法

2.1 ATSAHT-Apriori算法描述

邻接表[12](Adjacency List)就是把从同一个顶点出发到达的相邻节点的点和边连接在同一个单链表中,单链表的每个节点代表一条边,称为边节点。每个边节点有三个域:该起点项集对应终点的项集,起点项集与终点项集进行交集后的项集与项集频数,以及指向下一个边节点的指针。在邻接表中,还需要一个用于存储顶点信息的顶点数组。

结合邻接表存储的图节点的思想(关联项集如图1所示,边的权重表示两点项集的支持度频数),邻接表中节点属性(如图2所示),利用邻接表存储频繁项集[13](如图3所示)。

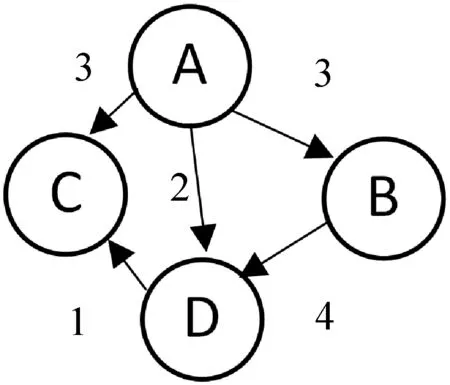
图1 关联项集

图2 链表节点属性

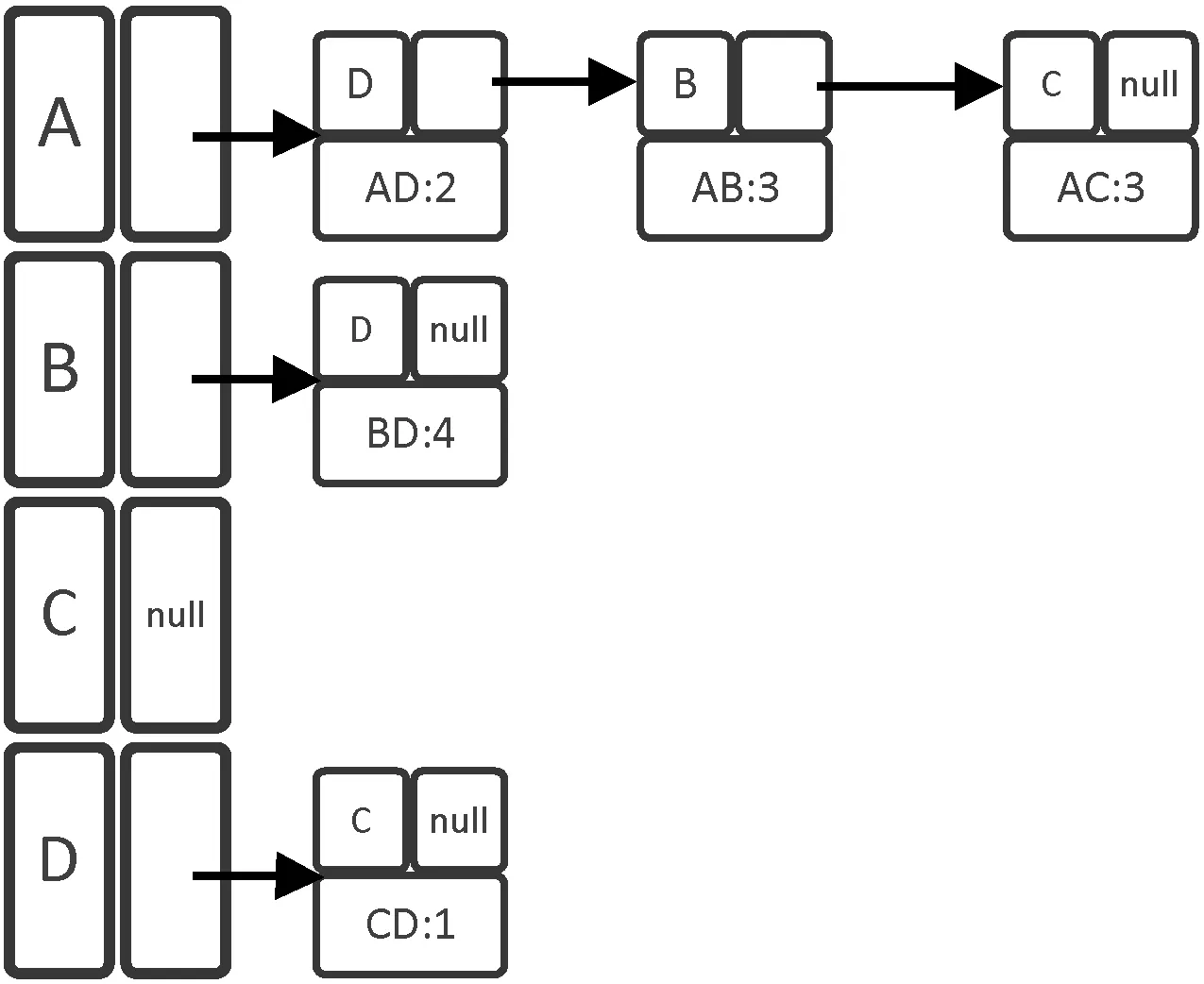
图3 关联项集的邻接表

定义1假定候选项集F=(X1,X2,…,Xn),项集F中的Xi在哈希表Hash=(H1,H2,…,Hn)中的第j(j=1,2,…,n)行中都能通过哈希表找到,证明F中的Xi全部存在于哈希表Hash第j(j=1,2,…,n)行中则候选项集F=(X1,X2,…,Xn)对应的支持度频数计数加1。

定义2如果集合A=(X1,X2,…,Xm)的频数小于最小支持度频数,则A集合是非频繁项集,如果A⊆B,可以判断B=(X1,X2,…,Xm,…,Xn)是非频繁项集[14]。

定义3如果A=(X1,X2,…,Xm,…,Xn)集合的频数大于最小支持度频数,可以判断A是频繁项集,如果B⊆A,则集合B=(X1,X2,…,Xm)所有子集合都是频繁项集[14]。

推论1假设频繁k项集的集合数量记为|Lk|,如果|Lk|

2.2 算法的优化方法

ATSAHT-Apriori算法通过以下方法进行优化:

1) 本文提出一种哈希表存储方式来存储数据,即把数据库中的数据预处理后,存储在哈希表中,然后在哈希表中进行计算项集支持度频数,利用哈希表存储的方法就仅需要扫描一次数据,在后续的过程中极大地减少了I/O的时间开销与负载。

2) 在哈希表中,假设数据有m行,每个候选项集有n个事务,根据定义1,利用哈希表进行计算候选项集支持度频数,在哈希表中进行查找,如果候选项集Q=(X1,X2,…,Xn)中每个项集都能够在该条数据的哈希表的第j(j=0,1,…,n)行中找到,该项集对应的支持度频数计数加1,因此候选项集中的每个事务利用哈希表查找单个项集所需要的时间复杂度为O(1),则查找Q=(X1,X2,…,Xn)项集所需要时间需要O(n),所需要的时间远远小于数据之间进行逐个匹配以及计算项集频繁的时间,优化了计算项集支持度频数的运算过程,极大地优化了计算过程。

3) 将每轮交叉连接生成的项集进行判断,利用哈希表的特性同时结合定义2和定义3,进行动态剪枝,减少了冗余项集的存储和计算过程,优化了计算过程,优化了项集的内存占用空间。

4) 利用哈希表可以判断在当前轮已经计算的项集,将当前轮已经生成的项集及项集支持度频数存入到哈希表中,在后面的计算中,就可以利用哈希表进行判断,如果该项集已经计算过,不需要重复计算,减少了存储冗余项集的计算时间。

5) 利用图存储的思想,利用邻接表存储两点项集生成的候选项集,利用定义2与定义3,结合哈希表对当前轮的项集进行动态剪枝与去除重复项集,将筛选后的候选项集存储在邻接表中,极大地优化了内存空间。

6) 当前轮计算结束后,利用堆排序思想构建大根堆,将候选项集插入大根堆中进行排序,每次删除大根堆中支持度频数最大的项集,并将该项集插入新的邻接表中,当大根堆中最大元素不满足最小支持度后,堆排序结束,剩余的不符合要求的项集不需要排序,将剩余项集存储非频繁项集集合中,为计算下一轮项集优化了存储空间。

3 ATSAHT-Apriori算法的优化

基于前面的定义和推论,算法优化具体步骤如下:

1) 首先扫描数据库,对数据库中的数据进行预处理(假设数据库数据为N条,最小支持度为Min_Sup,由此可以计算出最小支持度频数为Min_sup_Count=N×Min_Sup),按照字母首位进行排序,并且将数据以键-值对映射的方式存储在哈希表Hash_Total中,只需要遍历一次数据库中的数据,就可以将数据存储到哈希表Hash_Total中,在后续的过程中需要在哈希表Hash_Total中进行计算项集支持度频数,因此不需要多次访问数据库中的数据,减少了访问数据库次数,降低了I/O方面的时间开销与负载,然后遍历哈希表计算出每一项的事务频数,得到候选1项集(简称C1)。

2) 对于步骤1)得到的C1,遍历C1中所有项集,对于不满足最小支持度频数的项集直接存入集合res(res存储非频繁项集),事务频数满足最小支持度频数的项集直接存入集合V1(Vi(i=1,2,…)存储频繁项集),此时生成频繁1项集L1(假设L1中数量为n),将L1的2到n项与L1的1到n-1项进行交叉连接取并集可以扩展生成2项集。

3) 根据推论1,如果|Lk|≥k+1,可以继续扩展下一项,此时利用L1[i]和L1[j]的项集交叉连接进行取并集生成新的项集flag,首先判断flag是否在哈希表Hash_Item出现,如果该项集存在哈希表Hash_Item中,则不需要进行计算该项集频数,直接进行该轮下一个项集计算,反之,进行下一步计算:如果flag是集合Vi(Vi存储频繁i(i=1,2,…,k)项集)项集中的子集,根据定义3进行动态剪枝,则不需计算该项集频数,同时将项集flag中对应的支持度频数设置为Min_sup_Count,并进行该轮下一个项集计算,反之,继续下一步计算,如果flag是res中项集(res集合存储非频繁项集)的子集,根据定义2利用哈希表进行动态剪枝,则不需要进行计算该项集支持度频数,直接进行当前轮下一个项集计算,反之,继续进行下一步,遍历该项集中每一个事务,在哈希表Hash_Total中进行查找,时间复杂度为O(1),根据定义1可知,如果该轮项集在哈希表Hash_Total中第i行(i=1,2,…,n)都找到的话,该项集的支持度频数计数加1,遍历哈希表Hash_Total中的每一行,重复定义1的步骤,就可以计算该项集对应的支持度频数,计算该项集支持度频数结束后,利用哈希表Hash_Item(key表示该项集,value对应项集频数)键-值对存储此次计算的项集与项集频数,每一次计算项集支持度频数结束后,就将项集插入到邻接表中,此轮遍历结束就可以生成候选2项集邻接表,将一维列表ansk(k=2)遍历邻接表,并存储邻接表中的每一个节点,然后利用堆排序的思想对ansk进行部分堆排序[13],构建大根堆(递减排序出项集频数满足最小支持度的项集,其余的项集为非频繁项集不需要进行排序,将频繁项集存储在Vi(i=2)中,非频繁项集存储在res中,就计算得到了频繁2项集L2。

4) 通过推论1判断,如果|Lk|≥k+1,说明利用Lk中的频繁项集可以计算(k+1)项,重复步骤2)和步骤3)中求下一项频繁项集的过程,并且通过频繁k项集来继续扩展第k+1项的频繁项集。

5) 重复循环步骤4),利用推论1,直到第k项频繁项集的数量小于k+1,就表明无法进行下一层寻找更多的频繁项集,查找频繁项集算法结束。

ATSAHT-Apriori算法核心的伪代码描述如下:

ATSAHT-Apriori (){

将Database每条数据中的事务映射存入哈希表Hash_Total中(N表示有N行哈希表);

/*定义存储候选集列表ansk(k=1,2,…)表示第k项集,ansk[i](i=1,2,…,M)表示k项集中的矩阵的第i个事务(ansk[i].count表示k项集的第i个事务的支持度频数,初始化为0),Vk(k=1,2,…)存储第k项频繁项集,res存储所有非频繁项集。*/

FOR(i=0;i

WHILE遍历哈希表Hash_Total[i].items():

ans1[Hash_Total[i].key].count++;

//对事务进行计数

END FOR

FOR(i=0;i

IF(ans1[i].count>=Min_sup_Count)

V1.append({ans1[i].key:ans1[i].count});

//将频繁项集存入V1

ELSE

res.append({ans1[i].key:ans1[i].count});

//将非频繁项集存入res中

END FOR

FOR(k=2;|Vk-1|.length()>=k+1;k++)

M=dict();

//定义新的哈希表

FOR(i=1;i<|Vk-1|.length()-1;i++) DO

p=Vk-1[i].key;

//表示k-1项集中第i行事务

FOR(j=i+1;j<|Vk-1|.length();j++) DO

q=Vk-1[j].key;

//表示k-1项集中第j列事务

/*p∪q表示交叉连接取的项集赋值给flag */

flag=p∪q;

IF 哈希表Hash_Item出现过flag

/*不用重复计算,计算下一个项集*/

Continue;

IF flag是Vk中的子集

/*根据定义4判断,直接设置为最小支持度,计算下一个项集*/

M[flag]=Min_sup_Count;

Continue;

IF flag是res中的子集

/*根据定义3判断,继续计算下一项集*/

Continue;

FOR(p=0;p

/*计算项集频数*/

//遍历哈希表Hash_Total,N表示哈希表行数

FOR(h=0;h

//遍历项集flag中的每一项事务。

IF Hash_Total[p][flag[0-->flag.length()-1]]存在

//根据定义2,计算每个候选项集频数

//flag所有事务在第p行哈希表中能找到

M[flag]++;

/*项集计数*/

END FOR

END FOR

/*哈希表Hash_Item(Hash_Item的key表示项集,value对应项集频数)对来存储项集与频数。*/

Hash_Item[flag]=M[flag];

将(q=Vk-1[j].key,M[flag])插入p=Vk-1[i].key的邻接表中,链表尾端设置为NULL;

END FOR

END FOR

遍历当前轮的邻接表,将每一个项集及对应的频数存储在一维列表ansk中;

fre_item,unfre_item=ATSAHTApriori_Sort(ansk);

/*对项集频数构建大根堆排序。筛选出符合最小支持度的前k个项集,不符合条件的项集不用排序*/

Vk.insert({fre_item.key:fre_item.count});

res.insert({unfre_item.key:unfre_item.count});

END FOR}

ATSAHT-Apriori_Sort(ansk){

/*以频繁项集的数量为标准,用堆排序思想构造大根堆进行排序*/

调用堆排序算法进行部分排序[13]

//fre_item为频繁项集,unfre_item为非频繁项集

fre_item,unfre_item=heap_Sort(ansk);}

4 ATSAHT-Apriori算法的优化验证

假设最小支持度为0.4,经过数据预处理之后有效数据数量有10条(如表1所列),就可以计算出最小支持度频数为4,即min_support_count为4。

表1 数据库数据

1) 首先对数据进行预处理,然后将数据库中有效数据存储到哈希表Hash_Total中(见表2)。

表2 数据对应的哈希表

2) 计算哈希表Hash_Total中每个事务对应的支持度频数,计算之后可以得到候选1项集以及支持度频数(见表3),将该项集支持度频数构建大根堆,并且利用堆排序的思想对部分项集频数进行递减排序(对于项集对应的支持度频数如果相同,则按照名称的首字符递增排序,只需要将符合最小支持度的项集进行排序),筛选之后就得到频繁1项集L1=[[A4],[A5],[A2],[A7],[A8],[A9],[A1]],如表4所示。对上述计算出来的频繁1项集(L1),可以计算出频繁1项集对应长度|L1|=7≥k+1,同时利用L1构建候选2项集邻接表用来存储候选2项集,根据推论1可以得出,可以利用L1继续扩展候选2项集(候选2项集邻接表如图4所示),把L1的项集进行交叉连接取并集,就可以扩展生成出有效的候选2项集,然后利用哈希表Hash_Total就可以计算出项集对应的支持度频数,然后生成链表节点插入到对应的邻接表中。

表3 候选1项集表

表4 频繁1项集表

图4 候选2项集邻接表

3) 从频繁k(k≥2)项集开始,利用k-1频繁项集交叉连接取并集的过程中,可能会出现重复的频繁项集需要计算。

(1) 如果该项集在之前的计算过程中存在,则不用重复计算项集支持度频数,继续计算当前轮下一个项集。

(2) 如果符合定义3,项集的子集经过判断后不是频繁项集,则利用哈希表进行动态剪枝操作,不必计算该项集的支持度频数,继续计算当前轮下一个项集。

(3) 根据定义4,如果该项集超集是频繁项集,不用计算该项集频数,直接设置该项集支持度频数为min_support_count,继续计算当前轮下一个项集。

(4) 这样极大地减少冗余项集的无效计算,如果计算生成的候选项集(没有执行前几个过程,称为候选项集),对该候选项集中每一个事务和哈希表Hash_Total中的第p(p=1,2,…,N)行的数据进行检索,如果项集中每一个事务都能在哈希表第p(p=1,2,…,N)行中找到,根据定义2,则每在一行找到就在项集支持度频数计数加1),每次计算完项集支持度频数后,将项集与项集支持度频数存储在链表节点中,将链表节点插入到邻接表中。

4) 通过遍历候选2项集的邻接表,可以得到候选2项集以及对应的支持度频数,根据堆排序的思想,利用项集支持度频数建立大根堆,并且利用堆排序的思想对部分项集频数进行递减排序(只需要对于项集支持度频数满足最小支持度的项集排序),经过堆排序筛选之后就得到频繁2项集,L2=[[A4,A5],[A5,A7],[A2,A4],[A2,A5],[A4,A7],[A4,A8],[A4,A9],[A5,A8],[A5,A9],[A1,A5],[A2,A8],[A2,A9]]。

5) 因为|L2|=12≥k+1(k=2),根据推论1,因此可继续扩展生成频繁3项集集合。利用频繁2项集L2构建候选3项集邻接表,可以利用L2继续扩展生成候选3项集,fi表示频繁2项集(fi=[[A4,A5],[A5,A7],[A2,A4],[A2,A5],[A4,A7],[A4,A8],[A4,A9],[A5,A8],[A5,A9],[A1,A5],[A2,A8],[A2,A9]])。将L2的项集进行交叉连接取并集,就可以扩展生成出候选3项集(如图5所示),重复进行步骤3)-步骤5)的过程就可以计算下一项频繁项集。

图5 候选3项集邻接表

6) 按照步骤5)中求频繁项集的方法,就可以扩展得到频繁3项集,|L3|=4≥k+1(k=3),L3=[[A2,A4,A5],[A4,A5,A7],[A4,A5,A8],[A4,A5,A9]],满足推论1条件,继续向(k+1)项扩展,进而求出(k+1)频繁项集。

7) 重复步骤6)中计算(k+1)项的处理,如果无法满足推论1的条件,表示无法计算出下一项频繁项集,算法结束,输出所有的频繁项集。

5 算法的效率分析

5.1 算法时间复杂度分析

Apriori算法求频繁项集所需要的时间是由数据量的大小M、每条数据的事务项长度L所决定的,项集个数为|Ck|,每一次扫描数据库数据并计算项集支持度频数时间复杂度是O(M×L×|Ck|),扫描数据库后就要开始进行项集的自连接平均的时间复杂度为O(|Ck-1|×|Ck-1|),在这个过程中,经过动态剪枝的时间复杂度为O(|Ck|),判断符合最小支持度的平均时间复杂度为O(M×|Ck|),所以Apriori算法计算频繁项集所需要总时间为[16]:

T1=O(M×L×|Ck|)+O(|Ck-1|×|Ck-1|)+

O(|Ck|)+O(M×|Ck|)

本文利用哈希表的方式存储数据库的数据,并且用哈希表查找的方法来计算项集支持度频数,利用邻接表存储每次计算的候选项集。利用哈希表只需要扫描一次数据库,将数据库数据映射到哈希表中进行存储,避免了多次扫描数据库而消耗时间,因此主要在项集交叉连接以及在哈希表中计算频繁项集的过程中消耗的时间。假设数据库的数量为M,即哈希表的行数为M,哈希表查找的时间复杂度为O(1),每一轮产生的候选项集为Ck,频繁项集为L=Lk,冗余项集剪枝与去重的项集减少的时间为T,构建大根堆进行排序的时间复杂度O(CklogLk),则近似推算出所需要的总时间大约为:

O(CklogLk)

5.2 算法的空间复杂度分析

Apriori算法求频繁项集计算所需要的内存空间是频繁项集和非频繁项集的数量所决定,该算法项集在内存空间上消耗近似为[16]:

S1=O(|Ck|×|Ck|)+O(|Lk|)

本文利用哈希表检索来计算频繁项集支持度频数,并且用邻接表来存储候选项集,每次存储的候选项集为Ck,该算法中项集所占用在空间上面的消耗近似为:

S2=O(|Ck|)+O(|Lk|)

对比两种算法的时间复杂度和空间复杂度可以看出:T2

6 实验验证分析

本文针对传统Apriori算法与文献[7]中的算法(简称OLL-Apriori算法)和ATSAHT-Apriori算法在相同环境下进行对比实验,数据集为毒蘑菇的相似特征,来自于UCI数据集:数据集包含了8 124条样本和23个特征,将数据顺序随机排列进行分组然后对比实验。

第一组实验设置最小支持度为0.1,在数据数量逐渐递增的情况下进行比较两种算法的时间效率。实验对比如图6所示。

图6 不同数据运行时间对比

通过图6中的实验对比,说明当最小支持度一定时,随着数据量的增多而增多,所花费的时间也会逐渐增多。在相同的环境下,ATSAHT-Apriori算法在时间效率上明显提高,花费的时间明显小于其他两个算法。

第二组实验采用最小支持度为0.01,在相同环境进行实验,在数据数量递增的情况下进行比较三种算法的内存空间占用,实验结果如图7所示。

图7 不同数据占用内存空间对比

通过实验对比可知,随着数据量范围的不断增加,产生的数据分支也会随之增多,产生的频繁项集也会慢慢增加,作为对比的三种算法内存空间占有率都会增加,但是相比之下,经过优化后的ATSAHT-Apriori算法的时间效率与内存空间占用明显优于其他两种算法。综合以上实验结果表明,在相同环境下,经过优化后ATSAHT-Apriori算法时间效率得到了明显的提高,内存空间占有得到明显的减少,说明了ATSAHT-Apriori方法达到了预期的效果。

7 结 语

本文利用哈希表的特性,提出利用哈希表来存储数据库中的数据,并且利用哈希表来计算项集的支持度频数;利用动态剪枝算法与哈希表去除重复项集减少了大量的冗余项集,并结合图存储的思想,利用邻接表存储项集交叉连接生成的候选项集;利用堆排序算法对候选项集进行部分排序生成频繁项集,极大地优化了频繁项集的计算速度与内存空间。本文算法对Apriori算法的时间复杂度和空间复杂度的不足之处进行了较大的优化,通过实验数据对比分析,验证了改进后的算法在运行时间和内存开销有明显优化的效果。但是当数据量较大时,项集交叉连接和计算频繁项集时同样存在非常大的计算量,在今后的研究中将会结合Hadoop框架,实现并行化计算处理,以期得到更好的效果。