三种“有初速度的双棒”问题的归类例析
2023-08-10刘万强肖梦军
刘万强 肖梦军
(湖北省松滋市第一中学)
有初速度的两导体棒在电磁感应问题中,因安培力随电流的变化而变化,运动情况较复杂,涉及电路、动力学、动量和能量多维度的知识综合分析,能力要求高,试题的区分度好,成为命题者青睐的选题素材。本文把“有初速度的双棒”问题分成三种情况,分别以电路、动力学、动量和能量四个角度进行归类例析如下。
一、宽度恒定的导轨,一棒有初速度、一棒没有初速度
【问题情境】如图1所示,光滑平行金属导轨,两根完全相同的金属棒ab、cd(质量m、电阻R、长度l)导轨电阻不计。整个装置处在竖直向下的强度为B的匀强磁场中,t=0时给ab一个向右的速度v0,试分析两杆的运动、动量和能量变化过程(假设导轨足够长,两杆始终不相撞)。
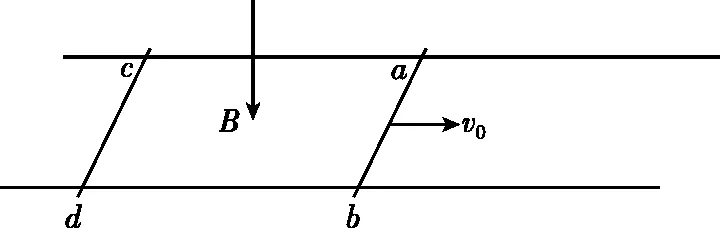
图1
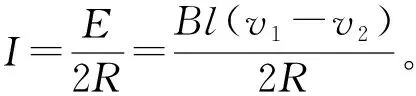
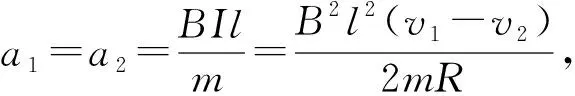
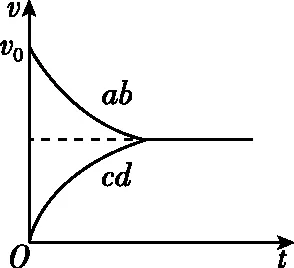
图2
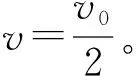
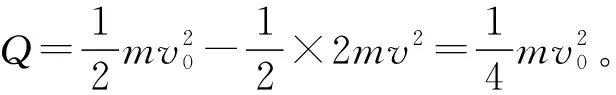
【典例1】两根足够长的固定的平行金属导轨位于同一水平面内,两导轨间的距离为L。导轨上放置两根导体棒a和b,俯视图如图3所示。两根导体棒的质量均为m,电阻均为R,回路中其余部分的电阻不计,在整个导轨平面内,有磁感应强度大小为B的竖直向上的匀强磁场。导体棒与导轨始终垂直接触良好且均可沿导轨无摩擦地滑行,开始时,两棒均静止,间距为x0,现给导体棒a一水平向右的初速度v0,并开始计时,可得到如图4所示的Δv-t图像(Δv表示两棒的相对速度,即Δv=va-vb。
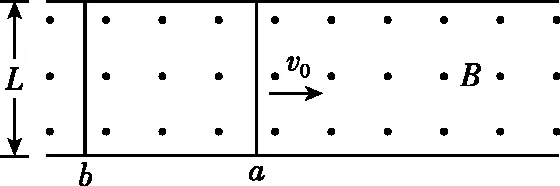
图3
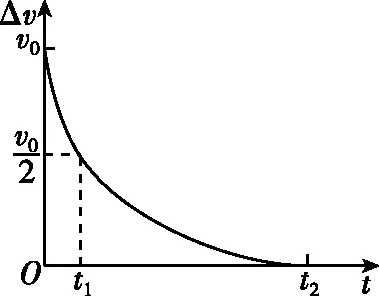
图4
(1)试证明:在0~t2时间内,回路产生的焦耳热Q与磁感应强度B无关。
(2)求t1时刻棒b的加速度大小。
(3)求t2时刻两棒之间的距离。
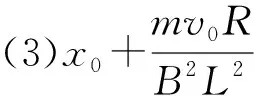
【解析】(1)t2时刻开始,两棒速度相等,由动量守恒定律有2mv=mv0
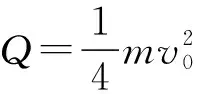
所以在0~t2时间内,回路产生的焦耳热Q与磁感应强度B无关。
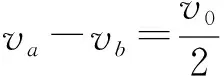
此时棒b所受的安培力F=BIL
由牛顿第二定律得棒b的加速度大小
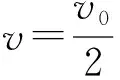
0~t2时间内,对棒b,由动量守恒有
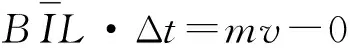
而ΔΦ=BΔS=BL(x-x0)
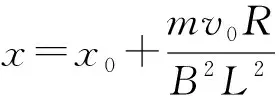
二、宽度恒定的导轨,两棒有相反初速度
【问题情境】如图5所示,光滑平行金属导轨,两根完全相同的金属棒ab、cd(质量m、电阻R、长度l)导轨电阻不计。整个装置处在竖直向下的强度为B的匀强磁场中,t=0时分别给ab、cd一个向右、向左的速度v1和v2,且v1>v2,试分析两杆的运动、动量和能量变化过程(假设导轨足够长,两杆始终不相撞)。
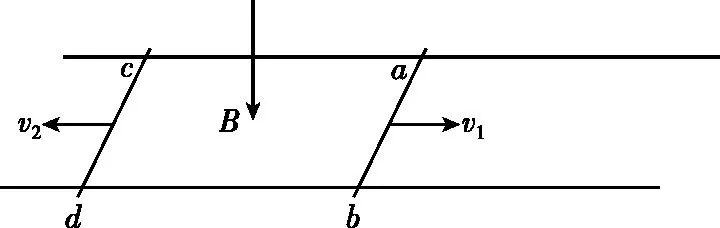
图5
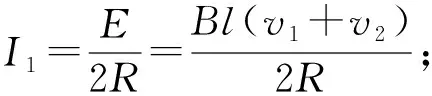
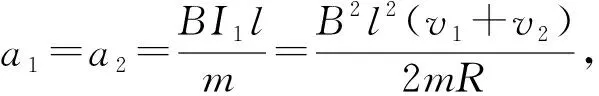
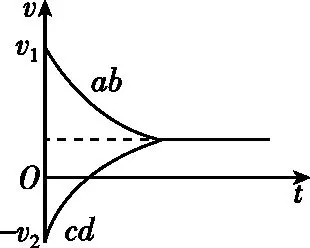
图6
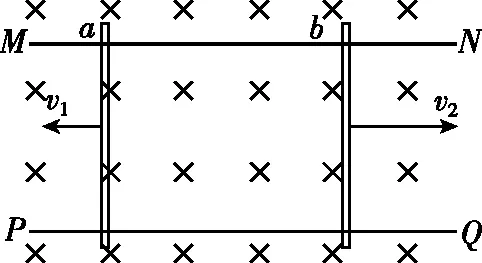
图7
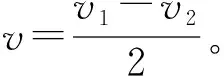
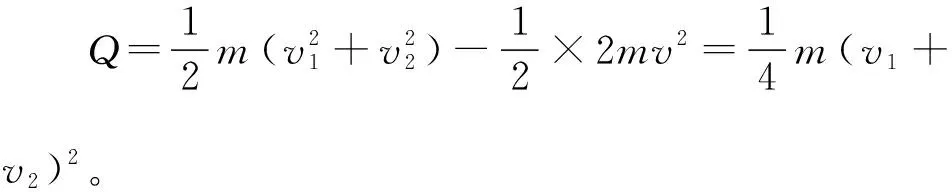
【典例2】如图所示,在水平面上有两条足够长的平行导电导轨MN、PQ,导轨间距离L=1.0 m,匀强磁场垂直于导轨所在的平面(纸面)向里,磁感应强度的大小为B=1.0 T,两根导体棒a、b放置在导轨上,并与导轨垂直,它们的质量均为m=1 kg,电阻均为R=0.5 Ω,两导体棒与导轨接触良好,与导轨间的动摩擦因数均为μ=0.2。t=0时,分别给两导体棒平行导轨向左和向右的速度,已知导体棒a的速度v1=2 m/s,导体棒b的速度v2=4 m/s,重力加速度g=10 m/s2,导轨电阻可忽略,最大静摩擦力略大于滑动摩擦力。
(1)求t=0时刻,导体棒a的加速度;
(2)求当导体棒a向左运动的速度为零时,导体棒b的速率;
(3)已知导体棒a向左运动的速度为零后,b向右运动s=0.35 m速度变为零,求该过程经历的时间t和导体棒b产生的焦耳热。
【答案】(1)8 m/s2,方向水平向右 (2)2 m/s
(3)0.825 s,0.65 J
【解析】(1)t=0时刻,两导体棒和导轨构成回路,回路中的总电动势为
E=BL(v1+v2)=6 V
根据闭合电路欧姆定律可知回路中的电流为
对导体棒a,根据牛顿第二定律可得
BIL+μmg=ma
解得a=8 m/s2
t=0时刻,导体棒a的加速度大小为8 m/s2,方向水平向右。
(2)在导体棒a、b运动时,两导体棒受到的摩擦力大小相等,方向相反,根据左手定则可知两导体棒受到的安培力也等大反向,两导体棒组成的系统合力为零,满足动量守恒,以向右为正方向,当导体棒a向左运动的速度为零时,根据动量守恒可得mv2-mv1=mv3
解得导体棒b的速率为v3=2 m/s
(3)导体棒b的速率为v3=2 m/s时,回路的感应电动势为E′=BLv3=2 V
导体棒a受到的安培力为
由题意最大静摩擦力略大于滑动摩擦力,则有
fmax>μmg=2 N
可知导体棒a的速度为零后,不再运动,从导体棒a的速度为零至导体棒b的速度为零的过程,导体棒b受到的安培力冲量为
对导体棒b根据动量定理可得
解得t=0.825 s
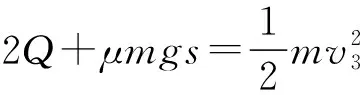
解得Q=0.65 J
三、宽度不同的导轨,一棒有初速度、一棒没有初速度
【问题情境】如图8所示,光滑平行金属导轨,左端导轨宽度为l,右端导轨宽度是左端宽度的一半,两根完全相同的金属棒ab、cd(质量m、电阻R、长度l)导轨电阻不计。整个装置处在竖直向下的强度为B的匀强磁场中,t=0时给ab一个向右的速度v0,试分析两杆的运动、动量和能量变化过程(假设导轨足够长,两杆始终不相撞,且始终在导轨上)。
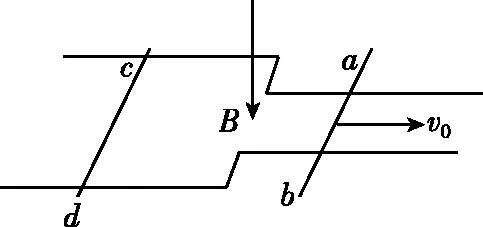
图8
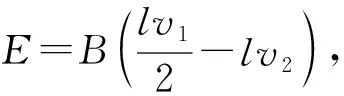
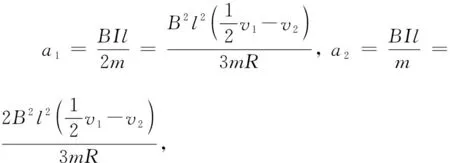
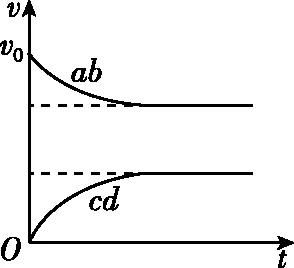
图9
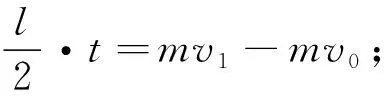
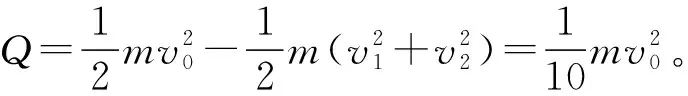
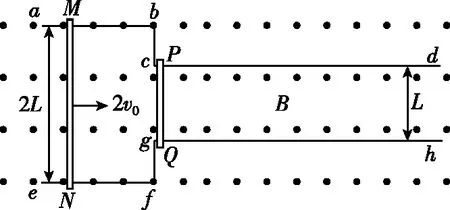
图10
(1)MN棒运动到导轨ab、ef的最右端时,MN棒的速度大小;
(2)回路中电流再次为零时,PQ棒最终产生的总热量。
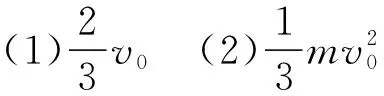
【解析】(1)MN棒从开始至运动到导轨ab、ef的最右端时,对于MN,根据动量定理有
-BI·2l·t=2mv1-2m·2v0
对于PQ,根据动量定理有BI·l·t=mv2-0
由于MN棒运动到导轨ab、ef的最右端时,回路中电流恰好为零,此时有v2=2v1
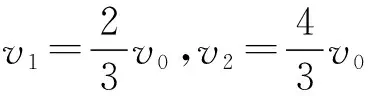
(2)当MN棒运动到导轨ab、ef的最右端时,系统产生的总热量为
在这个过程中PQ棒产生的热量为
当MN棒运动到cd、gh导轨上至电流再次为零时,MN、PQ棒的速度相等,根据动量守恒定律有mv1+mv2=2mv
此过程系统产生的热量为
在这个过程中PQ棒产生的热量为
PQ棒最终产生的总热量为Q总=Q1+Q2
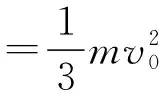
四、总结

