基于运输成本最小化对水果公司市场选址的研究

吕浩东 张国华

摘 要：文章先使用Qgis软件将果农位置坐标化，并且将果农售水果量的不同转化为运输批次的不同，进而引入权重，利用权重重心法求解水果市场的坐标；同时，客户区到市场的距离和运输批次也会影响水果市场的选址，所以要将这两方面比较分析找出最适合水果公司的市场选址方案。利用Excel软件进行权重化处理，对区域坐标求解，并进一步分析得出水果运输公司成本最小化的市场坐标。

关键词：水果市场；市场选址；权重重心法

中图分类号：F252.2文献标志码：ADOI：10.13714/j.cnki.1002-3100.2023.12.019

Abstract： The paper first uses Qgis software to coordinate the location of fruit farmers， and converts the different sales of fruits by fruit farmers into different transportation batches. Then， weights are introduced， and the weight center of gravity method is used to solve the coordinates of the fruit market. Meanwhile， the distance from the customer area to the market and the transportation batch will also affect the location of the fruit market. Therefore， it is necessary to compare and analyze these two aspects to find the most suitable market location plan for the fruit company. The weighting process is carried out by Excel software， the regional coordinates are solved， and the market coordinates of the fruit transportation company are further analyzed to minimize the cost.

Key words： fruit market; market location; weight center of gravity method

0    引    言

水果园林的主要功能是生产水果，当前很多地区已把水果产业纳入主导产业中[1]，本文研究的内容就是针对山东省部分村落水果经济的发展助力水果市场选址。关于选址模型，本文针对市场提出了协同效应定义和三种不同的协同效应函数，其中协同效应的最大俘获选址模型是考虑市场规模对消费者选择行为产生影响的竞争设施选址研究[2]。除了市场规模因素以外，自然环境、社会政策、消费群体和竞争环境等也是影响市场选址的重要因素[3]；本研究从这几方面分析并且评估其重要程度，利用多因素分析选址，再对研究个体进行聚类是多因素选址的完整逻辑。在实际生活中，ATM选址问题就符合这一逻辑，提出和设计一种基于Voronoi图和修改的K中心点聚类的求解算法[4]，并结合实际问题进行运算。另一方面，在分析、总结区域市场零售业连锁经营发展特点的基础上建立连锁网点选址布局的市场吸引力模型，运用元胞自动机模拟技术进行区域市场连锁网点选址与布局的仿真研究。利用仿真技术模拟问题，将实际问题抽象化，是研究问题的有效处理方式[5]。同时，选址问题除要正向考虑外界条件以外还应该从本身特点出发，以物流中心所覆盖的（服务目标） 需求量为约束条件建立选址模型并完成选址[6]，在物流中心选址模型的思路方面完成逻辑上的、完全逆向的思维方式转变。在分析了选址因素以后，还需要对选址模型进行一定介绍。在选址模型中，遗传算法与重心法属于经典且常用的模型。根据节约遗传算法对电子商务配送路径实施优化，以便获取全局最优路径[7]，并通过解析物流配送中心模式使其更符合实际需求。建立电子商务配送中心的选址模型，利用目标函数运算出变动成本与时间约束条件，对选址模型进行改进[8]对于缩短配送所需时间与成本具有重要意义。在前置仓选址中利用重心法解决生鲜产品的选址问题，也为市场选址提供了一定的借鉴价值。

1    基于运输成本最小化权重重心选址方法

1.1    选址流程与选址步骤

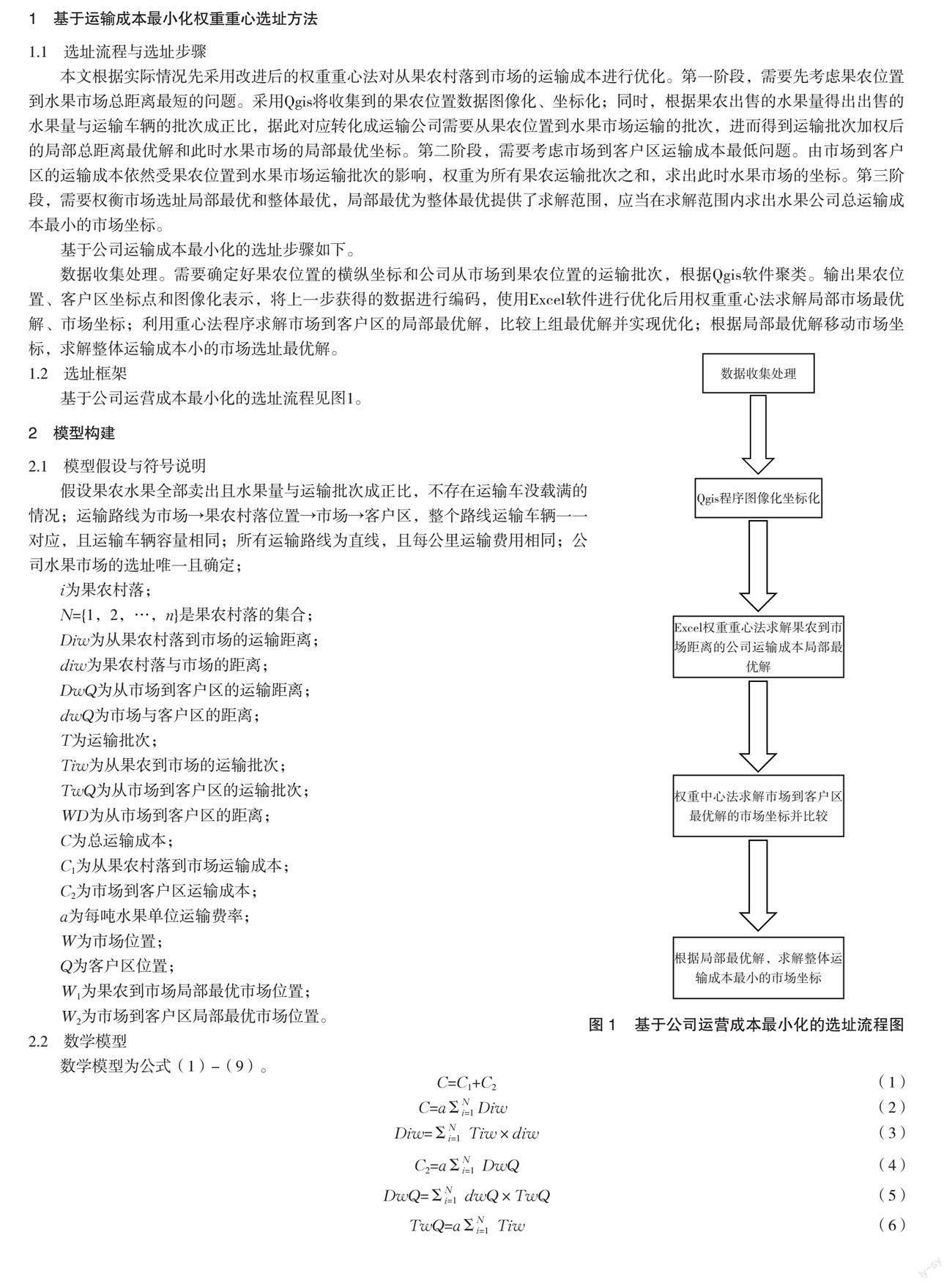
本文根据实际情况先采用改進后的权重重心法对从果农村落到市场的运输成本进行优化。第一阶段，需要先考虑果农位置到水果市场总距离最短的问题。采用Qgis将收集到的果农位置数据图像化、坐标化；同时，根据果农出售的水果量得出出售的水果量与运输车辆的批次成正比，据此对应转化成运输公司需要从果农位置到水果市场运输的批次，进而得到运输批次加权后的局部总距离最优解和此时水果市场的局部最优坐标。第二阶段，需要考虑市场到客户区运输成本最低问题。由市场到客户区的运输成本依然受果农位置到水果市场运输批次的影响，权重为所有果农运输批次之和，求出此时水果市场的坐标。第三阶段，需要权衡市场选址局部最优和整体最优，局部最优为整体最优提供了求解范围，应当在求解范围内求出水果公司总运输成本最小的市场坐标。

基于公司运输成本最小化的选址步骤如下。

数据收集处理。需要确定好果农位置的横纵坐标和公司从市场到果农位置的运输批次，根据Qgis软件聚类。输出果农位置、客户区坐标点和图像化表示，将上一步获得的数据进行编码，使用Excel软件进行优化后用权重重心法求解局部市场最优解、市场坐标；利用重心法程序求解市场到客户区的局部最优解，比较上组最优解并实现优化；根据局部最优解移动市场坐标，求解整体运输成本小的市场选址最优解。

1.2    选址框架

基于公司运营成本最小化的选址流程见图1。

2    模型构建

2.1    模型假设与符号说明

假设果农水果全部卖出且水果量与运输批次成正比，不存在运输车没载满的情况；运输路线为市场→果农村落位置→市场→客户区，整个路线运输车辆一一对应，且运输车辆容量相同；所有运输路线为直线，且每公里运输费用相同；公司水果市场的选址唯一且确定；

i为果农村落；

N={1，2，…，n}是果农村落的集合；

Diw为从果农村落到市场的运输距离；

diw为果农村落与市场的距离；

DwQ为从市场到客户区的运输距离；

dwQ为市场与客户区的距离；

T为运输批次；

Tiw为从果农到市场的运输批次；

TwQ为从市场到客户区的运输批次；

WD为从市场到客户区的距离；

C为总运输成本；

C1为从果农村落到市场运输成本；

C2为市场到客户区运输成本；

a为每吨水果单位运输费率；

W为市场位置；

Q为客户区位置；

W1为果农到市场局部最优市场位置；

W2为市场到客户区局部最优市场位置。

2.2    数学模型

数学模型为公式（1）-（9）。

2.3    模型求解

模型的求解步骤如下。

确定客户区的编码、经纬度和各个果农村落点的编码、经纬度、水果出售量、水果运输批次；利用Qgis软件对客户区和所有果农村落的X、Y坐标进行图像化处理，并求解关于运输批次的权重；利用Excel软件通过规划求解方式确定果农村落到市场的局部最优解；根据重心法程序求解市场到客户区的最优解；利用Qgis将两个局部最优解的坐标图像化表示，并确定整体最优解的范围；把在局部最优解两点之间求整体最优解的方式转化为所有位置加权后最短距离的求解；利用Excel求解整体运输成本最小的市场坐标。

2.4    算例求解

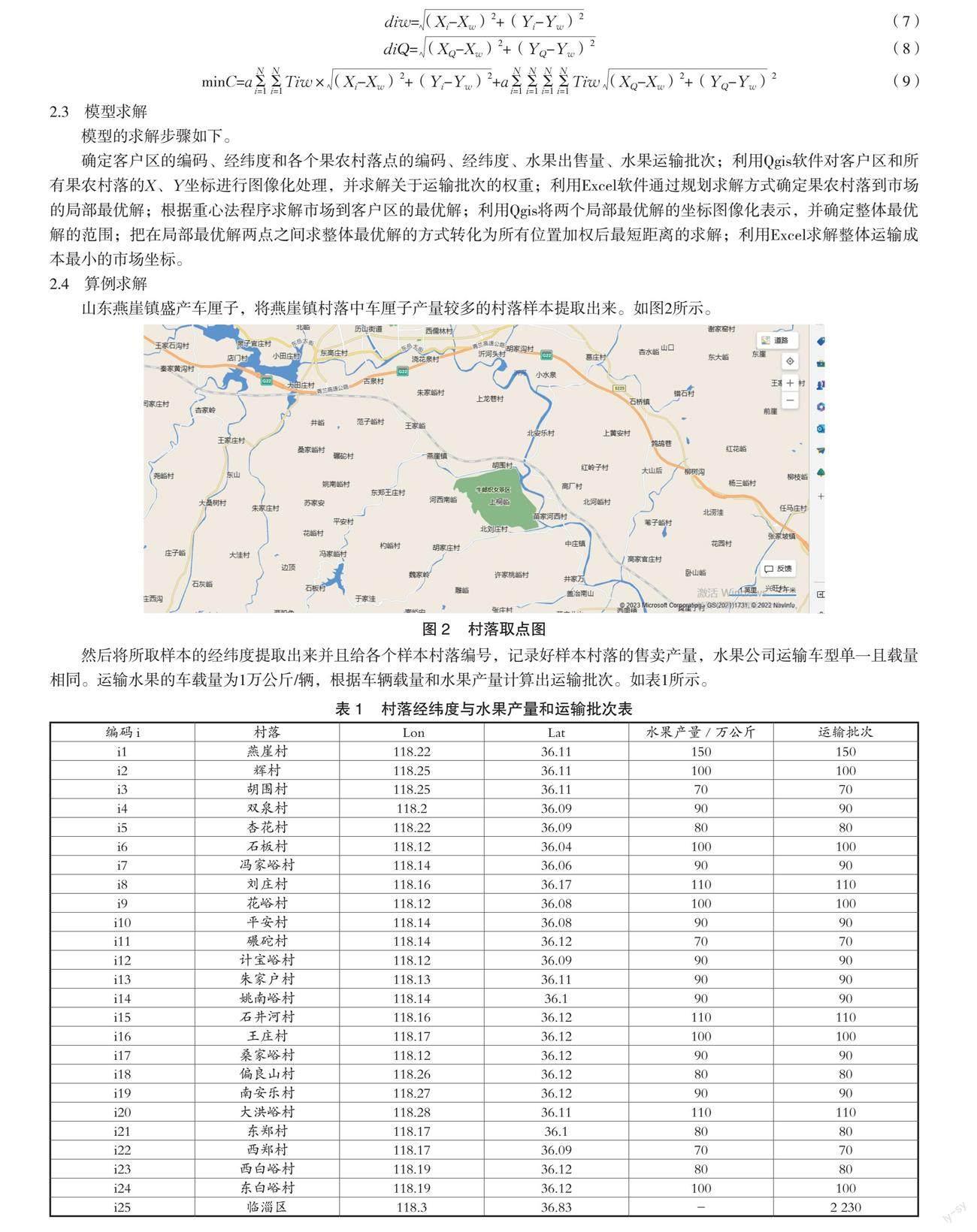
山东燕崖镇盛产车厘子，将燕崖镇村落中车厘子产量较多的村落样本提取出来。如图2所示。

然后将所取样本的经纬度提取出来并且给各个样本村落编号，记录好样本村落的售卖产量，水果公司运输车型单一且载量相同。运输水果的车载量为1万公斤/辆，根据车辆载量和水果产量计算出运输批次。如表1所示。

记录好客户区的经纬度并对其进行编码，汇总村落样本跟客户区并用Excel记录，利用Qgis软件把果农村落位置跟客户区位置导入Qgis，用图表展现出来，如图3所示。

3    果农村落到市场的局部最优解

首先进行Excel编码，把经纬度与X、Y坐标的关系进行转换，就可以利用村落之间的经纬度计算点与点之间的距离，编码单位为米，平均运输费率为每公里10元，在计算总成本的时候应该乘以0.001来配平公里与米之间的单位转换；同时将运输批次作为权重，也要注意从市场到果农村落再从果农村落到市场这个距离是运输批次的两倍，最后计算运输成本时应该注意运输批次的2倍变化导致距离增加为原来的2倍，因此运输成本变为原来的2倍。如表2所示。

然后将总运输成本求和，利用Excel中的规划求解，目标为总运输成本最小；需要改变的点为市场的坐标，利用非线性求解求得市场坐标和总运输成本。如表3所示。

当市场经纬度为（118.175 4，36.106 42）时，果农村落与市场间的运输费用为215 644.912 2元、市场与客户区的运输费用为1 811 334.052元、总费用为2 026 978.964 2元，此时达到局部最优。如表4所示。

4    市场到客户区的局部最优解

当市场到客户区的运输费用最低时，市场应直接建立在客户区。此时市场与客户区的经纬度坐标一致，利用Excel计算数据如表5所示。

此时，市场经纬度为（118.3，36.83），总运输费用为3 633 282.719元，达到局部最优。很明显此时的局部最优解的运输成本远大于第一种方式，所以整体最优解应该位于两个局部最优解市场坐标连线中，更靠近第一个局部最优解的位置。

5    整体最优解

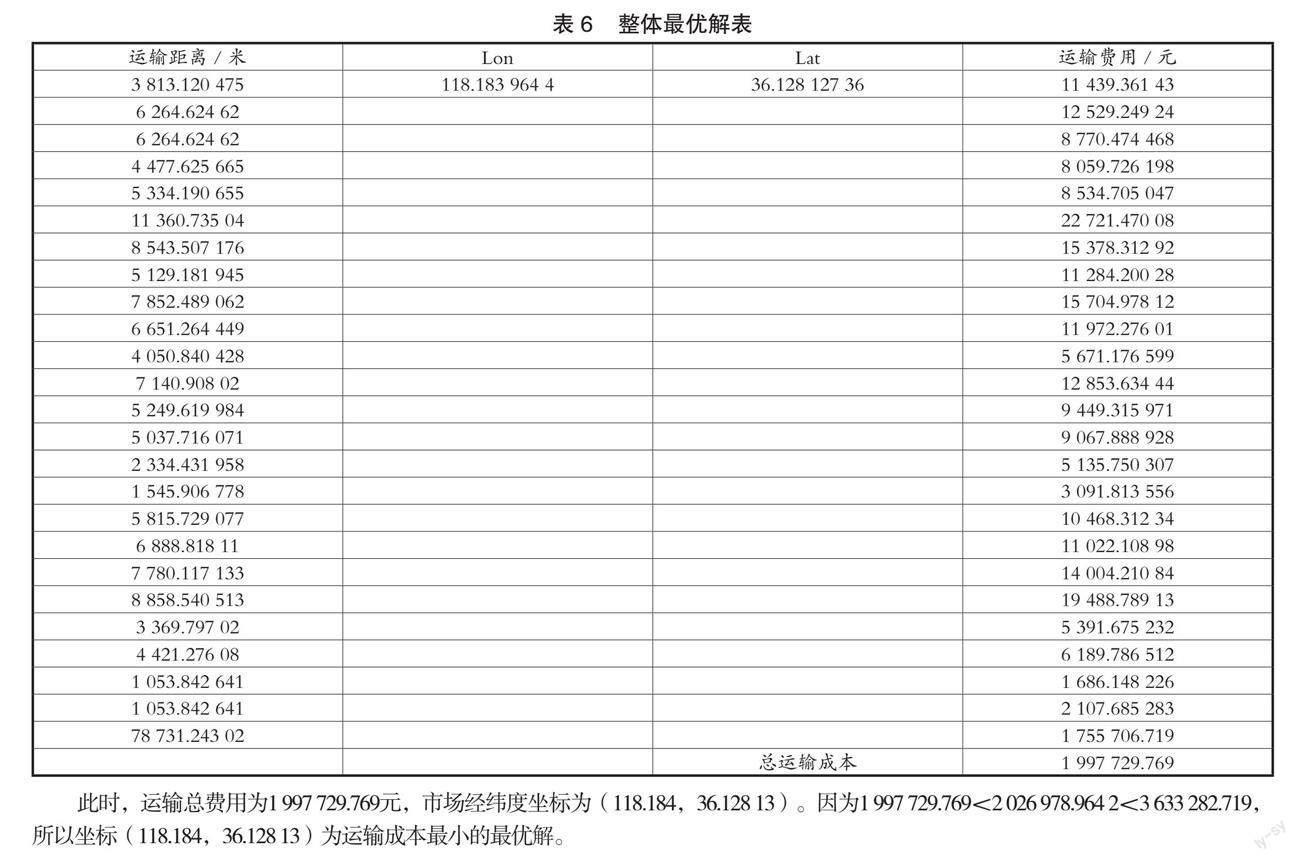
整体最优解的范围应位于两个局部最优解之间；当我们切换思路，整体问题就变成了果农村落+1，权重叠加的最小运输费用的问题。计算结果如表6所示。

此时，运输总费用为1 997 729.769元，市场经纬度坐标为（118.184，36.128 13）。因为1 997 729.769＜2 026 978.964 2＜3 633 282.719，所以坐标（118.184，36.128 13）为运输成本最小的最优解。

6    结    语

本文通过运输费用的变化研究市场选址，利用运输批次和距离的改变引起运输费用的变化，从而影响市场的选址。在研究思路上，先从局部最优入手确定市场选址的范围，再从整体角度出发，利用运输费用最低的选址本质，将客户区看作运输批次上权重叠加的“果农村落”，构建了基于果农村落n+1的运输费用最低模型，在思路研究上实现了创新。然而，本文在运输车辆的选择上只考虑了单一车型，且运输车辆恰好能装满村落的水果量、果农村落与市场间的距离是以直线计算，这些与实际生活存在的偏差是本文研究中的不足之处。

参考文献：

[1] 李永先，贺永仙，王庆，等．广安市水果园林下经济产业发展现状及建议[J]．现代农业科技，2020（11）：104-106.

[2] 朱华桂，乔联宝．有市场协同作用的竞争设施选址：模型与比较[J]．系统工程理论与实践，2013，33（11）：2831-2838.

[3] 任金政，杜浦，陈宝峰．影响村镇集贸市场选址决策的因素研究[J]．安徽农业科学，2010，38（22）：12236-12238.

[4] 周继恩，冯兴，冯鑫．一种基于市场真实情况的ATM选址模型的研究及应用[[J]．计算机应用与软件，2018，35（2）：117-120.

[5] 田志友，王浣尘，吴瑞明．区域市场连锁经营选址与布局的元胞自动机模拟[J]．系统工程理论方法应用，2005（1）：50-54.

[6] 李五四，李砚．以市场需求为逻辑起点的物流中心选址模型构建[J]．统计与决策，2007（17）：166-167.

[7] 唐棣华，卫欣．基于節约遗传算法的电子商务配送中心选址[J]．计算机仿真，2022，39（5）：158-162.

[8] 赵振强，张立涛，王文钊，等．基于顾客需求量分布的生鲜农产品前置仓选址研究[J]．计算机应用与软件，2021，

38（10）：107-113，124.