掌握物理核心概念“压强”突破“固体切割叠加”问题

杨莉 常超 牟银勇

摘  要：以初中物理阶段的典型试题为素材，对以考查压强知识为载体的“固体切割叠加”情境类试题进行分类，按照不同类型总结归纳“切割”“叠加”和“切割叠加组合”三种典型情境的解题思路，并以重庆市2020年、2021年和2022年近三年中考试卷中相关的真题为例，梳理解题思路，展示固体切割叠加问题的解析过程。

关键词：压强；固体切割叠加；重庆市；中考试题

中图分类号：G633.7 文献标识码：A    文章编号：1003-6148（2023）7-0040-6

1    問题来源

课标对压强部分的内容要求是通过实验，理解压强；知道增大和减小压强的方法，并了解其在生产生活中的应用［１］。课标对“压强表示压力作用效果”“压强指单位面积上受到的压力大小”等概念内容的要求是“理解”层次，可见压强内容在初中物理阶段中的重要性。重庆近年中考题都涉及到以固体的切割和叠加为情境的压强考查，考查的题型主要有选择题、填空题和计算题，且都集中在各类题型的最后一题处，分值在2分至6分不等，可见切割叠加模型的分析在中考中的重要地位。切割叠加模型往往组合考查，受力面积和压力大小都会发生变化，以“压力”“重力”“压强”“高度”等各种物理概念呈现题干，结合图像和数值计算或比值运算，要求学生读懂情境丰富的题目，掌握准确的物理概念，进行精准快速的运算，考查学生的综合能力，难度较大。故以典型试题为素材，对切割叠加类问题进行分类，归纳总结解决固体切割叠加类问题的思路方法，再以重庆市2020年、2021年和2022年三年中考试卷中相关的真题为例，展示固体切割叠加问题的解析过程。

2    结合压强的切割叠加问题的基本类型

这类试题常以固体压强为考点，按照固体切割类型、重叠类型、切割重叠组合类型可分成三大类，各自继续细分，呈现常见的情境和对应的试题描述，如表1所示。

3    结合压强的切割叠加问题的解题思路

分析引起压强变化的原因，需充分理解压强的核心概念。根据压强的定义可知，无外乎是改变其压力大小和受力面积大小两种类型导致，所以分析的重心始终是各类情境下压力和受力面积的比值如何变化［２］。合理利用题干中的已知情境，例如初始状态两个物体的压强相等，高度和面积可通过图像直接看出，则应直接使用压强定义的变形式F=pS分析出两个物体的压力关系，进而分析出二者的重力和质量关系；同时把握柱形固体的特点，用p=F/S公式可导出柱形固体的压强还可以用p=ρgh进行求解，从而分析出二者的密度关系。反之，若是初始状态已知二者的压力关系，则用逆向思维将上述公式进行变形反推即可。具体分类总结如表1所示。

3.1    固体切割类型引起的压强变化

（1）判断：对于固体的切割类型，首先判断是竖向切割还是横向切割。

（2）竖向切割：无论是二者切去相同质量或相同体积还是相同厚度，压力和受力面积均会随之发生改变，但压力和受力面积的比值相同。无论使用定义式F=pS或柱形固体适用的导出式p=ρgh，均可分析出竖向切割不影响物体对地面的压强值（未全部切完的情况下）。

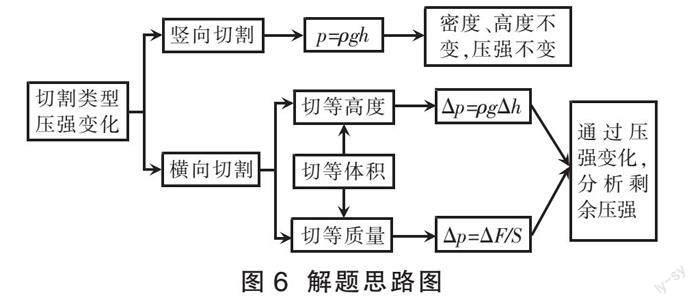
（3）横向切割：横向切割题目情境需要具体分类，在比较剩余部分对地面的压强时，往往会陷入矛盾境地，例如图1中甲、乙两物体最初对地面压力相同，则可知ρ<ρ，切去相同高度时，对于剩余部分甲的高度虽大但密度小，利用常规思路p=ρgh分析发现无法比较二者剩余部分对地面的压强大小。故在横向切割情境下，对于切去相同高度往往使用公式Δp=ρgΔh分析出变化量，再用p'=p-Δp即原压强减去压强变化量比较两个剩余部分对地面的压强；对于切去相同质量等效于压力变化量相同，则往往使用公式Δp=ΔF/S分析出变化量，再用p'=p-Δp比较剩余部分对地面的压强；而对于切去相同体积则需要结合到两个物体的面积关系，将体积关系转化为高度关系或者压力关系，再按上述“切高度”或者“切质量”的思路继续求解。综上，切割类型引起压强变化的具体解题思路如图6所示。

3.2    固体叠加类型引起的压强变化

（1）判断：当两个底面积不同的物体重叠在一起后，新的整体就不再是上下底面积一样的柱形固体了，故推导式p=ρgh就不再适用。因此，对于叠加类型求解压强只能用压强的定义式p=F/S进行求解。对于固体叠加类问题，首先判断是上小下大还是上大下小类型，不同的类型对应的压力和受力面积不同。

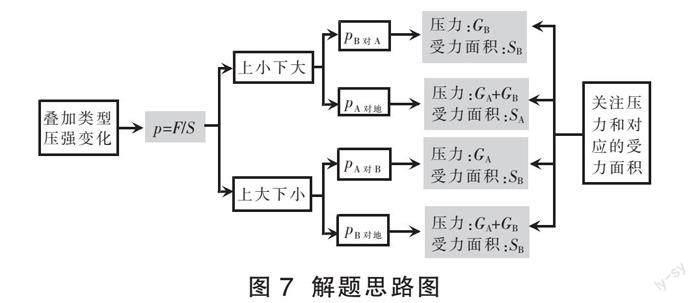
（2）对照：充分理解压强定义中涉及到的压力和受力面积两个核心概念，对平衡物体进行平衡状态下的受力分析很关键。对于上方物体，支持力与重力二力平衡，故它对下方物体的压力大小等于自身重力；下方物体静止时受到自身重力、上方物体施加的压力（数值上等于上方物体的重力）、地面施加的支持力，故它对地面的压力就等于两个物体的重力之和，受力面积是指压力真正作用的面积。以图2和图3的情境为例，固体叠加类型的具体解题思路如图7所示，其关键在于找准所求物理量对应的压力值及其对应的受力面积。

3.3    固体切割叠加组合类型引起压强变化

（1）判断：对于切割叠加模型，首先判断是一方被切割，然后将切下部分直接叠至对方的单向叠加类型；还是双方都被切割，然后将各自切下部分互相叠放于对方的剩余部分的双向叠加类型。

（2）单向叠加：单向叠加情境下，对于单方被切的物体，根据题目横切还是竖切，回到上述基本的切割类型解题思路；对于单向被叠加的物体，回到上述基本的叠加类型解题思路。

（3）双向叠加：对于两个物体都被切割，同时将切割下来的部分叠加至对方剩余部分上，情境是最复杂的。如果是竖直切割，则被切割的物体压力和受力面积都会发生变化，但由于是等比例变化，故一般设未知数表示被切下的比例，则压力和面积都可以用同一个未知数进行表达，更便于计算；如果是横向切割，则受力面积不发生改变，只有压力发生改变，此时设切去部分的压力或者比例为未知数都可以。固体切割叠加组合类型的具体解题思路如图8所示，对于该类型，其题目呈现形式无论是图像还是比值，其解题技巧几乎都是方程思想。

4    重庆中考固体切割叠加类试题解析

按照上述解题思路，以重庆市近三年来的中考真题中切割叠加类问题为例，展示固体切割叠加问题的具体解题思路和解析过程。

例1 （2022年A卷第8题） A，B两个质量均匀的正方体放在水平地面上，如图9甲所示，B的边长是A的2倍，将A沿竖直方向切去宽为L的部分，把切去部分叠放在B上，B对地面的压强pB与L的变化关系如图9乙所示。切割后，A剩余部分对地的压强为pA，则以下分析正确的是（   ）

A. B的重力是50 N

B. L=2.5 cm时，pA：pB=16：21

C. B的底面积为100 cm2

D. A切去一半后，pA=2 000 Pa

解题思路 该模型属于上述的切割叠加组合类型中的单向切割，A被切割，B被叠加。具体来说A是被竖直切割，则其剩余部分对地面的压强始终不发生变化；B被叠加后对地面的压力变成两部分重力之和，受力面积不发生改变。结合图像两个特殊点，起始点是A未被切割状态，终止点是A全部被切割，通过特殊点分析二者的其他物理量。

解析 由图可知，lA=10 cm，lB=2lA=20 cm，SA=l=100 cm2，SB=l=400 cm2，故GB=pBSB=5×103 Pa×4×10-2 m2=200 N，GA=△F=△pBSB=1×103 Pa×4×10-2 m2=40 N，则p'A=pA=FA/SA=GA/SA=4 000 Pa；当A被切去2.5 cm时，根据长度比值知切去部分占A的1/4，故p'B=（GA+GB）/SB=（10 N+200 N）/4×10-2 m2=5 250 Pa，p'A：p'B=16：21。

答案：B。

例2 （2022年B卷第8题） 有A，B两个均匀实心圆柱体，A的高为5 cm、底面积为20 cm2，B的高为8 cm、底面积为50 cm2。若将它们按图10甲、乙的方式放在水平桌面上，A对桌面的压强为p1=1×103 Pa，B对桌面的压强为p2；若按图丙的方式放置时，B对A的压强为p3=6×103 Pa，A对桌面的压强变为p4。下列判断正确的是（    ）

A. A的重力是20 N

B. B的密度为3.0 g/cm3

C. p3：p2=2：5

D. p4=1.6×104 Pa

解题思路 该模型属于上述叠加类型中的上大下小情境。p1和p2是二者单独放置时的对地压强，求解方法是用各自的重力大小除以底面积即可；上大下小重叠后，B对A的压强p3和A对地的压强p4的受力面积相同，都应取SA，二者壓力大小不同，前者压力大小等于B的重力大小，后者压力大小等于A，B的重力大小之和。

解析 单独放置时GA=FA=p1SA=1×103 Pa×2×10-3 m2=2 N，GB=FB=p3SA=6×103 Pa×2×10-3 m2=12 N，同时VB=SBhB=400 cm3，故ρB=GB /gVB=1 200 g/400 cm3=3 g/cm3；因为p2=FB/SB=GB/SB=2 400 Pa，故p3：p2=

5：2；p4=F'/SA=（GA+GB）/SA=（2 N+12 N）/2×10-3 m2=7 000 Pa。

答案：B。

例3 （2021年A卷第13题） 如图11所示，ABC是以O为支点的轻质杠杆，AB=40 cm，OB=30 cm，OC=60 cm，水平地面上的实心均匀正方体物块M重为80 N，用细线与C点相连，在A点用60 N的力沿某方向拉杠杆，使M对地面的压力最小，且杠杆处于水平位置平衡，此时细线的拉力为               N；保持A点的拉力大小和方向以及杠杆的状态不变，要使M对地面的压强变为原来的8/15，可将物块M沿竖直方向切去的质量为               kg（忽略支点处的摩擦）。

解题思路 此题考查内容是杠杆结合压强，综合切割类型的情境，比较新颖。首先结合杠杆知识，动力大小和阻力臂不变情况下，动力臂最长时，阻力最大，此时M对地面的压力最小，根据此时的压力和物体底面积求出此时对地的压强值。第二问为竖切类型，但有所不同的是拉力保持不变的情况下，压力和受力面积不再成比例变化，故该模型属于切割和重叠组合的模型，只是“叠加”的是一个恒定向上的拉力而不是向下的压力。但重力和受力面积依旧是比例变化，故可根据比值建立方程思想。

解析 由勾股定理得，OA=50 cm，由杠杆平衡条件F1l1=F2l2得知，60 N×50 cm=F×60 cm，解得F=50 N。对物体进行受力分析，得出地面对物体的支持力F=G-F=30 N。设切去后剩余部分占物体的n倍，n为分数，同时由于底面积未知，设物体底面积为S，则根据前后压强关系p'=8p/15，建立方程：=×，约掉方程两边的S，代入重力和拉力的数值，解出n=25/32，则切去部分占比为7/32，乘以总质量8 kg，得出切去1.75 kg的质量。

答案：50；1.75。

例4 （2021年B卷第8题）如图12所示，质量分布均匀的甲、乙两个正方体叠放在水平地面上，甲放在乙的中央。若乙的边长是甲的2倍，甲对乙的压强与乙对地面的压强相等。将它们分别放入足够多的水中静止时上下表面都处于水平位置，正方体乙漂浮且有3/10的体积浸入水中，下列判断正确的是（）

解题思路 此题是浮力结合压强，综合上小下大的重叠类型的情境，比较新颖。首先根据边长关系可找出二者面积和体积关系，同时结合重叠模型的两个压强，可以逆推出两个物体间的重力关系。当重力和体积已知后，可求出密度和两个物体置于水中的浮沉情况，从而对浮力进行求解。

例5 （2020年B卷第12题） 甲、乙为两个质量分布均匀的实心圆柱体，放置在水平桌面上，沿水平方向切去上部分，剩余部分对桌面的压强p与切去部分高度h的关系如图13所示，已知甲的密度为4.0×103 kg/m3，则圆柱体甲的高度为

cm。当切去的高度为12 cm，将各自切去部分放置在另一个圆柱体的剩余部分的上表面时，甲剩余部分和乙切去部分的组合体对桌面的压强为p1，乙剩余部分和甲切去部分的组合体对桌面的压强为p2，且p1：p2=3：2，则甲、乙圆柱体的底面积之比为                 。

解题思路  首先判断该题型是以压强为考点，以切割重叠中的双向叠加为情境，由于题干的呈现方式是图像，将题目的难度再次拔高。先找到图像中的特殊点，当甲、乙未被切割时，各自自然放置对地面的压强已知，结合乙最终被切完的总高度已知，甲的密度已知，可利用柱形固体压强推导式p=ρgh，分析出甲的总高度和乙的密度值。当切去的高度已知并交换叠加后，只能用总压力除以总面积的思路建立方程，其中切去的高度会改变各自的重力，可以用切去部分比值表示，减少方程的计算量。

5    结束语

当掌握好压强的核心概念后，就能基于概念视角准确找到特定压强对应的“压力”“受力面积”，同时需要根据题意判断属于哪类的切割叠加问题，并充分理解上述的基本解题思路，以压强为核心考点、以切割叠加为情境的题型便能迎刃而解。在创新题型中，切割叠加类型可以结合到浮力或者杠杆等相关力学知识求解，情境多变，更要求学生能够掌握力学概念的核心要义，配合严密的受力分析，方能抓住内核以不变应万变。这也要求教师在日常教学中，重视物理最基础的概念教学和对学生分析能力的培养，引导学生从各类题型中抽象出关键模型，发展科学思维和物理核心素养；同时教师也需要多提炼和反思总结，方能授学生以“渔”，更好地实现师生关系的教学相长。

參考文献：

［１］中华人民共和国教育部．义务教育物理课程标准（２０２２年版）［Ｓ］．北京：北京师范大学出版社，２０２２．

［２］人民教育出版社，课程教材研究所，物理课程教材研究开发中心．义务教育教科书物理八年级下册教师教学用书［Ｍ］．北京：人民教育出版社，２０１６．

（栏目编辑    陈  洁）