基于改进PSO的有源噪声控制算法关键参数在线获取

李春阳, 金光灿, 刘 浩

(1.上海工程技术大学机械与汽车工程学院, 上海 201600;2.上海理想汽车科技有限公司, 上海 201800)

0 引言(Introduction)

自20世纪80年代滤波-x最小均方(FxLMS)算法被提出以来,对于ANC算法的研究蓬勃发展[1-2]。为了获得更好的降噪能力,新提出的有源控制算法引入了各种调节参数,这些关键参数对于算法降噪性能具有显著的影响,不合适的参数会使ANC系统的降噪能力显著下降,甚至失效。在过去的研究中,一般采用试错法获取合适的参数值,试错法通过反复比较使用不同参数时算法的降噪效果,从中选取最优的参数,但是该方法费时低效[3]。MENG等[4]将PSO优化引入变步长ANC算法,用于优化该算法的步长调节因子。JIANG等[5]将改进PSO算法用于混合ANC (HANC)系统关键参数的获取,并取得了降噪效果的提升。MENG和JIANG的方法是使用相同的输入信号进行粒子群寻优,实质仍然是离线获取最优参数值,其方法并不能直接在实时ANC系统中使用。

为了解决ANC参数难以设置的问题,本文提出了一种能用于在线更新ANC关键参数的改进PSO算法。该算法在ANC系统采样噪声信号的同时,实时优化更新参数值。仿真结果表明,提出的改进PSO算法能很好地与常见的ANC降噪算法相结合,实现在线获取关键参数的最优值,保证ANC系统优秀的降噪效果。

1 有源噪声控制系统(Active noise control system)

有源噪声控制系统是利用声波相消干涉的原理,通过产生幅值相同、相位相反的次级声波抵消不期望的噪声[6]。常见的单通道前馈控制结构如图1所示。其中,主路径为参考传感器到误差传感器之间的声音传播路径,次级路径指次级声源到误差传感器之间的路径。该系统的工作过程如下:噪声源产生噪声并通过主路径传递;参考传感器拾取参考信号x(n)作为控制滤波器的输入信号,控制滤波器对信号x(n)进行滤波并输出相应的控制信号y(n),y(n)驱动次级声源产生抵消声波,初级噪声和次级抵消声波在误差传感器处叠加相消形成局部静音区,误差传感器拾取抵消后的残余误差信号e(n),x(n)和e(n)共同作用于自适应算法的更新,算法根据相应的控制准则不断在线调整滤波器权系数。整个过程持续不断,最终ANC系统会获得稳定的降噪效果。

图1 单通道前馈有源噪声控制示意图Fig.1 Schematic diagram of single channel feedforward active noise control

2 改进的粒子群算法及其在ANC中的应用(Modified PSO algorithm and its application in ANC)

2.1 标准粒子群优化算法

粒子群算法是受鸟群觅食规律启发而衍生出的一种进化算法,该算法的核心思想是利用个体共享的信息,促使整个群体的运动在求解空间中从无序到有序逐渐演化,最终获取问题的最优解[7]。假设种群有N个粒子,并在D维的搜索空间进行搜寻,则第i个粒子当前位置为Xid=(xi1,xi2,…,xiD),速度为Vid=(vi1,vi2,…,viD),目前搜索到的个体最优位置为Pid,pbest=(pi1,pi2,…,piD),群体最优位置为Pd,gbest=(p1,gbest,p2,gbest,…,pD,gbest),PSO算法根据公式(1)和公式(2)迭代更新粒子的速度和位置:

(1)

(2)

其中,i为粒子序号,i=1,2,…,N;d为粒子维度序号,d=1,2,…,D;k为当前的迭代次数;w为惯性权重;c1和c2分别为个体学习因子和群体学习因子,典型值取c1=c2=2;r1和r2为0～1的随机数。

2.2 改进的粒子群算法

在标准的PSO算法中,需要输入重复的数据进行迭代寻优,显然这不符合ANC系统实时运行、逐点采样噪声的特点,因此标准的PSO算法不能直接在ANC系统中使用。本文对于标准PSO算法做了如下改进:为了与实时ANC系统相配合,在每个采样时刻仅使用一个粒子作为关键参数参与ANC系统的运算,该粒子连续使用L个采样时间后计算粒子的适应值,并随机不重复地选择下一个粒子作为关键参数。对于粒子总数为N的种群,完成一轮粒子群迭代总共需要经历N×L个采样输入信号。通过以上方法,确保了ANC系统和粒子群都能在线实时更新,其中ANC系统是逐个噪声采样点更新,粒子群算法是逐个数据块(N×L个采样点)进行更新。标准的粒子群算法在每一轮迭代中需要相同的输入数据,而提出的改进算法是伴随噪声采样实时更新粒子,这是本文提出算法与标准算法最大的不同。

为了获得更好的寻优表现,本文还对PSO算法做了以下的改动。

(1)引入线性微分递减的惯性权重调整策略。从公式(1)中可以看出,惯性权重w代表上代粒子对当代粒子速度的影响。本文引入了以下线性微分递减的w调整策略,保证PSO算法在迭代前期使用较大的w,充分发掘可能的最优解,而在后期使用较小的w,提高局部搜索能力,保证寻优精度[8]。

(3)

其中,wmax和wmin分别代表惯性权重的最大值和最小值,分别取0.9和0.4;tmax和t分别代表最大迭代次数和当前迭代次数。

(2)鲁棒的适应度函数。脉冲噪声是ANC系统中常见的噪声源,由于含有较多的异常值,因此容易造成算法的发散。在使用粒子群在线估计参数时,同样要考虑脉冲噪声对粒子群寻优的影响。为了增强粒子群应对脉冲噪声的能力,采用如下鲁棒性更强的适应度函数:

(4)

其中,L代表连续的L个误差信号采样点,tanh(·)代表双曲正切函数,e(i)为误差信号。通过对误差信号做非线性压缩变换,从而消除异常值的不利影响。

2.3 改进PSO用于ANC算法参数在线估计

为了展示改进PSO算法在ANC系统中的应用效果,将提出算法应用于FxMCC-MK算法关键参数的在线估计[9]。FxMCC-MK算法的ANC控制器权系数更新公式如下:

(5)

λ(n)=1-exp(-βe2(n))

(6)

w(n)为n时刻滤波器权系数,e(n)为误差信号,xf(n)为滤波后的参考信号,λ(n)为混合参数,sign(·)为符号函数。步长μ、核宽σ及λ(n)的形状调整参数β均属于超参数,对于算法的降噪表现起着关键作用,这里使用提出的改进PSO算法将参数在线更新为“正确”值。基于改进PSO的FxMCC-MK算法的系统框图如图2所示,其中d(n)为需要抵消的噪声信号,y(n)为ANC控制器输出信号,yf(n)为y(n)经过次级路径后的信号,e(n)为误差信号。

图2 基于改进PSO的FxMCC-MK算法系统框图Fig.2 System block diagram of FxMCC-MK algorithm based on modified PSO

基于改进PSO的FxMCC-MK算法的主要执行流程如下。

步骤1:设置PSO算法关键参数,包括粒子群规模N,粒子维度D,数据块长度L,最大迭代次数K等;并随机初始化粒子位置和速度。初始化的粒子群如下:

(7)

步骤2:随机不重复地从种群中选择粒子作为FxMCC-MK算法的关键参数,并通过公式(5)和公式(6)更新控制器系数。每个粒子在L个采样时刻内连续使用,所有粒子完成该步骤需要经历N×L个采样时间。

步骤3:完成L个采样后,使用公式(4)计算粒子的适应值,并记录当前粒子的位置和个体最优位置;当步骤2重复一轮后,比较所有粒子的个体最优位置获得群体最优位置。

步骤4:根据公式(3)更新惯性权重ω,并根据公式(1)和公式(2)更新所有粒子的速度和位置。

步骤5:判断是否满足算法的停止条件,如果满足则停止粒子群更新,将最终获得的gbest作为最优的参数,供ANC系统继续运行,如果不满足条件,则返回步骤2继续优化参数。

3 算法的计算性能分析(Performance analysis of the algorithm)

本文提出的改进PSO算法利用随机、分块选择更新粒子,实现了ANC系统关键参数的在线匹配。但不可否认,改进PSO算法的引入增加了实时降噪系统的计算负担,增加的计算量见表1。从表1中可以看出,额外增加的计算量不容忽视。为了降低计算负担,种群粒子总数N和数据块长度L都不应过大。当控制滤波器长度P和次级路径长度M较大时,则增加的计算量可以相对忽视。除此以外,改进PSO具有在线迭代寻优的特点,相比直接使用一组较好参数,使用PSO寻优的ANC算法在收敛速度上并不具有优势,这点能在仿真中体现。需要注意的是,为了保证算法能快速收敛到最优位置,应当通过经验数据给出粒子位置的大致范围。

表 1 改进PSO算法引入的计算量

4 仿真与分析(Simulation and analysis)

在计算机仿真中,将控制滤波器的长度设置为20,ANC系统的初级路径P(z)和次级路径S(z)分别设置如下:

P(z)=0.05z-13-0.01z-14+0.01z-15+0.8z-16+0.6z-17-

0.2z-18-0.5z-19-0.1z-20+0.4z-21-0.05z-22

(8)

S(z)=0.05z-6-0.01z-7+0.95z-8+0.01z-9-0.9z-10

(9)

采用平均噪声衰减量(ANR)评价算法的降噪表现,ANR按如下公式定义[9]:

(10)

(11)

其中,Ae(·)和Ad(·)的初始值均为0,η是遗忘因子,一般取0.999。

仿真中使用服从标准对称α稳定(Symmetric α-Stable, SαS)分布的数据模拟脉冲噪声[6],SαS分布的特征函数如下:

φ(n)=exp(-|t|α)

(12)

其中,α为特征指数,α∈(0,2],α越小,生成的数据脉冲性越强,图3为α=1.6时的脉冲噪声信号。仿真中粒子群的基本设定为粒子群规模N=20,数据块长度L=20,最大迭代次数K=50,粒子维度D与ANC算法关键参数个数一致。

图3 α=1.6时生成的脉冲噪声信号Fig.3 Impulse noise signals generated at α=1.6

首先,在ANC系统中,分别使用改进PSO在线匹配参数和试错法精确指定参数,比较不同方式下FxMCC-MK算法的降噪表现,参考噪声采用α=1.6的脉冲噪声信号。改进PSO算法关键参数的寻优范围为μ∈[1e-4,1e-3]、σ∈[1,10]、β∈[0.1,1]。图4为改进PSO在线匹配ANC参数的收敛曲线,从图4中可以看出,改进PSO算法快速收敛,大约在20轮迭代后即能找到最优解,获取到的最优参数值为μ=5.807 6e×10-4,σ=4.966 1,β=0.512 3。改进PSO和试错法的降噪效果对比如图5所示。case1为通过试错法反复实验得出的最优参数组合,case2～4在case1参数的基础上有略微改动。从图5中可以明显看出,case1同时兼顾了收敛速度和稳态误差,降噪效果可以认为是最好的。在case2～4中,参数发生改动后,算法的降噪效果也相应受到影响,如果参数改动较大,甚至可能导致算法不收敛或者失稳。相比case1,改进PSO算法收敛速度略慢,但是获得了更低的稳态误差值。以上结果表明,改进PSO算法能够快速在线获取最优参数,虽然ANC系统的收敛速度会略微降低,但是降噪效果会得到提升。

图4 改进PSO匹配ANC关键参数的收敛曲线Fig.4 The convergence curve of modified PSO matching ANC key parameters

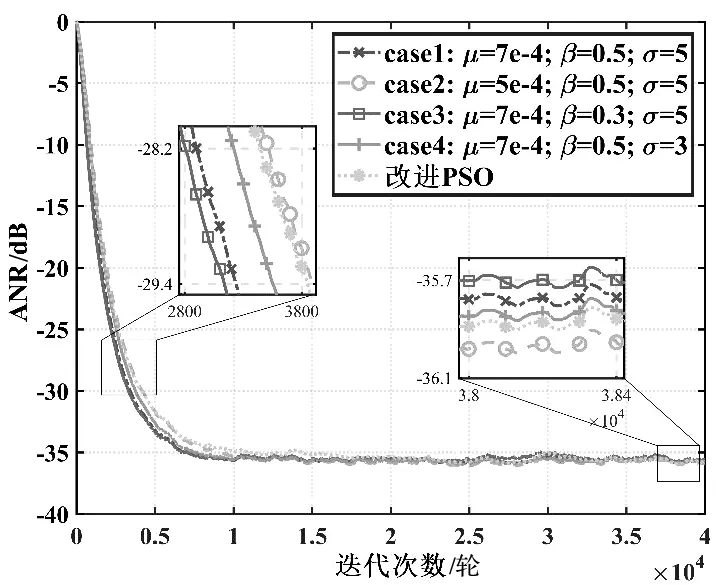
图5 改进PSO与试错法的ANR对比Fig.5 Comparison of ANR between modified PSO and trial and error method

其次,将使用改进PSO的FxMCC-MK算法与常见ANC算法进行降噪性能对比分析,参与对比的另外三种算法分别是滤波-x最小P范数(FxLMP)算法、基于sigmoid变换的FxsigmoidLMS算法和基于对数变换的FxlogLMS算法,新引进的三种算法的特点为参数只有步长μ,比较容易通过试错法确定最优值[10-12]。不同算法的降噪效果如图6所示,从中可以看出直接使用试错法的FxMCC-MK算法在收敛速度上具有绝对优势,使用改进PSO的FxMCC-MK算法收敛速度略慢于直接使用试错法,但与FxsigmoidLMS算法相近,明显优于FxLMP算法和FxlogLMS算法。此外,FxMCC-MK(改进PSO)算法的稳态误差值是最低的,稳定值为-35.6 dB。由此可见,通过改进PSO在线匹配关键参数,虽然会略微降低FxMCC-MK算法本身的收敛速度,但是整体上该算法的降噪性能仍然要优于其他三种算法。

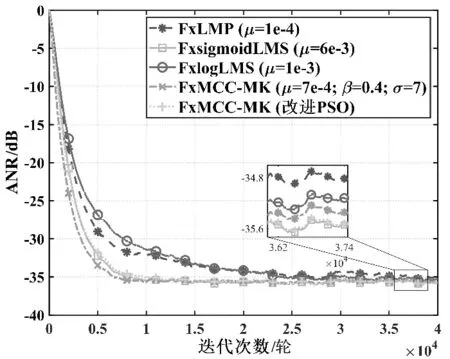
图6 与常见ANC算法降噪效果对比Fig.6 Comparison of noise reduction effect with common ANC algorithm

5 结论(Conclusion)

本文提出了一种用于在线获取ANC系统关键参数的改进PSO算法,该算法通过在降噪过程中随机选择粒子,并作为关键参数用于降噪系统的运行,算法以数据块为单位进行粒子群的迭代更新,实现了PSO参数寻优与实时ANC系统的同步运行。此外,引入了线性微分递减的惯性权重调整策略,保证了算法的寻优能力;使用非线性的双曲正切函数压缩异常的噪声信号,增强了适应度函数的鲁棒性。未来,将提出的改进PSO框架用于FxMCC-MK算法关键参数的在线寻优中,并分析增加的计算负担。实验结果表明,改进PSO算法能够实现关键参数的快速寻优,并且保持了ANC系统优秀的降噪能力,在实际应用中具有潜在的价值。