液化天然气中CO2的溶解度计算新方法
2023-08-08蔡伟华王照曦段欣悦花亦怀车勋建
蔡伟华 高 磊 王照曦 段欣悦 边 江 花亦怀 车勋建
1. 东北电力大学能源与动力工程学院 2. 中国石油大学(华东)储运与建筑工程学院 3. 中海石油气电集团技术研发中心
0 引言
近年来,全球天然气需求的迅速增长促使海上天然气的利用成为能源发展的重要方向。不同于传统的陆基天然气供应,海上(尤其是深远海)天然气的开采、运输工作环境恶劣、工作空间狭小,对技术方案的占地面积、安全性等提出了更高的要求。因此,液化天然气技术是深远海天然气利用最为可行的技术方案。
天然气液化前需净化除去许多杂质气体,比如CO2、H2S等。在天然气液化过程中,随着温度的降低,CO2易形成晶体析出,造成管道和设备堵塞,严重影响液化进程。传统常压液化工艺(-162 ℃)对天然气中CO2含量有着严格的限制,即允许含量(摩尔分数)不超过0.01%。带压液化天然气(PLNG)技术,即通过提高液化天然气储存压力,进而提高液化温度(-100~-120 ℃),最终实现提升液化天然气中CO2溶解度的目的[1-3]。由于PLNG技术大大增加了LNG中CO2的溶解度,使得天然气预处理环节对CO2脱除率的要求大大降低,从而可大幅减少海上液化天然气中液化工艺设备和甲板空间。因此,液化天然气中CO2的溶解度,是设计海上天然气预处理工艺和判断液化工艺对原料气适应性的重要依据。
国内外学者采用实验测定、理论计算和软件模拟的方法开展了CO2的溶解度相关研究。例如,通过固液相平衡实验,获得部分低温条件下CO2在液态甲烷(CH4)中的溶解度[4-8],其中Donnelly等[4]对CO2—CH4二 元 混 合 物 在194.54~215.37 K温度范围内的固液气三相点进行实验测定,并根据固液相平衡数据对相图进一步分析,得到一定温度和CO2浓度范围内任何压力下都不会形成固相的结论。Davis等[5]通过实验测定CO2—CH4二元混合物的固液气三相点和液相成分,得到在129.65~201.26 K温度范围内CO2在液态CH4中的溶解度。Preston等[6]通过实验测定90.00~125.00 K温度范围内CO2和部分碳氢化合物在液态CH4和Ar中的溶解度。沈淘淘等[7]在更广泛的温度区间得到CO2在液态CH4和CH4—N2/C2H6中的溶解度实验数据,并根据实验数据对二元交互作用系数进行拟合,提高了理论计算CO2在液态CH4中溶解度的准确性。
由于相平衡实验较为复杂,且实验数据不连贯,部分学者采用理论计算和软件模拟开展CO2在CH4等中的溶解度研究。胡晓晨等[9]采用HYSYS软件预测CO2晶体析出温度,并对影响CO2溶解度的组分、温度等因素进行分析,发现CO2溶解度随储存温度的降低而降低的结论,同时在153.00~163.00 K温度范围内随着温度升高,CO2在液态CH4中的溶解度出现两次较大幅度的增加,但该结论缺少实验数据验证。沈淘淘等[10]在理想溶液的基础上,采用正规溶液关系式、修正的Scatchard—Hildebrand关系式和HYSYS软件,对CO2在饱和液态CH4中的溶解度进行计算,证实了在低于160 K温区,采用改进的正规溶液理论方法,其计算结果与实验结果最接近,但在温度较高时,计算误差仍偏大。此外,部分学者关注CO2析出温度,从另一个角度研究CO2的析出。蒋洪等[11]通过使用Peng—Robinson(PR)状态方程法和HYSYS软件,分别对液固相平衡和气固相平衡中的固体CO2形成温度进行计算,认为PR状态方程法的计算误差明显小于采用HYSYS软件的计算误差。孔令伟[12]通过拟合关联式,给出CH4—CO2二元系中CO2固体形成温度的预测模型,发现该模型计算结果与Kurata[13]实验数据的平均偏差在1℃以内。
上述研究中,采用实验方法得到的CO2溶解度数据较少,并且测定结果受限于温区,与实际天然气液化工况吻合的较少。通过理论计算和软件模拟得到的CO2溶解度在一定温区内具有较高准确度,但在天然气液化过程的宽温区内,无法保持同样的准确度。HYSYS计算多集中于CO2析出温度的相关研究,对CO2在液化天然气中的溶解度计算研究较少。因此,笔者使用HYSYS软件和理论自编程法计算了液化天然气中CO2的溶解度,并通过分温区拟合二元交互作用系数,来提高两种计算方法在较宽温区的准确度和对溶剂组分的适用性。
1 计算方法
溶质在低温溶液中的溶解度与其相变过程密切相关,图1是根据HYSYS软件计算结果绘制的CO2—CH4二元系p—T图。图中给出了CO2—CH4二元组分在不同CO2含量下对应的露点线、泡点线和结晶线。图中右下方为CO2和CH4二元系的气相区,随着温度的降低和压力的升高,气相混合物通过露点线进入气液两相区。压力继续升高和温度继续降低时,气液两相混合物通过泡点线后进入液相区。在液相区内,继续降低液相混合物的温度,混合物状态点到达结晶线时,会析出CO2固体,此时液相中的CO2含量达到饱和,即当前温度下CO2在液态甲烷中的溶解度。CO2在多元组分中的析出过程与之类似,溶解度计算可根据固液相平衡原理进行。
文献[8]利用图论与矩阵理论证明了编队控制一致性的可实现性,为基于一致性理论的多智能体系统编队控制研究奠定了基础.Saber等[9]首次考虑时延情形,开展了连续时间多智能体系统编队控制一致性问题的研究.而后,Lin等[10]研究了通信拓扑切换情况下,时延多智能体系统的编队控制一致性问题.

图1 CO2—CH4二元系溶液的p—T相图
1.1 HYSYS软件
HYSYS软件是一款在石油、天然气等化工领域广泛应用的大型系统软件,具有很高的可信度[14]。使用HYSYS计算CO2的溶解度时,选择PR状态方程作为物性计算方程,采用表1中软件默认的各组分间二元交互作用系数(kij)进行计算。通过创建物流、输入物流的气相分数、温度和组分比例,进行物流参数计算。采用CO2Freeze Out工具包来计算已知参数的物流在此时工况下CO2的结晶温度,然后通过改变CO2的摩尔分数使得结晶温度与输入温度相等,此时得到的CO2摩尔分数即为输入温度下CO2在物流中的溶解度。
师:接下来,我们要写的就是小动物吃东西的样子,先看看作者是怎么写“黑脸琵鹭”吃东西的过程。在介绍黑脸琵鹭的捕食时,作者运用了丰富而精准的动词,将捕食的画面带到读者面前,也很吸引人。想一想,你喜欢的那种动物,他是怎么吃东西的呢?

表1 HYSYS计算中不同组分间的kij值表
1.2 理论自编程法
纯物质的逸度系数不需要使用混合规则,所以CO2固体的逸度系数为[16]:
由于PR状态方程[16]结合经典的VDW混合规则[17],已被广泛应用于天然气系统的相关计算,因此选择其标准形式来进行固液相平衡计算。该方程可表示为[16]:
在液相混合物中,CO2的逸度系数为[16]:
港口城市以发展经济为导向投资港口时,无论Y市投资多少,D市的投资回报率都高于9.59%,因此会以最大能力投资港口市投资能力<40亿元时,Y市的港口投资回报一直低于城市平均投资回报(8%),此时他显然没有投资港口的意愿,不会投资港口市投资能力>40亿元,其港口投资回报率>8%,他会以最大投资能力投资。
式中Z表示压缩因子;
参考ZareNezhad等[18]根据本文参考文献[21-22]的推导结果,提出一种与温度有关的kij表达形式:
过去的数学课堂教学,因为受到应试教育的影响,特别强调对规律、理念等既定知识的把握,同时经过广泛的应用与练习给予加强,而忽略指引学生对知识产生经过的分析与感受,具有相对普遍的“重视结果轻视过程”状况。实际上,在认识与探索知识的产生与发展过程当中,学生学习到的是处在水平关键地位的普遍方式,并且在这个过程当中,学生体会到的是不断建设新知识体系的乐趣。对于学生而言,这就是一种创造。应该精准地掌握知识产生发展的经过,这要求教师不应该只深入钻研课本的内在机制,还应该仔细探索学生的学习想法,应该寻求到知识逻辑与学生内心的逻辑默契之处[2]。
式中xi和xj分别表示混合物中组分i和j的摩尔分数;kij表示组分i和组分j的二元交互作用系数;Tci表示组分i的临界温度,K;pci表示组分i的临界压力,kPa;ωi表示组分i的偏心因子。
解决策略:找出中心主题“干旱的不同阶段”,再找其余关键词(关节点),并以新的关键词为起点再向外发散,画出逻辑流程图(图4),本质之间的关系理清后,自然就能答出完整的答案,提高说理题的复习效率。学生将分析的过程和易错的环节记录、固定下来,再次复习时,见图就能再现当时的思维过程,大大降低了再次出错的概率。
CT检查结果按照直肠外壁光滑度,脂肪密度等对肿瘤侵犯程度进行评价。之后将患者MRI和CT检查结果与手术病理检查结果进行比较。
式中ZL表示在压力为p和温度为T时,混合物中液相CO2的压缩因子。
根据相平衡原理,系统达到固液平衡时 CO2在固相和液相中逸度相等,此时 CO2液相的摩尔分数(xCO2)可表示为:
Wade:Yeah, Wade, Z. You can call me whatever you want. I’ll call you Sam.
式中ZV表示纯 CO2气体在压力和温度T时的压缩因子。其中= exp (-3 108.2 /T+ 20.665 4 ),为本文参考文献[18-19]拟合的CO2气固饱和蒸汽压函数。
由于以上求解过程较复杂,无法直接求解,因此采用二分法进行数值求解。表2为各组分间的二元交互作用系数,其中kCO2—CH4使用ZareNezhad[18-19]拟合的函数,其他二元交互作用系数使用HYSYS软件中默认的二元交互作用系数。计算中所用的各组分物性参数如表3所示。
民乐铜矿样品中的安山岩轻重稀土分异非常明显,其ΣREE介于114.20×10-6~119.29×10-6之间。矿区玄武岩也基本上都在123.96×10-6-202.09×10-6之间(李学军,2009)。

表2 理论自编程法计算中不同组分间的kij值表

表3 各组分物性参数表
2 计算结果和讨论
采用HYSYS软件和理论自编程法分别计算了不同温度下CO2在CH4—CO2二元系溶液、CH4—CO2—N2和CH4—CO2—C2H6三元系溶液中的溶解度,并与文献中的实验数据进行对比分析。通过优化关键参数,有效提高CO2溶解度的准确度,提升了计算方法对溶剂组分的适用性。
2.1 CO2在CH4—CO2二元系溶液中的溶解度
以本文参考文献[7]中CO2溶解度实验数据为基准,采用HYSYS和理论自编程法分别计算110~170 K温度范围内CO2在液态CH4中的溶解度,计算结果和相对误差如表4所示。
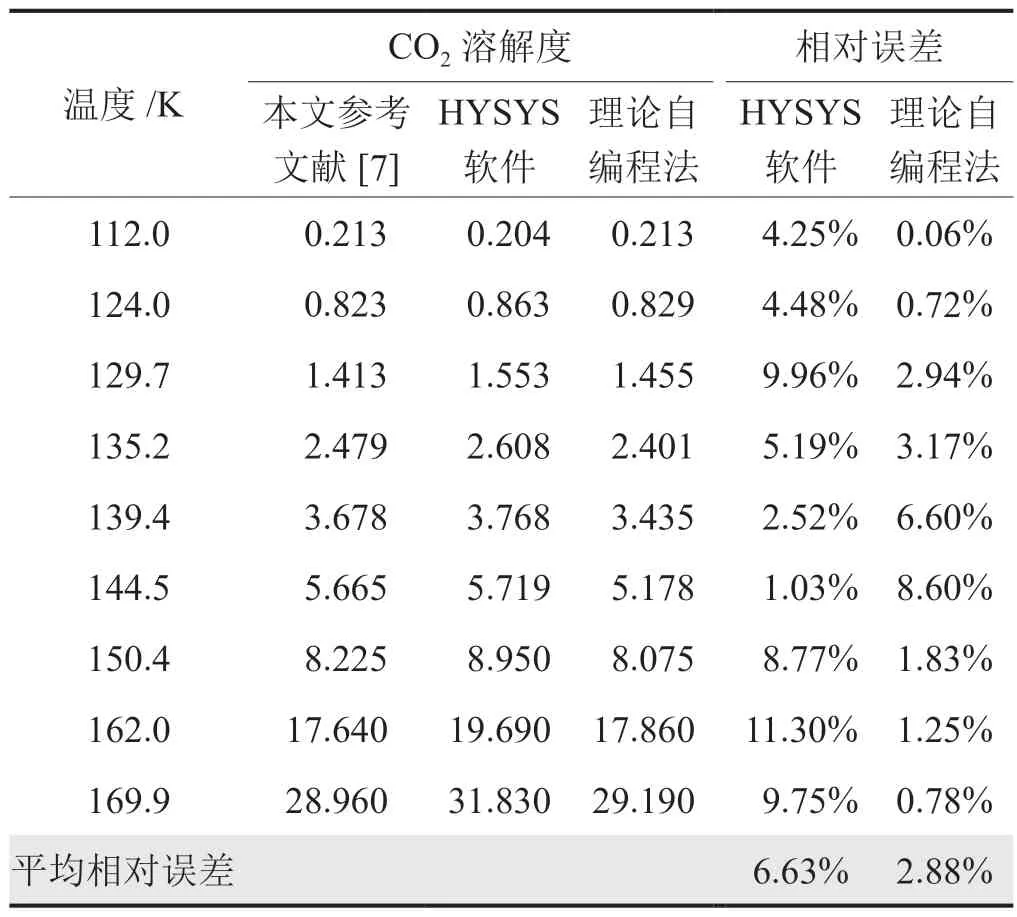
表4 CO2在CH4—CO2二元系溶液中的溶解度(xCO2×103)及相对误差表
比较文献实验数据与两种方法所得的CO2溶解度数值,可以发现,对CH4—CO2二元系溶液而言,采用HYSYS和理论自编程法计算的平均相对误差分别为6.63%和2.88%。因此,理论自编程法计算结果与实验数据的误差更小。
2.2 CO2在CH4—N2—CO2三元系溶液中的溶解度
天然气中包含多种组分,氮气是其中比较常见的一种组分。分别采用HYSYS软件和理论自编程法计算CO2在摩尔分数依次为98% CH4+ 2% N2、95% CH4+ 5% N2、90% CH4+ 10% N2不同配比混合溶剂中的溶解度,并与本文参考文献[7]中不同对应温度下的实验数据进行对比。计算结果和相对误差如表5、6所示。
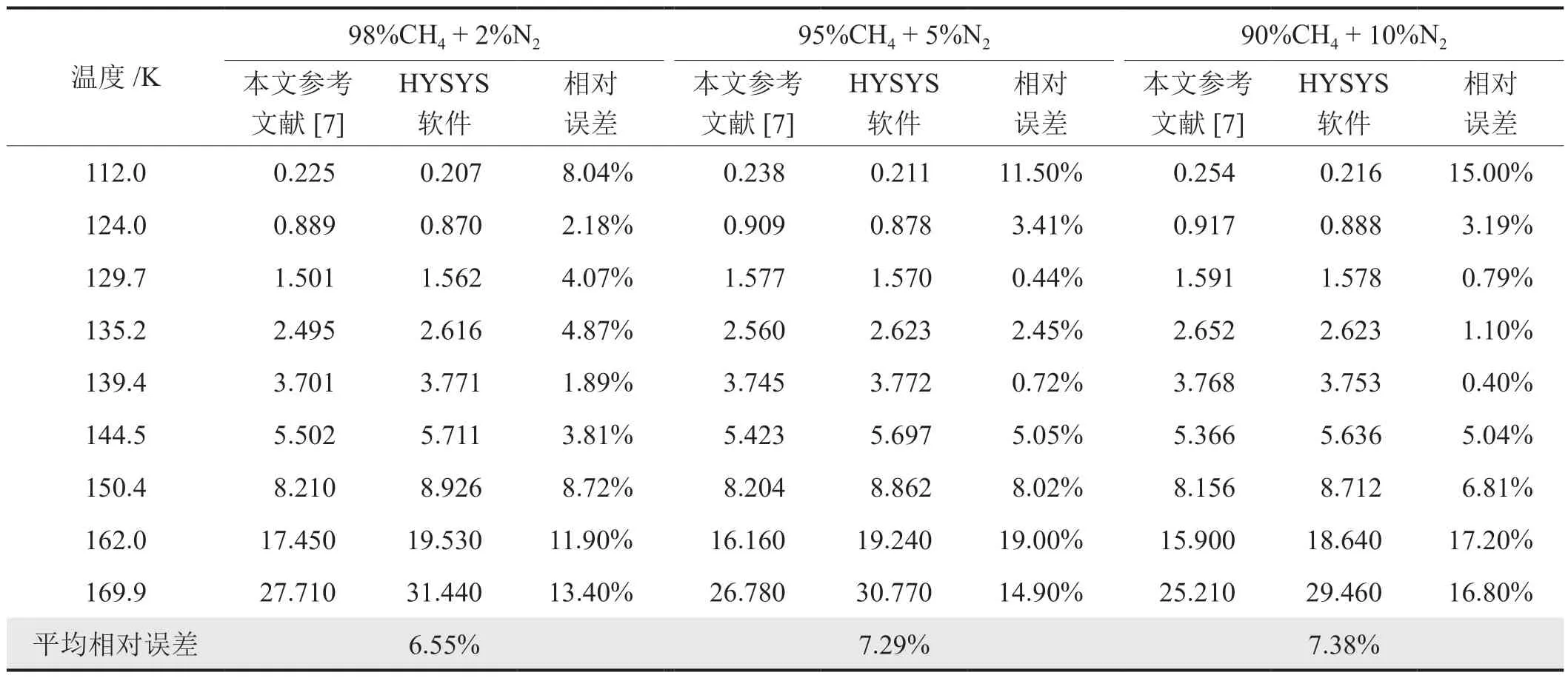
表5 HYSYS计算的CO2在CH4—N2—CO2三元系溶液中的溶解度(xCO2×103)及平均相对误差表

表6 理论自编程法计算的CO2在CH4—N2—CO2三元系溶液中的溶解度(xCO2×103)及平均相对误差表
在表5、6中,对CH4—N2—CO2三元系溶液进行计算时,HYSYS软件计算的平均相对误差分别为6.55%、7.29%和7.38%。理论自编程法计算的平均相对误差则为3.30%、4.39%和3.76%。因此,理论自编程法计算值与文献实验数据更吻合,具有更高的准确度。
1)潞新矿区实体煤巷道强矿压显现及大变形原因为卸载和冲击载荷的双重作用引起煤层似层裂、劈裂并不断扩展导致的剪胀变形。
2.3 CO2在CH4—C2H6—CO2三元系溶液中的溶解度
乙烷在实际天然气组分中占比也较高。因此,采用同样的计算方法分别计算不同温度下CO2在摩尔分数依次为98% CH4+ 2% C2H6,95% CH4+ 5% C2H6,90% CH4+ 10% C2H6这3种不同配比的混合溶剂中的溶解度,并与本文参考文献[7]中的实验数据进行对比。计算结果和相对误差如表7、8所示,结果表明对CH4—C2H6—CO2三元系溶液进行计算时,HYSYS计算的平均相对误差分别为4.78%、5.29%和6.81%;理论自编程法计算的平均相对误差分别为3.62%、2.56%和3.65%。
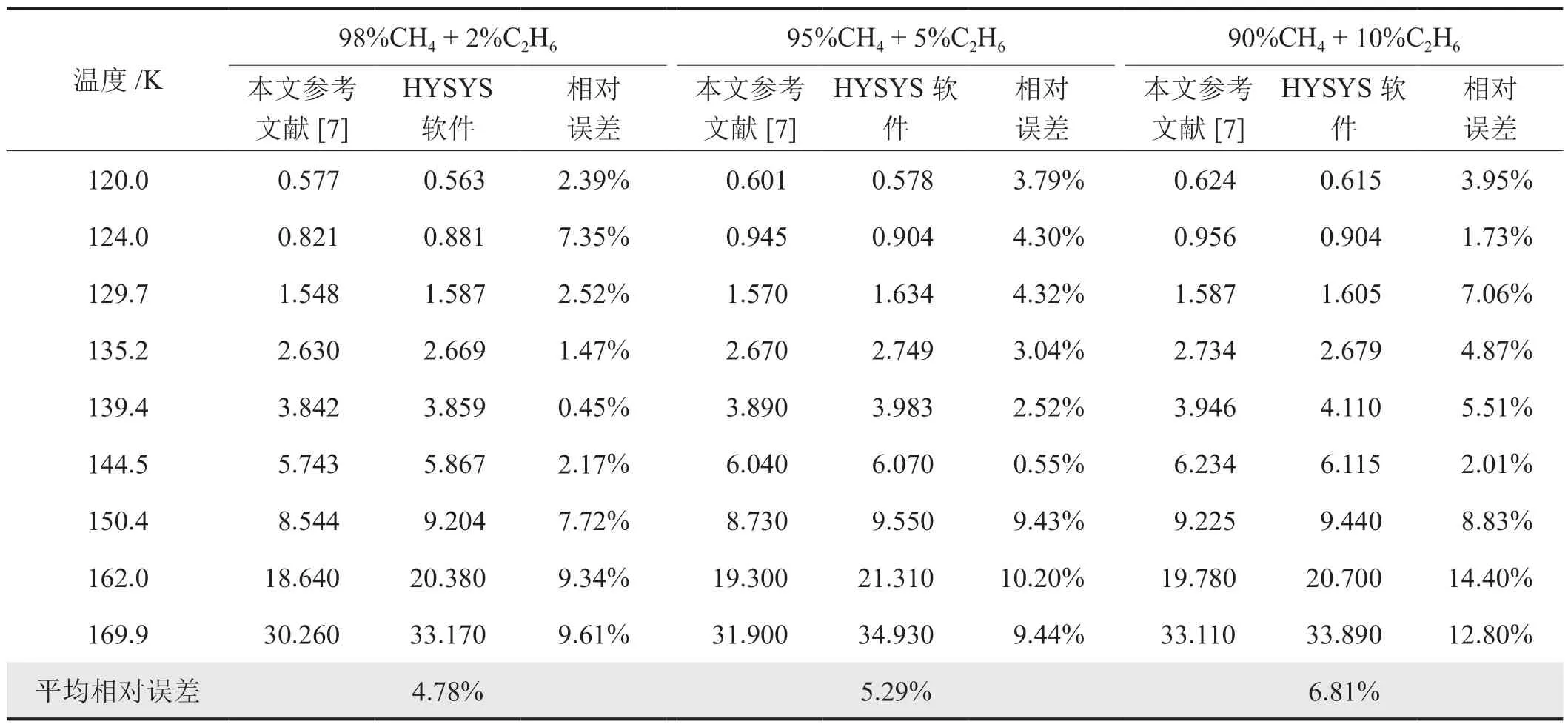
表7 HYSYS软件计算的CO2在CH4—C2H6—CO2三元系溶液中的溶解度(xCO2×103)及平均相对误差表

表8 理论自编程法计算CO2在CH4—C2H6—CO2三元系溶液中的溶解度(xCO2×103)及平均相对误差表
对比两种方法在三元系溶液中CO2溶解度的计算误差,理论自编程法计算结果与实验数据更吻合,具有更高的准确度。究其原因,与两种计算方法采用不同的CH4—CO2的二元交互作用系数有关,其中,HYSYS软件计算时使用系统默认的二元交互系数,而理论自编程法计算则使用本文参考文献[18-19]中拟合的随温度变化的二元交互作用系数函数。
2.4 二元交互作用系数的影响
二元交互作用系数kij是表征两种分子i和j之间相互作用的特性参数,反映了分子之间的相互作用及非理想作用性质。为提高溶解度计算的准确度,从实验数据中得到准确的kij数值,并利用最小二乘法分别针对HYSYS软件和理论自编程法计算提出更为适用的kij。
VDW混合规则[17]:
焦虑主要指对某种尚未发生的事情所产生一种忐忑不安、不愉快的情绪体验,常伴有紧张、出汗、恐惧、不安等症状;抑郁主要指自己感觉心情沉重,产生绝望、无助、无用等感受,且伴有兴趣缺乏、乐趣丧失、疲倦懒散等症状。
在CH4—CO2二元体系下,采用PR状态方程进行计算时,在室温下的二元交互系数为0.1[23],因此,取a0为0.1,根据溶解度实验数据进行反推,得到不同温度下与两种计算方式分别对应的理想二元交互系数k12,然后借助最小二乘法拟合得到a1和a2的值。其中,在不同温度下CO2溶解度的HYSYS计算值与文献实验数据相对误差小于0.5%时对应的k12,记为HYSYS计算对应的理想k12,理论自编程法计算值与文献实验数据相对误差小于0.5%时对应的k12,记为理论自编程法计算对应的理想k12。
根据不同温度下的理想k12数值,采用最小二乘法分别拟合适用于HYSYS软件和自编程计算的二元交互系数,结果如图2、3所示。由图2、3可见,采用全温区拟合确定的二元交互系数,与理想k12偏差较大,采用分温区拟合二元交互系数在整个温区与理想k12更为接近。因此,采用分温区拟合的方法来确定CO2与CH4的二元交互作用系数,拟合式如表9所示。

表9 HYSYS计算和理论自编程法计算各自适用的二元交互系数的拟合式统计表

图2 HYSYS计算适用的二元交互系数图

图3 理论自编程法计算适用的二元交互系数图
为验证二元交互系数拟合式的准确度,分别采用HYSYS软件和理论自编程法计算,使用分温区拟合的二元交系数来计算CO2在液态CH4中的溶解度,计算结果如表10所示。由表10可知,HYSYS计算值与文献实验值的平均相对误差为1.69%,而理论自编程法计算值与文献实验值的平均相对误差也仅为1.75%。两种计算的平均相对误差都有一定的减小,尤其是HYSYS法,其平均相对误差从6.63%降到1.69%,准确度大幅提升。
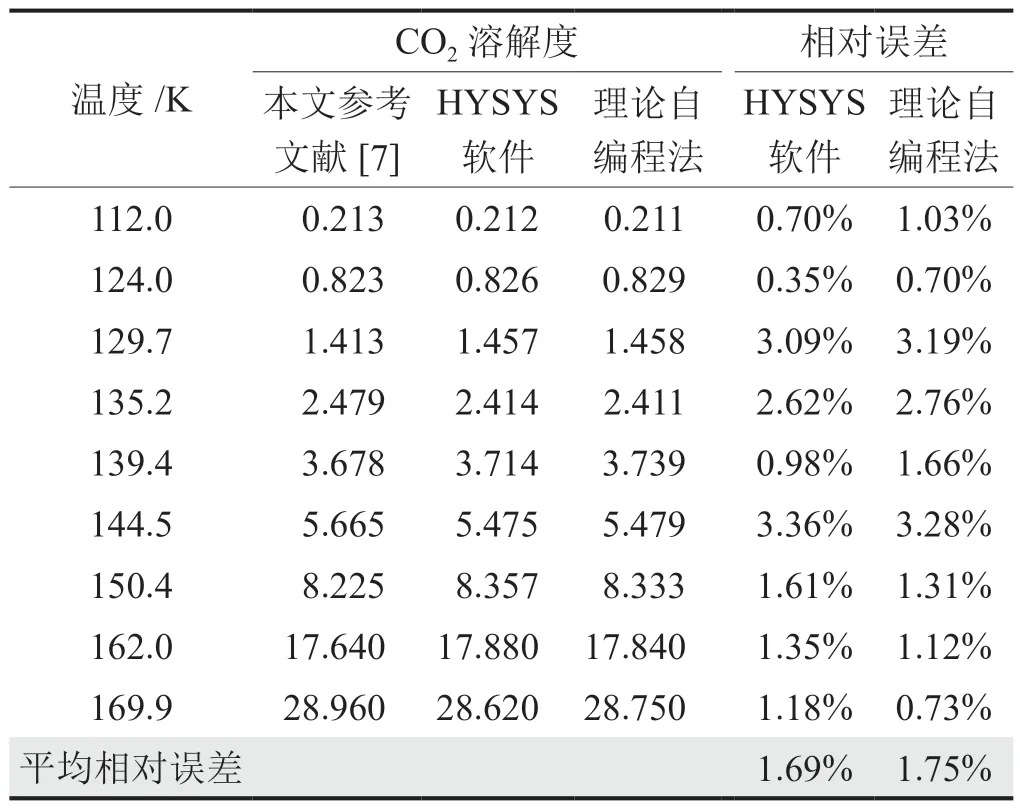
表10 CO2在CH4—CO2二元系溶液中的溶解度(xCO2×103)及相对误差表
为进一步研究在三元系溶液中,使用分温区拟合的二元交互系数来计算CO2溶解度的准确度,分别使用HYSYS软件和理论自编程法分别计算CO2在CH4—N2—CO2和CH4—C2H6—CO2三元系溶液中的溶解度,计算结果如表11、12所示。
表11 CO2在CH4—N2—CO2三元系溶液中的溶解度(xCO2×103)及平均相对误差表

表12 CO2在CH4—C2H6—CO2三元系溶液中的溶解度(xCO2×103)及平均相对误差表
为更直观地对比分析使用分温区拟合二元交互作用系数的效果,图4、5分别给出了HYSYS软件和理论自编程法计算三元系中CO2溶解度结果与文献实验数据的平均相对误差。从图4、5可以看出,使用实验数据分温区拟合二元交互作用系数,均提升了CO2溶解度的准确度。同时,随着N2/C2H6含量增加,相应计算值与文献实验数据的平均相对误差也随之增加。这是因为N2/C2H6对CO2和CH4的二元交互作用系数在HYSYS软件和理论自编程法计算中均为常数值,而实际二元交互系数是会随着工况改变而变化的。当N2/C2H6含量少时,对计算结果影响不大,随着N2/C2H6含量升高,这种影响会愈加明显,从而导致在N2/C2H6含量较高时,两种方法的计算值与实验数据的偏差增大。由此可见,二元交互作用系数对整个相平衡的计算有着重要影响,准确的二元交互作用系数,可根据实验数据回归分析获得。由于N2/C2H6高浓度的三元系溶液相关实验数据十分有限,目前只对CH4—CO2的二元交互作用系数进行了分温区拟合研究,相应的其他组分与CO2的二元交互系数研究仍有待完善。
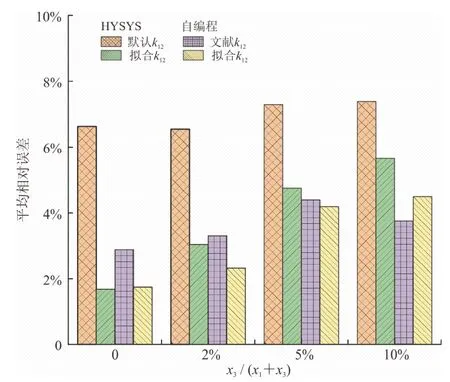
图4 CH4—N2—CO2三元系溶液中平均相对误差图
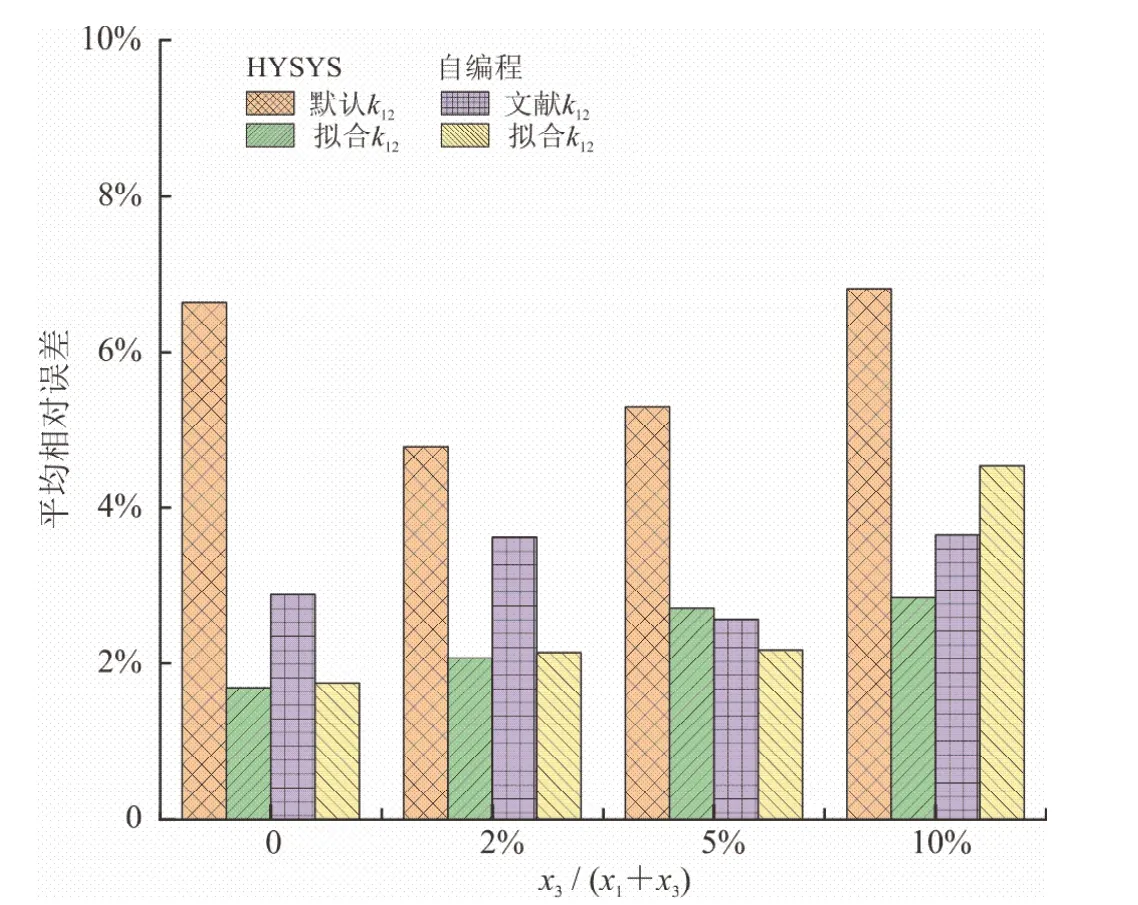
图5 CH4—C2H6—CO2三元系溶液中平均相对误差图
3 结论
1)两种方法的计算结果与实验数据的平均相对误差均小于8%,且理论自编程法计算CO2的溶解度比HYSYS软件计算结果具有更高的准确度。
2)使用分温区拟合的CH4—CO2二元交互作用系数后,提升了HYSYS软件和理论自编程法对CO2溶解度的计算准确度,同时提高了溶解度计算方法对组分的适用性。
3)两种方法计算的平均相对误差随N2/C2H6含量的增加而增加。液化天然气中N2/C2H6的含量较少,使用分温区拟合的CO2、CH4二元交互作用系数后两种计算方法均可满足工程计算要求。
4)为进一步提升CO2溶解度计算的准确度,有必要对其他组分与CO2的二元交互系数开展深入研究。
