具有梯度静应力的红砂岩应力波衰减特性试验研究

金解放，刘康，张雅晨，王熙博，张睿，石子勃，徐虹

(1.江西理工大学 土木与测绘工程学院，江西 赣州，341000；2.江西理工大学 资源与环境工程学院，江西 赣州，341000)

在地下工程岩体爆破开挖过程中，赋存在不同地应力环境下的围岩体受到动荷载作用，动荷载产生的应力波在不同地应力环境下的工程岩体中传播衰减。由于深部岩体构造应力的复杂性以及开挖卸荷导致原岩应力重分布，径向应力在围岩孔洞边界附近呈现不同且明显的梯度变化[1-5]。梯度的径向地应力导致围岩体具有不同的孔隙度或损伤程度，影响爆破应力波在围岩体中的传播衰减特性。研究爆破应力波在具有特定地应力环境下的岩石中传播的衰减特性及其影响机理，对完善应力波传播理论、评估围岩及邻近建(构)筑物的稳定性具有重要的理论指导意义。

深部围岩体在爆破开挖时，爆破应力波产生的能量一部分于工程岩体的破碎过程中耗散，另一部分以应力波的形式在围岩体中传递。应力波在具有复杂地应力环境的围岩体中传播衰减，地应力会影响岩石(体)的孔隙度、损伤程度、波阻抗等，进而控制应力波在工程岩体中的传播衰减特性，因此，地应力是影响岩石(体)应力波传播衰减特性的重要因素[6-7]。目前，众多学者对均匀应力对应力波传播衰减特性的影响进行了研究。对组合煤岩短试件进行应力波传播试验[8]，得到应力波波形、透反射系数、能量耗散等应力波传播表征量随轴向均匀应力的变化规律。通过对轴向均匀应力作用下的红砂岩长试件[9]进行应力波传播试验，发现随着轴向均匀应力的增加，应力波纵波波速呈“快速增加—平缓发展—急剧减小”的趋势，轴向均匀应力下的应力波幅值随传播距离与传播速度增大都呈指数衰减。应力波纵波波速、波幅等参数对静应力的敏感性与初始孔隙的闭合和微裂纹的萌生和扩展密切相关，考虑孔隙度和损伤演化从本质上解释了轴向均匀应力对应力波传播衰减特性的影响[10]。在充分认识到地下围岩体处于梯度应力环境后，袁伟等[11-12]提出了能够施加径向梯度应力的试验方法并设计了试验装置，但关于具有梯度静应力工况下岩石应力传播衰减特性没有进行系统研究。

在时域内，应力波的幅值、纵波波速、透反射系数及能量耗散等是表征应力波衰减规律的重要参数[13-15]。在频域内，可将任意形式的波信号分解为不同频率的谐波分量。在实际工程中，爆破振动的频率特性也是爆破施工的安全判据之一[16]。在爆破工程中，范磊等[17-19]对时域波形数据进行了快速傅里叶变换，将振动波信号在频域内进行了分析。应力波各谐波分量随频率的变化是时域波形中应力波幅值、波速等衰减的内在原因[20]，进一步分析爆破应力波主频和质心频率的变化有助于更好地了解岩石应力波的传播衰减特性[21]。凌同华等[22-24]对应力波信号进行了小波包变换，以应力波不同频率的频带能量占比为出发点，探究了不同工况下的频率及频带能量的分布特征，从频域的角度分析了应力波传播的衰减特性。已有对波的频谱分析和频带能量的研究主要围绕工程实际中的爆破冲击波，而关于特定地应力中的应力波频散特性的研究较少。本研究通过室内试验建立特定静应力环境下的应力波传播模型，探究应力波的衰减特性并建立梯度应力下岩石应力波频散的经验模型，对于工程实际评估围岩(体)的稳定性具有重要的理论指导意义。

本文作者旨在研究不同应力梯度对岩石应力波传播衰减规律及频散特性。利用自主研制的具有梯度静应力岩石应力波传播试验系统，进行具有不同静应力梯度工况的应力波传播试验，得到应力波的时域波形曲线。通过快速傅里叶变换和小波包分解与重构，将梯度静应力环境下的应力波分解为不同频率下的谐波分量，从应力波传播和频散的角度，表征梯度应力环境下岩石应力波的传播衰减特性，分析梯度应力环境下的应力波频谱幅值、质心频率、频谱峰值、频带能量的变化规律，构建梯度应力环境中质心频率和应力波总能量随空间衰减的经验模型。本文的研究结果有助于完善应力波传播理论。在地下实际工程岩体爆破过程中，峰值与频率特性对构筑物的破坏或稳定性有重大影响。

1 试验

1.1 试件制备

选用均质性良好、内部无明显缺陷的赣州红砂岩制备岩石试件。红砂岩密度为2 388 kg/m3，纵波波速为2 414 m/s。由于本试验旨在研究梯度应力岩石的应力波传播特性，故将红砂岩研磨加工为长方体试件，其长度×宽度×高度为1 500 mm×100 mm×60 mm。为防止试件受轴压时发生失稳，其横截面不平行度与不垂直度误差为0.02 mm。

试验所用红砂岩的单轴压缩应力-应变曲线如图1所示。由图1可知：随着轴向应力的增加，试件的变形会经历孔隙压密—弹性变形—损伤演化—失效破环4个主要阶段。这说明当岩石长试件受静应力梯度加载时，由于不同位置的轴向应力不同，导致不同位置的变形程度不同，进而导致岩石在轴向上的物理特性不同。

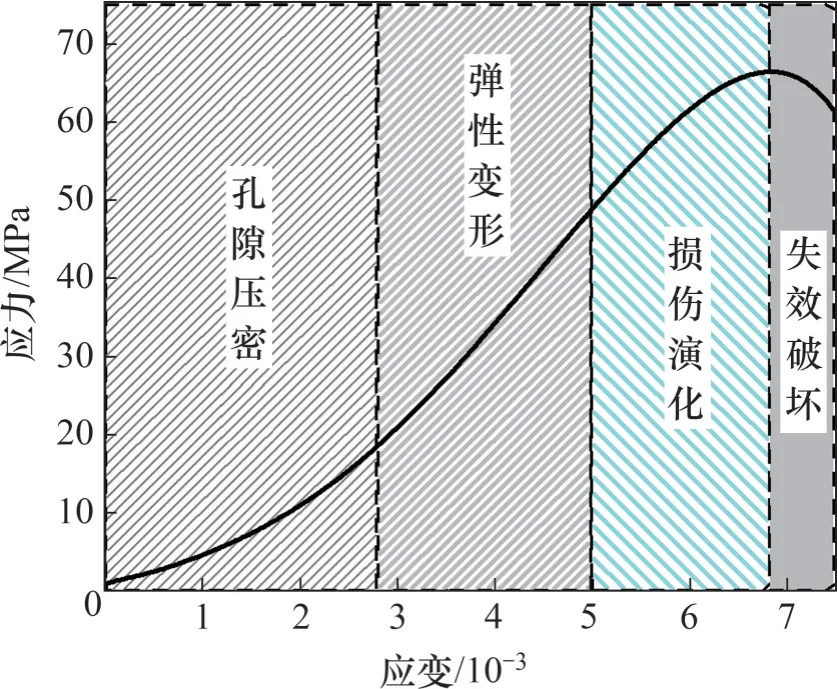
图1 红砂岩的单轴压缩应力-应变曲线Fig.1 Stress-strain curve of red sandstone under uniaxial compression

试件尺寸及应变片布置示意图如图2所示。为最大限度地消除试件偏心压缩对应力波的影响，将应变片对称地粘贴在试件前后两侧面的轴线上，从右至左依次分布测点A、测点B、测点C、测点D和测点E共5 个测点，如图2 所示。测点A距离入射端间距为200 mm，大于横截面的最大尺寸。消除了端部不均匀压缩的影响。同时为了避免采集的应力波夹杂透射端的反射波信号，测点E距离透射端为700 mm，相邻测点的间距为150 mm。

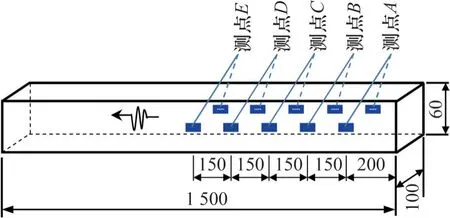
图2 试件尺寸及应变片布置示意图Fig.2 Specimen size and strain gauge arrangement

1.2 试验系统

试验采用自主研制的具有梯度静应力的岩石应力波传播试验系统，该试验系统由动力装置、梯度静应力加载装置及数据采集单元组成，如图3所示。动力装置主要由高压氮气瓶、高压气室、纺锤形冲头、发射腔组成。数据采集单元主要由CS-ID 超动态应变仪、DL-750 示波器和计算机组成。

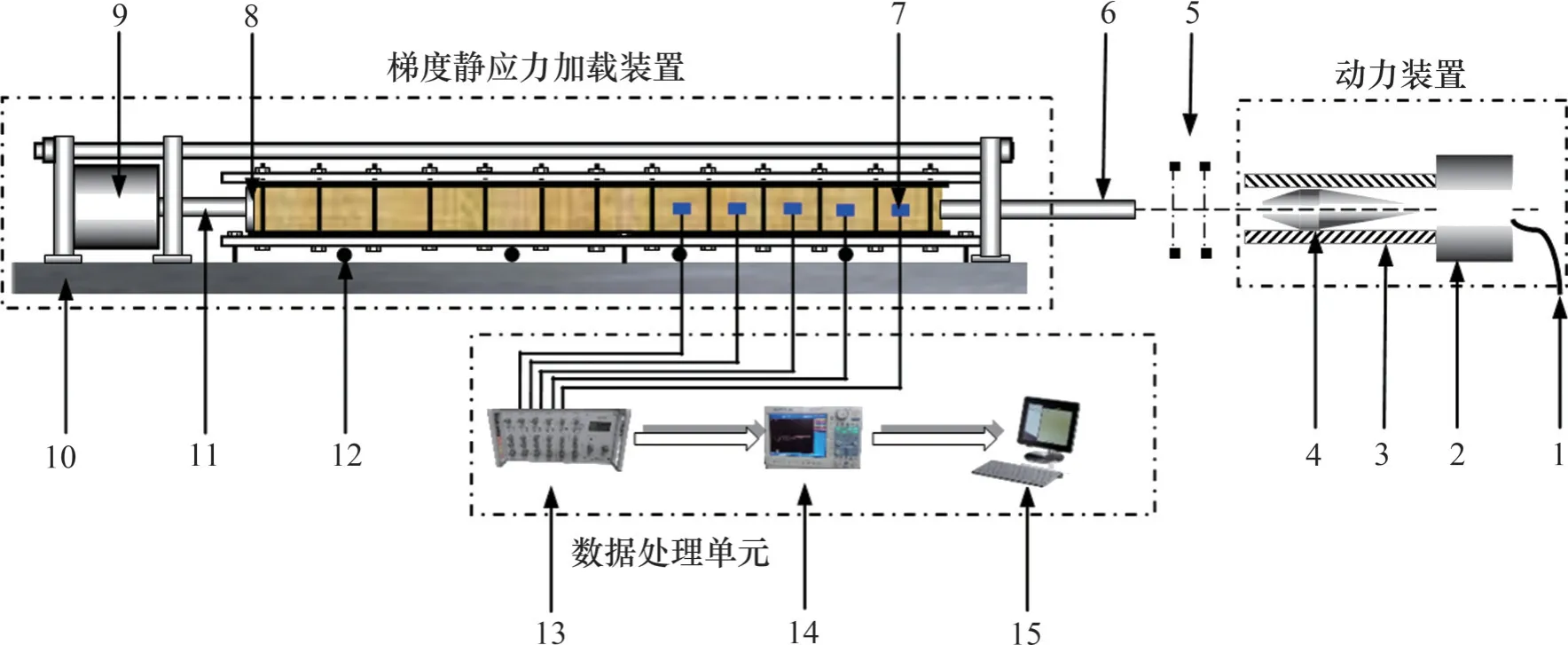
图3 具有梯度应力的岩石应力波传播试验系统Fig.3 Test system for stress wave propagation in rocks with gradient stress

梯度静应力加载装置置于霍普金逊杆的基座平台和支架上，装置的组成部分从左至右依次是轴压加载单元、轴压加载杆、保证试件端面均匀加载的钢垫片，以及梯度静应力主要装置部分。其中，梯度静应力主要装置部分及线性梯度静应力实现原理如图4所示。装置构成从上到下依次为带橡胶垫的上层钢板、岩石试件、带橡胶垫的下层钢板，上下层钢板通过预留螺栓孔用螺栓连接。图4中的轴向荷载F由轴向加载单元提供，法向均布荷载FN(x)由螺栓提供，作用于钢板上的支持力F/2由支架提供。

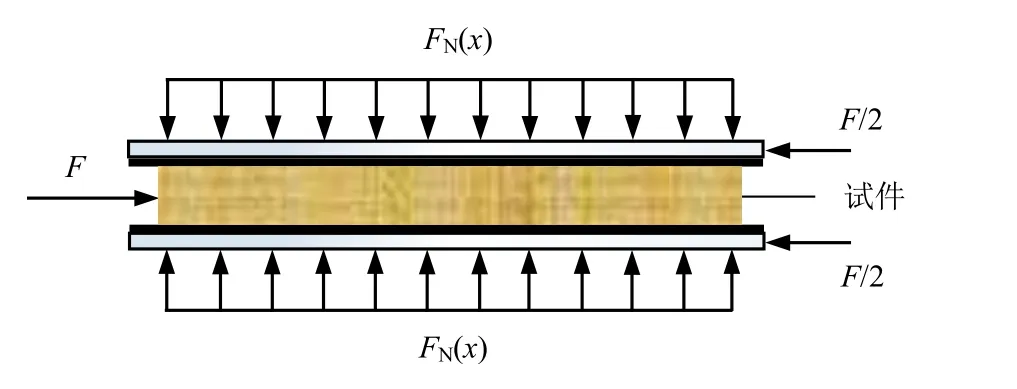
图4 线性梯度应力实现原理示意图Fig.4 Schematic diagram of principle of linear gradient stress implementation

据图4分析试件的受力情况。当试件处于临界平衡状态时，轴向荷载F与试件上下侧面静摩擦力满足关系式：

式中：Ff(x)为作用在试件上下侧面单位长度摩擦力，kN/m；l为试件长度，m。

由静摩擦库仑定律可得

式中：FN(x)为作用在试件上下侧面单位长度法向压力，kN/m；fs为试件与接触物体的静摩擦因数。

当法向荷载FN(x)为均布载荷时，Ff(x)沿试件的长度方向为定值Ff，式(1)变为

此时，图2 中距右侧端面为x的横截面上的轴向静应力为

式中：A为试件的横截面面积。

由式(4)可知，2Ff/A为静应力的梯度。由于单位长度摩擦力与单位长度法向荷载FN(x)成正比，试验中可以通过改变单位长度法向荷载FN(x)，得到不同的静应力梯度[4]。

1.3 试验方法

在冲击加载前，先利用梯度静应力加载试验装置对岩石试件施加梯度静应力，本试验分别设置6 种静应力梯度(k)工况：0、6.87、10.39、16.66、20.19和22.57 MPa/m。

每一种静应力梯度工况施加完成后，利用高压氮气驱动异形冲头撞击入射杆，在撞击的瞬间将产生应力波，应力波最终会在具有梯度应力的岩石长试件中传播，应力波信号被应变片捕捉，经过数据处理单元，得到不同梯度应力工况下不同测点处的应力波时域数据。

在所有静应力工况的应力波传播试验中，均用近似相同的冲击速度冲击入射杆产生应力波，具体的冲击速度如表1所示。表1中加载参数是旋紧力矩和油压表读数，二者依次对应于法向荷载与轴向荷载，由式(1)～(4)计算可得到应力梯度。

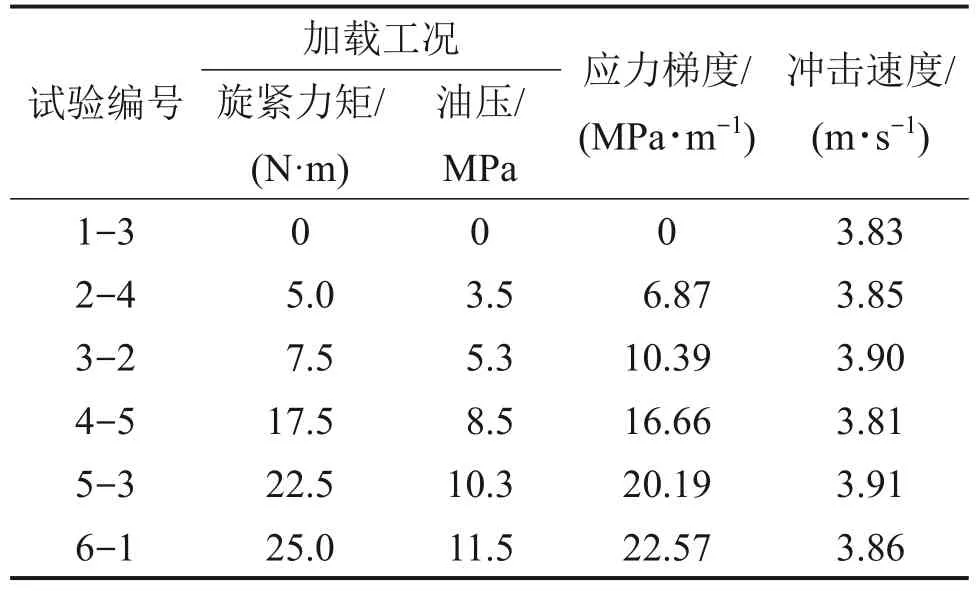
表1 不同应力梯度工况时的动静组合加载数据Table 1 Combined dynamic and static loading test data at different stress gradient working conditions

2 试验结果

在6 种静应力梯度工况下，在A、B、C、D、E这5个测点采集的应力波时域波形如图5所示。

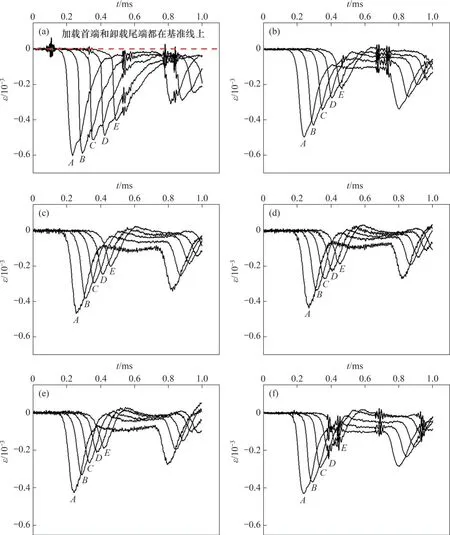
图5 不同静应力梯度下的应力波时域波形Fig.5 Time domain waveform under different stress gradients

由图5可以看出：在同一应力梯度下，随着传播距离的变化，应力波形状变化不大；随着应力梯度增加，应力波时域波形也基本一致。但在梯度应力的作用下，岩石中的应力波的卸载段尾部应力波曲线不能恢复到基准线水平。造成这一现象的原因是，在应力波卸载阶段，试件压缩后的变形恢复，对岩石进行梯度应力加载后，法向荷载和轴向荷载同时约束了试件恢复变形的能力，导致其不能恢复到初始应变。

在频域内，可将任意形式的应力波分解为不同频率的谐波分量。由于不同频率的谐波分量其波数、衰减系数有所不同，故应力波在岩石中传播时，其波形将发生改变[25]。本文采用快速傅里叶变换和小波包分解与重构，将梯度静应力环境下的应力波分解为不同频率下的谐波分量，通过应力波频谱特性和频带能量来表征梯度应力下岩石中应力波的衰减特性。

3 梯度静应力对频谱特性的影响

针对图5所示的应力波时域数据，绘制典型波形，如图6 所示(其中，ε0为应力波初始应变，εmax为完整半正弦应力波最大应变，εmin为完整半正弦应力波最小应变，εp为平台应变，t1为应力波起跳对应时间，t2为完整半正弦应力波最大应变对应时间，t3为完整半正弦应力波最小应变对应时间)。图6中，t1-t3时段是动荷载的一个完整的加卸载过程，故选取t1-t3时段的应力波时域数据进行快速傅里叶变换(FFT)。

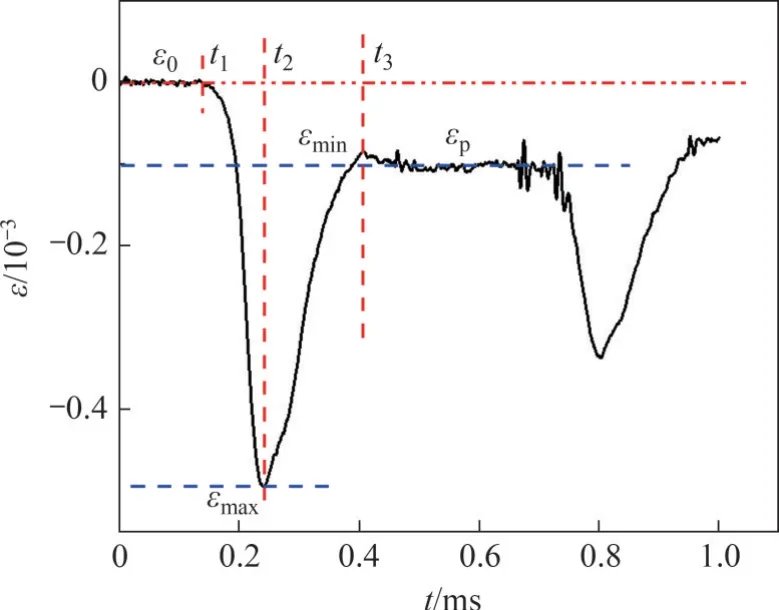
图6 典型应力波波形Fig.6 Typical stress wave shape of red sandstone

在不同应力梯度下，岩石中应力波时域数据经快速傅里叶变换后的频谱图如图7所示。当频率大于20 kHz时，幅值趋于零，故图7只画出频率在0～20 kHz之间应变ε幅值的变化曲线。岩石中的应力波信号能量主要集中在低频段且频带较宽，这与实际岩体爆破工程中所采集到的振动信号相同[26]。

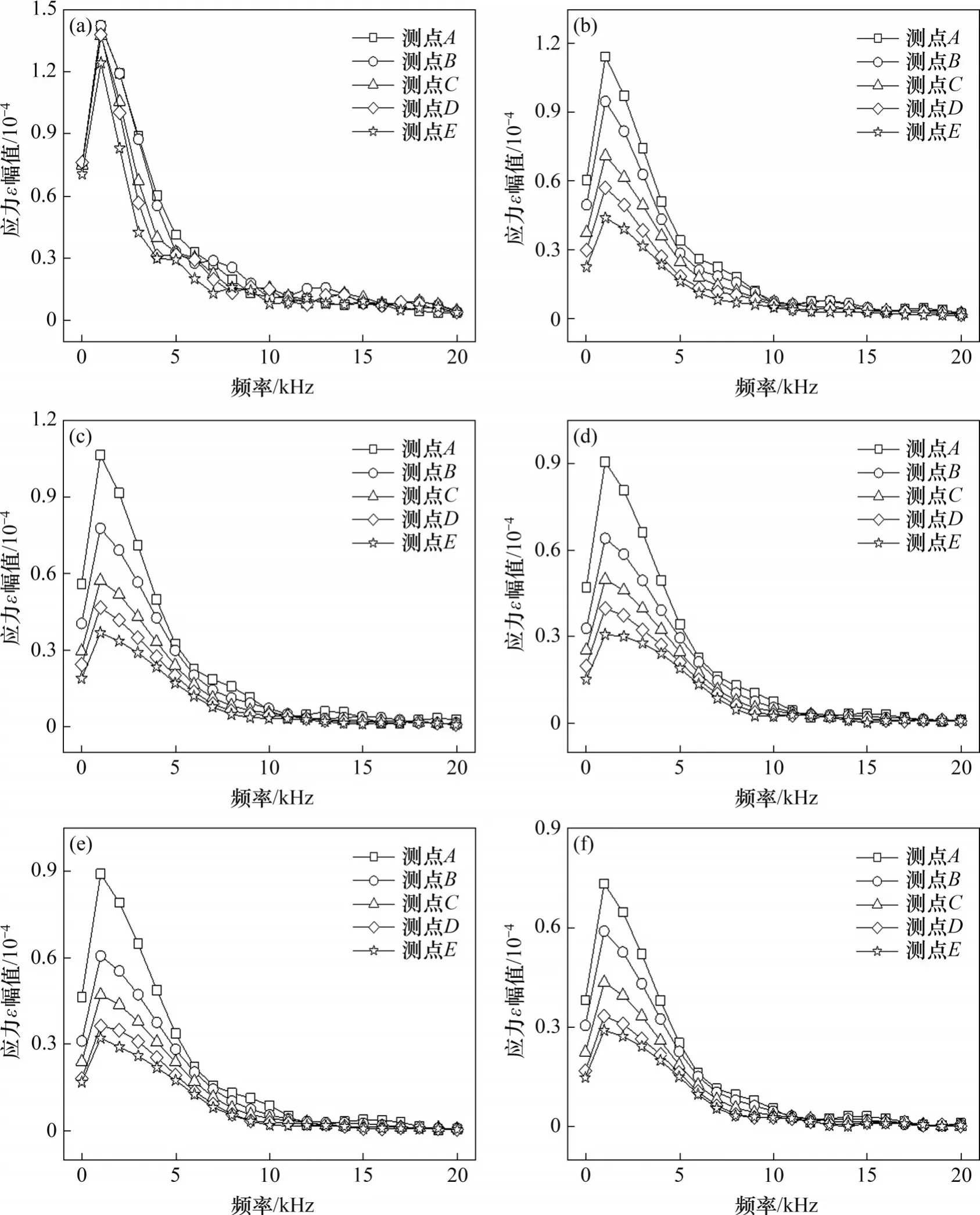
图7 不同应力梯度下的各测点频谱图Fig.7 Spectrum amplitudes of each measuring point under different stress gradients

由图7可以看出：所有工况不同位置处的波分量幅值主要集中在频域0～7.5 kHz 内；在频带0～7.5 kHz 之内，无梯度应力时的频谱幅值随传播距离基本不变，但有梯度应力作用时，频谱幅值随传播距离的增加越来越低，这表明应力梯度对低频信号有较大影响。无梯度应力时的频谱整体高于有梯度应力作用时的频谱，并且随着应力梯度的增加，频谱幅值整体呈下降趋势；在同一梯度应力下，随着传播距离增加，频谱幅值也呈下降趋势。

3.1 质心频率随传播距离的变化

为进一步分析梯度应力下岩石中应力波频谱的偏移情况，本文引入质心主频来反映频散特性。质心频率fc是频谱幅值曲线与坐标轴所围成图形的形心对应的频率。由图7所示的频谱幅值图计算不同工况下0～7.5 kHz 范围内的质心频率fc，得到不同工况下质心频率随传播距离的变化关系，如图8所示。

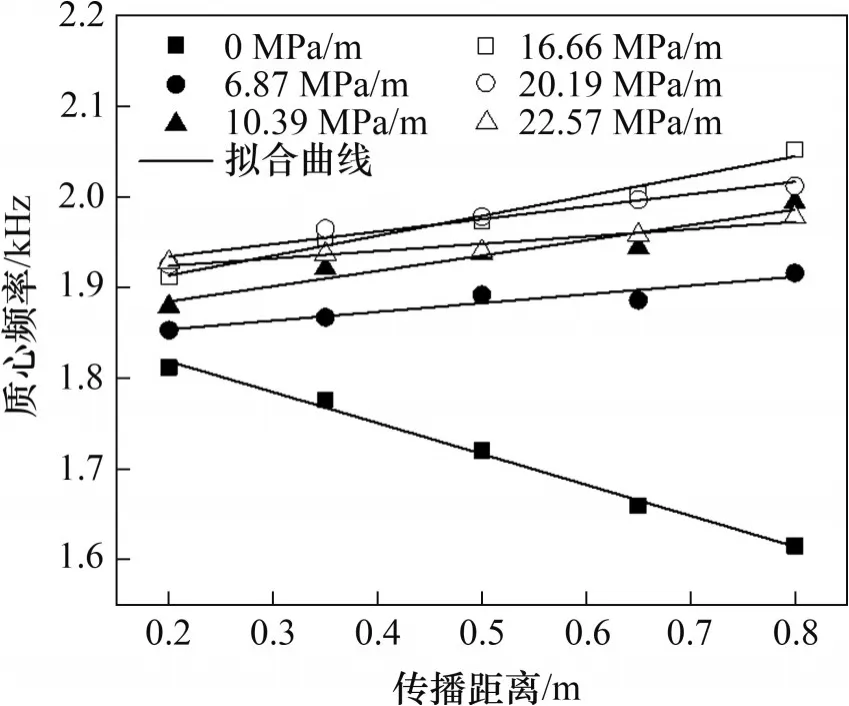
图8 质心频率随传播距离的变化Fig.8 Centroid frequency varies with propagation distance

由图8可知：在无梯度应力作用时，质心频率随着传播距离的增加呈减小趋势。而在梯度应力作用下，岩石质心频率随着传播距离的增加呈增大趋势。经分析可知，主频升高对应岩石孔隙的闭合，主频降低对应岩石微裂隙的形成[27-28]。当无梯度应力作用时，岩石内部的孔隙自然分布，应力波的各谐波分量在岩石中传播衰减，符合低频传递、高频衰减的理论[26]，故应力波质心频率呈减小趋势；而应力波在具有梯度应力的岩石中传播时，由于岩石所受到的轴向应力是呈梯度的，从近端至远端岩石越密实，故应力波质心频率向高频发展。

将图8 中的质心频率与传播距离进行函数拟合，拟合函数及相关系数R2如表2所示。由图8和表2 可知：拟合函数相关系数R2均大于0.9，拟合程度良好，表明岩石应力波质心频率与传播距离呈现良好的线性关系。

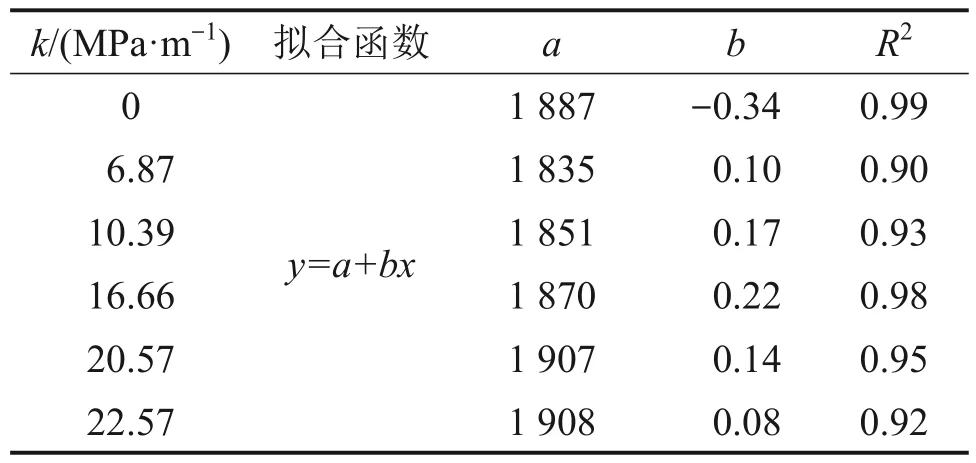
表2 应力波质心频率与传播距离间的拟合关系结果Table 2 Fitting results between centroid frequency and propagation distance

3.2 质心频率随应力梯度的变化

质心频率随应力梯度的变化如图9所示。由图9可以看出：所有测点的应力波质心频率随应力梯度的增加具有相同的变化趋势；随着应力梯度增加，岩石中应力波的质心频率呈现先增加后平稳或出现减小的趋势，究其原因，岩石孔隙闭合总是对应于应力波质心频率的升高，而岩石微裂隙的产生促使质心频率降低；当岩石受到轴向静应力时，岩石中孔隙逐渐被压密的同时伴随着少数裂隙的萌生。岩石低轴向静应力阶段，以初始孔隙压密为主，质心频率向高频发展；随着应力梯度的增加，岩石内部孔隙被压实，使微裂隙增生，故质心频率呈减小趋势。

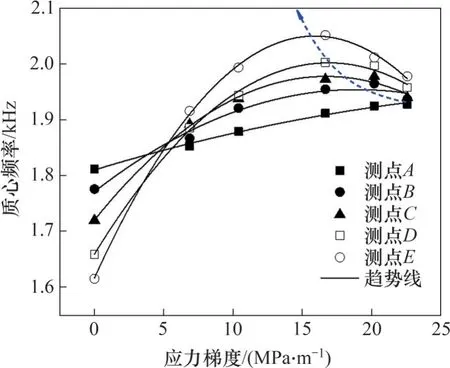
图9 质心频率随应力梯度的变化Fig.9 Centroid frequency varies with stress gradient

由图9还可以看出：随着应力波传播距离的增加，质心频率先增加后减小的转折点对应的应力梯度越来越小。经进一步计算可得，转折位置对应的轴向应力在10～12 MPa之间。

3.3 应力波频谱峰值

图7所示的频谱幅值图中，在所用工况下，所有测点都具有单峰值，其对岩石应力波的衰减起主导作用，将频谱幅值的峰值(下文均称频谱峰值εf,max)作为因变量，具体分析不同工况下频谱峰值的变化规律。

图10 所示为频谱峰值的变化规律。由10(a)可知：在无梯度应力作用下，频谱峰值随着传播距离的增加缓慢衰减；在梯度应力作用下，频谱峰值先快速减小，再缓慢减小。经分析可知，当无梯度应力作用时，岩石中应力波的频谱峰值主要受岩石孔隙度的影响，故其频谱峰值自然衰减；当有梯度应力作用时，在应力波传播方向的近端到远端，岩石中的轴向应力会增加，所以，在轴向方向上，岩石依次经历了初始孔隙压密-孔隙完全压密阶段，进而形成了梯度的波阻抗，由于应力波在传播至波阻抗改变的截面时会发生反射，从而影响应力波的衰减特性[29]，故造成频谱峰值呈快速减小的趋势。当轴向应力增加到一定程度时，岩石内部孔隙被完全压密，随着应力梯度的增加，振动阻力变化不大，从而，频谱峰值变化较小且所有工况频谱峰值趋于同一个值。

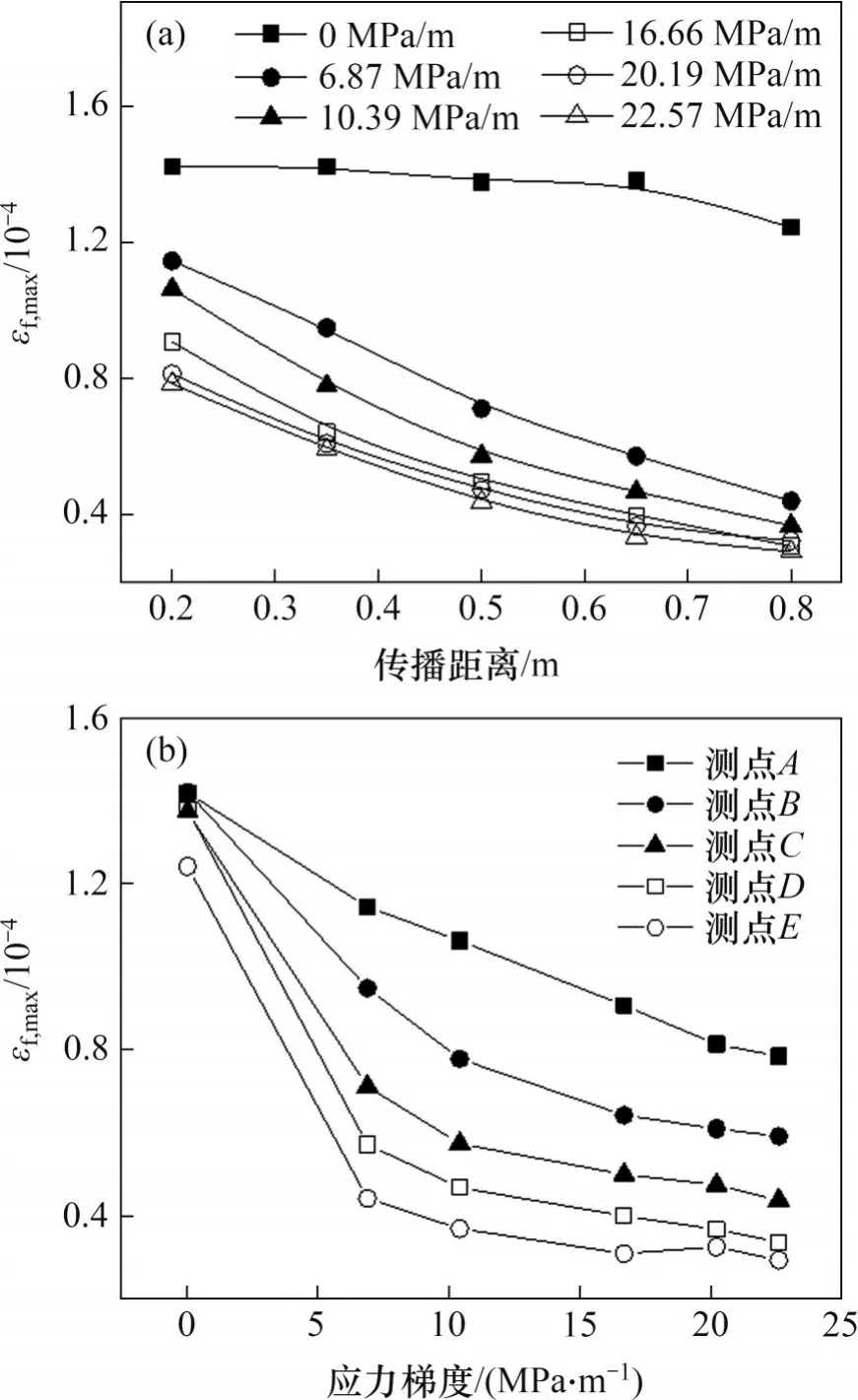
图10 频谱峰值εf, max的变化规律Fig.10 Change of spectrum peak εf, max

由图10(b)可知：随着应力梯度增加，频谱峰值均降低，其中测点A处的频谱峰值呈“快速降低”的变化趋势测点，测点B、C、D、E的频谱峰值呈“快速下降—平稳发展”的变化趋势。

4 梯度静应力下岩石的频带能量

4.1 小波包变换

为进一步研究梯度应力对应力波频散特性的影响，基于小波分析理论，对应力波信号进行小波包分解，得到梯度应力下应力波总能量的衰减特性和应力波的频带能量的分布特征。

本试验设置的采样频率为1 MHz，根据采样定理，其奈奎斯特(Nyquist)频率为500 kHz。将应力波信号分解为12 层，将其第m层分解共得到2m个小波包，共计4 096个小波包，每一个小波包对应一个频带，频带带宽为122.07 Hz。结合小波包求解频带能量的公式，第12 层各个节点信号的能量可定义为

式中：xj,k为重构信号S12,j的离散点的幅值；j=0，1，2，…，212-1；k=0，1，2，…，m；m为试验中采集到的数据点数。

将第12 层分解得到的所有重构信号对应的能量E12,j相加即为原始应力波信号的总能量E0：

则各个频带能量占总能量的比例为

式中：Q12,j为能量占比。

通过频带能量公式在MATLAB 中编写小波包计算程序，对不同工况下的应力波时域信号经小波包分解重构后，即可同时得出梯度应力下应力波总能量的衰减规律以及频带能量的分布情况。

4.2 梯度应力作用下应力波总能量的衰减

由小波包分解程序得到不同应力梯度下各个测点处应力波信号频带总能量E0。应力波信号总能量与传播距离的变化关系如图11所示。

图11 红砂岩应力波总能量随传播距离的变化关系Fig.11 Variation of total stress wave energy with propagation distance in red sandstone

由图11 可以看出：在无梯度应力作用下，应力波总能量随传播增加呈现“逐渐减小”的趋势；而在梯度应力作用下，应力波总能量随传播增加呈现“快速减小—平稳发展”、与无梯度应力作用不同的趋势。表明岩石应力波在传播过程中，总能量会发生衰减，但梯度应力对岩石应力波总能量的衰减规律影响较大。

为了得到应力波总能量与传播距离之间的经验模型，对应力波总能量和传播距离的关系进行拟合，拟合关系如下：

式中：α为与应力梯度有关的参数；β为与岩石孔隙度有关的参数。

对图11 中的岩石中应力波总能量与传播距离进行函数拟合，拟合函数及相关系数如表3 所示。由图11 和表3 可知：拟合函数相关系数R2均大于0.97，拟合程度较高，表明岩石应力波总能量与传播距离在无梯度静应力状态下呈现较好的线性关系[24]；而在梯度应力下，应力波总能量与传播距离的幂函数呈现较好线性函数关系。这进一步说明，此经验模型可以较好地表征梯度应力下岩石应力波总能量与传播距离的关系，可为预测爆破开挖时地下工程岩体的应力波传播衰减提供参考。

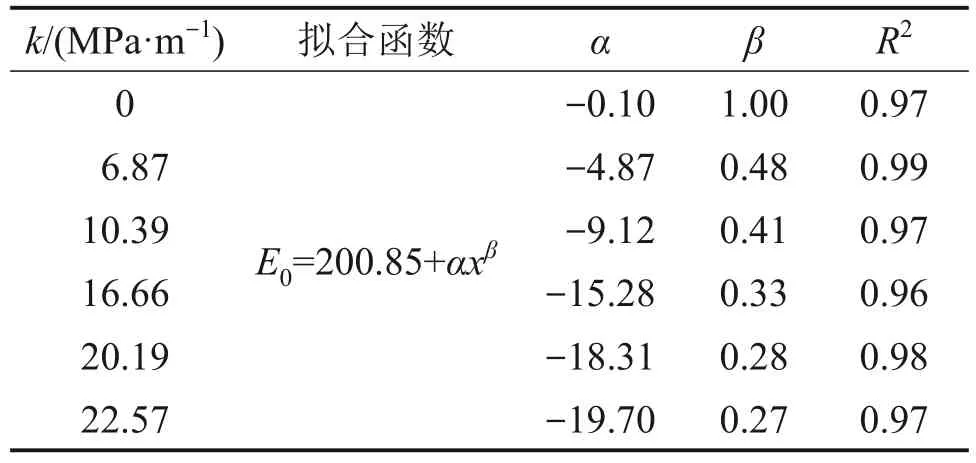
表3 应力波总能量与传播距离间的拟合结果Table 3 Fitting results between total stress wave energy and propagation distance

由表3可以看出：随着应力梯度的增加，拟合参数α和拟合参数β都呈减小趋势。为了考察更多工况下岩石应力波总能量与应力梯度和传播距离之间的关系，对6个应力梯度下的α和β进行拟合，α和β与应力梯度的关系如图12所示。

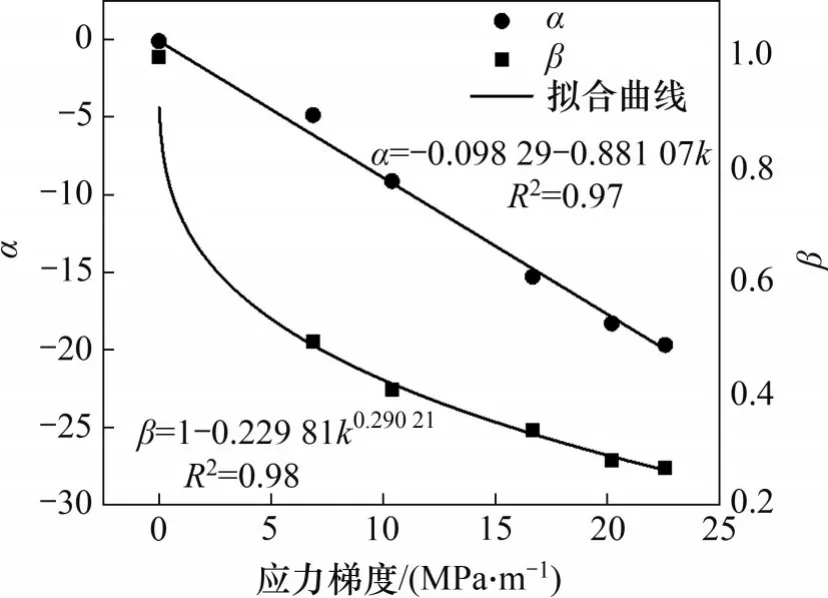
图12 α和β与应力梯度的关系Fig.12 Relationship between stress gradient and α, β

由图12 可知：拟合参数α随着应力梯度的增加呈线性减小，这是与应力梯度直接相关的物理参数；拟合参数β随着应力梯度的增加先减小后平稳发展，经分析可知β与岩石空隙度有关，可定义为与岩石波阻抗有关的物理参数。2个拟合关系式的相关系数分别为0.97和0.98，拟合程度较高。利用拟合关系式(4)以及图12 进行计算，可以得到任意应力梯度工况下应力波总能量随传播距离的衰减关系曲线，如图13所示。

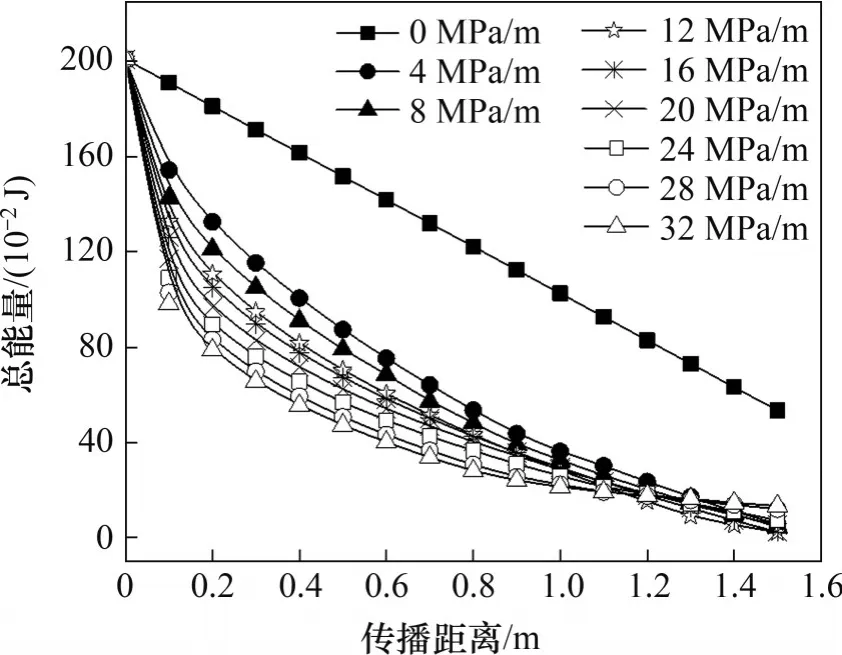
图13 红砂岩应力波总能量随传播距离的变化规律Fig.13 Variation rules of total stress wave energy with propagation distance in red sandstone

由图13 可知：应力波总能量在均质的岩石中传播衰减受到孔隙度的影响，此时，岩石中应力波总能量呈线性衰减；岩石在梯度应力环境下，应力波总能量的变化经历先快速衰减再缓慢衰减的阶段，其中，应力波总能量在快速衰减阶段的衰减速率比自然状态下的衰减速率更快，表明岩石应力波总能量的衰减受梯度应力的影响较大，这是因为应力波总能量的衰减同时受到孔隙程度和应力梯度的控制。

经进一步分析可知，在梯度应力作用下的岩石会形成梯度的波阻抗，在波阻抗发生变化的截面，应力波的反射和透射特性会发生改变。分析梯度应力作用下岩石的轴向应变时，波阻抗梯度由大变小，导致在梯度应力作用下岩石应力波总能量衰减更快。同时，由图13 还可看出，在高静应力梯度作用下，应力波总能量在缓慢衰减阶段越平缓，这是因为此时岩石已趋于弹性阶段，波阻抗梯度和孔隙度随传播距离的变化都很小，故能量的衰减较小，总能量逐渐趋于平稳。

4.3 频带能量的分布

为分析应力波信号频带能量分布特征，得出不同测点不同应力梯度下的频带能量占比情况。将12层4 096 个小波包重构成8 个频带，分别为[0，3.91)、[3.91，7.81)、[7.81，15.63)、[15.63，31.25)、[31.25，62.50)、[62.50，125.00)、[125.00，250.00)、[250.00，500.00] kHz，各频带对应频带相对能量占比见表4。

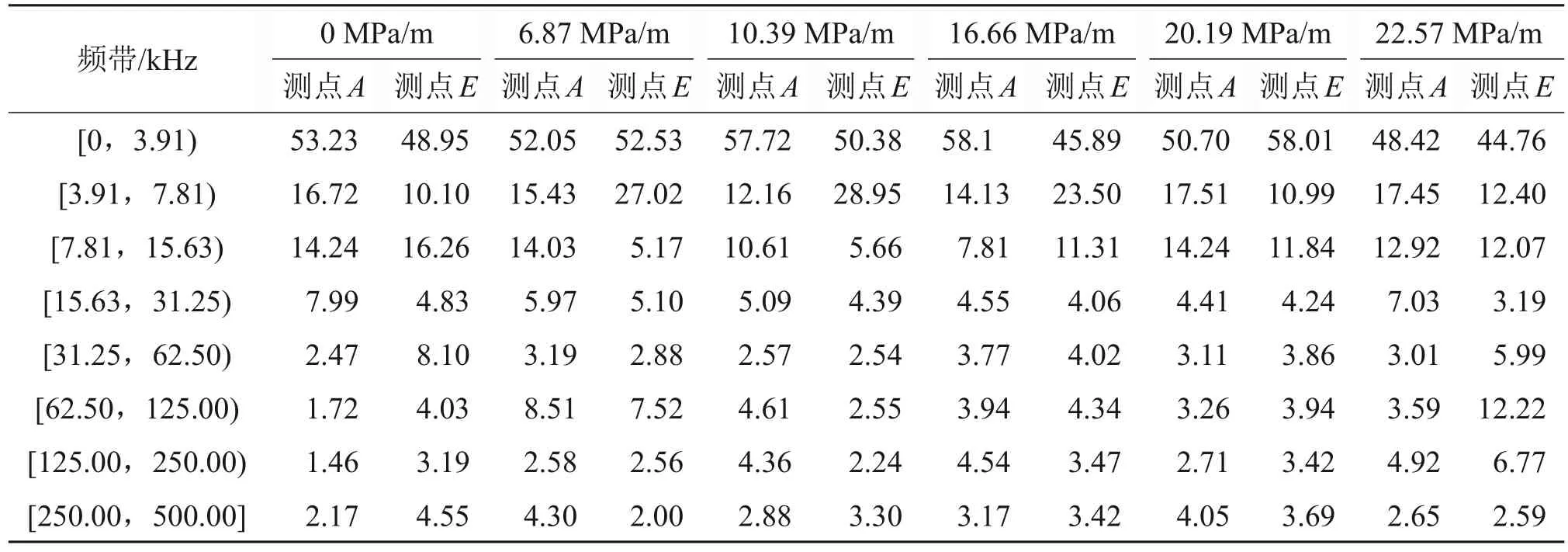
表4 不同应力梯度下测点A和测点E频带能量占比Table 4 Frequency band energy ratio at point A and E under different stress gradients %

由表4 可知：虽然频带[0，3.91) kHz 和[3.91，7.81) kHz 的频带宽度相对较小，但其所占频带能量较多，其中，频带[0，3.91) kHz 占总能量的一半左右，无论有无梯度应力的作用，能量主要分布于0～7.81 kHz，这部分能量占频带总能量的80%左右；后几个频带较宽，但其所占能量较少。以上结果表明，应力波信号的成分以低频为主，高频成分所占比例极少。

为进一步分析应力波频带相对能量随传播距离的变化情况，在所有工况下，频带能量占比的变化主要集中于0～7.81 kHz，测点A与测点E的前2个频带的小波包能量占比如图14所示。

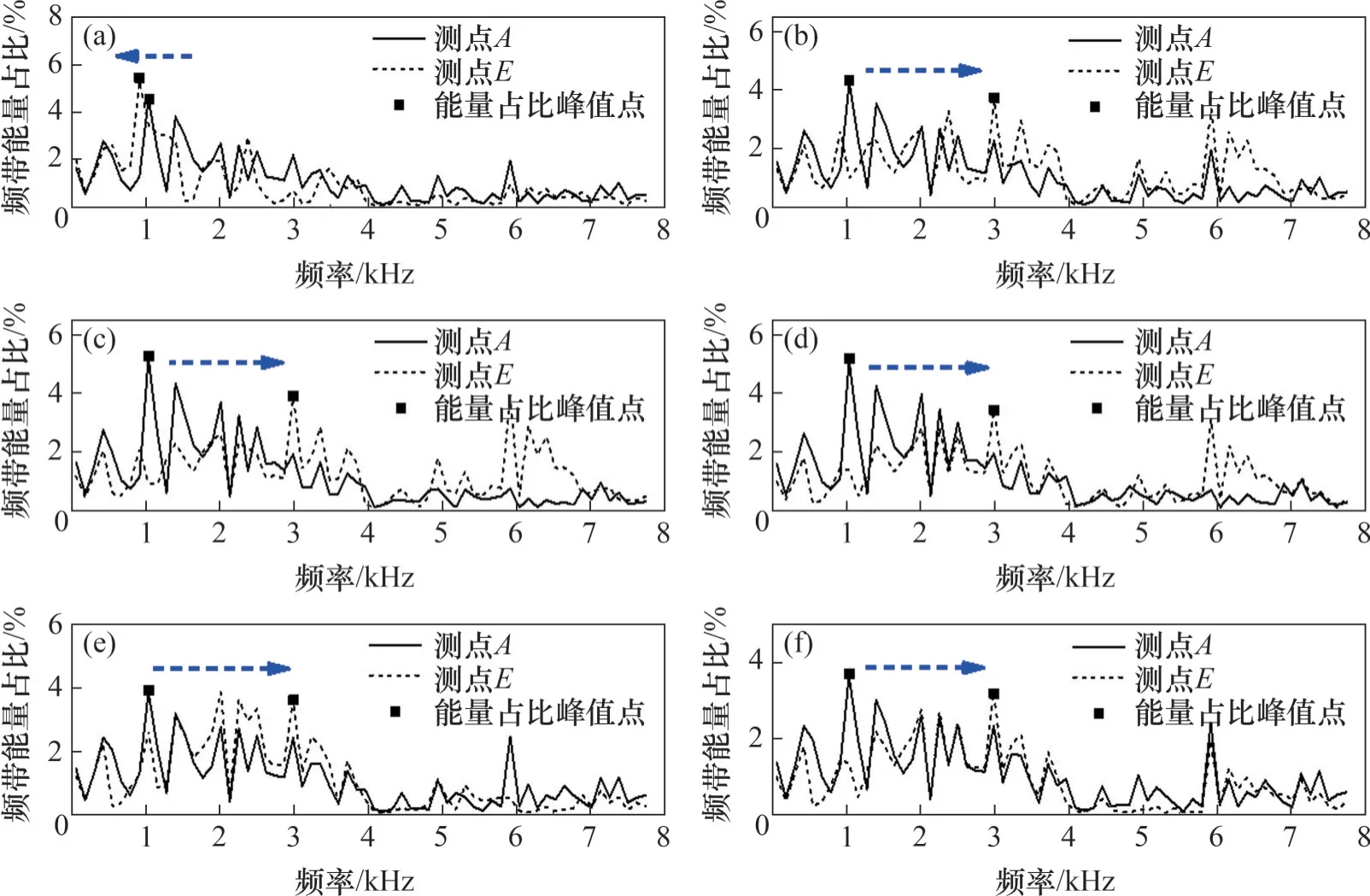
图14 频带0～7.81 kHz的频带能量占比Fig.14 Frequency band energy ratio of 0-7.81 kHz

由图14 可以看出：在无梯度应力作用时，随着传播距离的增加，相对频带能量有往低频偏移的趋势；岩石在梯度应力作用下，随着传播距离增加，相对频带能量有往高频偏移的趋势。而此时在前2 个频带(0～7.81 kHz)的能量对整体频带能量的变化起决定性作用，故在整个频带(0～500 kHz)能量的偏移与图14 中的偏移情况一致。在无梯度应力作用时，频带能量随传播距离的增加往低频偏移，即质心频率减小；在梯度应力作用时，频带能量随传播距离的增加往高频偏移，即质心频率增加。当梯度增加到一定程度时，质心频率的变化较小。这与质心频率随传播距离的变化情况一致，这进一步验证了质心频率的变化规律。

5 结论

1) 无论岩石是否受到梯度应力作用，各个测点频谱曲线均成抛物状。通过岩石的应力波频谱幅值主要集中于低频带(0～7.81 kHz)，梯度应力对低频带的影响较大。

2) 岩石中应力波的质心频率随空间距离的频散特性中，在无梯度应力作用时，质心频率随传播距离的增加而呈线性减小；在有梯度应力作用时，质心频率随传播距离的增加呈线性增加。在质心频率随应力梯度的变化特性中，对于同一测点，应力波信号质心频率随应力梯度的增加呈先增加后减小的趋势。质心频率的变化受不同频率谐波信号的衰减量的影响，本质上由岩石内部孔隙的变化决定。

3) 在无梯度静应力作用时，频谱峰值随着传播距离的增加缓慢衰减；在有梯度应力作用时，频谱峰值先快速减小，再缓慢变化，其同时受到孔隙度和梯度波阻抗的影响。频谱峰值随着应力梯度的增加，呈先迅速降低再平稳发展的趋势。频谱峰值迅速降低阶段主要表现在从梯度应力的无到有的过程，在本质上是岩石内部被压密而形成的约束从无到有的过程，导致频谱峰值迅速降低。

4) 岩石应力波总能量与传播距离在自然状态下呈现较好的线性关系，而在梯度应力下，应力波总能量与传播距离的幂函数呈现较好线性函数关系。由此可知应力波总能量的衰减同时受孔隙度和梯度波阻抗的控制。

5) 应力波信号能量主要集中在低频带(0～7.81 kHz)内。在任何工况下，在0～3.91 kHz 频带内，能量占总能量的一半左右。对比分析不同测点处频带能量随着应力梯度的变化情况，发现频带能量在梯度应力作用和无梯度应力作用下频带能量的偏移情况不一致。