夹竹桃根系拉拔力学试验及计算模型研究

杨果林，李亚龙，林宇亮，李琪焕，李海峰

(中南大学 土木工程学院，湖南 长沙，410075)

膨胀土是一种具有典型的吸水膨胀、失水收缩特点的特殊土体，导致膨胀土边坡滑动破坏十分频繁，造成巨大的经济损失。林宇亮等[1-3]从失稳机理、结构防护以及土体改良等方面提出了解决方法。植物防护是利用根系固土原理稳定岩土边坡同时美化生态环境的一种新技术，该技术不同于传统的膨胀土处治方式，具有成本低、易施工、保护生态环境等优点，最重要的是植物根系能提高膨胀土边坡的稳定性。根系发挥稳固边坡土体的作用主要来自两方面：一是通过形成根土复合体，增强边坡整体性；二是植物叶片可以防止雨水直接落向边坡，降低边坡土体冲刷量。目前，绝大多数的植物根系固土护坡方案以绿化环境和美化视觉为目的，并没有达到提高边坡稳定性的效果，而且在实际工程中，很多植被护坡方案缺乏系统的理论作指导，难以对植被防护边坡稳定性进行评估，极大限制了该技术的应用。现有研究结果表明，根系抗拉力与根径呈幂指数关系，与根系数量呈线性关系，与株高呈指数关系[4-5]。在相同土体干密度条件下，根系的最大拉拔力随龄期的增加呈现出增大的趋势。在根系拉拔试验中，单一根系在土体中的破坏模式分为拔出破坏和拉断破坏[6]，拔出破坏是由根系在土体中滑移造成的，拉断破坏是由根系在土体中断裂造成的。基于根系的拉断破坏模式，WU等[7]基于摩尔-库仑理论建立了计算植物根系对土体抗剪强度影响的理论模型—WU 模型，由于该模型参数简单、适用性强被广泛用于评估不同类型植物的固土作用。然而，该模型假设所有根系在达到最大抗拉强度瞬间同时被断裂，因而，模型显著高估了根系对土体抗剪强度的贡献。后续研究从不同的切入点建立了新的理论模型，如考虑根系动态断裂的纤维束模型[8]、基于根系拉伸力-位移关系的纤维增强模型[9]、基于土体剪切位移的强度模型[10]。虽然这些模型对根土相互作用机理进行了深入研究，但缺乏对根土界面摩阻特性的分析，且由于模型参数复杂，因此，较少在工程实践中得到应用。此外，即使是目前常用的WU模型，对其的修正研究主要集中在探究不同植物类型的修正系数[11-12]以及考虑根系的变形对模型参数的影响上[13-14]，并未充分考虑根土界面间的摩阻作用。然而，根土界面间的摩阻作用是根系发挥加固土体作用的前提条件[15]。根系通过根土界面的摩阻作用嵌固在土体中，使得根土复合体形成一个共同受力整体抵抗外荷载[16]。综上所述，大部分研究均只考虑根系断裂时抗拉力，而忽略了摩阻作用而产生的抗拔力，导致计算出的理论拉拔力与根系实际拉拔力存在较大区别。为此，本文以不同龄期夹竹桃根系为研究对象，基于根系拉断破坏和拔出破坏这2种模式，提出根系整株拉拔力学模型，将计算结果与实测结果进行对比，验证模型的合理性，以便为根系抗拔力学效应的定量评价提供依据。

1 试验

1.1 试验材料

本次研究的试验区位于湖南省长沙市跳马镇，属于长江上中游地区，气候为亚热带季风气候，年均降雨量为1 361.6 mm，年均气温为16.8～17.2 ℃，气候适宜，土体肥沃，植被覆盖率高。根据长江上中游地区的气候条件，结合铁总建设[2013]94号《铁路工程绿色通道建设指南》[17]，选取常见灌木植物夹竹桃作为试验对象。夹竹桃具有喜光、喜温暖湿润、不耐寒等特性，适生于排水良好、肥沃的中性土壤，是一种铁路边坡大量采用的优良护坡植物。试验区的土体为红壤，属于粉质黏土，土体参数如下：重度为1.46 g/cm3，含水率为16.8%，土粒相对密度为2.73。

夹竹桃根系发达，毛细根多，平均根深60 cm，根系的韧性较强。为对比生长龄期对根系固土效果的影响，试验选取龄期为1、2、3 a的夹竹桃进行整株原位拉拔试验，测定其最大拉拔力，同时，以整株挖掘法获取各龄期代表性植株进行形态学指标统计及拉伸试验。原位拉拔试验进行9次，所有植物均一次性拔出，同时，采用整株挖掘法获得植株3株。现场试验完成后，称取植株质量并放入保鲜袋带回实验室。原位拉拔试验获取的整株夹竹桃如图1所示，其龄期从左至右分别为3 a、2 a和1 a。

图1 不同龄期夹竹桃形态Fig.1 Morphologies of oleander at different ages

1.2 试验方法

1.2.1 夹竹桃标准株选取

首先将3个龄期的研究区均划分为左、中、右3个区域，然后在每个区域内随机选取长势良好的植株3株，测量其株高和地径并计算出平均值，最后在该区域内挑选1株夹竹桃，使其株高和地径均为计算得到的平均值，将该植株作为试验的标准株。本次试验共计选取3个龄期的夹竹桃标准株共计9株，植株测量结果如表1所示。

表1 不同龄期夹竹桃标准株选取Table 1 Selection of oleander standard plants at different ages

选取原位拉拔试验标准株后，对3个龄期原位拉拔试验的共9株标准株的株高及地径分别取平均值，得到整株挖掘法的各龄期标准株参数，在研究区内挑选最接近该参数的夹竹桃作为整株挖掘法标准株，采集其根系带回室内进行统计分析。

1.2.2 整株原位拉拔试验

本研究通过对灌木进行原位拉拔试验来探讨植物根系对根土间作用力的影响。采用自行设计的根系原位拉拔装置对植物根系进行拉拔试验，装置如图2所示。该装置由钢丝、拉力传感器、位移传感器、三脚架等组成，具有操作简单、占地少、适用类型广等特点。拉力传感器能记录任意拉拔时刻的拉力，位移传感器能记录拉拔力对应的拉拔位移。三脚架作为施力装置，最大能承受3 kN的拉力，与之配套的拉力传感器能承受5 kN的拉力，且分度值为1 N。

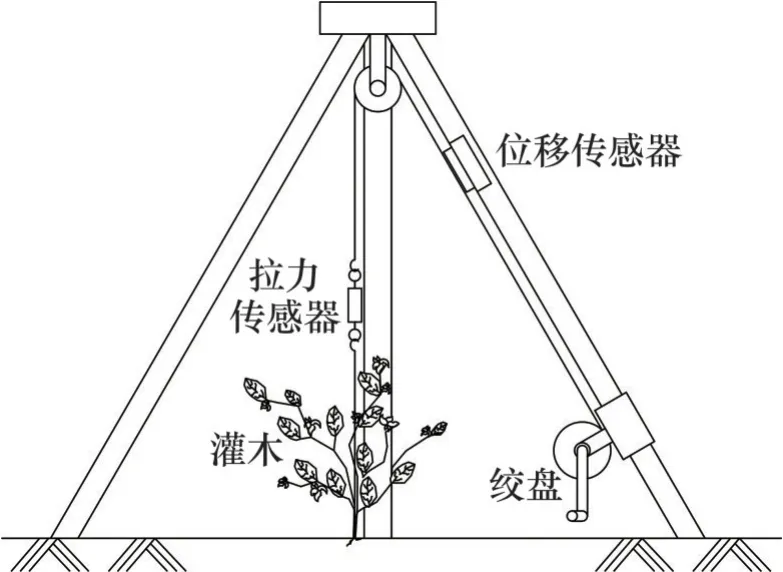
图2 原位拉拔试验装置Fig.2 In-situ pull-out test device

将铁丝或细绳缠绕在灌木植物的茎部，固定牢固后与拉力计挂钩相连接，然后缓慢转动绞盘将整株植物拔出，记录该过程中拉力计的最大读数及拉力-时间曲线。对1、2 和3 a 龄期的植株进行原位拉拔试验，各个龄期确保试验成功3株。试验需要同步测试拉拔力与拉拔位移，且在试验过程中夹具不脱落，只有符合上述条件方可认为试验成功。拉拔完成后，对试验区土体进行环刀取样，用于测定试验区土体参数，同时，将拉拔试验的植物根系放入保鲜袋带回试验室。

1.2.3 单根拉伸试验

采用万能试验机系统进行根系拉伸试验，其中拉力计主要由动力系统、夹具、拉力传感器、位移传感器以及电脑组成，拉力计最大量程为5 kN，分度值为0.1 N。为避免夹具损伤根系而导致根系在夹具附近断裂，试验前在每根根系上、下两端包裹环氧树脂胶。

选取顺直、完整无损、直径相对均一的新鲜根系进行根系拉伸试验。首先，将根系两端固定在夹具中，缓慢施加荷载使根系垂直，然后，用数显游标卡尺在根系两端及中间处各测1次根系直径，并取算术平均值作为该根系直径。接着，启动试验机开始试验，在此过程中，数据采集仪自动记录拉力和位移。本试验要求根系必须从中间部位断裂才算试验成功，若从夹具处滑脱或断裂，则均视为失败。

1.2.4 直剪剪阻试验

根据测得的试验区土体参数，按照GB/T 50123—2019《土工试验方法标准》[18]制备直剪试样。试验使用的直剪仪为南京土壤仪器有限公司生产的ZJ 型应变控制式直剪仪，在直剪仪上盒放入土样，在下盒嵌入表面黏有根系的亚克力板，板的直径与试样直径相同。将根系固定在亚克力板上，使根的轴线方向与受剪方向平行[19]。每组试验取4个试样，试样装好后分别加载。为有效测量根土复合体界面摩阻强度，考虑根系在实际土层中的深度，法向应力σ分别设置为25、50、75、100 kPa，以0.8 mm/min 的速率进行剪切，直至测力计读数随剪切位移的增加不再发生变化或剪切位移达到4 mm，记录对应的最大剪应力τ。将试验结果绘成σ-τ曲线，从而求得根-土界面黏聚力cs和界面摩擦角φs。

2 试验结果与分析

2.1 根系原位拉拔试验

2.1.1 根系最大拉拔力及其变化规律

夹竹桃根系发达，根系沿水平方向发育明显，植株生长速度较快，1 a 龄期植株株高接近1 m。通过原位拉拔试验装置的牵引，夹竹桃完整拔出的形态如图3(a)所示。通过拉拔装置拔出的根系存在完整拔出破坏和拉断破坏共2种破坏模式，如图3(b)所示。

图3 夹竹桃根系破坏形态Fig.3 Damage morphologies of oleander root system

将完成原位拉拔试验的9 株夹竹桃带回室内，统计试验结束后所有根系的破坏形态。统计结果表明：夹竹桃根系较发达，较粗的根系多从根系中部断裂，属于拉断破坏；较细的根系多从土体中完整拔出，属于拔出破坏。这说明在原位拉拔试验过程中，2种根系破坏模式是同时发生的，统计结果如表2所示。

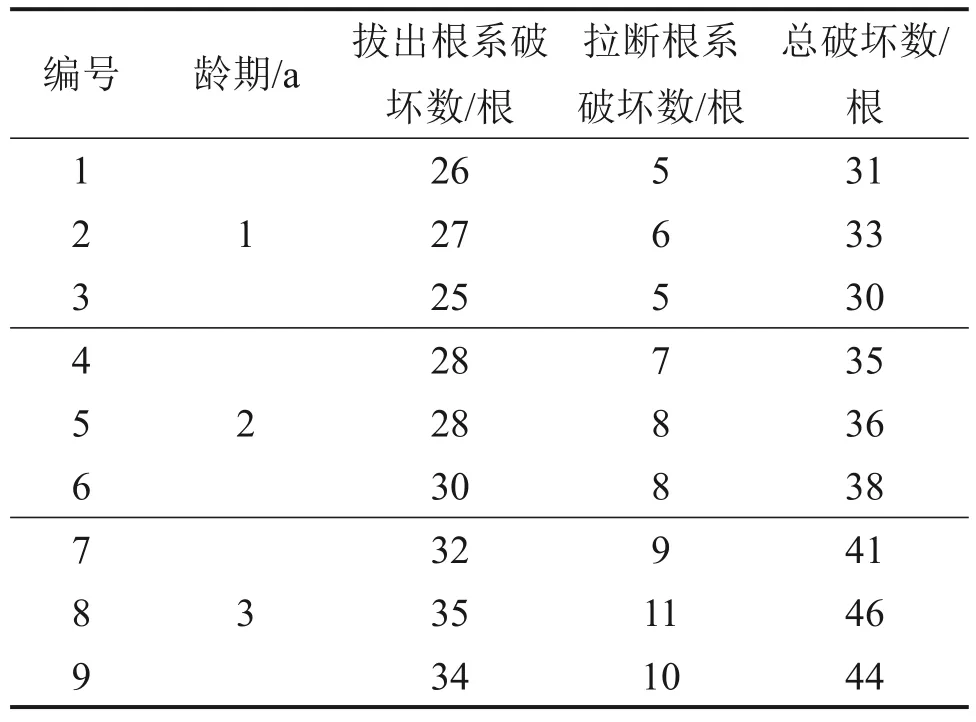
表2 拉拔试验根系破坏形态统计Table 2 Statistics of root failure morphology in pullout test

由表2可知：原位拉拔试验的根系破坏形式以拔出破坏为主，占全部根系数量的76%～84%；1 a龄期的夹竹桃拔出破坏根系占比为82%～84%，2 a龄期占比为78%～80%，3 a 龄期占比为76%～78%；龄期越大，被拔出破坏的根系占比越低。其原因可能是龄期越大，粗根的数量越多，细根占比相对变小，而细根基本上以拔出破坏为主，因此，拔出破坏的根系在高龄期的夹竹桃根系拉拔破坏时占比较小。

2.1.2 根系拉拔力及位移变化规律

试验发现夹竹桃根系的拉拔力平均值为(744.0±447.1) N，根系拉拔力为291.7～1 567.7 N，其中，1 a 生夹竹桃的最大拉拔力平均值为(307.4±16.4) N，2 a 龄期的最大拉拔力平均值为(672.4±181.6) N，3 a龄期的最大拉拔力平均值为(1 253.9±287.8) N。从3 种龄期的夹竹桃拉拔力平均值及方差分析检验结果发现，龄期越大，拉拔力平均值越大。通过整株拉拔试验，获得9株不同龄期的夹竹桃根系拉拔力与位移关系曲线。由于每个龄期曲线形式基本相同，因此，选取表2中2号、6号、8号夹竹桃的拉拔力-位移关系曲线作为1、2、3 a龄期夹竹桃的代表，对以上3种龄期夹竹桃拉拔力-位移曲线进行定性分析，结果如图4所示。

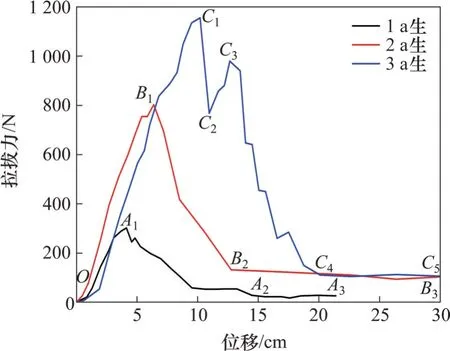
图4 拉拔力-拉拔位移曲线Fig.4 Curves of pull-out force-displacement

由图4 可知：对于不同龄期的夹竹桃整株根系，其拉拔过程存在较大区别，且最大拉拔力和对应的拉拔位移也有所区别；对于1 a 生夹竹桃，OA1段为拉拔作用的初期阶段，根系拉拔力与位移的关系可近似看作呈线性关系，当根系拉拔位移达到4.5 cm 时，达到最大拉拔力306.2 N，继续拉拔根系，此时曲线为图中A1A2段，拉拔力呈现出缓慢下降趋势；当拉拔位移达到14.5 cm时，拉拔力保持不变，说明此时根系已经被完全拔出；对于2 a生夹竹桃，其曲线整体特征与1 a生夹竹桃的曲线整体特征相似，OB1段为线性增加段，B1点对应的拉拔力为根系的最大拉拔力812.5 N，此时，拉拔位移为6.5 cm；B1B2段为非线性减小段，说明此时根系正逐渐被拔出；当曲线到达B2点后，曲线变成1条直线，说明根系已经完全被拔出；对于3 a 生夹竹桃，其原位拉拔曲线存在明显不同，当达到C1点时，曲线短暂下降到达C2点，然后又波动上升到达C3点，且C3点高度小于C1点高度，说明3 a生的夹竹桃随着拉拔位移增加，达到最大拉拔力后还能继续承受拉拔力。试验结果表明：3 a生的夹竹桃原位拉拔曲线与1 a生和2 a生的夹竹桃的原位拉拔曲线存在明显差异，主要体现在3 a生夹竹桃拉拔曲线存在2 个峰值点即C1和C3点，说明其达到最大拉拔力后仍然可以承受拉拔力，而其他龄期的夹竹桃达到最大拉拔力时，根系已经断裂或失去锚固作用，开始滑动，无法继续承受拉拔力。

所获得的9株不同龄期的夹竹桃根系最大拉拔力与峰值位移如表3所示。

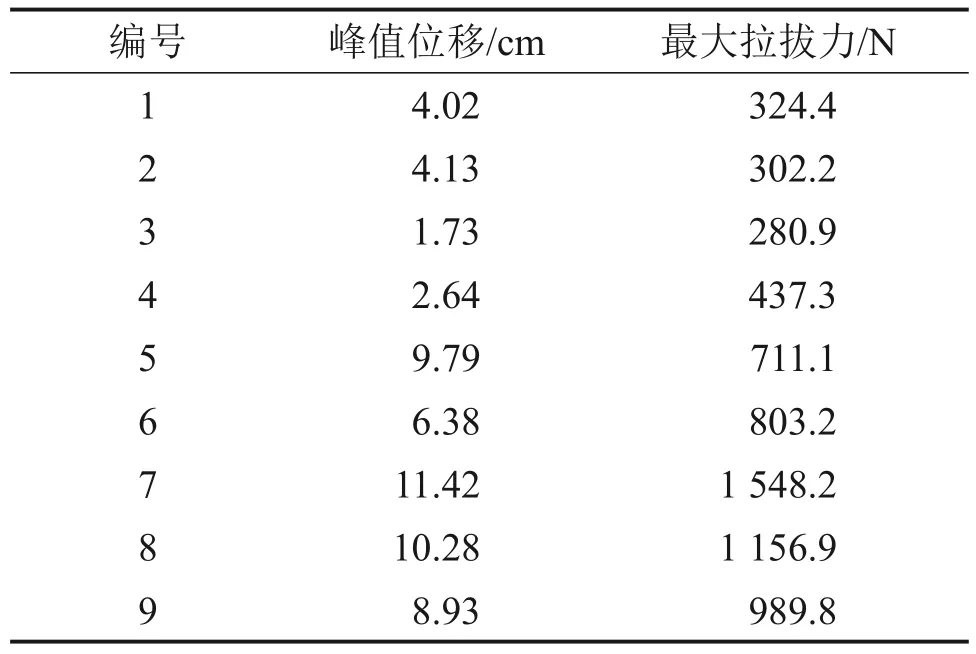
表3 夹竹桃的最大拉拔力与峰值位移Table 3 The maximum pull-out force and peak displacement of oleander

由表3可知：本试验中夹竹桃根系最大拉拔力对应的位移平均值为(6.9±3.6) cm，1 a 生最大拉拔力对应的位移平均值为(3.5±1.6) cm，2 a 生最大拉拔力对应的位移平均值为(7.0±3.5) cm，3 a 生最大拉拔力对应的位移平均值为(10.3±1.5) cm，且3 种龄期的位移平均值存在显著性差异，其原因在于高龄期的夹竹桃根系埋深更深，根系分生层次更多，根系更加发达。通过观察夹竹桃根系。发现其没有明显的主根，且根系的根径较均一，分生层次较少，最多只有3级根，因此，当夹竹桃整株根系受到外力作用时，各个根系分散受力，表现为在拉拔初期，拉拔力随着植株上升急剧增大，当拉拔力达到最大值时，大部分植株根系被拉断，最大抗拉拔力急剧减小；对夹竹桃植株继续施加拉拔力，植株继续向上移动。在这个过程中，部分根系先后被拉断，但由于该部分根系根径较小，对于拉拔力-位移曲线的影响不大，曲线只出现较小波动。夹竹桃的拉拔试验结果均验证了灌木植物根系长度与根系分布的异质性。

已有研究表明[20]，生态防护边坡土体的变形和破坏与根系的变形破坏密切相关。当边坡土体出现浅层蠕滑、溜坍等变形时，穿过滑裂面的灌木会受到土体的牵连作用，根系就会受到拉拔力的作用，因此，当夹竹桃龄期越大时，在相同拉拔位移条件下，拉拔力就越大，其抵抗根土复合体破坏的能力就越强。基于上述推断，在考虑存活率的前提下，应尽量选择龄期较大的植物。

2.1.3 夹竹桃形态学指标与最大拉拔力的关系

由于土地肥力不均以及植株生长发育速度不同，同一龄期的植株长势表现出一定的离散性。与龄期等指标相比，株高、地径、质量等形态学指标更能表征夹竹桃的长势。基于此，对最大拉拔力、夹竹桃植株基本特征与根系形态学参数的相关性关系进行研究。本研究采用前面的灌木形态学参数测量方法，系统探究不同龄期夹竹桃最大拉拔力与形态学指标的关系。3个龄期的夹竹桃形态参数统计结果如表4所示。本研究采用方差分析探讨不同龄期夹竹桃形态参数的关系。从表4可见：在显著性水平为0.05时，3种龄期的夹竹桃的株高、植株质量、地径、根系质量这4个指标存在显著性差异，3 a龄期的形态指标显著高于1 a和2 a龄期的形态指标。

相关性分析是指对2个或多个具备相关性的变量元素进行分析，从而衡量2个变量因素的相关程度，相关系数ρX,Y越趋近于1，表明2 个指标间的关联性越强。为建立夹竹桃形态指标与最大拉拔力的关系，首先，株高对植株最大拉拔力与其形态学指标之间的关系进行相关性分析。株高、植株质量、根系质量、地径与最大拉拔力之间的相关系数R2分别为0.84、0.92、0.86和0.81。

假设存在2组符合正态分布的连续随机变量X和Y，即

式中：xn、yn分别为随机变量X、Y所包含的样本值；n为样本个数。由此，相关系数ρX,Y的计算式为

式中：ρX,Y为变量X与Y的相关系数；cov(X,Y)为变量X与Y的协方差；和分别为变量X和Y的总体方差；E(X)、E(Y)分别为变量X、Y的期望值。

通过对夹竹桃最大拉拔力与灌木形态学指标的相关性分析可知：最大拉拔力与植株质量、根系质量、地径、株高这4个植株形态参数相关性系数分别为0.92、0.86、0.81、0.84，相关系数ρX，Y均超过0.80，相关性明显。其中，拉拔力与植株质量的相关性系数最大，达到0.92，说明这两者存在较强的相关性，可以采用拟合回归的方法得到两者的函数关系，如图5所示(其中，R2为拟合度)。

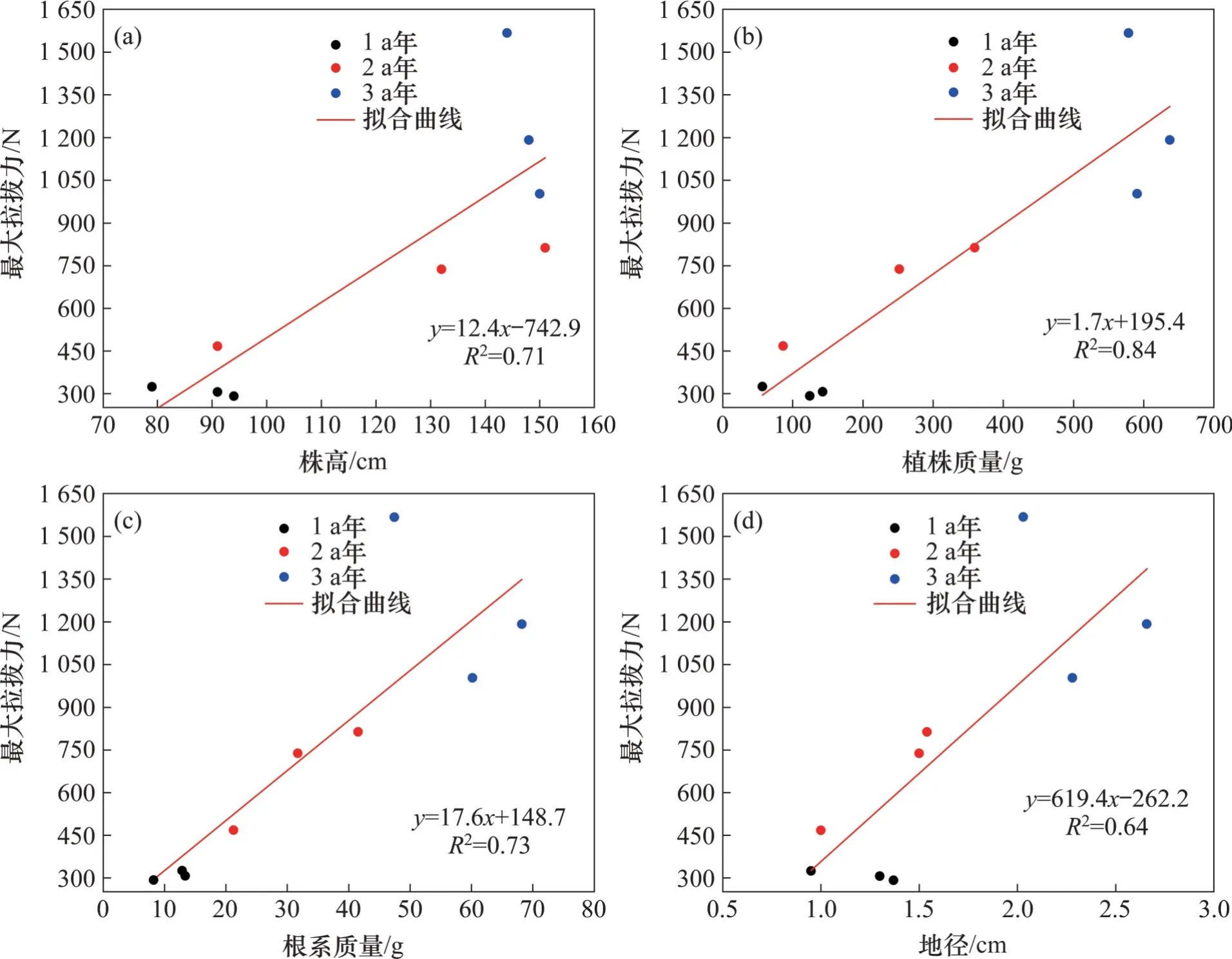
图5 最大拉拔力与植株形态学指标的关系Fig.5 Relationship between maximum drawing force and plant morphological indicators

从图5可知：随着生长期增加，株高、植株质量、根系质量及地径增大，最大拉拔力也随之增大；2 a 龄期的夹竹桃株高和根系质量增幅最大，增大幅度分别达到41.70%和173.91%，3 a 龄期植株增幅分别减小为18.12%和86.03%；2 a龄期夹竹桃植株质量和地径的增幅分别小于3 a龄期的夹竹桃植株质量和地径的增幅(2 a 龄期的增幅只有115.37%和12.50%，而3 a 龄期的增幅则分别达到158.90%和77.85%)。通过对比最大拉拔力的增幅可以发现：株高和根系质量的增幅与最大拉拔力的增幅存在明显正向关系，均在1～2 a这一生长阶段达到最大，但在2～3 a这一生长阶段增幅明显变缓。这是由于夹竹桃根系的生长发育阶段主要集中在2 a内这一阶段，而在2 a以后主要是地上部分生长发育。根系质量增加说明根系的长度、数量增加，根土之间的接触更加紧密，增大了根和土的接触面积，增强了根系与土体之间黏结强度，宏观表现为最大拉拔力增大。

2.2 根系原位挖掘试验

2.2.1 根系径级分布

原位拉拔试验会造成根系在实验过程中断裂，不足以表征夹竹桃根系的完整形态，故采用全挖掘法获取不同龄期夹竹桃的完整根系。夹竹桃根系形态如图6所示。根系被挖掘后，将其置于保鲜桶中带回，对根系数量进行统计，结果如表5所示。

表5 夹竹桃根系数量统计Table 5 Quantitative statistics of oleander root system

图6 夹竹桃根系形态Fig.6 Root morphologies of oleander

由表5可知：不同龄期的夹竹桃生长状况存在极大差别，1 a 生的根系埋深只有21 cm，而3 a 生的根系埋深达32 cm，夹竹桃平均埋深26 cm。将根径分为[0，1)、[1，2)、[2，5)和[5，10] mm共4个径级，其中，[0，1) mm的根系数量占全部根系数量的43.4%，其次是[1，2) mm 的根系，约占30.7%；数量最少的是[5，10] mm 的根系，只占6.1%，并且只在2 a和3 a生的夹竹桃中才出现。

2.2.2 根系质量分布

根系质量沿深度的分布规律能反映出不同龄期夹竹桃根系加固土体的范围。将根系质量按照埋深划分为[0，10) cm、[10，20) cm和[20，+∞) cm进行统计，根系质量占比(对应根系埋深的根系质量与总根系质量之比)统计结果如图7所示。

图7 不同龄期根系质量垂直分布Fig.7 Root Mass distribution at different ages

由图7可知，所有龄期的夹竹桃的根系质量沿深度增加逐渐减小，根系质量集中在[0，10) cm埋深之间，且占比均大于50%。夹竹桃根系没有明显的主根，侧根较发达，土体中须根密集，根系大部分沿水平方向延伸，根系主要分布在40 cm土层内，属于典型是水平根型。所以，夹竹桃加固根系的最佳埋深为[0, 10) cm的土层中。

2.3 单根拉伸试验

2.3.1 根系最大抗拉力

试验测试不同直径的夹竹桃根系20 根，共得到12 个夹竹桃单根最大抗拉力(试验成功率为60%)，如表6所示。试验中根系的破坏形态如图8所示。试验成功的夹竹桃根系直径范围为0.68～4.40 mm，平均值为(2.10±1.03) mm。夹竹桃单根根系最大抗拉力范围为24.2～110.9 N，平均值为(63.5±34.5) N。

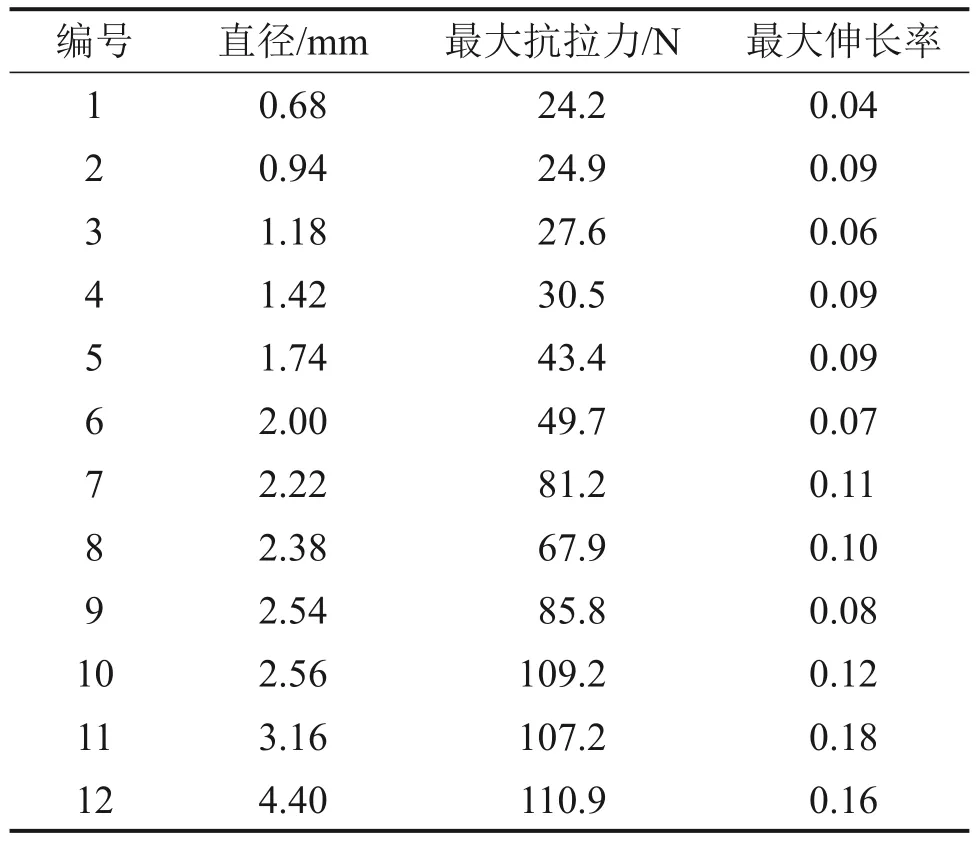
表6 夹竹桃单根的最大抗拉力和最大伸长率Table 6 The maximum tensile resistance and elongation of oleander single root

图8 夹竹桃单根拉伸试验破坏形态Fig.8 Failure morphologies of oleander single root in tensile test

对夹竹桃根系直径与单根最大抗拉力进行方差分析，发现直径与根系最大拉力存在显著性差异(P＜0.05)，此结论与田佳等[21]所得出的结论相同，因此，可以对夹竹桃直径与单根最大抗拉力进行拟合，拟合结果如图9所示。

图9 夹竹桃最大抗拉力与根系直径的关系Fig.9 Relationship between maximum tensile strength and root diameter of oleander

由图9可知：根系的最大抗拉力与直径均呈正相关关系，且单根抗拉力与根径呈幂指数关系；抗拉力随直径增大而增大，说明粗根的最大抗拉力比细根的最大抗拉力大。对图10 中的散点进行拟合，可建立夹竹桃单根最大抗拉力与根径间的幂指数关系：

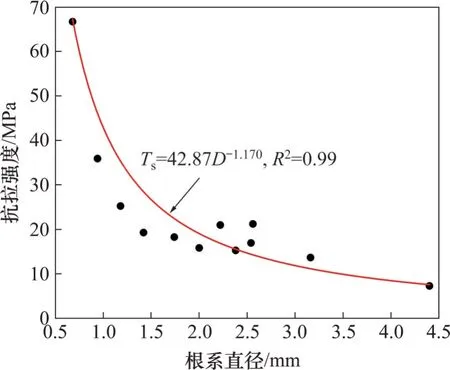
图10 夹竹桃抗拉强度与根系直径的关系Fig.10 Relationship between tensile strength and root diameter of oleander

式中：Fs为根系最大抗拉力，N；D为根系直径，mm；R2为拟合曲线的拟合度，其数值越接近1，拟合程度越高。

此外，常见草本植物及乔木根系拉伸试验也满足上述幂指数关系。陆桂红等[22]通过对寒芒、草地早熟禾等6种草本植物根系进行室内单根拉伸试验发现根系抗拉力与根径间呈幂指数关系，且抗拉力随根径的增加而增大。YE 等[23]通过对百喜草进行单根拉伸试验，也发现单根抗拉力随根径增加呈幂指数增大的变化关系；LATEH 等[24]对乔木进行了单根拉伸试验，也得到了单根抗拉力随着根径增加呈幂指数增大的变化关系。

2.3.2 根系抗拉强度

抗拉强度是植物根系固有的力学属性，反映根系在拉力作用下抵抗破坏的能力。将表2中的数据进行处理，得到根系抗拉强度与直径的关系，如图10 所示。试验测得的根系抗拉强度随根径的增加呈幂指数降低的变化规律，其拟合函数公式如下：

式中：Ts为根系抗拉强度，MPa。

由图10 可知：试验区夹竹桃根系的单根抗拉强度与根径呈幂指数关系，且表现为单根抗拉强度随根径增加而减小的变化规律，单根抗拉强度为7.3～66.7 MPa，平均值为(23.0±15.4) MPa；当根系根土复合体受到剪切作用时，根系会产生拉力，增强了根土复合体的抗剪强度。因此，根系抗拉强度越大，根土复合体抗剪强度越大，从而表现出更显著的固土护坡作用。此外，当根系直径小于2 mm时，夹竹桃的单根抗拉强度较大，且随着根径增大，其单根抗拉强度明显下降；当根径大于2 mm时，随着根径增大，其单根抗拉强度下降幅度不明显。研究结果表明，灌木植物根系深而粗，若根系深入深层较稳定土层中，则可将浅层根系周围土层锚固至深层处较稳定土层中，起到进一步提高边坡浅层土体稳定性的作用。

2.3.3 单根拉伸应力-应变关系

本试验中选择夹竹桃单根拉伸试验结果，绘出[0，1)、[1，2)、[2，3)和[3，4] mm 这4 种径级的夹竹桃根系应力-应变关系曲线，如图11 所示。图11 中，纵坐标为根系单位面积上所承受的拉应力，即单根拉伸过程中根系的抗拉力与根系面积之比，单根的最大拉应力就是其抗拉强度；横坐标为应变，指的是拉伸位移与初始根系长度的比值，即单位长度上的根所发生的变形。

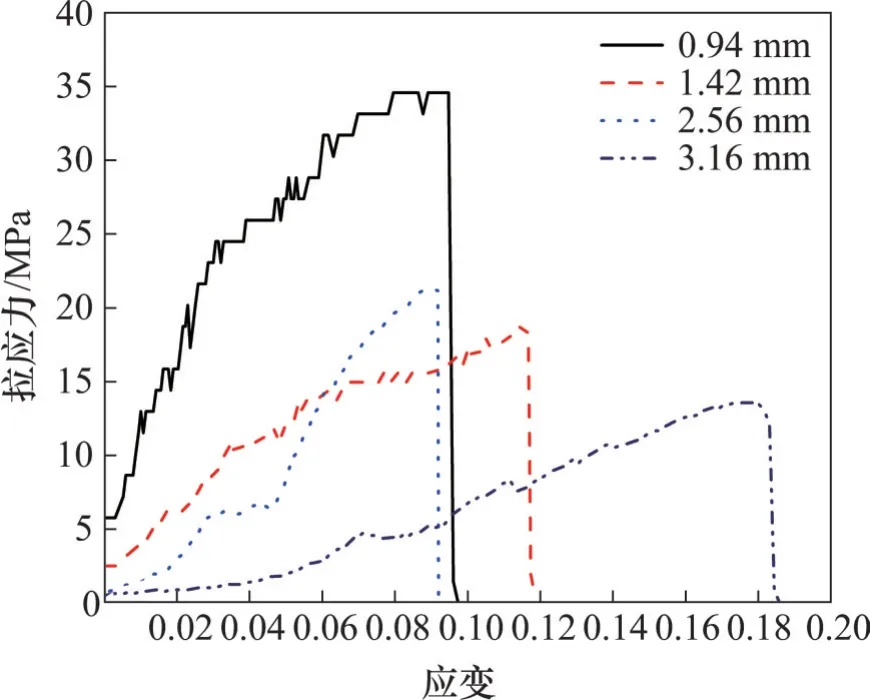
图11 单根拉应力-应变曲线Fig.11 Single tensile stress-strain curves

由图11可知4种径级的夹竹桃单根应力-应变关系表现出不同的特征，主要表现在：4种径级的夹竹桃在单根受拉的初期阶段，应力-应变呈线性关系，表现出弹性材料的特征；当夹竹桃单根拉应力达到峰值时，表明单根承受拉应力的能力达到极限状态，处于该状态下的峰值即为该径级下抗拉强度，当单根承受的拉应力超过该值时，单根立即发生断裂，断裂后拉应力则迅速下降至0 MPa。将最大抗拉力对应的应变定义为最大伸长率，则根据实验曲线得到的最大伸长率如表6所示。

由表6 可知：夹竹桃根系最大伸长率范围为0.04～0.18，平均值为0.10±0.04。对根系直径与最大伸长率进行回归分析，发现随着根径增加，夹竹桃根系的最大伸长率增大，表现出不同于羊蹄甲、灌木[25]的最大伸长率变化规律。结合文献[26-28]，夹竹桃单根抗拉强度与根系细胞间空隙面积呈正相关关系。当单根直径增大时，根系胞间空隙面积增大，而空隙无法承担外荷载，从而表现为单根抗拉力随径级增大而减小。夹竹桃单根最大伸长率与薄壁细胞的数量呈正相关关系，当单根直径增大时，薄壁细胞中富含纤维素含量越高，纤维素的存在提高了细胞的延展性，从而表现为根系的伸长率越大。

2.4 直剪剪阻试验

选取3 种不同龄期的直径为2 mm 的根系表皮进行试验，同时，设计素土剪切试验进行对照。试验结果表明：不同龄期的根-土界面的剪应力-位移关系曲线均无明显峰值，表现为应变硬化。取剪切位移为4 mm 所对应的剪应力为抗剪强度，将直剪剪阻试验结果进行线性拟合，结果如图12所示。

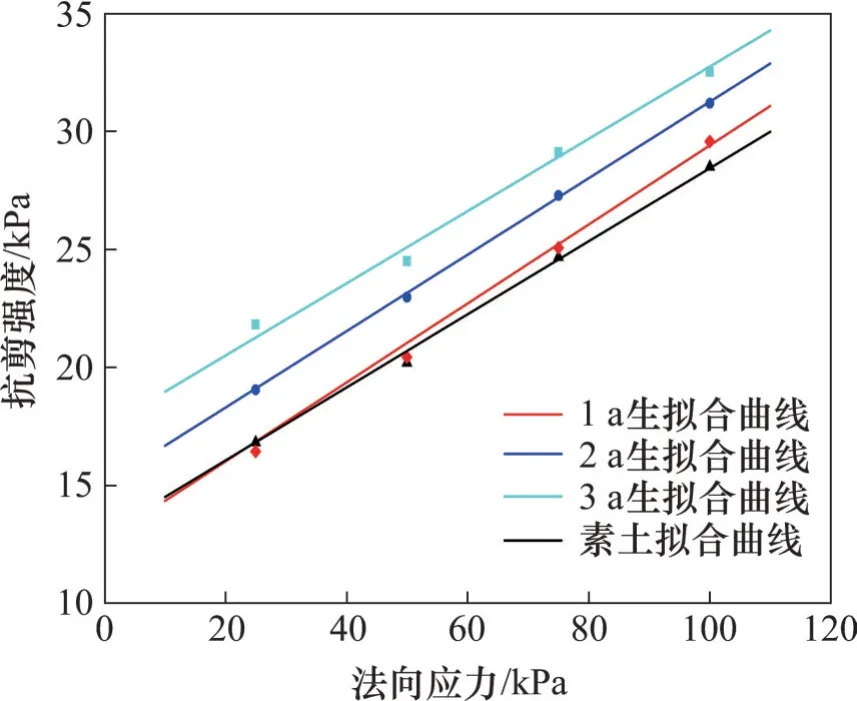
图12 试样抗剪强度与法向应力的关系Fig.12 Relationship between shear strength and normal stress of specimen

由图12 可知，不同龄期的根土界面抗剪强度与界面法向应力均呈线性关系。根据文献[29]可知，根土复合体的界面抗剪强度可用界面摩擦角φs和界面黏聚力cs进行描述，界面抗剪强度参数如表7所示。

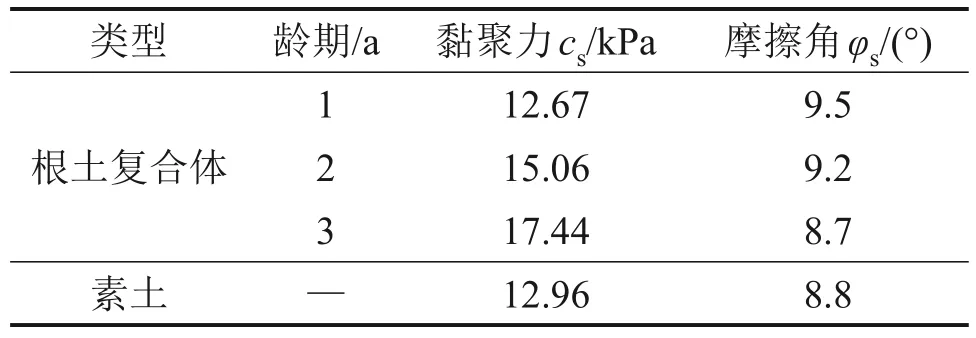
表7 根土复合体界面的抗剪强度参数Table 7 Shear strength parameters of root soil composite interface

从表7可知：不同龄期的夹竹桃根土复合体的界面抗剪强度存在一定差异，具体表现为龄期越大，根土复合体的界面黏聚力越大，但界面摩擦角变化不大，而且根土复合体的界面黏聚力和摩擦角均大于素土的黏聚力和内摩擦角，这说明随着龄期增加，根土复合体抵抗剪切作用的能力增强，其界面抗剪强度增大。

3 整株拉拔力估算

3.1 模型推导

常见的根系固土模型WU模型假定根土复合体在变形过程中所有根系被拉伸，在根系受拉达到极限状态时，所有根系同时瞬间断裂，导致该模型计算值较试验值高640%～1 430%[30]。而纤维束模型虽然假设根系在土体中渐进断裂，但认为根系的破坏是达到抗拉强度的结果，因此，纤维束模型的计算结果也会比实际值高60%～110%。由于此类模型假定与根系实际失效情况不符，因而，此类模型的应用并不广泛，应用的植物类型也不丰富。

根土复合体受到剪切时，最终破坏模式只有拔出和拉断共2 种，而且在整株拉拔试验过程中，这2种根系破坏模式是同时发生的，因此，整株根系的拉拔力应为根系抗拔力和抗拉力之和，即

式中：F为整株根系的拉拔力，N；P为拔出破坏的根系所提供的拔出力的总和，N；T为拉断破坏的根系所提供的抗拉力的总和，N；m和n均为拉拔力的分配系数。

常见模型中假设根土复合体破坏时所有根系均达到抗拉强度并发生拉断破坏，然而，在根土复合体实际破坏时，存在某些根系在达到抗拉强度前已经发生拔出破坏。当根-土界面间的黏结强度较小时，一些根系会在拉断之前被拔出。由于根系是自然生长而非直立生长，最大抗拉力较小的细根首先从土体中被拉出，在拉拔过程中根系与土体黏结，当拉拔力超过土体与根系间的黏结力时，根系与土体间的黏结关系被破坏。因此，根系所受的拉拔力还取决于根-土界面间的黏结强度，而黏结强度与土体应力、根长、根系夹角等因素密切相关。

本文根据以下假设建立根土复合体拉拔模型：

1) 分析根土力学作用时，将三维的根系分布简化为二维分布；

2) 根土复合体可看作土体和根系共同组成的复合结构，根系相当于其中的受拉构件；

3) 当整株根系达到极限状态时，单根同时被瞬间拔出或拉断。

通常认为单根的拉断与拔出破坏均与根系直径D有关。对于拉断破坏，一般认为单根最大抗拉力Fs及抗拉力总和T需满足：

式中：Fs为单根抗拉力，N；a和b均为系数。

对于未达到抗拉强度而出现的根系拔出破坏，当根土复合体中的根系受到拉拔力作用时，根系与土体存在相对运动的趋势，根土界面的摩擦黏结作用将阻止根系的相对运动趋势，使得根土复合体中根系受到界面抗拔力，从而起到抵抗根土复合体破坏的作用。拔出破坏的受力如图13所示，当单根达到抗拔强度时发生拔出破坏，此时抗拔强度τs应满足[31]

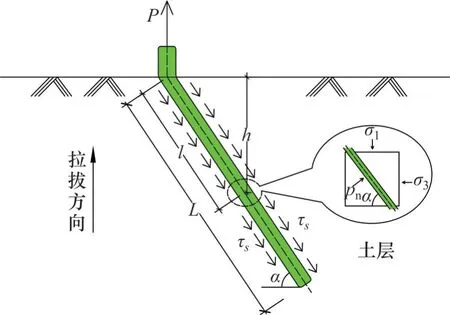
图13 根系拔出破坏的受力分析Fig.13 Force analfsis of root pull-out failure

式中：cs为根土界面黏聚力，kPa；pn为界面法向应力，kPa；φs为界面内摩擦角，(°)。

界面黏聚力cs是由于根土间水及化学物质胶结等作用而产生的，当根系在土体内部滑动时，根-土界面黏聚力失效。根系表面粗糙、凹凸不平[15]，部分土颗粒嵌入根系表面的凹凸部分，当根系与土体产生相对滑移或有相对滑移趋势时，根-土界面间的机械咬合便会产生界面摩阻力fs，其大小由界面法向应力pn与界面摩擦角φs决定，而界面法向应力受土体性质及根系入土角度控制。

采用土中一点应力状态进行分析，不考虑根系直径的影响，令σ1=γh，σ3=k0σ1，则根-土界面法向应力Pn为

式中：γ为土体重度，kN‧m-3；h为计算根段埋深，m；k0为土体静止侧压系数，可通过公式k0=1-sinφ确定；α为根系与水平方向夹角，(°)。

根系拔出破坏的受力分析如图13 所示，计算根段长度与根段埋深的关系满足h=lsinα，此时，单根抗拔力Ps为沿根系长度L方向的界面力的积分：

令a=sinα‧(1+k0+cos2α-k0‧cos2α)‧tanφs，则

通过根系直剪摩阻试验，得到式(9)中夹竹桃根系的界面摩擦角φs=9.05°±0.37°，界面黏聚力cs=(14.53±2.21) kPa。基于根土复合体拉拔模型假设，对表3中不同龄期的夹竹桃按照所有根系均产生拔出破坏和均产生拉断破坏这2种情况进行计算，所得结果如表8所示。

表8 2种根系破坏模式对比Table 8 Comparison of two root failure modes

由表8可知：假设整株根系破坏时所有根系被同时拔出，则其拉拔力计算值比实际值低。假设整株根系破坏时所有根系同时被拉断，则其拉拔力计算值远高于实际值，此结论与田佳等[30]所得出的结论一致。对拉拔试验完成的根系进行统计分析，发现灌木根系在拉拔过程中，根系拉断破坏与拔出破坏同时存在，且拔出破坏模式的根系数量占比为76%～84%，因此，可近似将80%作为夹竹桃整株根系抗拔力的分配系数，即m=0.8，n=0.2，此时，式(6)可改写为

利用式(14)可得到整株挖掘法的根系拉拔力计算值，将其与表3中的拉拔力实际值进行对比，结果如图14所示。

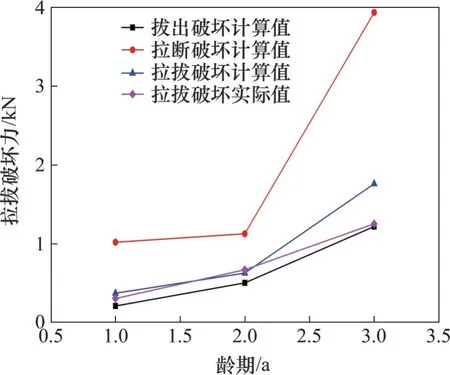
图14 不同龄期拉拔破坏计算值对比Fig.14 Comparison of calculated values of pull-out force of drawing failure at different ages

由图14可知：根据式(14)所得拉拔力计算值与实际值较接近，对于1 a 龄期的夹竹桃，这2 个数值的相对误差为6.2%，对于2 a龄期的夹竹桃，其相对误差为21.9%，对于3 a 龄期的的夹竹桃，其相对误差为40.6%。可见采用本文公式在估算较低龄期的夹竹桃时，拉拔力计算值与实际值最接近。

3.2 讨论

3.2.1 模型参数的确定

1) 根土复合体界面强度参数。根土复合体界面强度参数包括界面摩擦角φs和界面黏聚力cs，是估算根系抗拔力的必要参数，这2种参数可以通过室内根系直剪摩阻试验获取。

2) 根系的抗拉力学参数。根系的抗拉力为单根抗拉力的总和，单根的抗拉力随根系直径D的增大而增大。单根抗拉力可通过单根拉伸试验获得，也可通过经验公式得到近似获得。

3) 根系的形态参数。所需根系形态参数包含数量参数和尺寸参数，其中根系数量为发生拔出破坏的根系数量和发生拉断破坏的根系数量，根系尺寸为单株植物所有根系的直径D和长度L。上述参数可以通过全挖掘试验后人工测量挖出的根系获得。

3.2.2 模型适用范围

1) 根系的力学假定。由于根系刚度较小，因此，可认为根系在根土复合体破坏过程中只承受拉力作用，相当于柔性受拉构件。通过拉拔试验施加的外力在根系中的分布沿根系的轴线方向，即假设根系横截面上只存在轴向拉应力，不考虑弯曲应力和剪应力，因此，本文模型适用于根系刚度较小的草本植物及灌木根系，对于大型植物例如树木的根系的受力并不适用。

2) 根系的几何形态。估算模型中未考虑根系的分支情况，认为每个根表面粗糙且不存在分支，根的顶部与茎部连接，根系沿茎部呈360°对称分布，简化为直径均一的圆柱体，当根土复合体被破坏时，所有根系同时达到最大拉拔力并且发生破坏。因此，模型适用于根系形态为散生根型的草本植物或灌木，对于具有粗壮主根的垂直根型植物并不适用。

4 结论

1) 低龄期的的拉拔力-拉拔位移曲线只有1 个峰值，而3 a 龄期的曲线出现2 个拉力峰值。将夹竹桃根系的整株最大拉拔力与株高、植株质量、地径、根系质量进行相关性分析，发现其均有明显的相关性，通过线性拟合公式能够很好地反映夹竹桃植物形态学指标与拉拔力的对应关系。

2) 根系的抗拉强度随直径增大而减小，而最大抗拉力随直径增大而增大。夹竹桃根系达到抗拉强度对应的应变为最大伸长率，最大伸长率随根系直径增加而增加，与最大抗拉力的变化趋势相同。

3) 夹竹桃根系的生物量分布随龄期增加而增加，且大部分沿水平向分布，生物量集中于[0, 10) cm的埋深范围内，不同龄期的生物量均达50%以上；低龄期的夹竹桃埋深不超过30 cm，而3 a 生高龄期的夹竹桃埋深则可接近40 cm。

4) 以根系拔出和拉断这2 种破坏模式为基础，建立了根土复合体拉拔力学模型。模型考虑了根系摩阻特性，并可对抗拔力进行估算。通过单根拉伸试验和直剪摩阻实验获取模型拉拔力实验值，代入模型得到的拉拔力计算值与拉拔力实际值相符，验证了模型的合理性。采用本文模型能够评价不同类型植物的固土护坡能力，有助于对不同地区护坡植物的类型进行选择。