核心问题引领下的小学数学单元整体教学策略
2023-08-07邵毓清
文/邵毓清
引 言
随着数学教学改革的深入推进,单元整体教学已然成为课程开发和教学实施的基本方式。核心问题指向数学知识本质,是单元整体教学的关键。教师抓住核心问题,可以联结不同的课时内容,建构单元整体,助力学生结构化地理解知识。在探究核心问题时,学生会聚焦学习重点,充分发挥自主性,迁移已有认知,不断探索问题,深度理解和迁移学习内容,拓展学习深度。由此可见,在小学数学教学中,教师要基于整体教学,提炼核心问题,并以此为基础,确定单元整体内容,明确单元目标,搭建问题体系,创设学习活动,引导学生体验活动,解决问题。以“多边形的面积”为例,教师可如此开展单元整体教学活动。
一、提炼核心问题
核心问题指向知识本质。数学知识本质包括数学思想方法、数学基本活动经验等[1]。一般而言,核心问题具有开放性,可以让学生获得主动探究的机会。尤其,在主动探究的过程中,学生会迁移数学认知,解决不同的问题,发现知识点间的内在联系,由此实现整体建构,拓展学习深度。对此,在数学单元整体教学中,教师要剖析教学内容,横向对比,把握联系,就此提炼出核心问题。
“多边形的面积”是苏教版小学数学五年级(上册)第二单元内容。本单元由“平行四边形的面积计算”“三角形的面积计算”“梯形的面积计算”“实践活动:校园的绿化面积”构成。在探究平行四边形、三角形、梯形的面积公式时,学生要使用剪切、平移、旋转等方法,将原图形转化为熟悉的平面图形,之后,对比转化前后的图形,发现它们之间的关系,并以此为基础,推导出平行四边形、三角形、梯形的面积公式。整个推导过程以“转化”为重点。在学习本单元时,学生要掌握转化法。学生掌握转化法,可以“随意”推导其他平面图形,如组合图形、圆形等图形的面积。因此,转化法是本单元的教学重点。于是,教师便可以转化法为重点,同时结合单元教学内容,提炼出核心问题——如何计算未知面积公式的图形的面积?
二、确定单元内容
单元内容是实施单元整体教学的基础。目前,各版本教材章节与课程标准主题划分一致。课程标准主题和单元章节是确定单元整体教学内容的依据[2]。核心问题是单元整体教学的核心。在参照课程标准主题和单元章节时,教师还要审视核心问题,整合相关内容,夯实单元整体教学基础。
苏教版小学数学教材在本单元主要设置了三项内容:平行四边形的面积计算、三角形的面积计算和梯形的面积计算。在学习这三项内容之前,学生要了解面积的内涵、“出入相补”原理,以及平行四边形、三角形、梯形的高。在学习该内容后,学生要综合运用,解决相关的数学问题。同时,学生要尝试迁移经验,探索其他平面图形的面积计算方法。对此,教师可以打破教材限制,重整单元整体教学内容,具体内容见表1。
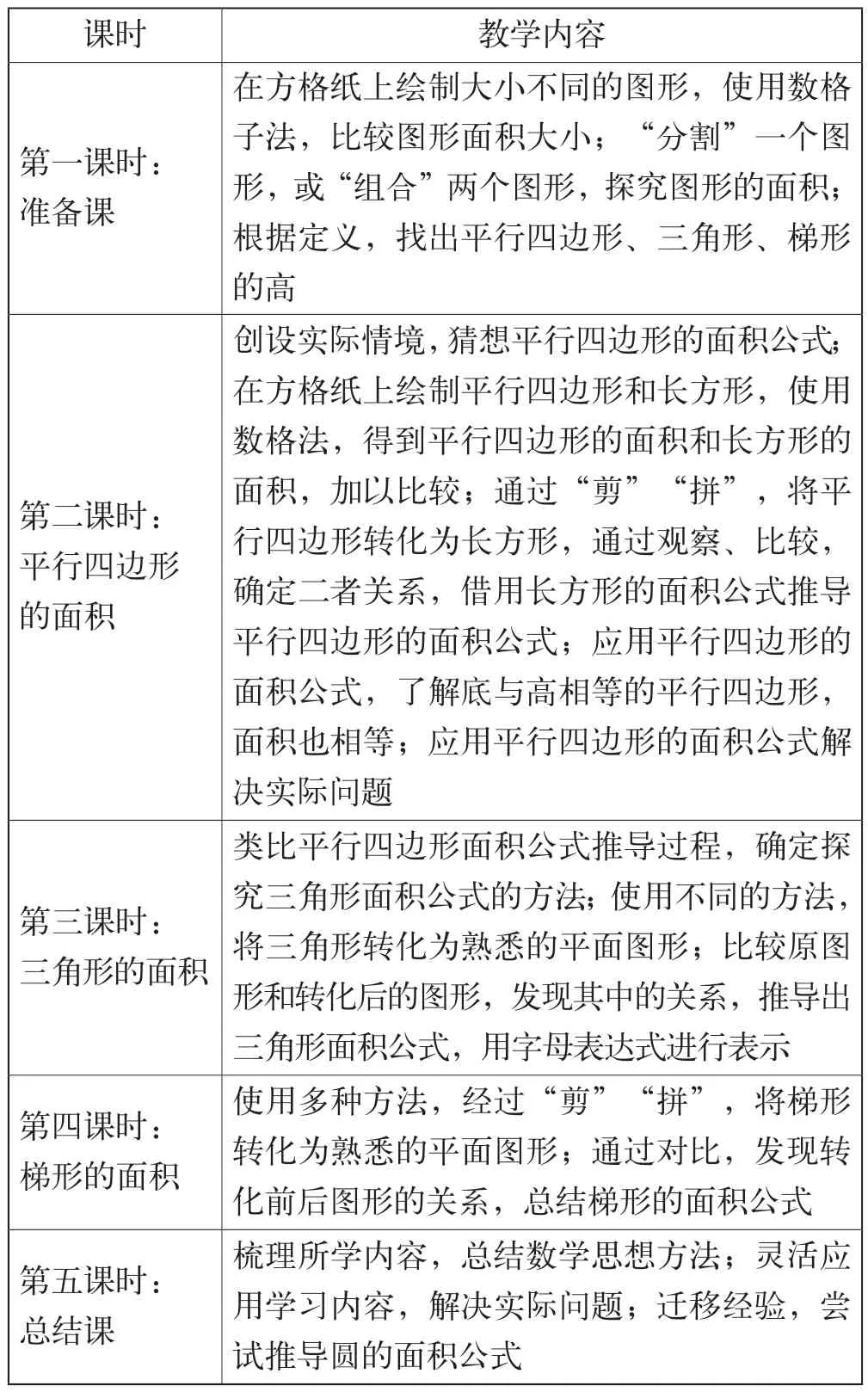
表1
这样有助于教师知道“教什么”,增强单元整体教学的针对性。在如此内容的支撑下,学生会站在整体角度积极思维,踊跃探究,掌握数学知识,获取数学思想方法,把握知识点之间的联系,建构知识结构。
三、设计单元目标
单元目标包括单元整体教学目标和课时教学目标。在明确的单元教学目标的作用下,教师可以明确“教什么”“如何教”以及“教到何种程度”。解决核心问题是学生参与单元整体教学的目的之一。同时,学生在参与单元整体教学的过程中,要顺其自然地发展数学学科核心素养。因此,教师要结合数学学科核心素养、核心问题以及单元整体教学内容,设计单元整体教学目标和课时教学目标,做好单元整体教学准备。
在“多边形的面积”单元整体教学中,教师设计了如下教学目标,具体见表2。

表2
在如此教学目标的指引下,教师将围绕教学内容组织相关活动。学生在体验活动时,会发挥自主性,灵活迁移、应用,探究、掌握数学知识点,尤其数学思想方法,发展数学学科核心素养。
四、搭建问题体系
解决核心问题是单元整体教学的重中之重。问题引领是解决核心问题的关键。在问题的引领下,学生会不断思维,逐步解决核心问题,掌握核心内容。此外,问题是数学教学内容与数学学习活动之间的桥梁。有效的问题可以推动单元整体教学活动顺利开展。学生通过体验学习活动,可以掌握数学内容。所以,在单元整体教学中,教师可以结合核心问题和课时内容,搭建问题体系。
在“多边形的面积”单元教学中,教师可以紧扣核心问题,梳理课时内容,设计相关的主问题和问题串,搭建问题体系(见表3)。
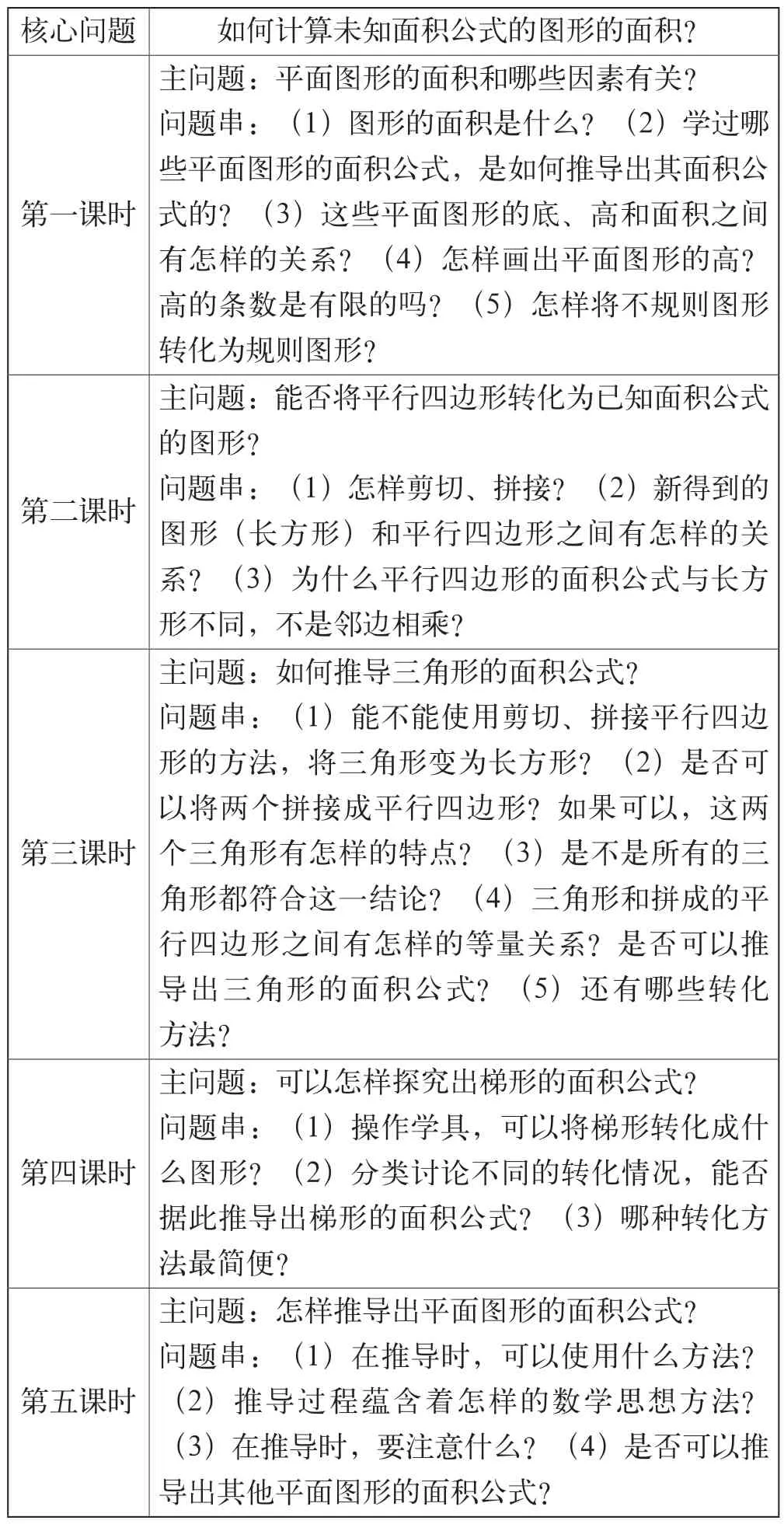
表3
在实施各课时教学时,教师要以主问题为中心,以问题串为线索,串联相关的学习活动,驱动学生积极体验。
五、创设学习活动
学生在体验实践活动时,会发挥主观能动性,开动脑筋,积极思维,迁移应用已有认知,使用多样方法,逐步解决问题串、主问题和核心问题,掌握知识本质,实现深度学习。基于此,在数学单元整体教学中,教师要依据核心问题以及课时问题,发挥教学智慧,创设适宜的学习活动。
以“多边形的面积”第二课时为例,在这节课上,教师组织了数格子活动、剪切活动、对比活动和应用活动。例如,在组织“数格子活动”时,在课堂上教师采用开门见山的方式,直接向学生提出主问题:“能否将平行四边形转化为已知面积公式的图形?”面对此问题,大部分学生陷入思维困境。教师可以把握时机,为每个学生发放方格纸,鼓励学生数格子,得出关于平行四边形和长方形的数据与结论。在体验数格子活动时,大部分学生兴致高昂,迁移已有认知(数格子经验),使用恰当的方式数出平行四边形和长方形所占的格子数,并建立表格,梳理底(长)、宽、面积。之后,学生认真观察、对比,发现平行四边形和长方形之间的关系。有学生说道:“平行四边形的底等于长方形的长,平行四边形的高等于长方形的宽。它们的面积也相等。”基于此,教师鼓励学生猜想平行四边形的面积公式。大部分学生联想长方形的面积公式,提出猜测——平行四边形面积=底×高。于是,教师趁机组织剪切活动,鼓励学生验证猜想。在操作时,大部分学生回想数学所学(通过平移将不规则图形转化为长方形),尝试将平行四边形转化为已知面积公式的图形。在此过程中,教师提出系列问题,如“怎样剪切、拼接?”“新得到的图形(长方形)和平行四边形之间有怎样的关系?”在问题的驱动下,学生边操作边思考,解决问题。
实践表明,学生通过体验实践活动,灵活迁移已有认知,积极探究,不断解决问题,掌握了数学知识和数学思想方法,锻炼了思维能力、应用能力。
结 语
总之,在小学数学教学中,教师要研读教学内容,提取核心问题,并以此为基础,整合有联系的知识点,建构教学单元,继而设计单元教学目标,搭建问题体系,创设学习活动,驱动学生积极体验。学生在体验活动时,会受到问题的驱动,积极思维,迁移已有认知,使用不同的方法解决问题,掌握知识,把握知识点之间的联系,建构知识结构,顺其自然地发展数学学科核心素养。
