“双减”政策下的小学数学作业分层设计研究
2023-08-07周伯全
文/周伯全
引 言
凭借诊断、巩固和分析学情优势,作业一直备受基础教育重视,但这也带来了一个问题——为发挥作业功能,一些教师为学生布置了过多作业。为减轻学生压力,“双减”政策出现了。
一、“双减”政策解读及其对小学数学作业的影响
“双减”政策不仅提出了“全面压减作业总量和时长,减轻学生过重作业负担”的要求,还对健全作业管理机制,提高作业设计质量表明了一些办法,如“加强学科组、年级组作业统筹”“鼓励布置分层、弹性和个性化作业”“坚决克服机械、无效、重复性、惩罚性作业”等,在优化小学数学作业方面发挥着举足轻重的作用。
二、在“双减”政策下优化小学数学分层作业的策略
(一)减量:用心备题
1.改进备题方式
“双减”指出,健全作业管理机制是减轻学生过重作业负担的重要内容,学科组、年级组应统筹管理作业。在此背景下,教师设计小学数学分层作业,可以改进以往独立备题方式,融入“集体备课”思维,建立“三备”备题模式,即教师首备、集体备、个人复备[1]。
2.调整备题目标
“双减”政策落地,不仅是为减轻学生过重的作业负担和校外培训负担,更是为让每一名学生都得到最优的发展。而让学生持续巩固数学知识,并不能达到此目标。所以教师在设计分层作业时,还要调整备题目标,避免让作业内容只停留在知识点记忆的考查层面,要重视数学学科核心素养的渗透。
(二)提质:细心选题
1.多类型
选择题、填空题、判断题、解答题、画图题、列式题,都可以成为小学数学分层作业的题型要素,并且能在题型的变化中,减少“做作业”乏味感,提高学生“巩固学习”的乐趣。以人教版数学三年级下学期“长方形、正方形面积的计算”一课为例,多类型分层作业设计思路如下。其中,选一选、填一填均为基础题,可以满足全体学生作业需要,而画一画中,长方形存在多种画法,使面积有所不同,考验学生灵活画图能力,是对基础层学生的一种挑战,也有利于培养发展层学生发散的数学思维。至于算一算,题目存在两种不同解法,能够在考验基础层、发展层学生的同时,锻炼拔高层学生“一题多解”能力。以下为习题设计:
(1)选一选
一个长方形的长是7.5 米,宽是6.2 米,它的面积是( )。
A. 465 平方米 B. 46.5 平方米 C. 4.65 平方米
(2)填一填
用4 个边长是3 厘米的小正方形拼成一个大正方形,这个大正方形的周长是( ),面积是( )。
(3)画一画
在方格纸(如图1)上,分别画出一个周长为20的长方形和正方形,并计算其面积。(每个方格的边长为1 厘米)

图1
(4)算一算
求下面图形的面积(如图2)
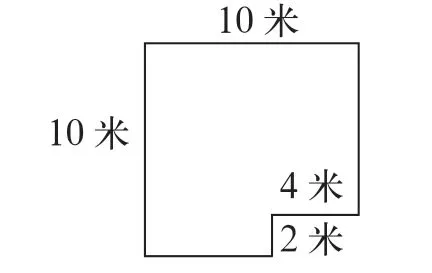
图2
2.抓重点
抓住重点,基于学生数学水平差异设计典型题,不仅可以达到“坚决克服机械、无效、重复性、惩罚性作业”目的,还能强化学生对学习重点与难点的巩固。为此,基于“双减”政策,教师应在紧扣学情前提下,深研教材与课标重难点,确定分层作业重点[2]。
例如,人教版数学四年级上学期“梯形的认识”一课,教材以掌握梯形的特征、知道梯形的各部分名称、会画梯形的高为重点。课程标准强调,学生能说出梯形的特征,说出图形之间的共性与区别,形成空间观念和初步的几何直观。由此,定位“探究梯形特征”“画梯形的高”两个重点。在设计分层作业时,教师可安排难度不同的“说梯形特征”与“画高”题目,突出几何探究,加深不同水平学生对梯形的几何直观认识。
“梯形的认识”分层作业典型题(重点)示例:
(1)智慧填空
______相等的梯形叫作等腰梯形。
(2)聪明断案
梯形的高和底一定是互相垂直的。( )
(3)神笔会画
画出以下梯形(如图3)的高,并标出上底、下底和腰。
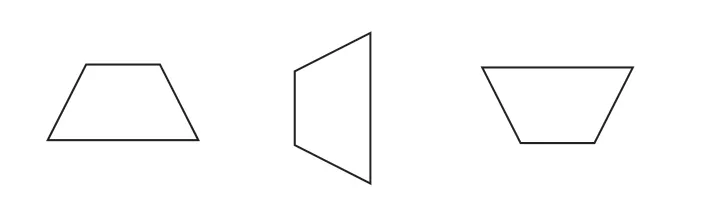
图3
题目紧扣“梯形的特征”与“画梯形的高”展开,由“梯形的高一定比腰短”,考查学生对梯形特征的认识能力和逻辑思维能力。特别是在“神笔会画”板块,梯形以不同形式呈现,画高难度截然不同,自然地满足了不同层次学生“巩固重点”的学习需要。
(三)增效:精准命题
1.前置分层作业
对于基础层、发展层、拔高层三类数学水平处于不同层次的学生来说,前置作业功能是有一定区别的。例如,基础层前置作业,以激发兴趣,了解新课为主,发展层前置作业,以认知基础内容,增强探究热情为主,拔高层前置作业,以培养自学能力,促进课堂翻转为主。
“圆的面积”前置分层作业
(1)开动脑筋
根据教材导学情景图(此处略)思考,圆形草坪占地面积实际是求什么图形的面积?这个图形的面积应该怎样进行计算?
(2)小试牛刀
能不能把圆转化成曾经学习过的图形,从而推导出圆面积的计算方法?
(3)锋芒初现
圆的面积公式是什么?
一个圆形草坪的直径是20 米,每平方草皮8 元。自主运用圆的面积公式,完成问题:“这个圆形草坪的面积是多少平方米?”“用草皮铺满这个草皮,需要花多少钱?”
2.随堂分层作业
由于对新课的接受程度不同,不同水平学生对随堂作业的需求也存在差异。教师同样应对小学数学随堂作业进行分层设计。在此基础上,教师还应加强对随堂作业的面批讲解,做好答疑辅导。
“圆的面积”随堂分层作业
(1)快速填空
把一个圆平均分成若干等份,可以拼成一个近似的______,这个图形的长相当于______,宽相当于______,可以推导出圆的面积公式是______。
一个圆的半径是4 分米,面积是____。
如果一个圆的直径扩大3倍,半径会扩大______倍,面积会扩大______倍。
(2)看图计算
求下列圆(如图4)的面积(注意区分直径与半径)
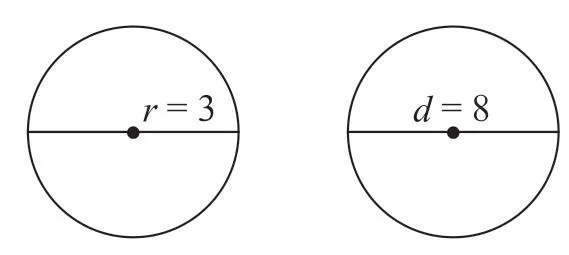
图4
(3)解决问题
一个直径为4 米的圆形养鱼池占地面积是多少平方米?
一个运动场两端是半圆形,中间是长方形。已知长方形的长为100 米,圆的半径是32 米,这个运动场的面积是多少平方米?
在作业中,快速填空难度最小,看图计算到解决问题,难度逐渐增大,考查学生在实际情境中推理和解决问题的能力,由低到高地满足不同水平学生的需要。对于学生因马虎、基础掌握不扎实等原因出现的错误,教师可以及时纠正,最大限度地利用课堂时间,达到让学生有效查缺补漏的目的。
3.课后分层作业
课后作业的目的在于增强学生课后复习意识,使学生在复盘所学内容、解决复杂问题的过程中,持续提高数学学习和实践能力,避免课内外学习割裂的情况。在此期间,教师要更重视分层意义,靶向补题。
“圆的面积”课后分层作业
(1)摸底补基
填空:小学数学中,用到了很多的数学思想,其中,圆面积公式的推导,就用到了____思想。小明把一个圆剪拼成一个近似的长方形后,周长比原来增加了10 厘米,这个圆的面积是____。
选择:一个钟表的时针长5 厘米,它一昼夜扫过的面积是多少平方厘米?列式是( )
A. 2×3.14×5 B. 5×3.14×52
C. 3.14×52D. 3.14×5
判断:一个圆的半径扩大3 倍,周长和面积也分别扩大3 倍。( )
解决问题:某小学校园建“开心农场”,用31.4 米的篱笆靠墙围出了两个完全相同的半圆形菜园,这两个半圆形菜园的占地面积是多少平方米?
(2)发展补强
解决问题:北京天坛公园中的圜丘是古时候举行冬至祭天大典的场所,造型为三层露天圆台,最下层直径56 米,最上层直径24 米。问:其上层坛半径与下层坛半径之比是多少?周长与面积之比又是多少?请列式求出最下层的坛的占地面积,说明最下层的坛的面积比最上层的多多少平方米。
开放探索:圆在生活中无处不在,矿泉水瓶盖是圆,小汽车轮胎是圆,钟表表盘是圆……找到一个你最感兴趣的圆,将它画下来,测量它的半径与直径,计算它的实际面积。同时,说明该圆形物品在生活中有哪些价值或作用。
(3)拔高补新
两个图形的重合度=重合面积÷(两个图形的面积和-重合面积)。例如,图5 中小圆的面积是4 平方厘米,大圆的面积是9 平方厘米,重合部分的面积是2平方厘米,重合度是。根据以上描述,解决下面的问题:一个正方形和一个圆摆在一起,有很多种摆法。图6 是乐乐想出来的三种摆法。其中,正方形边长均为4厘米,分别计算正方形与圆的重合度。假设还有两个半径分别为2 厘米、4 厘米的圆,它们之间最大的重合度又会是多少?

图5
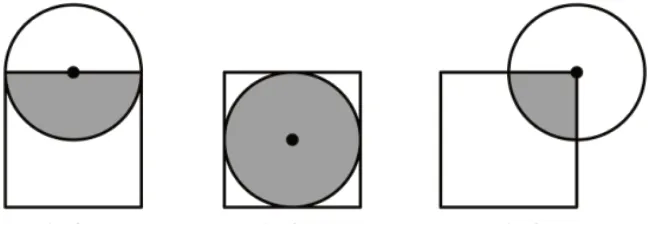
图6
针对知识掌握尚不扎实的基础层学生,教师可以设计“摸底补基”作业,使学生多角度回顾基础知识,进一步夯实基础;针对基础相对扎实、逻辑思维和运算能力亟待提高、更喜欢特色作业的发展层学生,设计“发展补难”作业,培养他们解决复杂问题的能力,同时,促进他们对课程内容的个性化探索;针对基础扎实、逻辑思维能力较强、具备一定复杂问题解答能力的学生,设计“拔高补新”作业,通过创新作业内容与形式,满足他们挑战自我的需要,提高他们的数学综合能力。
结 语
“双减”政策颁布后,教师要不断提高教研能力,增强“分层教学”“因材施教”意识,为学生提供恰当的教学与作业服务,帮助学生在最个性化的学习模式下实现最全面的发展。在契合学生“最近发展区”的分层作业中,教师更要引导学生由“我应该做作业”转变为“我要做作业”,在兼具基础性、创新性、开放性的题目中促进每一名学生的多元智能发展。
