基于函数值不动点逼近的四类改进迭代算法

郭 巧,杨 兵,吴昌广

(1.安徽职业技术学院计算机与信息技术学院,安徽 合肥 230611;2.安徽职业技术学院智能制造学院,安徽 合肥 230611;3.南京理工大学计算机学院,江苏 南京 210094)

0 引言

迭代法是非线性数值逼近求根的常用方法[1-4],主要有简单迭代法、Newton迭代法、弦割法,虽然这些方法运算简单,但都存在一定的局限性,如重根附近发散、迭代速率较低等.为避免诸如此类的问题,本文提出四类改进的求解非线性数值逼近的迭代法,并通过收敛性分析和数值实例验证,在保证收敛的前提下,其迭代速度明显优于简单迭代.

1 预备知识

定义1.1[5]将非线性方程f(x)=0等式两边同时加上x,得到

f(x)+x=x,

令h(x)=f(x)+x,将非线性方程求根等价变形为x=h(x).给定初始值x0,则有

(1)

其中,xn称为迭代序列,h(x)称为迭代函数,式(1)称为不动点迭代或简单迭代.

定义1.2 若对于任意x0∈[a,b],由式(1)产生的迭代序列满足:

则称迭代序列收敛.

2 四类改进迭代算法

2.1 点切式迭代

如图1所示,设非线性方程f(x)=0在点x0附近有一个单根,可将非线性方程等价变形为x=h(x),求非线性方程f(x)=0的根,即为求方程y1=x和y2=h(x)交点的横坐标.

过A0(x0,h(x0))作曲线y2=h(x)的切线交y1=x于B,切线方程为y-h(x0)=h′(x0)(x-x0).

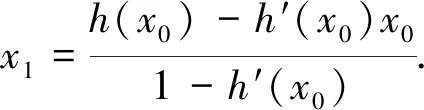
如此重复,得到点切式迭代公式:

(2)

图1 点切式迭代

2.2 切割式迭代

如图2所示,连接A0A1并延长交y1=x于点C,设C点横坐标为x1,则直线A0A1的方程为

将C(x1,x1)代入直线A0A1方程,得到

化简得到

如此重复,得到切割式迭代公式:

令

则

(3)

图2 切割式迭代

2.3 点点式迭代

如图3所示,在曲线y2=h(x)上取两点A0(x0,h(x0)),A1(x1,h(x1)),则直线A0A1的方程为

化简得到

因为直线A0A1与y1=x相交于点C(x2,y2),代入即得

化简得到

如此重复,则得点点式迭代公式:

(4)

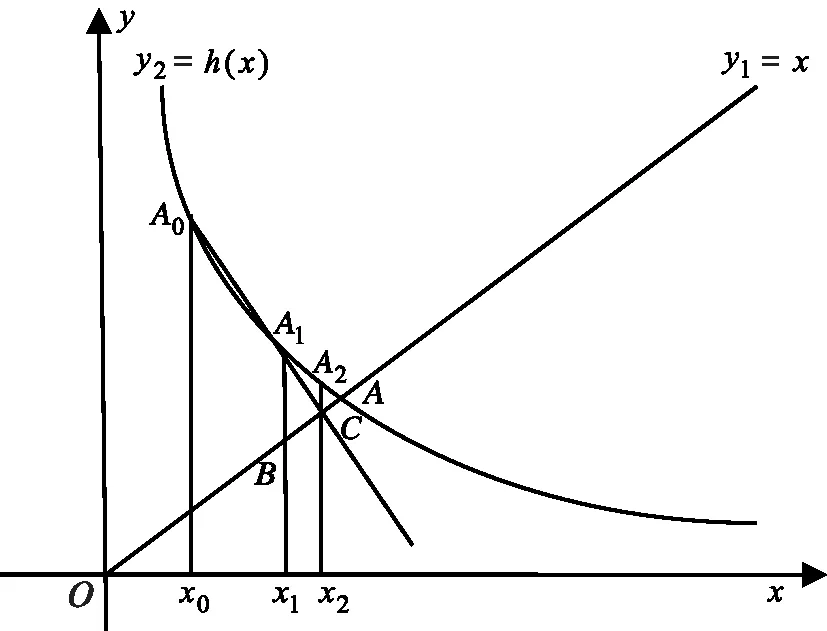
图3 点点式迭代

2.4 点斜式迭代

(5)

式(5)即为点斜式迭代.

图4 点斜式迭代

3 收敛性分析

本文研究求解非线性方程f(x)=0的变形x=h(x)在单根a处的迭代法.

定义3.1[6]设x*为h(x)的一个不动点,h′(x)在x*的某领域N(x*)连续且|h′(x*)|<1,则迭代法对任意x(0)∈N(x*)收敛.

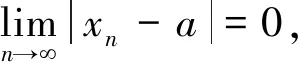
|xn+1-a|≤M|xn-a|p,

则称数列{xn}p阶收敛到a.

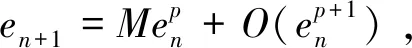
定理3.1 设x*为h(x)的一个不动点,如果xn→x*,则由公式(2)定义的迭代法二阶收敛,且误差方程为

其中,en=xn-x*,H(x*)为代替h(x*)的算法表达式.

证明 1)收敛性分析

当x=x*时,h(x*)=x,则H′(x*)=0,由定义3.1可知,迭代公式(2)收敛.

注 若对H′(x)继续求导,得到的H″(x*)≠0.

2)误差分析

对于公式(2),将H(x)在x*附近泰勒展开,得到

由xn+1=H(xn),x*=H(x*),en=xn-x*,H′(x*)=0,故上式变形为

故由公式(2)定义的迭代法二阶收敛.

定理3.2 设x*为h(x)的一个不动点,如果xn→x*,则由公式(3)定义的迭代法二阶收敛,且误差方程为

其中,en=xn-x*,H(x*)为代替h(x*)的算法表达式.

证明 1)收敛性分析

对于公式(3),令

对H(x)求导得到

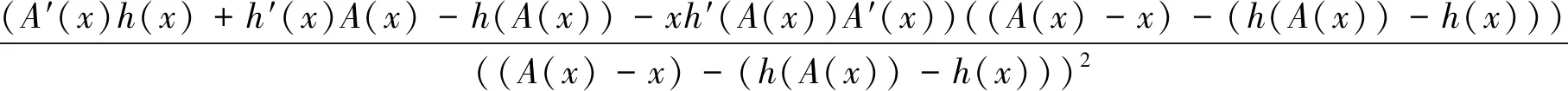
当x=x*时,h(x*)=x,由公式(2)可知,A′(x*)=0,由公式(1)可知,A(xn)→x*,则h(A(xn))→h(x*)→x*,代入上式,有H′(x*)=0,由定义3.1可知,迭代公式(3)收敛.

2)误差分析

对于公式(3),将H(x)在x*附近泰勒展开,则有

由xn+1=H(xn),x*=H(x*),en=xn-x*,H′(x*)=0,故上式变形为

故由公式(3)定义的迭代法二阶收敛.

定理3.3 设x*为h(x)的一个不动点,如果xn→x*,则由公式(4)定义的迭代法二阶收敛,且误差方程为

其中,en=xn-x*,H(x*)为代替h(x*)的算法表达式.公式(5)定义的迭代法线性收敛.

证明 1)收敛性分析

2)误差分析

对于公式(4),将H(x)在x*附近泰勒展开,有

由xn+1=H(xn),x*=H(x*),en=xn-x*,H′(x*)=0,故上式变形为

故由公式(4)定义的迭代法二阶收敛.

定理3.4 设x*为h(x)的一个不动点,如果xn→x*,则由公式(5)定义的迭代法线性收敛,且误差方程为

其中,en=xn-x*,H(x*)为代替h(x*)的算法表达式.

证明 1)收敛性分析

因为B为曲线h(x)在过横坐标为x0和x1两点所构成的直线的斜率,故B为常数,则H′(x*)≠0,且|H′(x*)|<1,由定义3.1可知,迭代公式(5)收敛.

2)误差分析

对于公式(5),将H(x)在x*附近泰勒展开,则有

由xn+1=H(xn),x*=H(x*),en=xn-x*,故上式变形为

故由公式(5)定义的迭代法线性收敛.

4 数值实例

例4.1 求非线性方程f(x)=e-x-x=0的根,取初值x0=0.5,令|xn-xn+1|≤10-4,通过简单迭代法的公式(1)、点切式迭代法的公式(2)、切割式迭代法的公式(3)、点点式迭代法的公式(4)、点斜式迭代法的公式(5)迭代算法,通过Matlab编程,计算结果见表1.

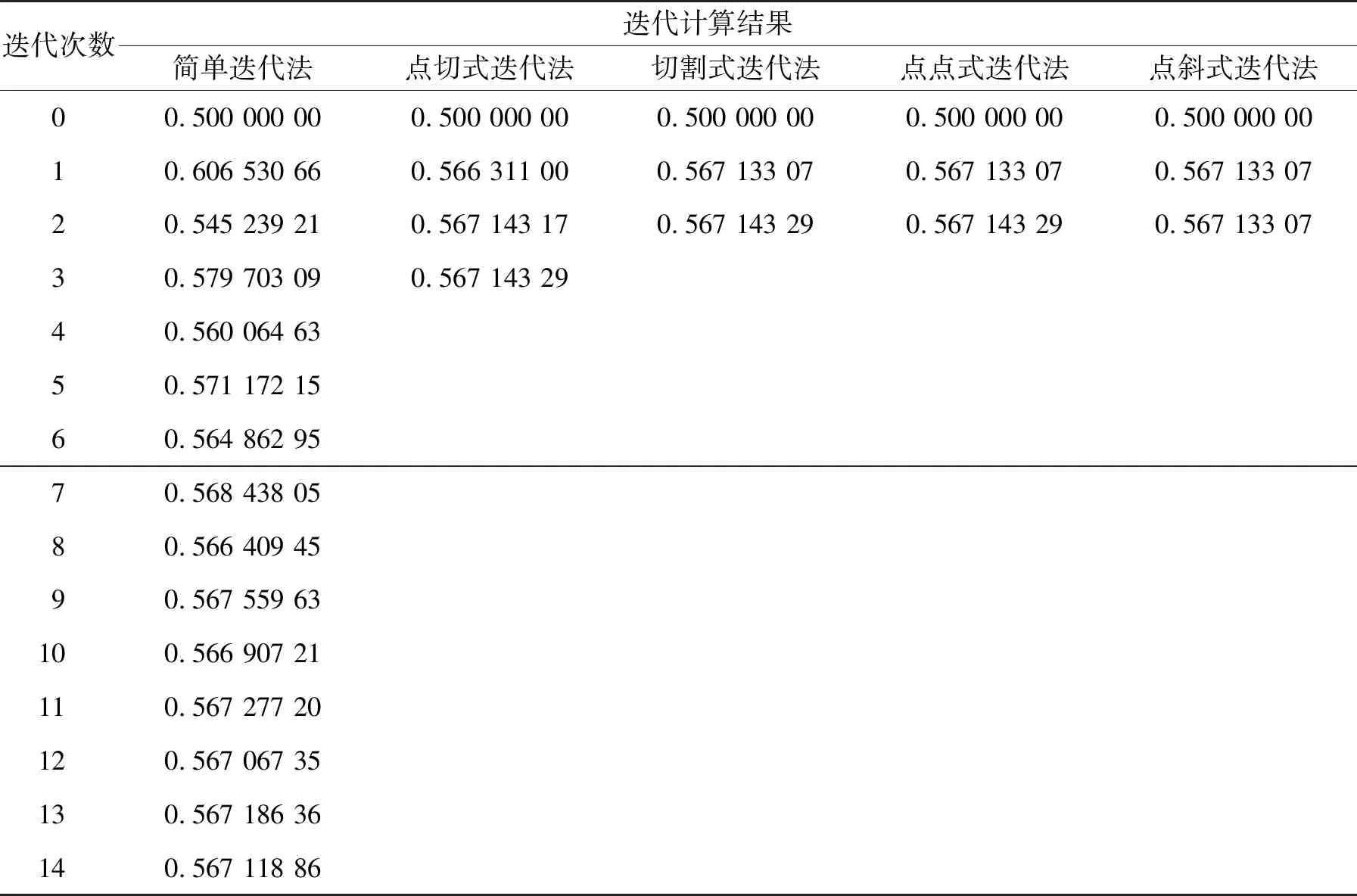
表1 例4.1计算结果

由表1可以看出,在初始值和精度要求相同的情况下,求解非线性方程近似根简单迭代法需要迭代14次才能达到精度要求,但是改进的点切式迭代法只需要迭代3次,切割式迭代法、点点式迭代法、点斜式迭代法分别只需要迭代2次,而点斜式迭代法在第一次迭代运算后就达到与第二次基本相同的迭代结果,改进的迭代算法收敛速度更快,并且能有效避免重根附近发散,该算法在机器人轨迹规划算法中具有较高的应用和推广潜力.