惯性β-Douglas-Rachford分裂算法收敛性分析

张家乐,欧阳薇

(云南师范大学数学学院,云南 昆明 650091)

0 引言

Douglas-Rachford分裂算法[1]常用于求解两个极大单调算子之和的零点集,即如下单调包含问题:

(1)

(2)

Douglas-Rachford算法最早由DOUGLAS和RACHFORD[6]于1956年提出.该方法最初用于求解热传导过程中产生的线性方程组的数值解,其弱收敛性和强收敛性已得到很好的证实[7-10].在强单调性、Lipschitz连续性和余强制性假设下,可以得到该算法及其对偶的线性收敛速度[11-17].

1979年,LIONS和MERCIER[1]推广了Douglas-Rachford方法,提出了经典Douglas-Rachford分裂算法,其格式如下:

1979年,GOL’SHTEIN和TRET’YAKOV[18]结合ROCKAFELLAR[19]提出的临近点算法,提出了广义的 Douglas-Rachford分裂算法,其格式如下:

其中,cn是松弛因子,cn∈(0,2).当cn∈(0,1)时,称cn为低松弛因子;当cn∈(1,2)时,称cn为超松弛因子.

2015年,BOT等[4]提出了惯性Douglas-Rachford分裂算法,其格式如下:

2019年,WANG等[20]基于经典Douglas-Rachford算法进行了细微改动,提出了含参数的Douglas-Rachford分裂算法,其格式如下:

2020年,陶永凯[21]在WANG等[20]提出的α-Douglas-Rachford分裂算法基础上进行了改进,提出了修正的αn-Douglas-Rachford分裂算法,其格式如下:

本文在BOT等[4]和陶永凯[21]提出的Douglas-Rachford分裂算法的基础上进行了相应修改,提出了一种新型的带参数的惯性Douglas-Rachford分裂算法,称为惯性β-Douglas-Rachford分裂算法,其格式如下:

(3)

1 符号说明

2 预备知识

则称映射A是μ-强单调的.当μ=0时,称A是单调的.

则称映射A是L-lipschitz连续的.当L=1时,称映射A是非扩张的;当L∈(0,1)时,称映射A是收缩的.

定义3 算子A的预解式和反射预解式分别定义如下:

JA∶=(A+Id)-1,RA∶=2JA-Id,

其中,Id表示恒等映射,即Id(x)=x.

注2 由算子A的β-增强算子的定义可知,A(β)是极大单调的.

(i)T是稳定非扩张的;

(ii)Id-T是稳定非扩张的;

(iii)2T-Id是非扩张的;

(iv)∀x,y∈D,‖Tx-Ty‖2≤〈x-y,Tx-Ty〉;

(v)∀x,y∈D,0≤〈Tx-Ty, (Id-T)x-(Id-T)y〉;

(vi)∀x,y∈D,∀α∈[0,1],‖Tx-Ty‖≤‖α(x-y)+(1-α)(Tx-Ty)‖.

‖(1-t)x+ty‖2=(1-t)‖x‖2+t‖y‖2-t(1-t)‖x-y‖2.

(4)

引理8[22]设(φn)n∈,(δn)n∈,(αn)n∈是[0,+∞)中的序列,使得对所有n≥1,有φn+1≤φn+αn(φn-φn-1)+δn成立,其中∞,并且存在一个实数α对所有n∈,有0≤αn≤α<1成立.则下列结论成立:

(ii)(xn)n∈的每个子序列的弱聚点都在C中.

则(xn)n∈弱收敛于C中的一个点.

zer(A+B)=JγB(FixRγARγB).

3 主要结论

下面建立逼近两个极大单调算子之和的零点集的惯性β-Douglas-Rachford分裂算法,并研究其收敛性质.在研究惯性β-Douglas-Rachford分裂算法的收敛性质之前,先证明两个辅助结果.

下面给出第一个辅助结果.

(i)T是非扩张的;

(ii)FixT≠∅,且JB(FixT)=zer(A+B+(2-2β)Id).

β‖JAx-JAy‖2≤‖JAx-JAy‖2≤〈JAx-JAy,x-y〉.

即

β‖JAx-JAy‖2≤〈JAx-JAy,x-y〉.

(5)

在(5)式两边同时乘4β,再加‖x-y‖2可得到

4β2‖JAx-JAy‖2+‖x-y‖2≤4β〈JAx-JAy,x-y〉+‖x-y‖2.

整理上式得到

4β2‖JAx-JAy‖2+‖x-y‖2-4β〈JAx-JAy,x-y〉≤‖x-y‖2.

根据完全平方公式,上式可变形为

‖2β(JAx-JAy)-(x-y)‖2≤‖x-y‖2,

即

‖(2βJA-Id)(x)-(2βJA-Id)(y)‖2≤‖x-y‖2.

(6)

由范数的非负性,(6)式可变形为

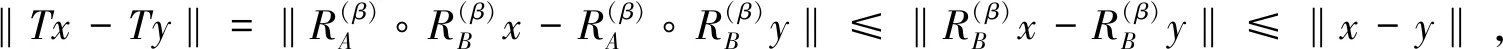
(ii)先证明JB(FixT)⊇zer(A+B+(2-2β)Id),即要证明:对于任意的x∈zer(A+B+(2-2β)Id),有x∈JB(FixT)成立.

由引理3可知,zer(A+B+(2-2β)Id)≠∅,则对任意的x∈zer(A+B+(2-2β)Id),有

0∈(A+B+(2-2β)Id)(x)=A(x)+B(x)+(2-2β)x.

(7)

因此,存在一个z∈B(x),使得

(2β-2)x-z∈A(x).

(8)

令z=y-x,则(8)式等价于

(2β-1)x-y∈A(x).

(9)

又因为x=JB(y),故(9)式等价于

2βJB(y)-y∈A∘JB(y)+JB(y)=(A+Id)∘JB(y).

(10)

(10)式意味着

JB(y)=JA(2βJB(y)-y).

(11)

则有

0=2βJA(2βJB(y)-y)-2βJB(y)⟺

y=2βJA(2βJB(y)-y)-(2βJB(y)-y)⟺

y=(2βJA-Id)∘(2βJB-Id)(y)⟺

(12)

因此,y是一个不动点,即FixT≠∅.由于y∈FixT,x=JB(y),故x∈JB(FixT).

下面证明JB(FixT)⊆zer(A+B+(2-2β)Id),即要证明:对任意的x∈JB(FixT),使得x∈zer(A+B+(2-2β)Id)成立.

因为x∈JB(FixT),所以存在y∈FixT使得x=JB(y).又因为(7)至(12)式是相互等价的,故有

x∈zer(A+B+(2-2β)Id).

综上可得,FixT≠∅,且JB(FixT)=zer(A+B+(2-2β)Id).

下面给出第二个辅助结果,即惯性K-M算法.值得注意的是,由于迭代格式中存在仿射组合,所以需将设置限制为仿射子空间上的非扩张算子,在考虑极大单调算子的反射预解式的组成时,这一假设是完全成立的.下面证明第二个辅助结果.

(13)

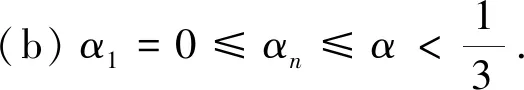
(ii)(xn)n∈弱收敛到FixT中的一点.

证明 (i)记wn∶=xn+αn(xn-xn-1),则对于任意n≥1,迭代方案(13)可变形为

(14)

对于任意n≥1,任取y∈FixT.由(4)式和T的非扩张性可得

(15)

再次使用(4)式有

‖wn-y‖2=(1+αn)‖xn-y‖2-αn‖xn-1-y‖2+αn(1+αn)‖xn-xn-1‖2.

(16)

因此,由(15)和(16)式可得

(17)

此外,由(14)式得到:

‖Twn-wn‖2=‖2(xn+1-xn)+2αn(xn-1-xn)‖2=

(18)

由(17)和(18)式可推出:

‖xn+1-y‖2-(1+αn)‖xn-y‖2+αn‖xn-1-y‖2≤(αn-1)‖xn+1-xn‖2+2αn‖xn-xn-1‖2.

(19)

接下来,使用文献[24]中的一些解题技巧来证明本文结论.

对于n∈,定义序列φn∶=‖xn-y‖2和ψn∶=φn-αnφn-1+2αn‖xn-xn-1‖2,其中ψ1=φ1≥0(因为α1=0).对于n∈,利用(αn)n≥0的单调性和φn≥0的事实,可得到

ψn+1-ψn≤φn+1-(1+αn)φn+αnφn-1+2αn+1‖xn+1-xn‖2-2αn‖xn-xn-1‖2.

由(19)式可得

ψn+1-ψn≤(αn-1)‖xn+1-xn‖2+2αn+1‖xn+1-xn‖2=

(αn-1+2αn+1)‖xn+1-xn‖2,∀n≥1.

(20)

由(αn)n≥0及α的选取可得

αn-1+2αn+1≤α-1+2α<0, ∀n≥1.

故序列(ψn)n≥0是非增的(严格减).

由ψn∶=φn-αnφn-1+2αn‖xn-xn-1‖2,序列(ψn)n≥0的非增性和(αn)n≥0的上界可得

-αφn-1≤φn-αφn-1≤ψn≤ψ1, ∀n≥1.

(21)

因为

φn≤αφn-1+ψ1≤α(αφn-2+ψ1)+ψ1=α2φn-2+ψ1+αψ1≤…≤αnφ0+ψ1+αψ1+…+αn-1ψ1,

故

由(20)和(21)式可得

设x是(xn)n∈的子序列(xnk)k∈的一个弱聚点,选取(wn)n∈的一个子列(wnk)k∈,则由(i)以及(wn)n∈的定义和(αn)n≥0的上界可得,当k→+∞时,wnk⇀x.此外,通过(14)式可得

‖Twn-wn‖=2‖xn+1-wn‖≤2(‖xn+1-xn‖+α‖xn-xn-1‖).

(22)

因此,由(i)可得,当k→+∞时,Twnk-wnk→0.将引理7应用到序列(wnk)k∈上,则有x∈FixT.

由于引理9的两个条件已得到验证,因此(xn)n∈弱收敛于FixT中的一点.

之所以要先证明两个辅助结果,是因为在接下来的证明中这两个辅助结果将产生重要作用.下面给出惯性β-Douglas-Rachford分裂算法的收敛性质并给出详细的证明.

(23)

其中,参数αn的选取满足定理1中的条件.

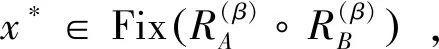
(ii)当n→+∞时,yn-zn→0;

(iii)序列(xn+1-wn)n∈→0;

(iv)(xn)n∈⇀x*;

证明 记wn=xn+αn(xn-xn-1),根据修正的反射预解式的定义,(23)式可变形为

(i)由定理1直接可得.

故由(22)式,当n→+∞时,有yn-zn→0.

(iii)由(23)式,序列(xn)n∈满足下式:

xn+1=wn+β(zn-yn)⟺xn+1-wn=β(zn-yn),

由(ii)可知,序列 (zn-yn)n∈强收敛于0,所以序列(xn+1-wn)n∈强收敛于0.

(iv)由命题1和定理1可得,序列(xn)n∈弱收敛于中的一点x*,即 (xn)n∈⇀x*.

(v)由命题1可知,FixT≠∅,且JB(FixT)=zer(A+B+(2-2β)Id).应用定理1,则存在x*∈FixT,使得JBx*∈zer(A+B+(2-2β)Id).

又由命题1可知,x∈zer(A+B+(2-2β)Id),即

0∈A(x)+B(x)+(2-2β)x.

(24)

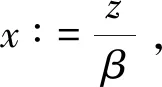
由定义6,有

0∈A(β)(z)+B(β)(z).

(25)

则由(25)式可得z∈zer(A(β)+B(β)),故zer(A(β)+B(β))≠∅.

又因为A(β),B(β)都是单调算子,故由引理10可得

JB(β)(x*)∈zer(A(β)+B(β)).

由引理5可得

JB(β)(x*)=βJB(x*).

进一步,由引理4可得

由于极大单调算子的预解式是单值映射,所以,

由此定理2得证.

4 结论与展望

在接下来的工作中,将继续围绕惯性β-Douglas-Rachford分裂算法等相关问题进行研究,如将其用于求解变分不等式、原始对偶问题等.