二阶潜增长模型标度方法及其可比的一阶潜增长模型*

温忠麟 王一帆 杜铭诗 俞雅慧 张愉蕙 金童林

二阶潜增长模型标度方法及其可比的一阶潜增长模型*

温忠麟1王一帆1杜铭诗1俞雅慧1张愉蕙1金童林2

(1华南师范大学心理应用研究中心/心理学院, 广州 510631) (2内蒙古师范大学心理学院, 呼和浩特 010022)

潜增长模型(LGM)是分析纵向数据的一种强有力工具, 在心理学和其他社会科学研究领域受到重视。多指标测量的变量, 既可以用合成分数建立单变量LGM(一阶LGM), 也可以用指标建立潜变量LGM(二阶LGM)。简述了二阶LGM标度方法(包括尺度指标法和效应编码), 提出了有可操作性的潜变量标准化标度方法和合成分数的一阶LGM标准化模型。系统总结了二阶LGM标度方法及其可比的一阶LGM建模, 并用多指标变量的实测数据进行示例。推荐使用效应编码法对二阶LGM进行标度和标准化。

潜增长模型, 合成分数, 标度方法, 尺度指标, 效应编码, 潜变量标准化

为了模型识别(identification), 验证性因子分析(CFA)的一项基础工作是因子标度(scaling), 即为因子设定测量单位和测量原点(侯杰泰等, 2004)。先说设定测量单位, 通常的标度方法(scaling method, 也称为识别方法)是使用固定负荷法或者固定方差法指定测量单位。固定负荷法是对每个因子, 都将其中一个指标的负荷(loading)固定为一个常数, 相应的指标称为尺度指标(scaled-indicator或者mar­ker-variable)。最方便的是固定负荷为1, 此时因子的测量单位与尺度指标的测量单位相同; 固定方差法是将每个因子的方差固定为一个常数, 最方便的是固定方差为1。再说设定测量原点, 对于无均值结构的模型, 其实是将因子均值和指标的截距(intercept)都固定为0; 对于有均值结构的模型(Mplus软件默认),有两种标度方法：一种是将因子的均值固定为0, 另一种是将尺度指标的截距固定为0。

潜增长模型(latent growth model, LGM)是分析纵向数据的一种强有力工具, 在心理学和其他社会科学研究领域受到重视(例如, Jeon & Kim, 2021; Yang et al., 2021; 也见本文讨论部分)。LGM是一种特殊的因子模型, 它的标度方法有什么特殊性？用潜变量(latent variable)建立的LGM应当如何标度, 才能与用显变量建立的LGM有可比性？这些是本文要研究的主要问题。本文先介绍单变量LGM (一阶LGM)和潜变量LGM (二阶LGM); 然后简述二阶LGM标度方法, 提出有可操作性的潜变量标准化标度方法, 并在此基础上系统总结二阶LGM标度方法及其可比的一阶LGM建模; 接着使用一个多指标变量的实测数据, 对所论的标度方法建模并比较一阶和二阶LGM的参数估计结果; 最后对二阶LGM标度和模型标准化方法做出推荐。

1 潜增长模型

1.1 单变量潜增长模型

虽然有一些文献从潜在状态−特质理论(latent state-trait theory)出发导出LGM方程(例如, Mayer et al., 2012; Geiser et al., 2013), 但更直接、更容易理解的还是从时间为自变量的普通回归方程导出(例见：李丽霞等, 2012)。

每个被试都有相应的α和β, 但不能直接观测得到, 属于潜变量(即因子)。熟悉因子分析的读者, 不难将方程(1)理解为有两个因子(和, 分别称为截距因子和斜率因子)、个指标(1,2, …,X)的测量方程。为了简便起见, 下面以= 4为例, 测量方程如下(按通常因子模型的写法忽略被试下标)：

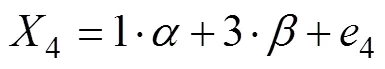
图1 一阶LGM的例子

注：三角形出发的路径系数是与均值结构有关的参数。

方程(2)两边求均值

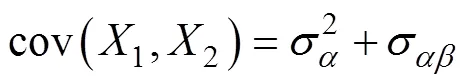
求解方程组(8)～(10)得到

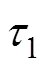
虽然本节讨论的是测量间隔相等的线性增长模型, 但不难推广到一般的情形。当随时间变化是非线性增长时, 可以在回归方程中增加(− 1)的二次甚至更高次的项, 变成多项式回归, 但多项式的次数必须少于追踪测量次数。例如, 模型包含二次增长, 则相应的LGM在截距、斜率(一次)因子之外, 需要增加一个二次因子, 相应地, 负荷矩阵增加一列, 由(− 1)的平方产生, 依次为0, 1, 4, 9。包含更高次多项式的LGM依次类推。当时间间隔不相等时, 将第一个间隔设定为1, 后面的间隔根据其与第一个间隔的长短比例进行调整,可能不是整数。例如, 4个测量时间点的间隔依次为2个月、3个月、2个月, 则1, 2, 3.5, 4.5, 即增加1表示间隔2个月。

1.2 二阶潜增长模型

在心理、行为、管理、教育等研究领域, 变量往往不是显变量, 而是需要一组题目去间接测量的潜变量(记为η)。这时既可以使用题目的合成分数(composite score)去建立单变量LGM, 也可以使用潜变量(以题目为指标)去建立二阶LGM (second-order latent growth model)。

直接使用(题目)指标建立潜变量测量模型, 然后使用每个时间点的潜变量(也就是通常CFA中的因子)建立LGM, 就得到McArdle (1988)所说的因子曲线模型(the curve-of-factors model)。这种二阶LGM, 其实是一种特殊的二阶因子模型, 其中一阶因子是一组题目测量的潜变量, 二阶因子才是截距因子和斜率因子。

二阶LGM中的二阶因子测量方程为

图2 二阶LGM的例子

注：三角形出发的路径系数是与均值结构有关的参数。假设纵向测量强不变性成立, 即指标负荷和截距不随时间变化。

由(17)和(18)可知, 与方程(6)和(7)相应的是

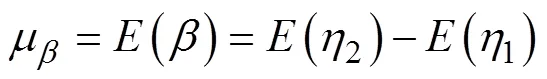
2 二阶潜增长模型的标度方法

二阶LGM的一阶因子(即潜变量)和二阶因子(即截距因子和斜率因子)都需要标度。二阶因子的标度方法和单变量LGM的一样, 这里重点讨论二阶LGM的一阶因子的标度方法。Yang等人(2021)介绍了三种标度方法, 包括尺度指标法、效应编码法和潜变量标准化法。无论哪种方法, 都有一个等式限制负荷(设定潜变量测量单位)、一个等式限制截距(设定潜变量测量原点)。下面我们重新演绎, 简化了很多。尤其是对原来缺乏可操作性的潜变量标准化法, 提出了简单而有可操作性的新方法。

2.1 尺度指标法

再由方程(6’)、(7’)结合(21)可得

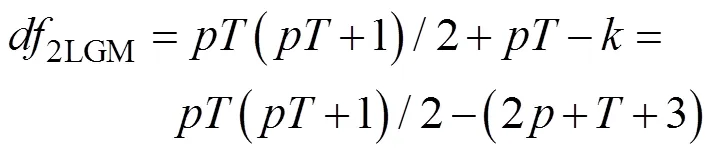
后面介绍的两种潜变量标度方法得到的自由度与尺度指标法得到的一样。如果所写的程序运行结果得到的自由度与理论计算的不同, 说明程序没有写对, 很多时候都是潜变量标度有误。但要注意, 如果不是线性LGM, 需要估计的参数一般会更多, 自由度计算公式需要相应改变。

2.2 效应编码法

效应编码法(effect-coding method)是将各时间点的一阶因子测量方程的全部截距之和限制为0, 同时将全部负荷之和限制为一个常数(Little et al., 2006; Yang et al., 2021), 下面讨论文献上最常见的两种做法。

由方程(14)～(16)可知, 对任一时间点, 3个指标之和为

再由方程(6’)、(7’)结合(26)可得

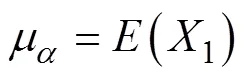
方程(27)、(28)分别与方程(6)、(7)形式一模一样。同理还可推出(11)～(13)一样的方程组。这说明, 二阶LGM中限制截距之和为0、负荷之和为1, 得到的5个参数方程与使用合成分数(总和)建立单变量LGM得到的一样(但还有其他不一样的方程, 因为LGM是超识别的, 方程个数多于参数个数), 两者有接近的参数估计。

得到与(26)一模一样的方程。这说明, 二阶LGM限制截距之和为0、负荷之和为指标个数, 得到的参数方程中有5个与使用合成分数(平均分)建立单变量LGM得到的一样(但还有其他不一样的方程), 两者有接近的参数估计。

正如使用总分与使用平均分做单变量LGM得到的参数估计很不相同, 限制负荷之和等于1与等于指标数, 得到的二阶LGM参数估计也很不相同, 两者的均值参数有倍数(指标个数)关系, 方差也有倍数(指标个数的平方)关系。

2.3 潜变量标准化法

前面介绍的两种标度方法可能会得到很不同的二阶LGM结果, 不仅不同标度方法得到的结果没有可比性, 同一种标度方法下选用不同限制等式得到的结果也没有可比性。Yang等人(2021)借鉴前人的做法(Ferrer et al., 2008; Grimm et al., 2017), 将某个时间点的潜变量进行标准化, 变成均值为0、方差为1的标准化变量。这个时间点称为参照点, 如果没有特别说明, 默认选择第一个时间点, 相当于将初始水平设定为0, 初始方差设定为1, 并作为比较的基准, 而后面时间点潜变量在纵向测量强不变性限制下相应变化均值(一般不是0)和标准差(一般不是1)。

Yang等人(2021)提出的基于尺度指标法的潜变量标准化法(latent-standardization method)如下：

2)将尺度指标的负荷固定为尺度指标的方差乘以其信度后开方, 即

下面解释一下其做法, 以理解这种做法的本质。由方程(14)有

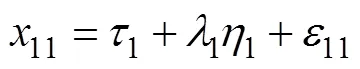
这样, 我们可以提出既简单又有可操作性的潜变量标准化法(两阶段建模)。基于尺度指标法的潜变量标准化法如下：

基于效应编码法的潜变量标准化法如下：

第一阶段与基于尺度指标法的潜变量标准化法一样;

第二阶段：建立二阶LGM, 将各指标的截距之和限制为第一时间点各指标的样本均值之和, 即

3 一阶和二阶潜增长模型的可比性

对于多指标测量的变量, 既可以使用合成分数建立一阶LGM, 也可以使用潜变量建立二阶LGM。讨论一阶和二阶LGM的可比性, 不仅在需要比较两者的时候能找对比较的对象, 而且可以更好地理解二阶LGM标度方法。

3.1 基于尺度指标法的比较

这样说来, 最常使用的尺度指标法并不理想, 一方面, 使用不同指标做尺度指标会得到可能很不同的结果, 就如使用不同指标建立的单变量LGM会有很不同的结果一样。另一方面, 使用尺度指标法, 至少在初始水平和斜率的均值参数估计上主要依赖尺度指标, 从而与效应编码法的结果可能会有较大出入。

3.2 基于效应编码法的比较

由2.2节可知, 二阶LGM使用限制截距之和为0、负荷之和为1的效应编码法, 与使用合成总分建立的单变量LGM有可比性, 两者可以得到主要LGM参数的5对一样的方程。但两种模型都属于超识别模型(侯杰泰等, 2004), 关于参数的方程多于参数个数, 两种模型还有其他不一样的方程, 因而两种模型的参数估计只是接近而不是完全等同。和一般结构方程模型一样, 两种模型参数接近的程度与合成分数的信度有关(温忠麟等, 2022)。

二阶LGM使用限制截距之和为0、负荷之和为指标个数的效应编码法, 与使用平均分合成分数建立的单变量LGM有可比性, 两者可以得到主要LGM参数的5对一样的方程。两者关系的讨论同上。

3.3 基于潜变量标准化法的比较

3.4 小结

根据上面的讨论, 可以将一阶和二阶LGM的比较结果列成表1。对于多指标测量的变量, 要建立一阶LGM的时候, 几乎都会使用合成分数, 而罕有使用单指标建模; 但二阶LGM常用的潜变量标度方法却是尺度指标法(Yang et al., 2021)。例如, Leite (2007)通过模拟的方法比较一阶LGM和二阶LGM对参数的估计情况, 一阶LGM使用平均分合成分数建模, 而二阶LGM使用尺度指标法(并与产生数据的真模型一样), 两者缺乏可比性, 所以该文比较的结果没有意义。为了与使用平均分合成分数的一阶LGM比较, 二阶LGM应当使用平均分的效应编码法(并与产生数据的真模型一样)。

4 实际数据展示

这里用一个实例比较表1中各种标度方法的二阶LGM及相应的一阶LGM, 看看5个LGM参数估计结果在不同标度方法上的差异, 以及一阶和二阶LGM可比性的情况。变量是道德推脱中的“责任转移”维度。这里主要是方法展示, 不过多涉及与方法无关的具体细节。

采用王兴超和杨继平(2010)修订的《中文版道德推脱问卷》。该问卷共26个题目, 采用１(完全不同意)～5(完全同意)五点计分, 共有8个维度, 选取其中的“责任转移”维度, 该维度有3个题目(指标)。被试是高校本科生, 追踪测量4次, 间隔1个月, 共有1209个被试有完整的数据。4次测量的α系数在0.72～0.87之间。更多信息可参见金童林等(2023)。采用Mplus 8.3做CFA(包括一阶和二阶LGM)。

先做纵向测量不变性检验, 因为被试人数多, 不适合使用嵌套模型的卡方差异检验。改用拟合指数CFI和RMSEA的差异检验。对于人数超过300、各组人数相当的多组测量不变性检验, 如果加上限制条件的模型的CFI降低不超过0.01、RMSEA提高不超过0.015, 则选择比较简单的模型, 即不变性成立(Chen, 2007)。基准模型(没有限制条件)、弱不变性模型(限制各时间点的负荷相等)和强不变性模型(限制各时间点的负荷相等、截距相等)的主要拟合指数见表2。强不变性模型与基准模型相比, ∆CFI = −0.009 (CFI降低不超过0.01), ∆RMSEA = −0.005 (RMSEA不升反降), 所以纵向测量强不变性成立。

表1 二阶LGM标度方法与可比的一阶LGM建模

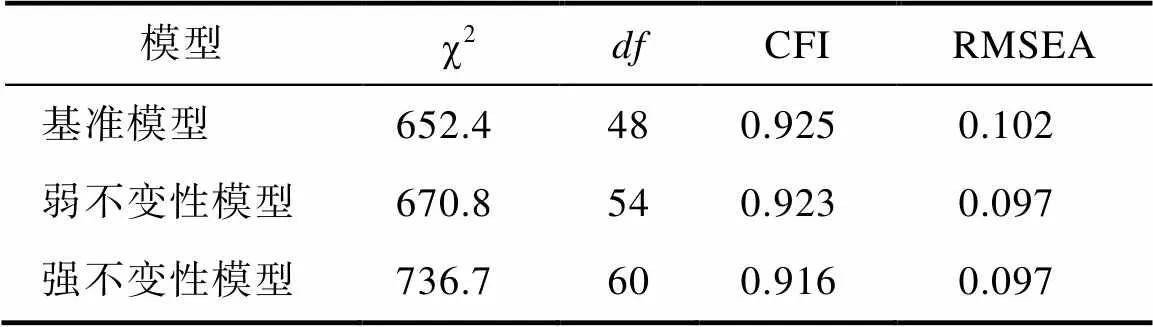
表2 纵向测量不变性检验

注：= degrees of freedom, CFI = comparative fit index, RMSEA = root mean square error of approximation.

第一时间点潜变量均值为0、方差为1时(Mplus程序见附录1), 3个指标的负荷分别为：0.743, 0.679, 0.459, 这些数值在潜变量标准化时需要用到(见2.3节); 相应的单指标信度分别为：0.67, 0.65, 0.25, 可以通过信度高低检视尺度指标法的效果。

不同标度方法的二阶LGM及相应的一阶LGM的5个参数估计见表3, 为了方便比较, 还加上了截距因子与斜率因子的相关系数, 它不是LGM的参数, 可以通过方差和协方差计算得到。不同标度方法的二阶LGM参数估计结果可能会很不相同, 但模型的自由度都是65 (可以用公式23计算), 而且拟合指数也相同：χ2= 754.52, CFI = 0.914, TLI = 0.913, RMSEA = 0.094, SRMR = 0.067。

对于尺度指标法, 一阶和二阶LGM的参数估计结果有明显差异(通常最感兴趣的斜率因子均值差异超过10%), 尤其是信度比较低的指标3作为尺度指标的时候。二阶LGM考虑了潜变量的测量误差, 虽然主要依赖尺度指标, 但还是使用全部指标的信息, 而一阶LGM仅仅使用了尺度指标, 而且没有考虑测量误差, 当信度低(误差方差大)的时候, 其估计结果与二阶LGM的差异大是意料中的事情。此外, 无论一阶还是二阶LGM, 使用不同的尺度指标的结果可比性低。

对于效应编码法(二阶LGM的Mplus程序见附录2), 无论合成总分还是合成均分建模, 一阶和二阶LGM的参数估计差异都不超过10%, 两种模型都使用了全部指标信息, 差异在于是否考虑了测量误差, 即潜变量建模与显变量建模的差异。此外, 无论一阶还是二阶LGM, 合成总分与合成均分建模尺度相差很大, 但两者的增长参数符合理论预期的倍数关系。

当第一时间点的潜变量标准化时, 可以得到LGM的标准化估计。理论上说, 截距因子均值的标准化估计近似于0。实际结果是, 一阶LGM的截距因子均值近似于0且不显著; 三种二阶LGM标准化估计, 除了截距因子的均值外完全一致, 但截距因子均值有明显差异, 两种尺度指标法的结果与0有显著差异, 而效应编码法的结果近似于0且不显著, 说明二阶LGM标准化应当使用效应编码法比较好。此外, 不出所料, 无论一阶还是二阶LGM,合成总分和合成均分建模有完全相同的标准化估计。

表3 不同标度方法的二阶LGM及相应的一阶LGM比较结果

注：没有注明一阶便是二阶。除了带下划线的三个截距因子均值(标准化估计)外, 所有参数在0.01水平上都显著。不出所料, 合成总分和合成均分的一阶LGM有完全相同的标准化估计。基于合成总分和合成均分的二阶LGM也有完全相同的标准化估计, 没有分别列出, 统称为基于合成分数的标准化估计。

5 讨论

LGM可以同时分析个体随时间的发展变化和个体间的发展差异(Jeon, & Kim, 2021; Laird & Ware, 1982), 在追踪研究中受到广泛应用。一阶LGM使用单变量建模, 容易理解、操作简单。我们以中国知网(https://www.cnki.net)全文数据库作为数据源, 不限出版年与学科, 检索所有涉及潜增长模型的中文文献。主题或摘要或关键词包括：“潜增长”、“潜增长模型”、“潜增长曲线模型”、“因子曲线模型”、“潜在增长”、“潜在增长模型”、“潜在增长曲线模型”、“LGM”。使用了LGM的应用文章210篇(其中心理学119篇), 仅有5篇使用了二阶LGM (其中只有1篇心理学论文)。英文期刊上二阶LGM的使用也很少, Yang等人(2021)检索了4个心理学期刊上从创刊至2019年11月的全部文章, 共有300篇文章应用了LGM, 只有11篇使用了二阶LGM。无论中文还是英文文章, 只有少数报告了使用尺度指标法, 多数没有报告标度方法。绝大多数文章使用Mplus进行二阶LGM分析, 可以推测是使用了默认的尺度指标法。

单变量一阶LGM的不足之处是, 忽略了测量误差、通常不去检验纵向测量不变性。对于多指标测量的变量, 使用合成分数做一阶LGM的优点是简单易理解, 前提条件也是满足纵向测量不变性并且是严格不变性(即各指标的负荷、截距和误差方差都是跨时间不变的)。如果严格不变性不成立, 使用合成分数做单变量LGM会引起参数估计偏差, 因为这种LGM不能区分潜变量的真实纵向变化与测量上的变化(Leite, 2007; Sayer & Cumsille, 2001)。二阶LGM可以弥补一阶LGM的不足, Geiser等人(2013)总结了二阶LGM的优势：可以将测量误差分离出来; 可以检验纵向测量不变性(其实这个检验可以独立于LGM进行); 在检验发展变化的个体差异方面有较高的统计检验力; 可以分离题目指标的方法效应。

正确使用二阶LGM的一个前提是理解模型识别和因子的标度方法, 以及二阶与一阶的联系。本文基于Yang等人(2021)的标度方法分类, 简化了尺度指标法和效应编码法的推演方式, 提出了简单而有可操作性的二阶LGM标准化估计方法, 系统总结了二阶LGM标度方法及其可比的一阶LGM建模。

除非对某个指标情有独钟而且该指标信度很高, 否则不要使用尺度指标法, 因为这样标度的二阶LGM结果只与尺度指标建立的单变量LGM有可比性, 不同的尺度指标可能导致很不同的结果。效应编码法比较好, 同时使用了全部指标的信息进行标度, 结果与使用合成分数的单变量LGM有可比性。可以根据研究目的决定使用总分还是平均分的效应编码法, 通常使用平均分的比较好, 不受指标数量的影响。

和其他结构方程模型一样, 标准化估计可以帮助解释结果, 比较不同研究之间的效应大小。虽然理论上说基于不同标度方法得到的标准化估计有唯一性, 但由于潜变量标准化的间接性, 标准化后的参照点潜变量只是近似的标准化变量, 因而参数估计可能与标准化方法有关。基于效应编码法的标准化明显好于基于尺度指标法的标准化。

由于不同标度方法的LGM结果很不相同, 需要明确说明所用的标度方法, 并对估计结果做出相应的解释。一般情况下推荐使用效应编码法对二阶LGM进行标度和标准化。这时, 有可比性的一阶LGM是使用合成分数的单变量LGM。对一阶LGM而言, 合成总分和合成均分得到的标准化结果相同; 对二阶LGM而言, 合成总分和合成均分对应的效应编码法的标准化结果也相同。

表3列出的三种二阶LGM标准化估计, 除了截距因子均值外, 其他4个LGM参数估计都完全一致。这是巧合还是必然, 需要进一步研究。还有, 二阶LGM与一阶LGM的关系是潜变量建模与显变量建模的关系, 但比回归模型中的这种关系要复杂, 两者的关系如何受到测量信度的影响, 有待进一步研究。

Chen, F. F. (2007). Sensitivity of goodness of fit indexes to lack of measurement invariance.(3), 464–504.

Chou, C. P., Bentler, P. M., Pentz, M. A. (1998). Comparisons of two statistical approaches to study growth curves: The multilevel model and the latent curve analysis.(3), 247–266.

Ferrer, E., Balluerka, N., & Widaman, K. F. (2008). Factorial invariance and the specification of second-order latent growthmodels.(1), 22–36.

Geiser, C., Keller, B., & Lockhart G. (2013). First versus second order latent growth curve models: Some insights from latent state-trait theory.(3), 479–503.

Grimm, K. J., Ram, N., & Estabrook, R. (2017).. Guilford Press.

Hau K. T., Wen Z., & Cheng Z. (2004).Beijing: Educational Science Publishing House.

[侯杰泰, 温忠麟, 成子娟. (2004).. 北京：教育科学出版社.]

Jeon, M. J., & Kim, S. Y. (2021). Performance of second-order latent growth model under partial longitudinal measurement invariance: A comparison of two scaling approaches.,(2), 261–277.

Jin, T., Xu, M., & Wu, Y. T. N. (2023). The changes of moral disengagement in Chinese college students: Evidence from cross-temporal meta-analysis and longitudinal study.,(1), 110–116.

[金童林, 徐明爽, 乌云特娜. (2023). 中国大学生道德推脱的变迁：横断历史研究与追踪研究的证据.,(1), 110–116. ]

Kim, E. S., & Willson, V. L. (2014). Testing measurement invariance across groups in longitudinal data: Multigroup second-order latent growth model.,(4), 566–576.

Laird, N. M., & Ware, J. H. (1982). Random-effects models for longitudinal data.(4), 963–974.

Leite W. L. (2007). A comparison of latent growth models for constructs measured by multiple items.,(4), 581–610.

Li, L., Gao, Y., Zhang M., & Zhang, Y. (2012). The latent variable growth curve model and its applications.,(5), 713–716.

[李丽霞, 郜艳晖, 张敏, 张岩波. (2012). 潜变量增长曲线模型及其应用.,(5), 713–716. ]

Li, L., Zhou, S., Zhang, M., Zhang, Y., & Gao, Y. (2014). Comparisons of two statistical approaches in studying the longitudinal data: The multilevel model and the latent growth curve model.,(6), 741–744.

[李丽霞, 周舒冬, 张敏, 张岩波, 郜艳晖. (2014). 多水平模型和潜变量增长曲线模型在纵向数据分析中的应用及比较.,(6), 741–744. ]

Little, T. D., Slegers, D. W., & Card, N. A. (2006). A non-arbitrary method of identifying and scaling latent variables in SEM and MACS models.,(1), 59–72.

Mayer, A., Steyer, R., & Mueller, H. (2012). A general approach to defining latent growth components.(4), 513–533.

McArdle, J. J. (1988). Dynamic but structural equation modeling of repeated measures data. In J. R. Nesselroade & R. B. Cattell (Eds.),(2nd ed., pp. 561–614). New York: Plenum.

Sayer, A. G., & Cumsille, P. E. (2001). Second-order latent growth models. In L. M. Collins & A. G. Sayer (Eds.),(pp. 179–200). Washington, DC: American Psychological Association.

Wang, X., & Yang, J. (2010). Reliability and validity of moral disengagement scale in Chinese students.,(2), 177–179.

[王兴超, 杨继平. (2010). 中文版道德推脱问卷的信效度研究.,(2), 177–179. ]

Wen, Z., Chen, H., Fang, J., Ye, B., & Cai, B. (2022). Research on test reliability in China’s mainland from 2001 to 2020.,(8), 1682–1691.

[温忠麟, 陈虹熹, 方杰, 叶宝娟, 蔡保贞. (2022). 新世纪20年国内测验信度研究.(8), 1682–1691.]

Wen, Z., & Liu, H. (2020).Beijing: Educational Science Publishing House.

[温忠麟, 刘红云. (2020).北京: 教育科学出版社.]

Wen, Z., & Ye, B. (2011). Evaluating test reliability: From coefficient alpha to internal consistency reliability.(7), 821–829.

[温忠麟, 叶宝娟. (2011). 测验信度估计：从α系数到内部一致性信度.,(7), 821–829.]

Wu, Y., & Wen, Z. (2011). Item parceling strategies in structural equation modelling.,(12), 1859–1867.

[吴艳, 温忠麟. (2011). 结构方程建模中的题目打包策略.,(12), 1859–1867.]

Yang, Y., Luo, Y., & Zhang, Q. (2021). A cautionary note on identification and scaling issues in second-order latent growth models.,(2), 302–313.

TITLE: CFA with strong MI (standardized f1)

DATA: FILE IS p1.csv;

VARIABLE: NAMES ARE x11-x13 x21-x23 x31-x33 x41-x43;

MODEL:

f1 BY x11-x13* (L1-L3);

f2 BY x21-x23* (L1-L3);

f3 BY x31-x33* (L1-L3);

f4 BY x41-x43* (L1-L3);

!设定负荷自由估计, 跨时间不变;

[x11 x21 x31 x41] (tau1);

[x12 x22 x32 x42] (tau2);

[x13 x23 x33 x43] (tau3);

!设定截距跨时间不变;

f1@1; !固定f1的方差为1;

[f1@0]; !固定f1的均值为0, Mplus默认;

[f2-f4*]; !f2-f4的均值自由估计;

!注释：结果用于二阶潜增长模型的潜变量标准化法(见附录2);

TITLE: Second-order Latent Growth Models;

DATA: FILE IS p2.csv;

VARIABLE: NAMES ARE x11-x13 x21-x23 x31-x33 x41-x X1mean-X4mean Z1-Z4;

!Z1为X1mean的Z分数, Z2-Z4为X2mean-X4mean的线性变换;

USEVARIABLES are x11-x13 x21-x23 x31-x33 x41-x43;

MODEL:

f1 BY x11-x13* (L1-L3);

f2 BY x21-x23* (L1-L3);

f3 BY x31-x33* (L1-L3);

f4 BY x41-x43* (L1-L3);

!设定负荷自由估计, 跨时间不变;

[x11 x21 x31 x41] (tau1);

[x12 x22 x32 x42] (tau2);

[x13 x23 x33 x43] (tau3);

!设定截距跨时间不变;

i s | f1@0 f2@1 f3@2 f4@3; !定义潜变量LGM, i为截距因子α, s为斜率因子β;

[i*]; !截距因子均值自由估计;

i(ivar); s(svar); i with s (cov);

!为计算相关系数, 储存方差/协方差估计值;

MODEL CONSTRAINT:

NEW (rel); !定义新变量;

rel=cov/sqrt(ivar*svar); !计算截距因子与斜率因子的相关系数;

0 = L1+L2+L3-3; !限制负荷之和等于指标个数(或者1), 对应于合成均分(总分)建模;

0 = tau1+tau2+tau3; !限制截距之和等于0;

!注释：如果要得到标准化估计, 最后两行限制应当换成：

0 = L1+L2+L3-1.881; !1.881是第一阶段做CFA (附录1)得到的负荷之和;

0 = tau1+tau2+tau3-5.685; !5.685是指标在第一时间点的样本均值之和;

Scaling methods of second-order latent growth models and their comparable first-order latent growth models

WEN Zhonglin1, WANG Yifan1, DU Mingshi1, YU Yahui1, ZHANG Yuhui1, JIN Tonglin2

(1Center for Studies of Psychological Application & School of Psychology, South China Normal University, Guangzhou 510631, China) (2College of Psychology, Inner Mongolia Normal University, Hohhot 010022, China)

Latent growth models (LGMs) are a powerful tool for analyzing longitudinal data, and have attracted the attention of scholars in psychology and other social science disciplines. For a latent variable measured by multiple indicators, we can establish both a univariate LGM (also called first-order LGM) based on composite scores and a latent variable LGM (also called second-order LGM) based on indicators. The two model types are special cases of the first-order and second-order factor models respectively. In either case, we need to scale the factors, that is, to specify their origin and unit. Under the condition of strong measurement invariance across time, the estimation of growth parameters in second-order LGMs depends on the scaling method of factors/latent variables. There are three scaling methods: the scaled-indicator method (also called the marker-variable identification method), the effect-coding method (also called the effect-coding identification method), and the latent-standardization method.

The existing latent-standardization method depends on the reliability of the scaled-indicator or the composite scores at the first time point. In this paper, we propose an operable latent-standardization method with two steps. In the first step, a CFA with strong measurement invariance is conducted by fixing the mean and variance of the latent variable at the first time point to 0 and 1 respectively. In the second step, estimated loadings in the first step are employed to establish the second-order LGM. If the standardization is based on the scaled-indicator method, the loading of the scaled-indicator is fixed to that obtained in the first step, and the intercept of the scaled-indicator is fixed to the sample mean of the scaled-indicator at the first time point. If the standardization is based on the effect-coding method, the sum of loadings is constrained to the sum of loadings obtained in the first step, and the sum of intercepts is constrained to the sum of the sample mean of all indicators at the first time point. We also propose a first-order LGM standardization procedure based on the composite scores. First, we standardize the composite scores at the first time point, and make the same linear transformation of the composite scores at the other time points. Then we establish the first-order LGM, which is comparable with the second-order LGM scaled by the latent-standardization method.

The scaling methods of second-order LGMs and their comparable first-order LGMs are systematically summarized. The comparability is illustrated by modeling the empirical data of a Moral Evasion Questionnaire. For the scaled-indicator method, second-order LGMs and their comparable first-order LGMs are rather different in parameter estimates (especially when the reliability of the scale-indicator is low). For the effect-coding method, second-order LGMs and their comparable first-order LGMs are relatively close in parameter estimates. When the latent variable at the first time point is standardized, the mean of the intercept-factor of the first-order LGM is close to 0 and not statistically significant; so is the mean of the intercept-factor of the second-order LGM through the effect-coding method, but those through two scaled-indicator methods are statistically significant and different from each other.

According to our research results, the effect-coding method is recommended to scale and standardize the second-order LGMs, then comparable first-order LGMs are those based on the composite scores and their standardized models. For either the first-order or second-order LGM, the standardized results obtained by modeling composite total scores and composite mean scores are identical.

latent growth model, composite score, scaling method, scaled-indicator, effect-coding, latent-standardization

2023-02-06

* 国家自然科学基金项目(32171091)、教育部人文社会科学重点研究基地重大项目(22JJD190006)资助。

并列第一作者: 王一帆

温忠麟, E-mail: wenzl@scnu.edu.cn

B841