基于LQR算法的一阶倒立摆控制系统设计与仿真

刘昱鑫,沈 阳,曹玉波

(1.吉林化工学院 信息与控制工程学院,吉林 吉林 132022;2.涂易工业技术(上海)有限公司 电气部,上海 201821)

倒立摆具有快速、非线性、强耦合等特点,通过对倒立摆系统的研究,能够揭示机器人、宇宙飞船和水下舰艇等系统中存在的控制问题[1],因此对于倒立摆的研究具有重要现实意义。近年来,国内外许多学者利用最优控制方法对倒立摆系统进行了深入的研究。

将LQR控制器应用于一阶倒立摆系统[2],使用Simscape对一阶倒立摆进行建模与控制仿真,验证了系统具有良好的稳定性与鲁棒性[3]。

1 倒立摆的建模

1.1 倒立摆的数学建模

使用牛顿-欧拉法对一阶倒立摆系统进行动力学建模。在忽略空气阻力和摆杆转动阻力的情况下,滑块可以在导轨上水平移动,摆杆可以在XOZ平面一维转动。对一阶倒立摆受力分析如图1所示,规定X轴正方向为正。

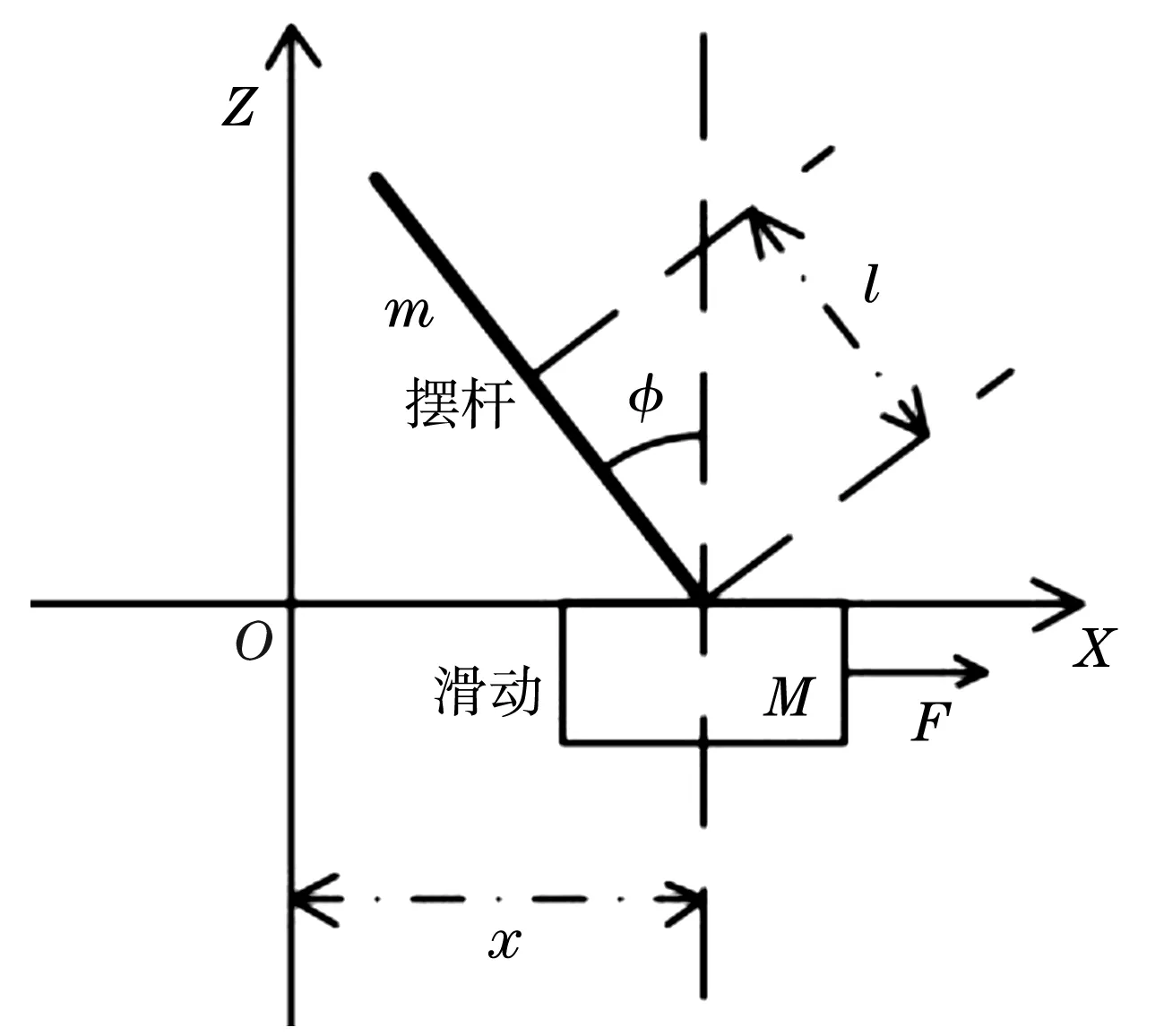
图1 倒立摆受力分析图

对一阶倒立摆水平方向进行受力分析,可得

(1)

对一阶倒立摆竖直方向进行受力分析,可得

(2)

其中F是加在滑块上的力;φ是摆杆与垂直方向的夹角;M是滑块质量;m是摆杆质量;μ是滑块水平移动的摩擦系数;l是摆杆重心到转动点的距离;J是摆杆的转动惯量。

对一阶倒立摆在平衡点附近进行线性化,得到线性系统的微分方程为[4]

(3)

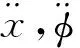
(4)

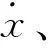
一阶倒立摆各参数具体数值如表1所示。

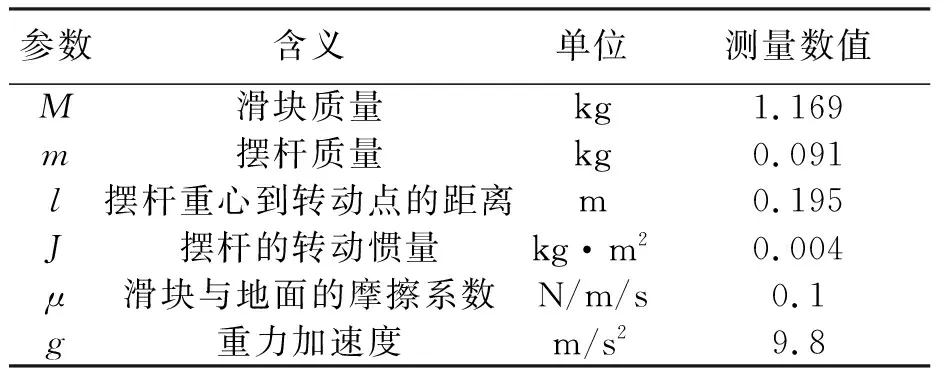
表1 实际参数表

将实际数据代入,得到系统状态空间表达式为

(5)

其中,

对一阶倒立摆系统稳定性进行分析。使用Matlab的eig函数可以求出一阶倒立摆的开环系统极点为(0 -0.08 -4.91 4.91)。系统有落在S平面右半轴的极点,因此一阶倒立摆系统属于不稳定系统。

对一阶倒立摆能控能观性进行证明,系统是四维的,n=4;其能控矩阵C0,能观矩阵O为

C0=[BABA2BA3B]Rank(C0)=4=n,

O=[CCACA2CA3]Rank(O)=4=n,

系统能控,说明滑块位移、滑块速度、摆杆角度、摆杆角速度四个状态变量都可被输入控制。系统能观,说明系统的四个状态变量都可由输出观测。

1.2 一阶倒立摆模型在Simscape环境中的实现

Simscape是基于Matlab/Simulink的可视化物理系统仿真环境[5]。采用物理拓补网络方式构建系统模型,每一个模块都对应一个实际物理元器件,模型构建完成后会自动计算出系统的动态特性数学方程,代替了利用复杂数学公式建模的方法,直观地显示出物理系统的结构关系,非常适合对复杂过程开展物理建模和计算求解。

基于Simscape建立的一阶倒立摆物理模型,如图2所示。

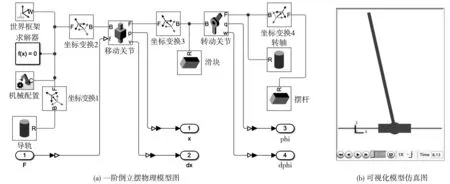
图2 基于Simscape的一阶倒立摆物理模型图

2 一阶倒立摆LQR控制器设计与仿真

由1.1节可知,系统不稳定但系统能控能观。使用线性状态反馈控制,能使系统处于稳定状态。令输入变量为状态变量的-K倍[6]：

u(t)=-Kx(t),其中,K=[k1k2k3k4] ,

(6)

(6)式便是状态反馈控制表达形式,难点在于求解状态反馈增益矩阵K。将(6)式代入系统的状态空间方程中：

(7)

控制系统结构图如图3所示。

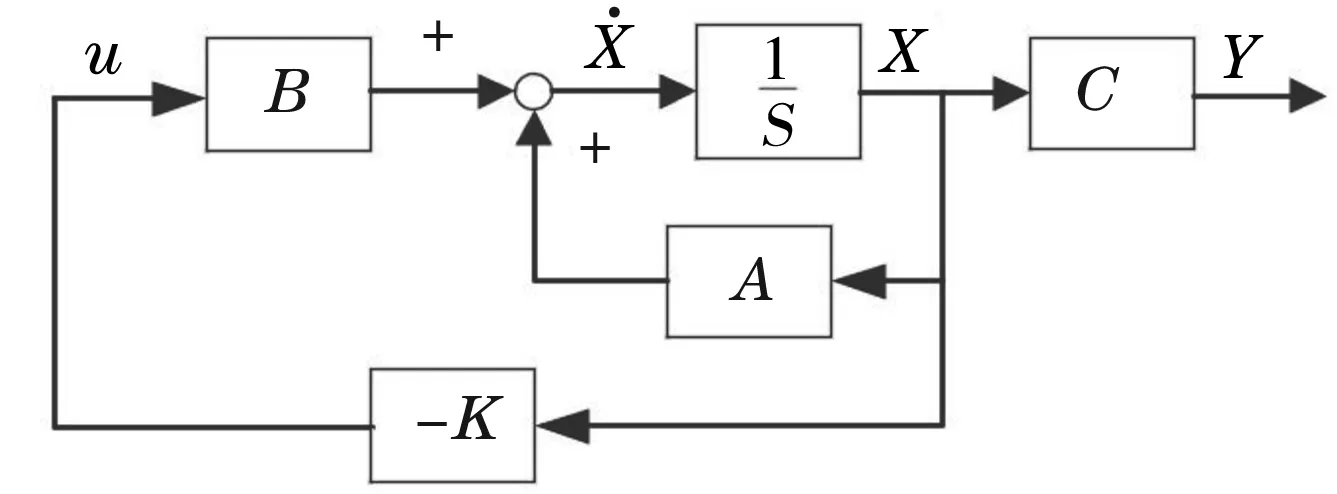
图3 控制系统结构框图

2.1 倒立摆系统LQR控制器的设计

LQR(Linear Quadratic Regulator)控制器又称线性二次型调节器。线性二次型最优控制设计是基于状态空间技术设计一个优化动态控制器。通过状态空间形式给出的线性系统,设计状态和控制输入的二次型目标函数,在线性系统约束条件下选择控制输入,使得二次型目标函数达到最小[7]。

为了求出最优反馈增益矩阵,引入代价函数(Cost Function)

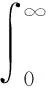
(8)

控制器设计的目标是选择合适的K,从而得到Jmin(代价函数的最小值)。矩阵Q和R分别是状态变量和控制量(输入量)的权重矩阵,都是正定的对称矩阵。一般情况下Q和R会选择为对角矩阵,且对角线上的元素都大于0,

代入式(8)可得

(9)

观察(9)式可以发现不同的权重系数对代价函数的影响。例如当q1远大于其他权重值时,在求Jmin的时候就会更关注x的变化,会让它在最短时间内稳于0。反之,如果r比较大,在求解的过程中就会更加关注u的值[8]。

将(6)式代入代价函数中,

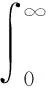
(10)

假设存在一个常量矩阵P,使得

(11)

将其代入代价函数可得

(12)

因为积分上限为正无穷,系统处于稳定,x→0。由莱布尼兹公式可知,将代价函数展开后前面的负号会被消去。x(0)代表初始条件。

将(7)式代入(10)式并展开得

xT[(A-BK)TP+P(A-BK)+Q+KTRK]x=0 ,

(13)

因为该二次型有解,所以：

ATP-KTBTP+PA-PBK+Q+KTRK=0 ,

(14)

令K=R-1BTP,得到黎卡提方程：

ATP+PA+Q-PBR-1BTP=0 ,

(15)

其中R,B已知,根据黎卡提方程可求出P,继而求出K。

2.2 倒立摆系统LQR控制器的仿真

将1.2节搭建的Simscape仿真模型封装成模块,并搭建出基于状态反馈的LQR控制器。由1.1节可知系统的状态矩阵A,输入矩阵B。代价函数的权重取值如表2所示。

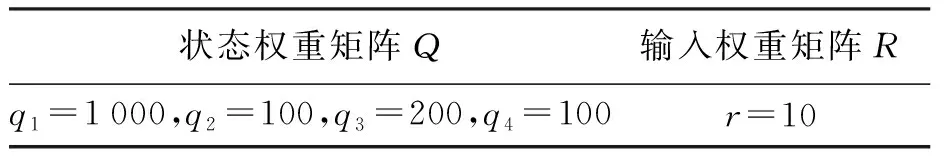
表2 权重取值

将上述条件带入2.1节求解过程,求出K=[-10,-10.4,59.47,12.6]

设摆杆与竖直方向初始夹角为5°,将求出的反馈增益代入系统,目标是将它控制到平衡位置。仿真结果如图4所示。

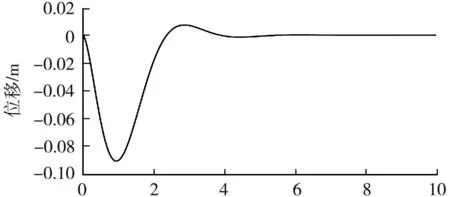
t/s(a) 滑块位移随时间的变化

通过仿真结果可以发现,LQR控制器成功地将一阶倒立摆系统稳定到了平衡点。控制效果良好,位移与摆杆角度调节时间均小于5 s;摆杆角度超调量足够小,稳态误差满足要求,上升时间不超过1 s。说明LQR控制器实现了一阶倒立摆系统的控制,且系统具有良好的稳定性与鲁棒性。

3 结 论

倒立摆是一个复杂不稳定的、带有非线性和强耦合性的系统,对倒立摆系统的研究是学习控制理论最合适的装置之一。本文对一阶倒立摆进行受力分析,得到状态空间方程,并基于Simscape建立了一阶倒立摆的模型。在此基础上设计了LQR控制器对一阶倒立摆进行控制,成功地将一阶倒立摆系统稳定在了平衡点。