基于机器学习的非定常流场网格自适应
2023-08-03李彩云刘学军吕宏强
李彩云,安 慰,刘学军,*,吕宏强
(1.南京航空航天大学 计算机科学与技术学院,模式分析与机器智能工业和信息化部重点实验室,南京 211106;2.南京航空航天大学 航空学院,南京 210016)
0 引言
计算流体力学(computational fluid dynamics,CFD)的任务是数值求解流体力学控制方程,其已被广泛应用于航空工程、生物科学工程、水利工程等所有涉及流场流动、热交换等现象的领域。计算网格的质量直接影响数值计算的收敛性和计算精度。对于简单流场,人工生成的网格通常可以满足需求。然而,复杂的非定常流场具有多尺度结构,大多数情况下在计算前无法给出合适的网格,仅凭人工经验调整网格,准确度低,因此有必要研究网格自适应技术以提高求解精度。
网格自适应技术主要有3 种:局部加密法(H 型)、局部升阶法(P 型)和移动网格法(R 型)。H 型方法是根据某些误差指标局部细化和粗化网格,较常见的方法有基于误差估算的方法[1]、伴随方程法[2]等,通常需要增加大量网格节点且改变网格拓扑结构。P 型方法是在数值解剧烈变化的区域使用更高阶的数值格式,以提高计算精度;通常和H 型方法结合使用,如求解具有传热效应的不可压缩流的HP 型自适应算法[3]。这两类自适应方法分别在增加网格节点和高阶计算方面增大了计算复杂度。R 型方法通过某种策略移动网格节点,使网格节点在流场解变化强烈的区域更密集,同时不改变网格量和网格拓扑结构,因此R 型方法在提高计算精度的同时,不会造成计算量的增加。
Cao 和Huang[4]总结和比较了各种R 型自适应方法,将其分为两类:基于速度的方法和基于位置的方法。前者建立关于网格速度的网格方程,通过对速度场积分得到网格节点的位置。如Miller 等[5]提出的移动有限元法(moving finite element,MFE),通过最小化网格速度xt和网格函数的L2 范数生成移动网格;Thomas 和Lombard[6]提出集合守恒定律(gather conservation law,GCL)方法,根据网格速度xt的雅可比矩阵Jt所满足的恒等式得到移动网格。虽然这类网格自适应方法的网格密度和控制函数之间的关系更直接,但因为自适应网格是网格速度场时间集成的结果,后续时间步的网格移动受前期网格移动结果的影响,最终可能产生倾斜网格[4]。基于位置的方法直接控制网格节点的坐标,一个典型方法是变分法,通过求解泛函的极小值得到网格计算域到物理域的映射,从而得到移动后网格节点的位置。这类方法中,Winslow[7]提出了一种基于变量扩散的等势方法求解泛函的极小值;在此基础上,Thompson 等[8]使用泊松方程控制网格密度与方向改进泛函;Brackbill 和Saltzman[9]提出了一种结合了网格密度、平滑度和正交性的网格泛函方法;Dvinsky[10]使用谐波映射量作为网格函数;Brackbill[11]将Winslow 的方法与调和映射法结合,提出了一个同时考虑网格密度和对齐条件的泛函。Huang[12]使用各向同性和等分布条件构建网格泛函[13],用于研究一种新的离散化和求解策略[14],保留了连续函数的基本几何结构并取得了较好结果。针对CFD 流场网格没有准确的函数拟合流场值的问题,Wu 等[15]对Huang[14]的方法进行改进,用反向传播神经网络(backpropagation neural network,BPNN)回归模型替代拟合函数法,在二维定常流场自适应网格上取得较好结果。
现有针对非定常流场数值模拟的网格自适应方法通常每隔一段时间步就进行一次网格调整,网格函数利用每个周期初始时间步的流场解进行拟合。因此所得网格会滞后于流场解,需要不断地自适应处理以减少时间差。Tang[16]在每段时间步上进行多次自适应处理,使用插值方法获得网格解,从而减小时间差,但是存在数值解插值导致误差增大的问题。韩志熔等[17]用流场速度的紊乱度作为指示变量来构造网格自适应指示函数,采用H 型网格自适应方法提高局部网格密度;这种方法提高了计算精度,但同时也存在H 型方法增大计算量的问题。Jacobson 等[18]提出了跨声速颤振的网格自适应方法,基于表示标量场插值误差的多尺度度量进行网格调整。
本文提出采用间断伽辽金(discontinuity Galerkin,DG)有限元法[19]对可压缩Navier-Stokes(N-S)方程进行数值离散,实现高阶精度;将变分法和机器学习相结合,实现非定常流场网格的一次性网格自适应,以满足所有时间步的CFD 计算;同时避免在非定常计算过程中因调整网格而涉及的几何守恒律问题。具体而言,在初始网格上使用DG 方法试算一段时间,直至出现周期性非定常现象,然后统计非定常流场中局部数值解精度的间断量;由网格信息和间断量训练BPNN 回归模型;使用MMPDE(moving mesh partial differential equation)变分法进行网格自适应,并优化网格质量,得到最终的自适应网格。该方法有望缓解传统网格自适应存在的计算量巨大的问题,在不改变CFD 计算复杂度的情况下提升计算精度。
1 方法介绍
图1 给出了基于机器学习的非定常流场网格自适应框架(具体细节在2.2 节介绍)。首先在初始网格T0上使用DG 有限元方法统计得到间断量Re0;根据初始网格和间断量训练BPNN 回归模型,得到任意节点位置和间断量的映射关系;然后使用MMPDE 变分法移动网格,每次移动后的网格Ti通过回归模型预测得到对应网格节点间断量Re,i,重复n次后得到网格Tn0;最后通过Laplacian 平滑法对Tn0进行质量优化,得到新的网格Tn,并返回至CFD 计算模块中求解N-S 方程。本节对所用到的方法进行分别介绍。

图1 基于机器学习的非定常流场网格自适应的框架Fig.1 The framework for grid adaptation of unsteady flow fields based on machine learning
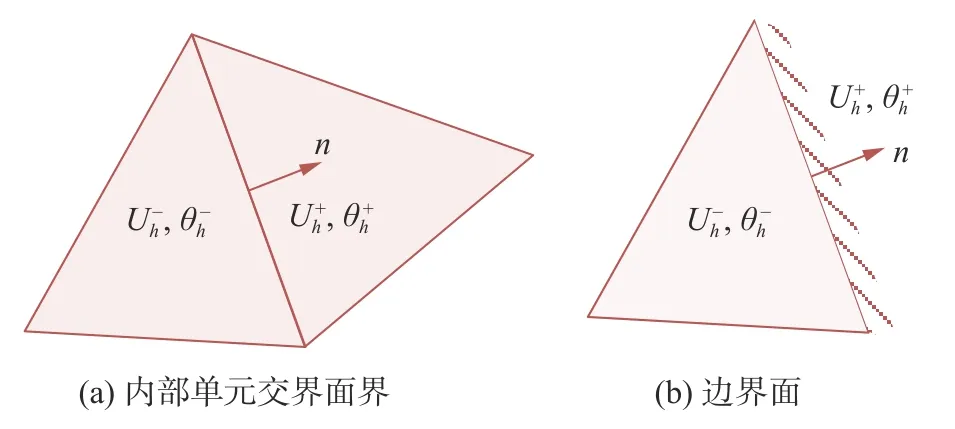
图2 交界面的左右单元变量Fig.2 Left and right cell variables of the interface
1.1 DG 有限元方法
DG 方法是典型的高阶数值方法,通过提高单元上数值解多项式的阶数,增加相应单元上解函数的自由度来提高空间精度。该方法易于处理任意网格和复杂几何区域,适用于网格自适应[20]。
可压缩黏性流动的N-S 方程可以表示为:
为了使上述方程组封闭,补充理想气体状态方程p=(γ −1)ρ[E−(u2+v2)/2],常态下空气的比热为γ=cp/cv=1.4。本论文采用Bassi 和Rebay 提出的 BR2 格式,引入辅助变量 Θ=∇U。对式(1)采用DG 有限元方法进行空间离散,得到守恒变量的高阶格式:
式中,uj(t)代表方程变量,表示每个单元内数值解的自由度,ϕj(x)是对应的基函数,N表示p阶时基函数的个数。控制方程的解U在空间和时间上分别进行离散,其中uj(t)是关于时间的函数,而 ϕj(x)为空间离散的函数。
对式(1)分部积分得到:
式中,∂K为单元K的边界集合,e为单元K的任意一条边界,为单元K上的基函数,k为该基函数的最高阶数。
本文采用总体提升因子Rh表征单元的间断量。由于Rh在单元内是多项式分布,这里取Rh对应ρ的量在单元内积分得到Re,即网格间断量。记Rh对应 ρ的量为Rh,1,则有:
其中,Se为单元面积,||·||2为L2 范数。
为了说明间断量与流场数值之间的关系,图3 给出了二维圆柱绕流结构网格在Ma∞=0.2、Re=200 下的计算结果。可见高间断量区域与马赫云图中的数值变化剧烈区域相对应,表明尾流区间断量大的网格单元局部数值解精度不足,需要移动网格节点实现局部加密。
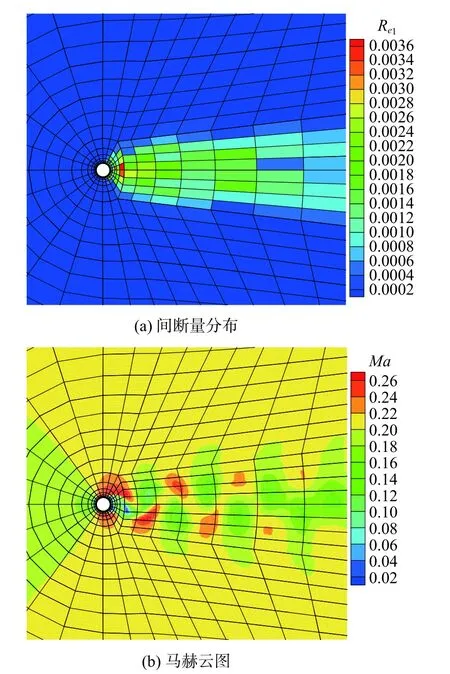
图3 圆柱绕流间断量分布及马赫云图(Ma∞=0.2,Re=200)Fig.3 Discontinuity distribution and Mach cloud diagram of flow around the cylinder (Ma∞=0.2,Re=200)
1.2 基于MMPDE 的变分法移动网格
1.2.1 模型介绍
物理域Ω的网格Th有N个单元,每个单元记为K,节点记为X,节点X上的值由网格函数u=u(x,t)得到。固定边界节点、移动内部网格节点,使其符合函数值分布规律。对应计算域 Ωc中的网格Tc,h有相同单元数,每个单元Kc的节点记为 ξ,Th网格节点和Tc,h网格节点的对应转换关系为x=x(ξ)、ξ=ξ(x)。为防止出现网格交叉或折叠,后面讨论使用转换 ξ=ξ(x),计算网格节点上的值为=u(x(ξ))。从计算网格单元Kc到物理网格单元K有可逆仿射映射FK:Kc→K,使得K=FK(Kc)。
1.2.2 度量张量及MMPDE 变分法
利用插值误差估计可以获得最佳度量张量M[12]。首先考虑在简单情况下,对于函数u=u(x),任意单元K的顶点ai,i=1,···,n的线性拉格朗日插值为:
式中基函数 ϕi为线性拉格朗日多项式,满足:
记单元K的中点为XK,根据泰勒定理,将u(x)展开并根据特征分解性质和范数性质,对任意q∈[1,∞],插值误差可最终表示为:
式中,H(u,xK)为xK处的海森值,为FK的雅可比矩阵,h.o.t.表示高阶项,常数C=O(1)。
由于各向异性方法可以比各向同性方法提供更清晰的误差界限,特别是当物理解显示各向异性特征时,例如在一个方向上变化比其他方向更快,所以各向异性误差界限提供了许多自适应算法分析设计所需的信息。采用索伯列夫空间中的插值理论,结合各向异性方法,将式(6)插值误差范围改为:
根据等分布和对齐条件[14],满足M均匀网格需要符合下列条件:
结合式(4)得到度量张量为:
要注意的是,这里的项HK,α是单元K处的海森矩阵。即,首先计算网格节点处函数解的梯度,由此得到的MK控制网格节点向梯度值大的位置移动。根据均匀分布原理,本文目标是得到M度量下的均匀网格。变分法移动网格即利用求解泛函的极值来确定生成网格所需的坐标变换。为避免其离散化过程丢失泛函的几何结构,用物理域和计算域对应的网格单元映射替代传统的节点坐标变换,并使用MMPDE求解泛函极值,即基于MMPDE 的变分移动网格方法[14]。
带有M的网格泛函的通用形式为:
式中,J=∂ξ/∂x是 ξ=ξ(x)的雅可比矩阵,G是给定的光滑函数(对每一个参数)。由计算网格单元Kc到物理网格单元K的映射关系,式(11)可以直接近似为:
式中,Tc0,h为 Ωc上的参考网格,Φh为当前计算网格到物理网格的变换函数。
1.3 BPNN 回归模型
由于前文介绍的MMPDE 变分法需使用网格函数计算每次移动后网格节点上的函数值,无法直接应用于CFD 中,因此大部分自适应网格方法采用特定函数拟合流场,如Cao 等[22]用函数u(x,t)=tanh[50(3x−|y|−t)]表示翼型激波位置。而在CFD 数值仿真中,非定常流场数值变化剧烈、区域复杂,难以用某种特定形式的函数进行拟合,因而MMPDE 变分法无法直接用于CFD 流场网格自适应。结合1.1 节介绍的DG有限元法,本文提出采用衡量网格单元计算精度的间断量数值作为网格自适应的依据;考虑到神经网络具有较强的逼近非线性函数的能力,并具有自适应学习、较强的鲁棒性和容错性的特点,本文使用神经网络拟合非线性的间断量,为CFD 流场网格自适应提供了一种新的有效途径。tanh(x)=(ex−e−x)/(ex+e−x),Sigmoid 函数:f(x)=1/(1+e−x),Relu函数:R elu=max(0,x)等。
神经网络的输入层和输出层神经元个数分别由输入和输出数据维数确定,这里输入数据为网格节点坐标,输出数据为网格节点对应的间断量;隐含层层数和每层神经元个数根据经验和实验测试确定。为保证神经网络实现非线性拟合,每个神经元需选用一个非线性函数作为激活函数。关于不同激活函数的研究,详见文献[23]。常用的激活函数有Tanh 函数:
反向传播(backpropagation,BP)神经网络是一种建立在梯度下降算法基础上的多层前馈神经网络,用输出层神经元的预测误差反向估计上一层隐含层神经元的预测误差,继而逐层将误差从输出层反向传播到隐含层,最后到输入层,从而实现对连接权重的调整。权值调整差值为:
式中,负号表示梯度下降,η为学习率,∂E/∂wi为误差关于当前权值的偏导数。使用链式法则可以求出误差对每个神经元权值的偏导,由式(14)得到新的权值,继续正向传播,进行下一次权值调整,直到网络的输出误差小于既定值,或者训练次数达到预设的学习次数为止。更多关于BPNN 的细节,如初始化权值、网络结构等,见文献[24-25]。
2 基于BPNN 的非定常流场网格自适应方法
网格划分是数值模拟至关重要的一步,它直接影响着后续数值计算结果的精确性。一方面由于流动的连续性被离散化,数值模拟的精度取决于网格的节点密度和分布;另一方面,网格单元的形状(包括偏斜率、长宽比等)对数值模拟精度也有重要影响,如偏斜率(skewness)为实际节点形状与同等体积等边形节点的差别,高的偏斜率会降低解的精确性,并降低收敛性。本节基于边界网格正交性原则和Laplacian网格光滑方法提高网格质量,提出基于BPNN 的非定常流场网格自适应方法。
2.1 Laplacian 网格平滑
在黏性流场中,边界附近流动参数变化剧烈,且通过数值求解椭圆型方程生成的曲线坐标系的坐标线与边界耦合,所以边界网格要求满足正交性条件,使用细密的贴体网格划分。考虑到初始网格的附面层网格有相对成熟的网格生成规范,在自适应调整过程中需固定附面层网格节点Xfix,否则可能出现附面层网格偏斜率过大导致离散误差增大的情况(如图4)。此外,畸形网格不仅影响精度,而且可能导致计算不收敛,所以在移动过程中应尽量提高网格质量。本文采用Laplacian 光滑法优化网格形状。
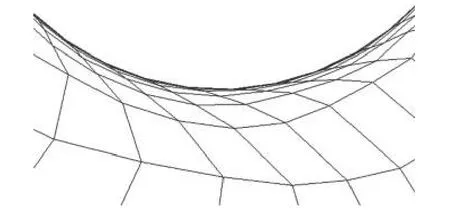
图4 附面层网格偏移Fig.4 Boundary layer grid offset
Laplacian 光滑将节点移动到其邻接单元中心,如图5 所示,节点I的坐标xi变换公式为:
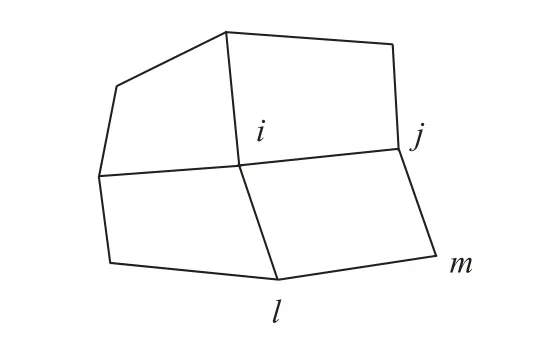
图5 Laplacian 光滑邻接单元示意图Fig.5 Schematic of Laplacian smooth adjacency unit
式中,∂K为xi邻接单元集合,|∂K|为邻接单元个数。式(15)控制节点向密度大的方向光滑,因此可以避免光滑导致网格密度特征损失,且附面层网格基本维持单元特征。
对于狭长形状的网格,上述方法可能出现无效的移动结果,这里引入单元质量概念[9]度量网格质量好坏。网格质量通常选取为网格单元的最大角度差,复杂方法如网格外接圆半径、变形矩阵等应用也较为广泛[11]。这里网格质量根据单元角度定义,如四边形平面角度αi(i=1,2,3,4),定义 ηi=sinαi,则单元质量取:
式(16)可有效识别单元中是否出现负角。若单元质量提高则移动网格节点,否则移回距离原节点的1/2 位置;移动次数达到预设上限或者单元质量差值达到阈值,则光滑停止。
2.2 基于BPNN 的非定常流场网格自适应方法
为了使移动网格方法独立于网格函数,本文采用回归模型代替误差估计方法[13],其训练过程如图6所示(具体网络参数见3.3 节)。T0为初始网格,Re0为DG 有限元方法在初始网格T0上离散N-S 方程求解一段时间所得的网格间断量。由T0和Re0训练BPNN 回归模型,网格节点坐标为模型输入数据,节点对应统计间断量为模型输出数据。
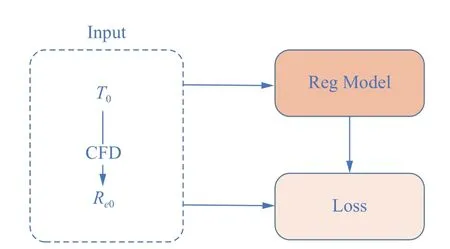
图6 回归模型的训练过程Fig.6 The training process of the regression model
根据间断量进行网格自适应,需对变分法中的度量张量(式(10))进行修改:
将上述训练所得回归模型与变分法移动网格相结合,每次网格移动的节点坐标通过回归模型预测当前位置的函数值。图7 给出第n+1 次迭代过程,为当前物理网格,为回归模型对预测出的网格间断量,为给定的参考网格。算法迭代过程如下:
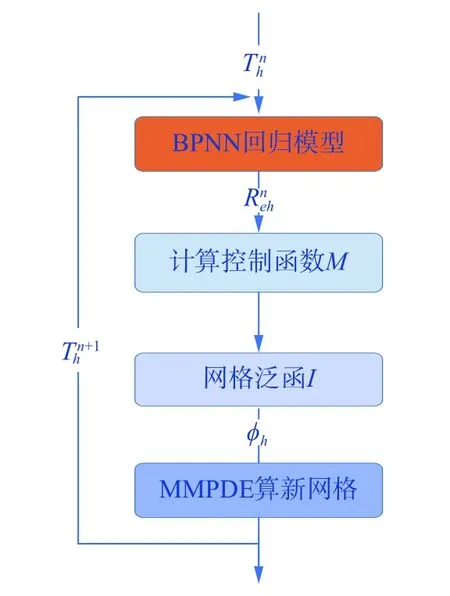
图7 基于BPNN 回归的变分法移动网格Fig.7 Variational Moving Grid Based on BPNN Regression
5)经过N次迭代后,得到最终自适应物理网格。
在迭代过程中,网格节点数和单元数保持不变。网格自适应后,使用Laplacian 平滑方法提高网格质量,整体流程如图8 所示。由图8 可见,本文提出的基于机器学习的非定常流场自适应方法完全独立于CFD 计算。在初始网格上采用DG 有限元法离散N-S 方程,统计得到网格间断量,输入到基于机器学习的网格自适应模块中;自适应过程中,采用回归模型代替CFD 计算获得每次移动后的网格节点值;自适应模块所得网格节点位置信息返回到CFD 计算中,重新进行非定常流场计算,完成一次性网格调整。
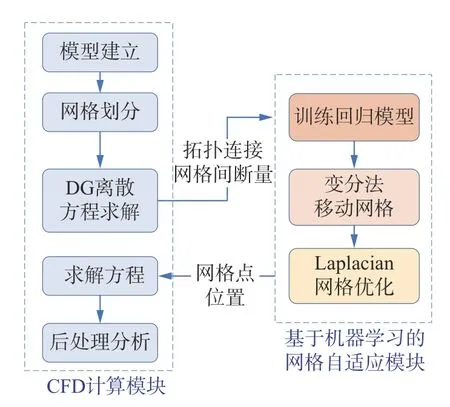
图8 算法迭代的整体流程图Fig.8 Overall flow chart of algorithm iteration
3 实验和分析
3.1 实验数据
本节基于DG 有限元法对二维圆柱绕流进行数值模拟,采用2.2 节提到的基于BPNN 的非定常流场网格自适应方法测试。来流条件为Ma∞=0.2、Re=200。壁面采用无滑移绝热边界条件,远场采用特征边界条件,本算例采用结构网格进行计算,单元总数为868,节点数为917,第一层网格节点的物面距为圆柱直径的0.01。采用四核并行计算,如图9 所示,分区网格单元数分别为213、211、211 和223,负载较为均衡。时间步长取 Δt=0.01,时间离散采用一阶隐式向后差分格式(BDF),空间离散选取三阶DG 方法。试算一段时间直到出现如图10 所示的1 个周期的非定常流场,统计所得网格间断量如图11(a)所示。
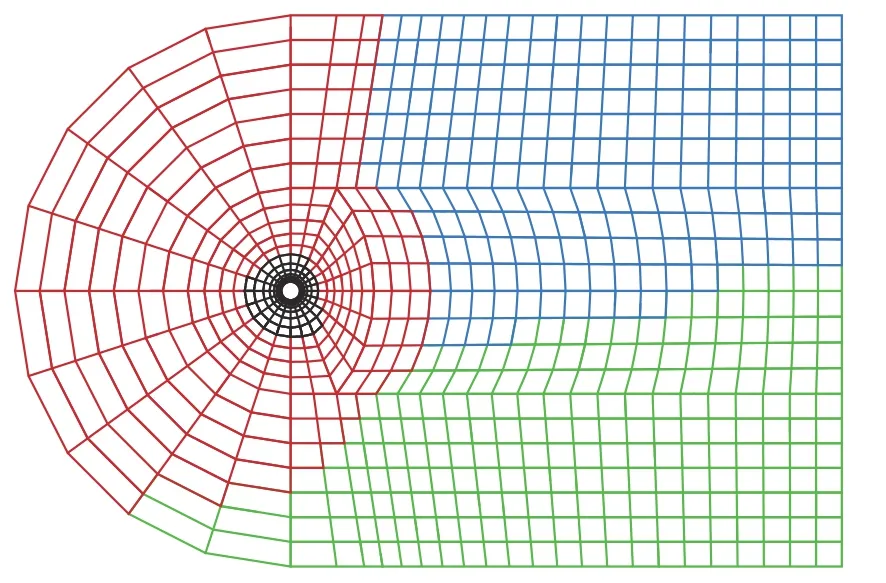
图9 二维圆柱绕流初始网格Fig.9 Two-dimension initial grid of flow around the cylinder
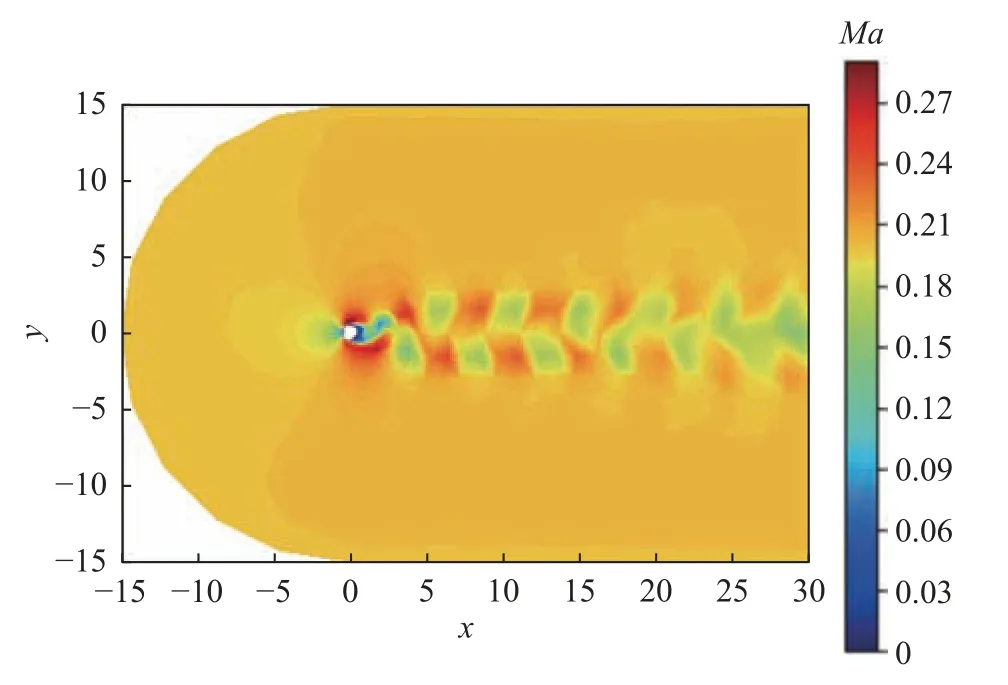
图10 采用结构初始网格计算得到的非定常马赫云图Fig.10 Unsteady Mach cloud obtained by using structure initial grid computation
3.2 数据预处理
由于初始值的影响,图11(a)中远场间断量增大,需要对数据进行处理并做平滑,结果如图11(b)所示。由于远场附近间断量均接近0,所以对应远场附近度量张量M大小相近(如图12(a)度量张量二维矢量图),根据均匀分布准则,对间断量进行变换。由图11(b)可知,圆柱尾部的间断量数值在y轴方向符合高斯概率密度函数(PDF)曲线,整体在x方向符合高斯累积分布函数(CDF)曲线,因此对间断量Re进行预处理,对应的控制度量张量M大小为:
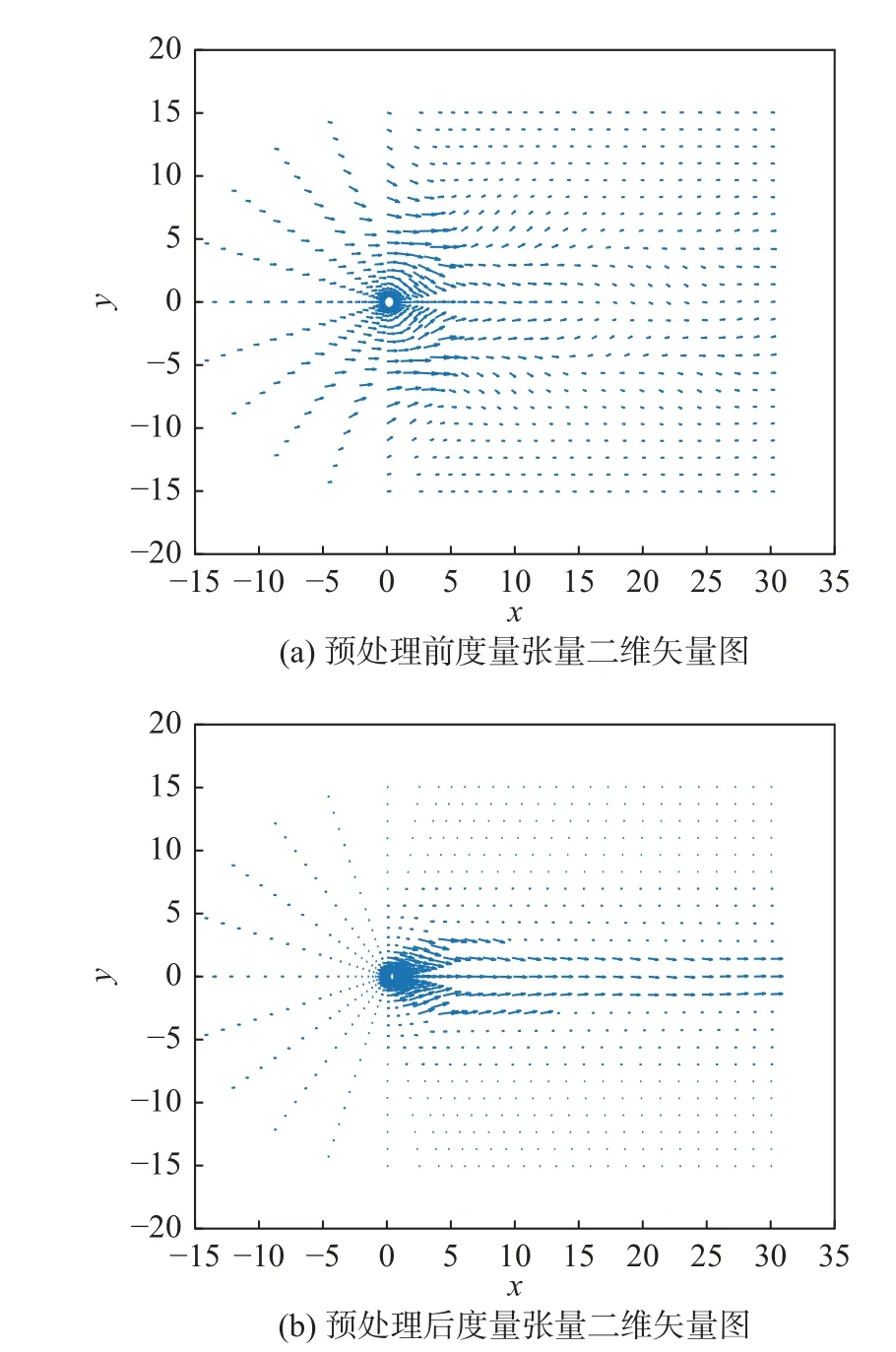
图12 预处理前后度量张量示例Fig.12 Example of metric tensors before and after preprocessing
式(18)中,用权重系数λ1、λ2保持间断量Re特征,取期望 µPDF1、µCDF1为 0,标准差 σPDF1、σCDF1分别为5 和1;预处理后的间断量如图11(c)所示,其空间分布更能合理反映流场的高梯度变化特性,且适用于MMPDE 网格自适应方法。式(19)中,用权重系数λM控制放缩M的幅度,取期望 µPDF2、µCDF2为0,标准差 σPDF2、σCDF2分别为8 和1,对应度量张量二维矢量如图12(b)所示。另外,由于物面附近度量张量较大,且呈线性变化,所以固定附面层网格节点时,外层单元在网格自适应过程中不会产生畸变。
3.3 神经网络设置
BPNN 训练数据为初始网格上917 个节点坐标及对应统计间断量,隐含层和输出层的激活函数隐含层分别为Tanh 函数和Sigmoid 函数,训练误差目标值为Pgoal=0.000 01,学习率为lr=0.01,最大训练次数为Pepoch=1 000,验证次数为Pmaxfail=100。
一般情况下,BPNN 网络层数加深容易导致梯度爆炸和梯度消失的问题,因此隐含层的数量通常设置为小于4。本文首先探究了适用于预测网格节点间断量的网络结构,选择预测结果的均方根误差(RMSE)作为网络结构的评价指标,其隐含层计算方式为:
式中,yi和分别为真实值和回归模型的预测值,m为样本个数。图13 显示了在相同数据集上对不同隐含层设置的神经网络进行十折交叉验证的RMSE 箱线图。由图13 可知,具有一个隐含层的神经网络预测误差较大,这表明出现了欠拟合现象。随着该隐含层神经元数量的增加,预测误差逐渐降低;而增加隐含层也能够显著减小预测误差,并保持稳定隐含层;但当隐含层过多或每个隐含层的神经元过多时,会出现过拟合,从而导致预测精度降低。因此,本文选择三个隐含层[10,10,10]预测任意位置的网格节点间断量。
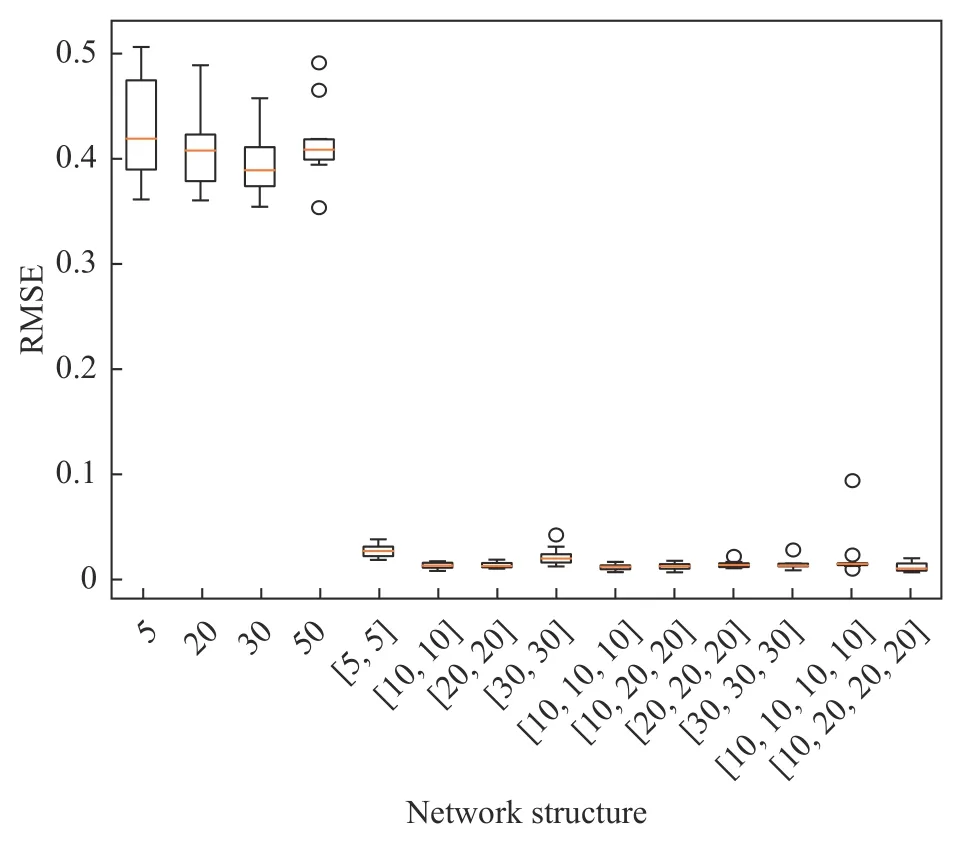
图13 神经网络结构选择箱线图Fig.13 Neural network structure selection boxplot
3.4 自适应结果分析
传统有限元网格的质量通常以翘曲度、扭曲角以及雅可比比率等参数指标来度量,而对于CFD 高精度方法的计算网格而言,网格质量由计算收敛所得数值解的精度来评价,网格质量过低会导致计算无法收敛。因此,本节以计算精度来分析评估网格质量。
为了探究间断量的数据预处理对网格移动结果的影响,本文应用基于BPNN 的非定常流场网格自适应方法,分别对有、无数据预处理的间断量进行网格移动。图14(a、b)分别标记了初始网格有、无预处理的不动节点和高间断量节点,图14(c、d)分别为调整后的对应网格,网格节点加密位置与高间断量区域相对应。
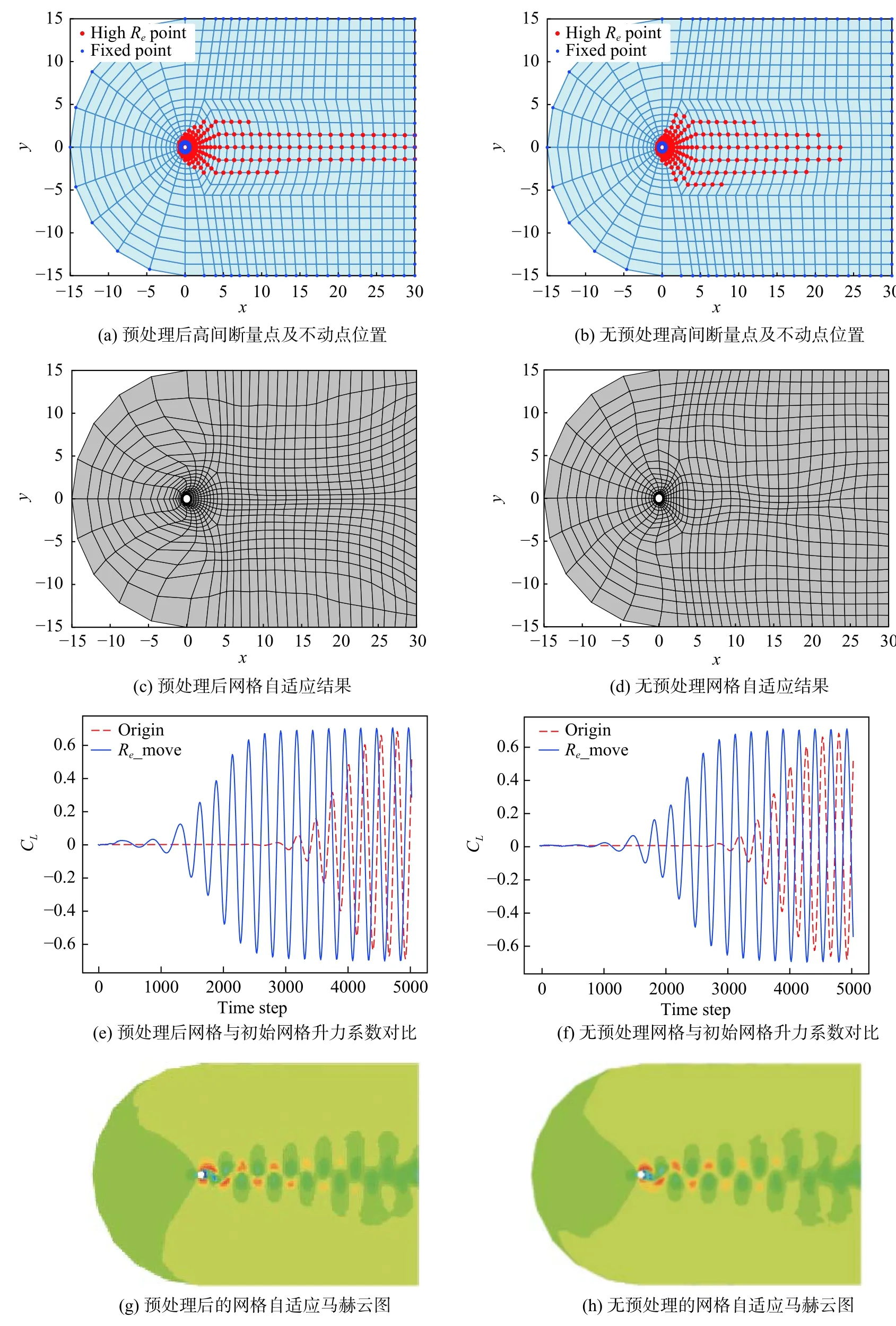
图14 有无预处理自适应网格结果对比Fig.14 Comparison of adaptive meshgrid results with and without preprocessing
将图14(c、d)中的网格节点位置信息返回至CFD 计算模块进行N-S 方程求解,计算条件与实验数据的相同,升力系数、表面压力系数等计算结果的输出周期为10 个时间步长。图14(e~h)显示了计算迭代5 000 步的对比结果。
图14(e、f)分别显示了有、无数据预处理的自适应网格升力系数曲线,相较于初始网格升力系数曲线(红色虚线),经两种方法调整后的网格升力系数曲线均提前出现非定常振荡。从统计意义上讲,圆柱绕流的合理网格分布应为上下对称,带有预处理流程的网格优化结果生成的最终网格基本符合上下对称特征。另外对于高阶DG 方法而言,高阶基函数在不同网格内的分布跟单个网格单元的节点编号相关,即对称网格单元中基函数的分布往往并不对称,导致上下两部分区域的数值解存在理论上的差别。因此,不同于有限体积法,采用高阶DG 方法进行非定常流场计算不会因网格对称而延迟或减弱非定常现象。从该圆柱算例的结果可见,经预处理的网格计算结果在1 000 步左右已经出现非定常效应,而未经预处理的网格计算结果在1 500 步左右才出现,说明数据预处理后的网格分布更合理,因此提高了计算精度。
图14(g、h)显示了分别采用两种网格计算5 000步得到的马赫云图,可见图14(g)尾流区清晰度高于图14(h)。根据间断量化指标,间断量较大的区域需要较密的网格分布;间断量较小的区域数值解相对光滑,网格可以稀疏分布。在圆柱绕流中,涡街区域需要更密的网格。对比结果显示,数据预处理后的自适应网格获得了更为精确的卡门涡街,可见预处理后的间断量可以更合理地反映流场结构的物理规律。
表1 给出了相同条件下,初始网格和有无数据预处理的自适应网格进行5 000 步计算的耗时情况。其中,用于CFD 计算的硬件设备为Intel Core i7-9700 CPU 3.00 GHz,采用 8 核并行计算;用于神经网络预测及网格自适应的硬件设备为Intel Core i9-10900K CPU 3.70 GHz,采用串行计算。从表1 可以看出,3 种网格的非定常流场计算耗时接近,自适应后的网格在提高计算精度的同时,没有明显降低计算效率,且数据预处理后的网格比未经预处理的网格计算耗时更少。

表1 初始网格和有无数据预处理的自适应网格计算耗时Table 1 CPU time of initial mesh and adaptive mesh with or without data preprocessing
综上分析,本文所提基于BPNN 的网格自适应方法适用于非定常流场网格调整。另外,基于DG 有限元方法统计获得的间断量指标需经过一定时间的非定常计算,该统计时长难以严格控制为整数周期或准周期,这一定程度上影响了网格优化质量。因此,本文提出的预处理过程旨在消除不同非定常计算时长对网格优化效果的影响,通过对数据进行预处理并控制度量张量M,使得网格自适应结果符合流场特征,从而提高计算精度。0
3.5 模型泛化性分析
本节采用更复杂的非定常流场算例进一步验证本文所提模型的泛化能力。该算例为相同来流条件(Ma∞=0.2、Re=200)下的圆柱绕流,采用四边形/三角形混合网格,由贴体的四边形结构网格和外场的三角形非结构网格构成,节点数为4 053,网格单元数为7 496,如图15 所示。采用一阶DG 方法,统计所得网格间断量如图16 所示。

图15 非定常圆柱绕流混合初始网格Fig.15 Hybrid initial grid of unsteady flow around the cylinder

图16 混合网格在Ma=0.2、Re=200 来流条件下的网格间断量Fig.16 Mesh discontinuity of hybrid grid at Ma=0.2,Re=200
BPNN 训练数据为初始网格节点及对应间断量,由于数据分布与前一算例相似,采用相同的网络参数即可得到较好的训练结果(见图17)。考虑到附面层网格有相对成熟的网格生成规范,因此在该算例中,附面层的四边形结构网格节点保持固定(见图15),自适应后的网格如图18 所示。初始网格和自适应网格分别在相同初始条件下进行30 000 步非定常计算,结果如图19~图21 所示。
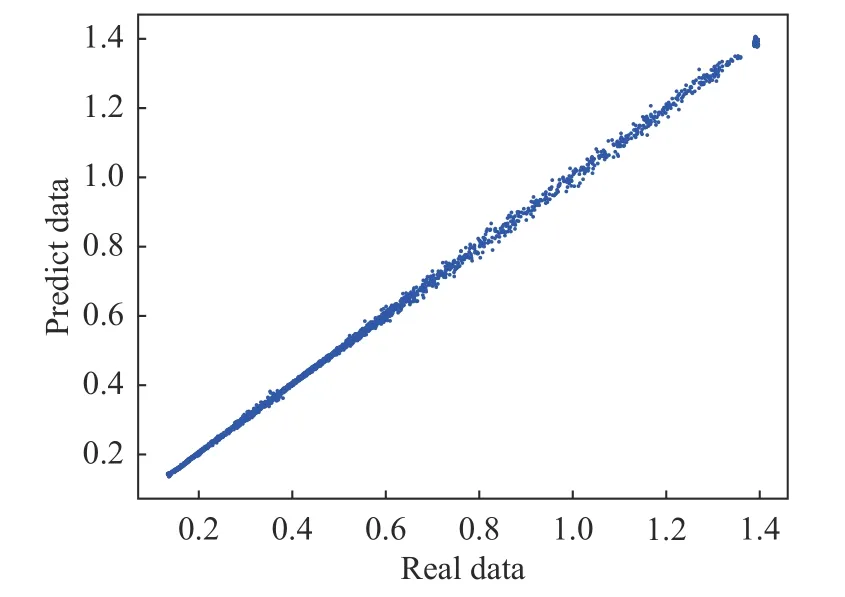
图17 BPNN 训练结果Fig.17 BPNN training results

图18 混合网格圆柱绕流自适应网格Fig.18 Adaptive hybrid grid of flow around the cylinder
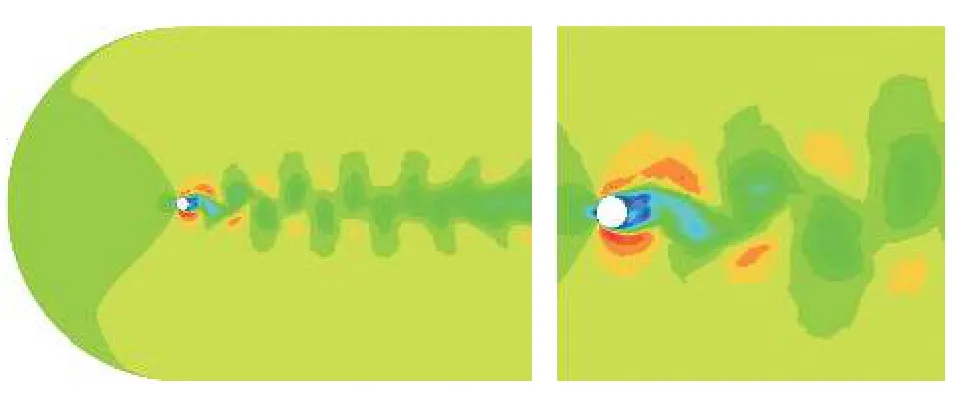
图19 采用初始网格计算得到的马赫云图Fig.19 Mach cloud obtained by initial grid computation
图19 和图20 分别为初始网格和自适应网格计算30 000 步后的马赫云图,可以看到,网格自适应方法在流场结构更复杂的涡街区域实现了网格的相对加密,计算所得的流场结构更清晰。图21 为升力系数曲线对比,可以发现,自适应网格升力系数曲线(蓝色实线)较初始网格升力系数曲线(红色虚线),提前出现了显著的非定常振荡。
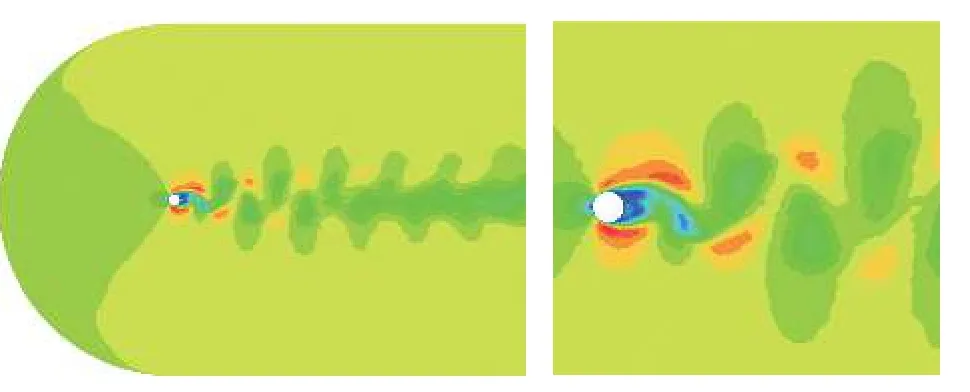
图20 采用自适应网格计算得到的马赫云图Fig.20 Mach cloud obtained by adaptive grid computation
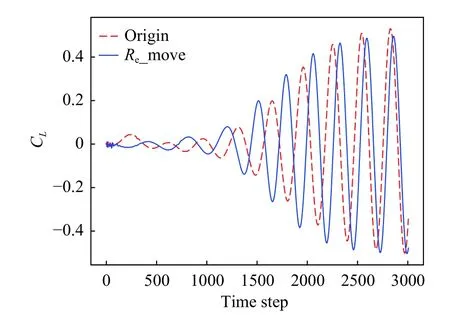
图21 初始网格和自适应网格下的升力系数对比Fig.21 Comparison of CL between the initial grid and the adaptive grid
表2 给出了自适应前后网格的非定常计算、BPNN训练与网格自适应步骤的耗时对比。相比表1,神经网络训练平均耗时随数据量增加呈线性增长。在处理更大规模的网格时,网格自适应所需的计算时间远小于非定常计算时间,因此本文所提网格自适应方法在提高计算精度的同时,能够保证计算效率。

表2 网格自适应前后的各种计算耗时Table 2 Different CPU time before and after grid adaptive
4 结论
CFD 高精度数值模拟结果依赖流场方程求解时的数值格式和计算网格质量。针对非定常流场计算网格调整困难的问题,本文研究了结合机器学习和变分法的移动网格方法,在不增加网格节点数且不改变拓扑结构的前提下,移动网格节点,具体方法为:基于DG 有限元方法,在原始网格上获得间断量指标统计值,采用机器学习方法进行一次性的R 型网格自适应,同时采用Laplacian 平滑法保证网格质量,并在调整后的网格上进行最终的非定常计算。整个过程不涉及几何守恒律问题,使得该网格自适应方法独立于CFD 计算,同时减少了非定常网格自适应的时间耗费。
本文通过圆柱绕流算例比较了调整前后二维圆柱绕流网格的非定常计算结果,涡街区域相对加密的自适应网格更早出现非定常现象,且流场结构更为清晰。该实验结果表明,间断量指标统计值可作为非定常流场网格自适应的参考依据,通过结合机器学习使得网格调整自动化、智能化,调整后的网格在保证计算效率的同时,提高了CFD 计算精度。
本文网格自适应方法以三角形(二维)为基础单元,任意网格单元可以剖分成三角形单元进行网格自适应,且移动过程中不产生负体积问题,能够保持原始网格的拓扑结构。因此,所提方法对网格单元没有限制,适用于结构网格、非结构网格以及混合网格。后续可以将本文方法拓展至三维,以四面体为基本单元进行网格自适应。
