车载机枪托架行进间发射动力学分析与优化

郁卫星,杨 臻,刘万川,张梦飞,景春温

(1.中北大学 机电工程学院,太原 030051;2.重庆建设工业(集团)有限责任公司,重庆 400054)

0 引言

托架是枪座上的主要承力构件,连接车辆和机枪。机枪行进间射击时,托架既要承受路面不平经车体传递的随机振动,也要承受机枪由于连续发射带来的后坐冲击力,导致它的受力情况非常复杂。其结构刚强度对武器系统射击精度等动态特性影响较大[1]。车载机枪在一些遭遇战中对中小目标有很好的火力压制作用,所以对其射击精度有较高的要求。为改善车载机枪在行进间射击的稳定性和可靠性,研究托架在随机路面振动和持续冲击作用下的力学性能并加以改善至关重要。

战车行进过程中路面状况和车速是影响车体振动的主要因素[2-3],车体振动冲击会经过托架传递到车载机枪上,通过改进托架摇架结构布局或增加支撑系统可以有效减小振动冲击对射击精度的影响[4-6],同时机枪发射时,后坐冲击也会对托架的刚度及疲劳寿命产生较大影响[7],所以本文对行进间射击时的托架进行力学仿真,能有效进行托架的刚强度校核和射击精度影响分析。并根据仿真结果,采用拓扑优化结合参数化建模方法对托架进行结构优化[8-9],有效提高了车载机枪行进间射击时的精度和稳定性。

1 基本理论

1.1 路面不平度理论

战车在作战时一般行驶于未铺装的路面,行进时会受到由于路面起伏引起的随机振动,导致机枪托架受到随机的振动激励[10]。车辆作为传递系统将路面不平度激励输入到机枪托架上。

将路面相对于基准平面的高度q,沿道路走向长度d的变化q(d)称为路面不平度,定义其功率谱密度为Gq(n)。按照国家标准GB/T7031—2005机械振动道路路面谱数据,将道路等级分为8级,由于装甲车、突击车多为野外作战,故选择标准中的D级路面,包括砂石铺筑的简易路面及压实的未铺装路面等[10],此时路面不平度位移功率谱密度表示为:

式中:n为空间频率,m-1;n0为参考空间频率,取值为0.1 m-1;Gq(n0)为路面不平度系数,由国家路面等级分类给出;w为频率指数,取值为2。

式中:f为时间频率,f=un;u为车速[11]。

通过谐波叠加法[12]可以得到路面垂直加速度a随时间变化图像如图1所示。

图1 路面垂直加速度时域曲线

1.2 发射动力学理论

托架除了承受行进间由于路面不平度引起的振动外,在实际作战时,还会承受由机枪连续射击引起的后坐冲击,此冲击为强冲击,会对托架的结构刚强度有较大影响。

机枪射击引起的后坐力主要由弹药的内弹道过程产生的反作用力引起,根据某12.7 mm机枪射击过程中的物理化学变化,结合内弹道的基本假设,建立内弹道期间的数学方程,计算得到膛内火药气体压力随时间变化的情况。

假设机枪在射击过程中,机枪整体受到的后坐力Ff与膛底压力Ft相等,即:

Ff=Ft=pS

(4)

式中:p为膛内平均压力;S为膛底截面积。

在机枪连续射击时,后坐力随弹丸击发而重复,设机枪射频为600发/min,则当机枪连续射击10发时,后坐力变化曲线如图2所示。

图2 10发连射后坐力曲线

2 行进间发射模型

行进间发射动力学模型是为了分析车载武器在路面不平度输入以及射击载荷同时作用下的动力学响应[13],分析时,将整个车载机枪系统简化为车辆和机枪2个部分,2个部分由托架连接,托架模型简图如图3所示。

图3 托架示意图

车辆系统由轮胎、悬架、车体框架等结构组成,由于托架固有频率远离轮胎等结构的固有频率,在进行车辆垂直振动分析时,将车辆系统简化成单自由度振动系统。

机枪系统由多个零部件及运动机构组成,内含机框、身管、机匣、枪托、枪管簧、复进簧等弹性构件,运动情况复杂;为了简化模型并放大工况,将整个机枪发射系统简化为一个质量为18.5 kg的枪体,枪体后坐力主要来自膛底气压对内膛截面的作用力。机枪与托架之间有缓冲装置,装有缓冲装置的滑板底座固连于托架上,缓冲装置另一端直接连接枪体。简化后的行进间发射模型如图4所示。

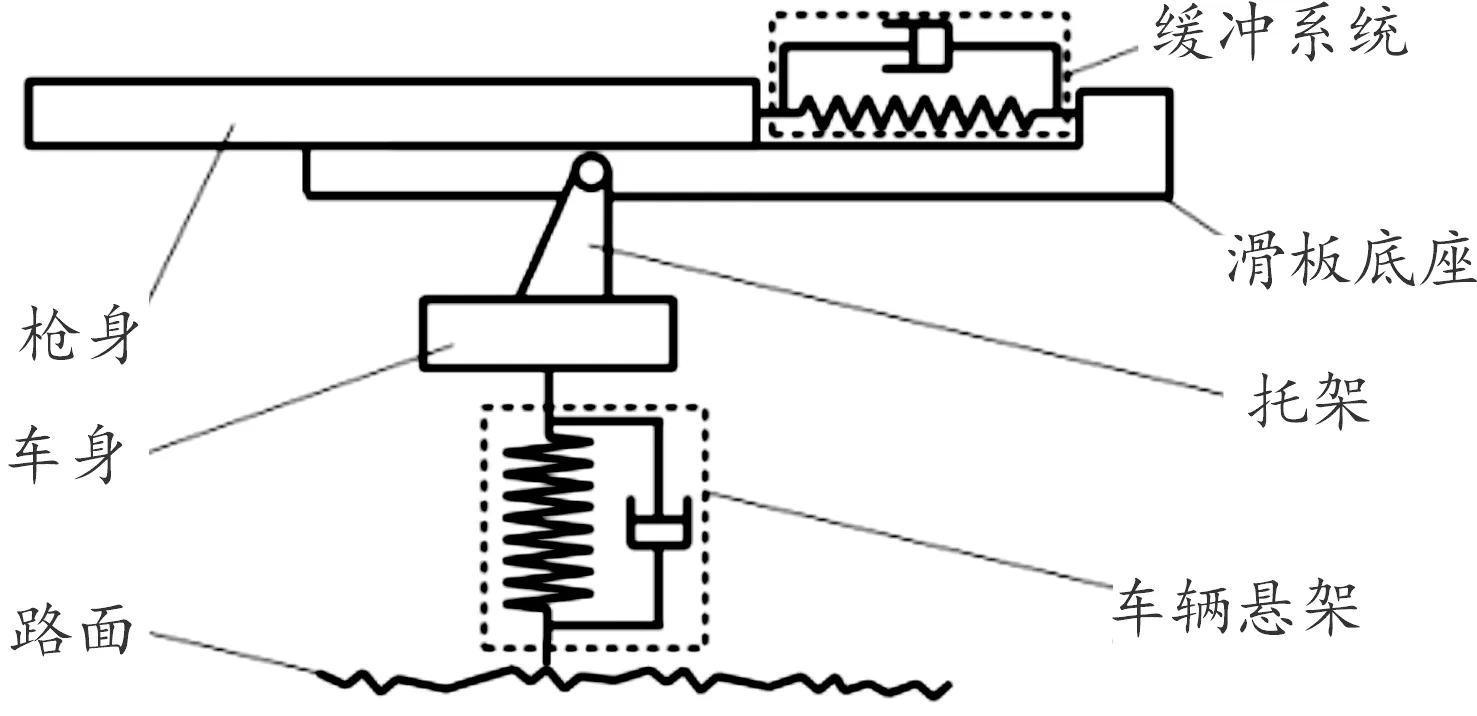
图4 行进间发射模型图

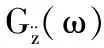
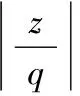
式中:ζ为系统的阻尼比,取0.25;λ为频率比。

最终得到车辆系统的加速度输出,即托架受到的加速度激励的功率谱密度曲线如图5所示。

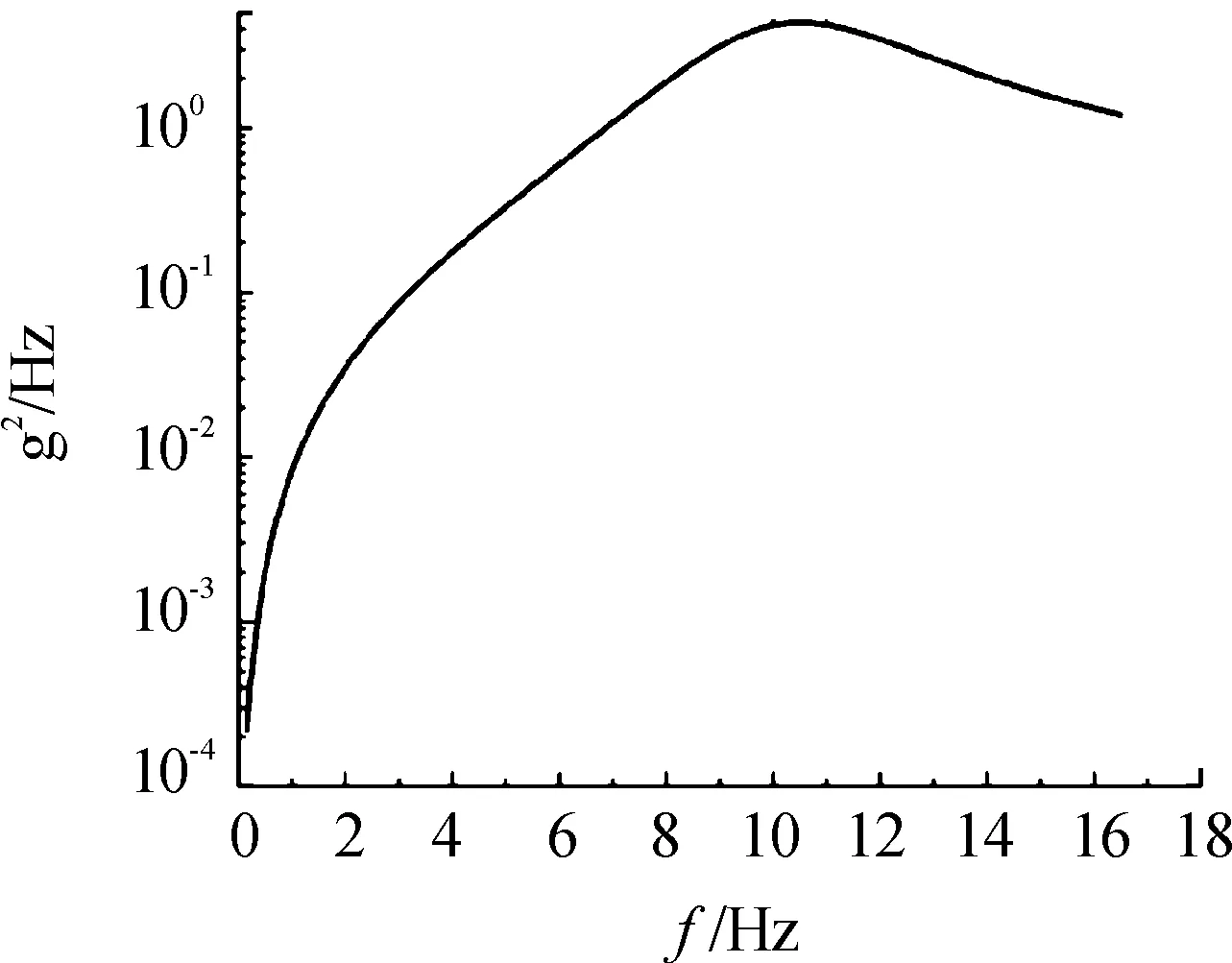
图5 PSD曲线

对于机枪,取滑板为惯性参考系,可以得到系统的运动微分方程为:

式中:F为滑板受到的后坐力;m为枪身质量;c、k分别为缓冲系统的弹性系数和阻尼系数;x为枪身位移。

将枪身在10发连射时的后坐冲击Ff作为输入,得到了滑板(即托架)受到的冲击力曲线如图6所示。

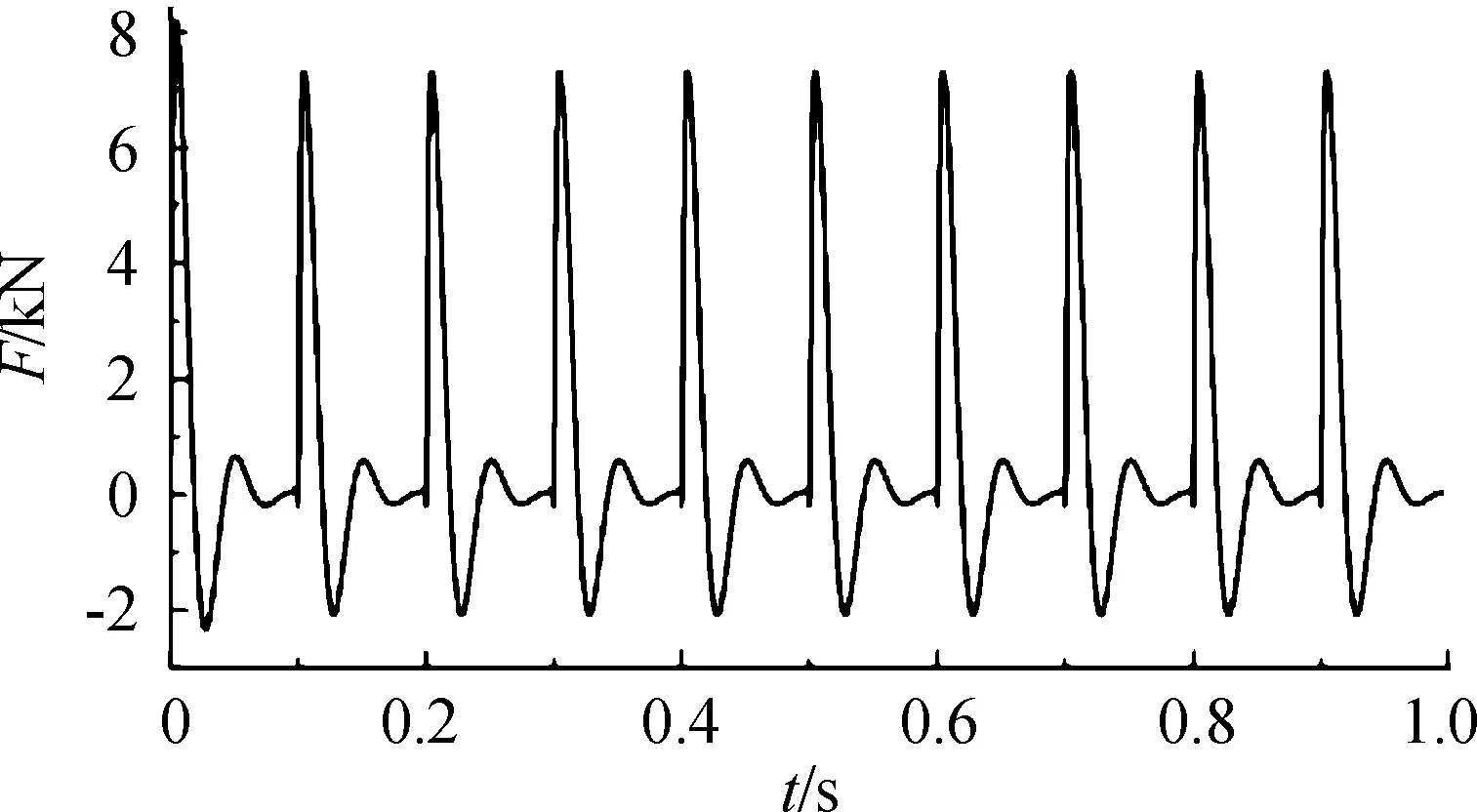
图6 滑块后坐力曲线

唐俊智[14]在某遥控武器站结构设计时,将车载机枪架座安装在固定平台上,进行3～5发点射,实验得到固定枪架上的后坐力为8 000 N;由图6可知,数值模拟出现最大后坐冲击力为8 194 N,与实验数据差别不大,故数值模拟的数据具有可靠性。

3 仿真分析

3.1 假设

在对托架进行仿真分析时,做出如下假设:

1) 机枪与托架之间的滑板为刚体,在射击时不会产生变形。

2) 托架与车辆之间为刚性连接,车辆的振动响应直接作用于机枪。

3) 高低机的大小齿弧均为刚体,且二者完全啮合,能够完全传递力。

4) 机枪质心与托架耳轴连线与身管平行。

此时,以托架耳轴中心为原点,建立oxy坐标系,x轴正向指向枪口方向,y轴向上为正,对托架的受力分析如图7所示。

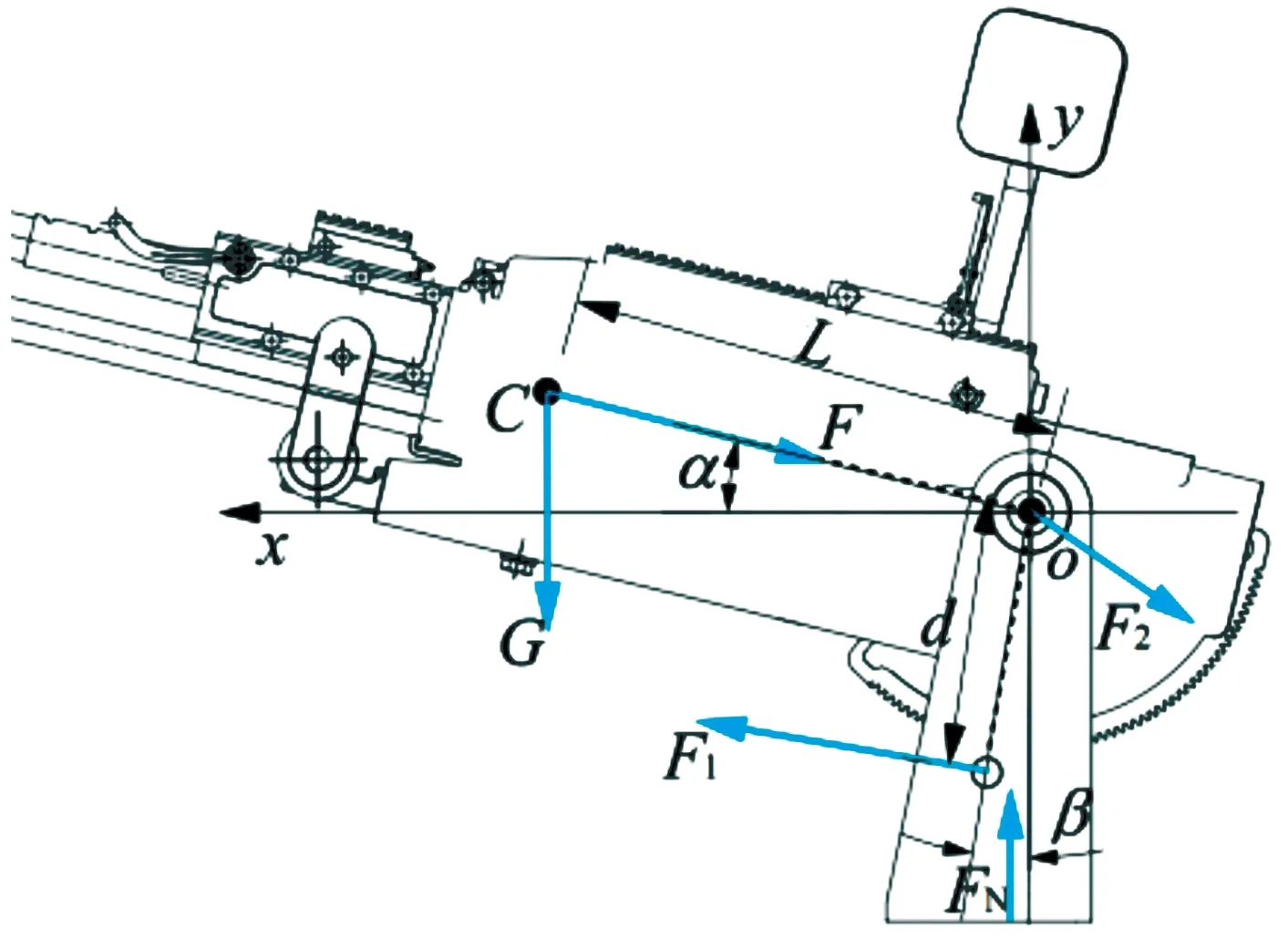
图7 受力分析图

图7中,α为托架耳轴中心与机枪质心连线与x轴夹角;β为高低机两齿轮中心连线与y轴的夹角;L为机枪质心C与耳轴中心o的距离;d为高低机两齿轮中心距;G为枪身和滑板的等效质量;F为后坐冲击力;F1为高低机手轮与托架之间的作用力;F2为机枪对托架的压力;FN为车辆对托架的支持力。

由图7可得:

式中:m为托架质量,值为9.86 kg;M为系统总质量,值为34 kg;a(t)托架车辆输出的加速度;g为重力加速度,取值 9.8 m/s2。

3.2 力学仿真

在ANSYS仿真软件中,对托架进行受力仿真分析,得到在3种射角下10发连射过程中托架应力σ、变形δ随时间的变化曲线如图8、图9所示。

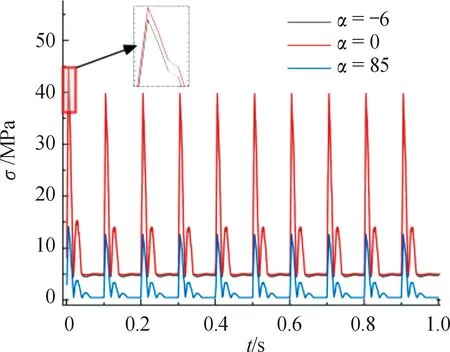
图8 应力变化曲线

图9 变形变化曲线

由图8、图9可知,射角为-6°和0°时的应力和变形基本一致,射角为85°时的应力和变形相对较小,应力及变形的变化规律与机枪后坐力变化情况相似,所以托架变形主要受到的是机枪后座力的影响。最大应力及变形结果如表1所示。

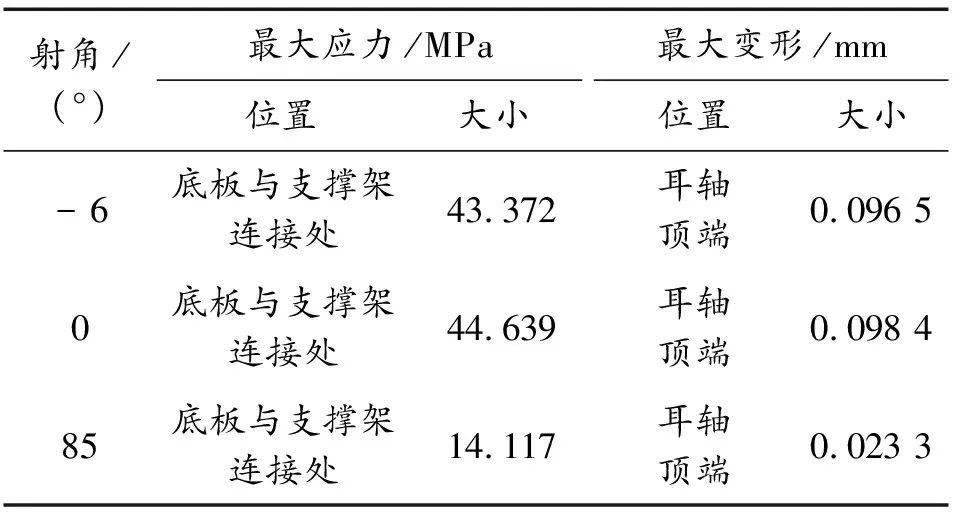
表1 最大应力变形

材料选用结构钢,其屈服强度σs为235 MPa,由于托架本体最小安全系数为2[15],故许用应力[σ]取117.5 MPa。由表1知,在机枪射击10发的过程中,满足刚强度要求。3种射角对比下,平射时托架工况最为恶劣,此时的最大应力、变形云图如图10、图11所示。

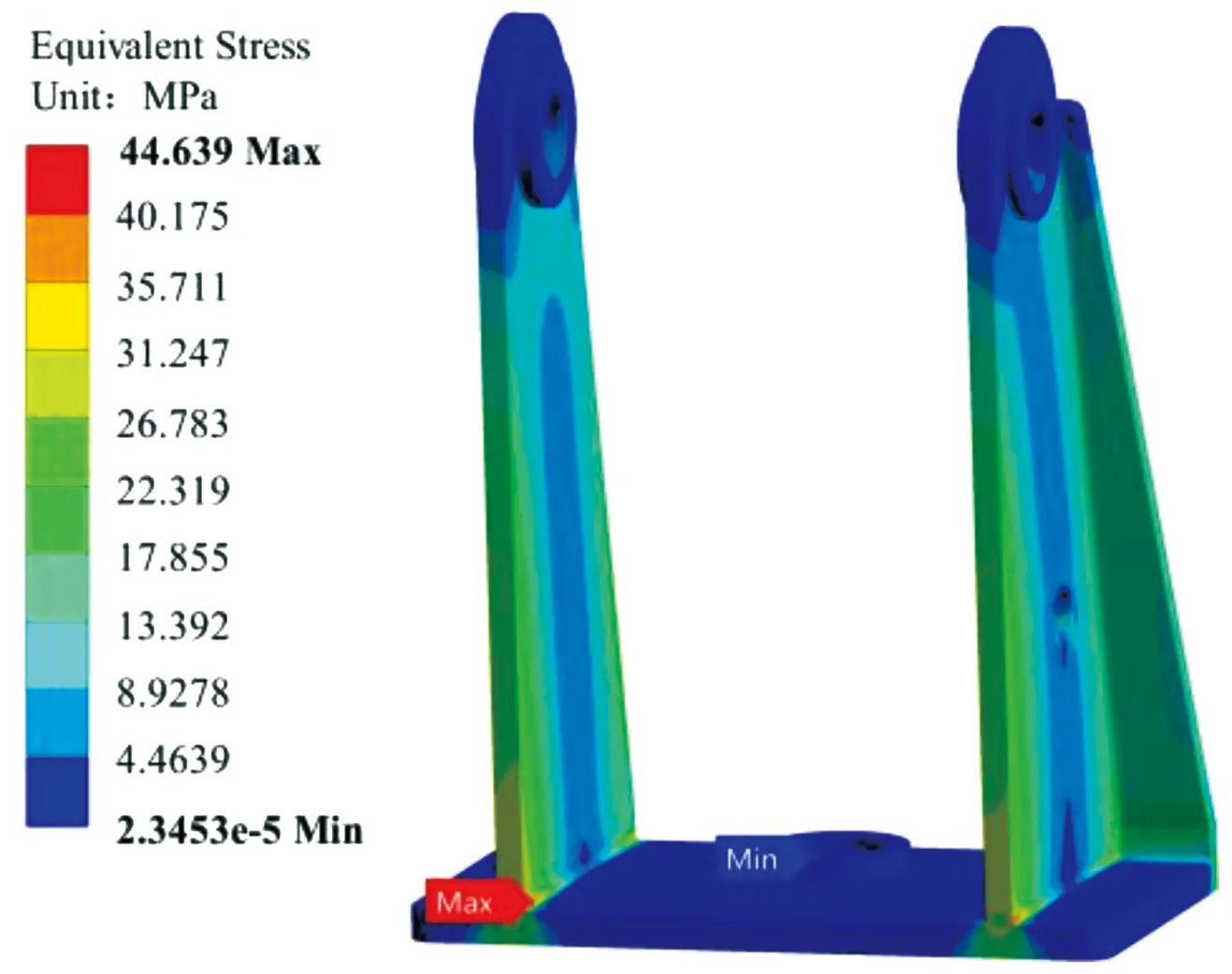
图10 应力分布云图

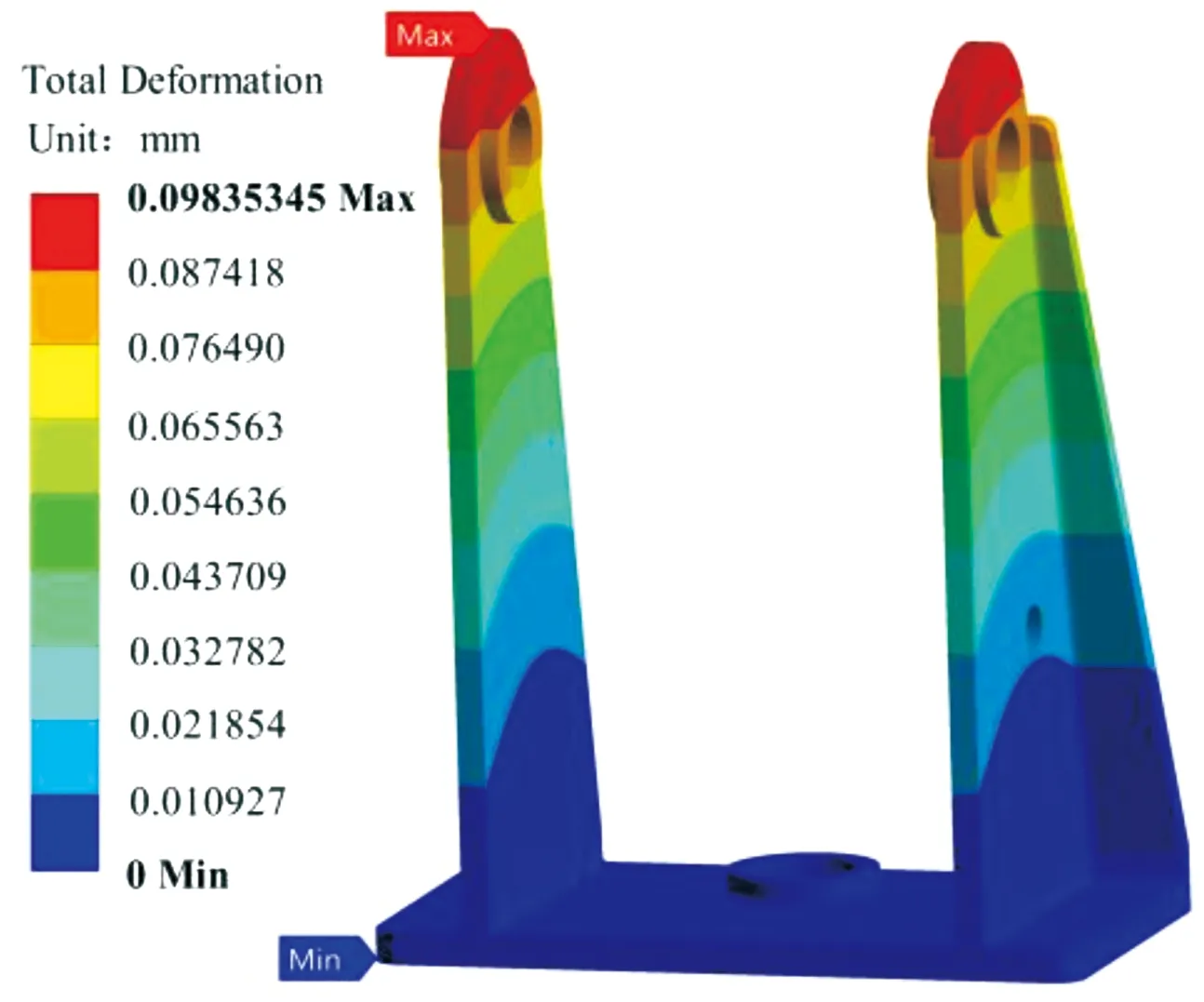
图11 变形分布云图

由图10、图11可知,在机枪平射10发的过程中应力最大点出现在托架底板与支撑架连接处,该部位是保证结构可靠性的关键部位。该部位出现的最大应力不超过44.639 MPa,离许用应力差距较大,在持续射击下不会出现低周疲劳,满足使用要求。

最大变形出现在耳轴顶端,耳轴直接与机枪相连接,由于高低机的存在,两边耳轴的变形并不对称,两耳轴会产生一个交错变形,该变形会使机枪产生水平方向上的偏角θ,从而引起射击误差。托架变形示意图如图12所示。

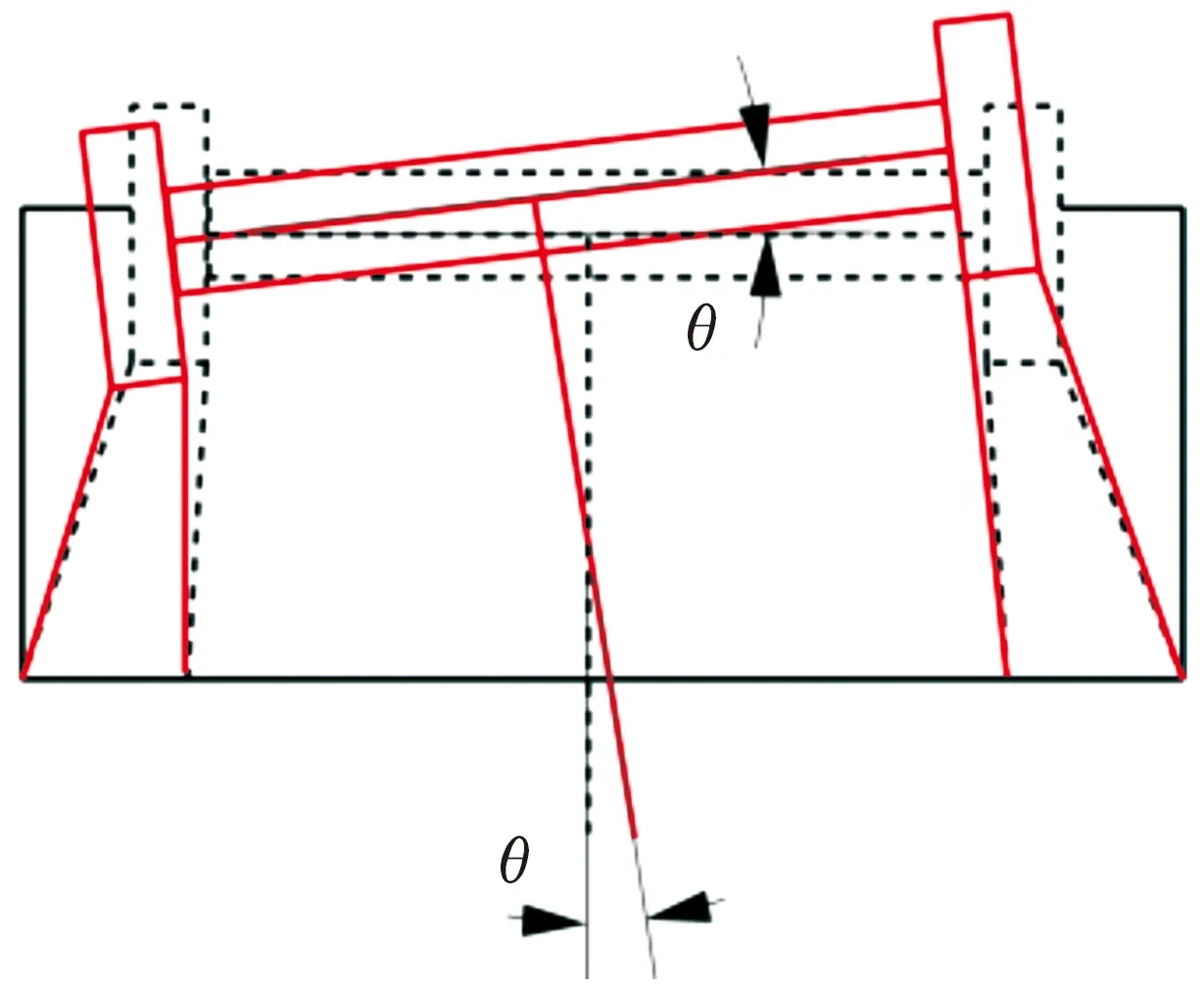
图12 托架变形示意图

式中:δ1,δ2分别为托架两支撑板的最大变形量;l为两耳轴之间的距离。

由ANSYS变形结果可以得到行进间10发连射时由托架变形引起的枪口偏角曲线如图13所示。

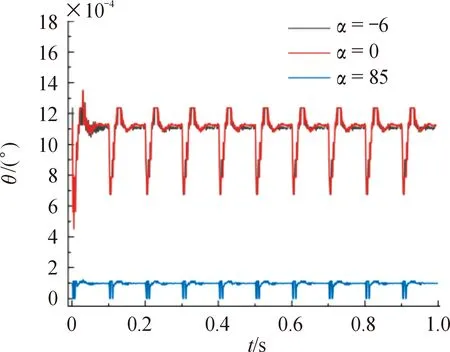
图13 枪口偏角变化曲线

以有效射程为1 500 m计算,可计算得到3种工况下的最大枪口偏角和目标位置的射击误差Δ如表2所示。

表2 最大射击误差表

由图13可知,平射与射角为-6°时,枪口偏角相对较大,变化情况基本一致,射角为85°时偏角最小;枪口存在最大偏角为0.001 35°,出现时间为一次击发完成后,但是由于枪身自重和车身垂直加速度的存在,枪口在弹丸离枪后会一直有一个0.001 11°的偏角;因为将枪体视为刚体,所以枪口偏移量主要是由于偏角的存在而形成的,其变化趋势与枪口偏角一致,最大偏移量为0.011 3 mm。

4 结构优化设计

由仿真结果云图可知托架部分结构的应力很小,存在较大冗余量,可以通过拓扑优化的方法对这部分结构进行重新设计。拓扑优化就是在给定的设计域里面,寻找到满足边界约束的最优结构分布[16],此处运用ANSYS Workbench的拓扑优化模块进行优化设计,该模块基于变密度法对托架结构进行优化。

变密度拓扑优化方法是基于有限元方法的一种结构优化方法,在有限元方法的基础上,将每个离散的单元定义为独立变量,该变量记为单元的相对密度,即伪密度设计变量。伪密度为0(或接近0)表示对应的单元处无实体,去除该部分材料;伪密度为1(或接近1)则表示对应的单元处为实体,保留该处的材料[17-18]。

变密度法通过伪密度的变化控制单元刚度的变化,进而调整结构总体刚度矩阵的变化,在给定约束下进行计算,经过优化使托架的结构刚度达到最佳,材料分布达到最优[19]。

本文中将2块支撑板作为设计域进行拓扑优化,为了保证托架在任意工况下都能满足强度使用要求,选取平射作为仿真工况,并取取安全系数为2[15],故许用应力[σ]取117.5 MPa,为了减少构冗余质量,保留60%的质量。经过28次迭代计算后得到图14(a)所示的拓扑优化构型,根据优化结果进行部分结构重新设计,保留主传力路径,对较厚的支撑板进行减厚处理,去除冗余质量。

图14 结构优化简图Fig.14 Structure optimization brief diagram

由于高低机及平衡机的存在,使得2支撑板受力并不对称,导致两耳轴在连续发射过程中会产生交错变形,形成射击偏差。为减少该交错变形,需要对2支撑板进行分别设计,保证行进间射击工况下的刚度匹配,减小这部分射击偏差。

在拓扑重构的托架模型基础上,为了实现对2支撑板刚度进行分别控制、提高仿真运算效率,以右支撑板减去部分(图14(b)深色部分)的深度c作为设计变量,使用UG联合ANSYS Workbench进行参数化建模仿真[19]。在UG建模时定义拉伸深度为变量,其值定义范围为[2,4],以平射工况作为对比条件,对比不同深度的力学性能响应,得到托架力学性能变化曲线如图15所示。

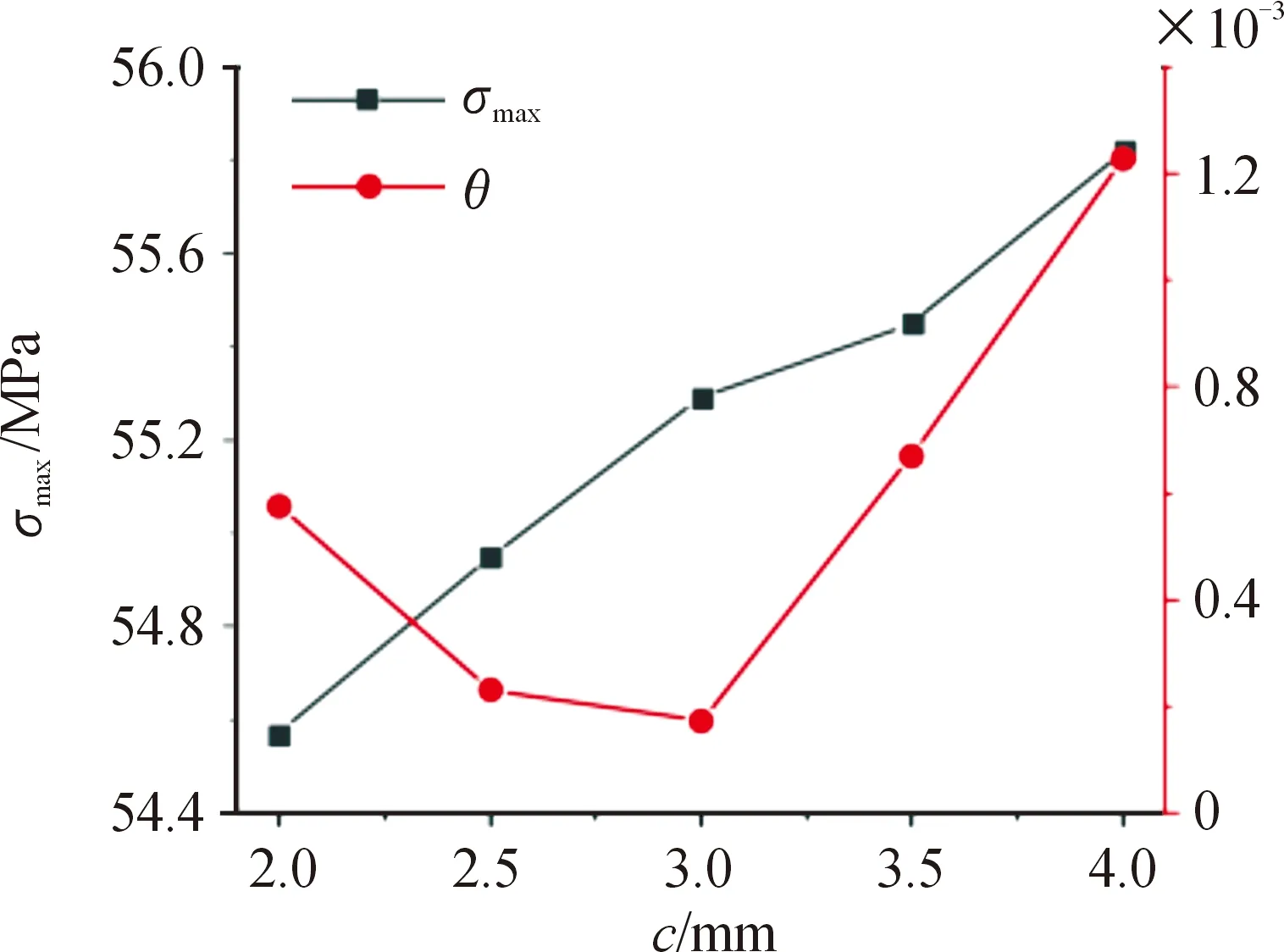
图15 力学性能变化曲线

由图15可知,当减去深度为3 mm时,优化效果最好,以此作为最终优化结构,得到相关参数如表3所示。

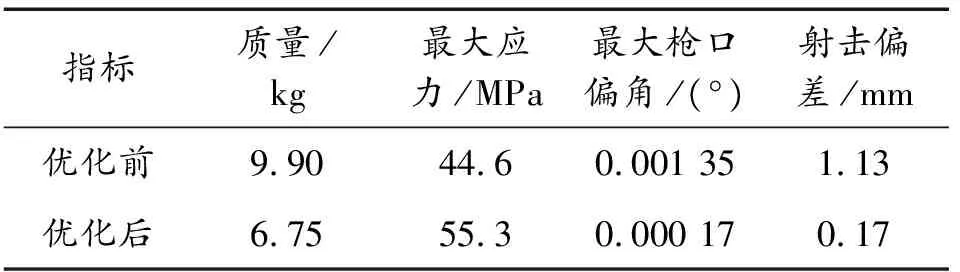
表3 优化前后参数对比

由表3可知,优化托架结构后,托架质量降低了31.82%;支撑板刚度匹配性得到改善,由托架变形引起的射击偏差减小至0.17mm,对射击基本没有影响,最大应力较原结构有一定幅度的上升,但远小于许用应力,不存在低周疲劳及强度失效的情况,依然满足强度条件。

托架经过优化后,极大降低结构质量,在满足使用强度要求的同时,还能够有效提高托架支撑板的刚度匹配性,从而减小行进间射击时由托架变形导致的射击偏差。优化后托架的结构变形,基本不会影响机枪正常工作。

5 结论

本文通过建立行进间发射动力学模型,得到托架的受力情况,对托架进行有限元仿真,得到3种工况下托架的力学性能和对机枪射击精度的影响,通过拓扑分析优化,对托架的支撑板进行重新设计,利用参数化建模的方法,提高2支撑板的刚度匹配性,使支撑板的交错变形得到有效控制,从而减小射击偏差。主要结论如下:

1) 在2种激励同时作用下,平射时的工况最为恶劣;托架所受到的最大应力位于底板与支撑架连接处,大小为44.639 MPa,远小于许用应力,满足强度要求;最大变形量为0.098 4 mm在材料的弹性变形范围内,满足刚度要求。

2) 最大应力的变化规律与机枪后坐力变化情况相似,即机枪的后坐冲击为托架所受力的主要部分。

3) 通过拓扑优化结合参数建模仿真分析的方法对托架进行结构重新设计,减小托架在行进间射击过程中的交错变形。结构优化后,满足结构强度的同时,结构质量减小31.82%,托架耳轴变形最大会引起枪口会产生0.000 17°的枪口偏角;换算到目标位置,最大会产生0.17 mm的射击偏差;优化后的托架变形引起的射击误差,基本不会影响机枪正常工作,可以为车载机枪及遥控武器战设计提供有效参考。