内置不同角钢骨架的型钢混凝土梁受力性能研究*
2023-08-03韩博文高华国尤季旺王庆利
韩博文, 高华国,2,3, 尤季旺, 赵 畅, 王庆利
(1 辽宁科技大学土木工程学院,鞍山 114051;2 中国地震局工程力学研究所,哈尔滨 150080;3 中国地震局地震工程与工程振动重点实验室,哈尔滨 150080)
0 引言
型钢混凝土(steel reinforced concrete,SRC)结构是钢-混凝土组合结构中的一种重要形式,因其较好的承载能力、优良的延性及耗能能力等因素,被广泛应用于大跨重载结构和高层乃至超高层建筑中[1-3]。但正因为针对型钢混凝土组合结构的研究日趋成熟,提出新的型钢和混凝土的组合形式以达到更高的承载力要求也成为目前研究的主要方向。
通过结合型钢及混凝土两种材料的优势,众多国内外学者开展了大量型钢混凝土构件的试验研究。其中杨勇[4-6]提出部分预制型钢混凝土梁,分别进行了7组梁受弯性能和17组梁受剪性能静力试验,结果表明该试件的现浇和部预制分能够很好地协同工作;张令心[7]将型钢混凝土根据核心区混凝土的约束效应分为三个区域,并给出了基于柔度法的有限元模型。童乐为[8]开展了型钢混凝土梁在低周往复荷载作用下的疲劳试验,并提出应力幅-疲劳寿命曲线;苏益声[9]提出一种蜂窝式的型钢组合梁,并对其静载受力性能进行了试验研究,探究了这种新型构件截面对抗弯刚度及承载力的影响;朱筱俊[10]针对H型钢混凝土梁开展了受扭性能试验,结果表明型钢在试件开裂后对裂缝的发展起到了良好的控制作用;上述研究多为探究型钢的不同构造对组合梁受力性能的影响,型钢混凝土梁在其他影响因素作用下,也可能产生不同的受力性能,用于多种实际建筑工程中。
为了研究型钢混凝土的更多可能性,王连广[11-12]分别设计了两组空腹式型钢混凝土梁进行受弯试验,其中一组为无粘结预应力SRC梁和一组非预应力SRC梁,结果表明施加预应力的构件裂缝出现较为滞后,且后续发展缓慢;陈宗平等[13-14]提出一种高温型钢-再生混凝土组合梁,分析了温度等变化因素对组合梁自身力学性能的直接影响,并通过推导得到相应的最大极限承载力的计算公式;Alhozaimy[15-16]研究了不同氧浓度对不同定义条件下混凝土中嵌入的钢筋的被动膜形成和腐蚀的时间依赖性影响;代金亮[17]设计了一种空间钢骨架-混凝土梁并针对其受弯性能开展一系列对比试验;王兵等[18-19]采用有限元软件建立了高温后型钢再生混凝土梁受弯的有限元模型,并对其破坏模态进行机理分析。
据此笔者提出四种新型内置不同角钢骨架的型钢混凝土梁(steel reinforced concrete beam with built-in different angle steel framework,简称ARCB)。考虑到ARCB中空间角钢骨架与混凝土之间的滑移问题,在角钢上设置一定数量的钻尾螺栓作抗剪连接件,使混凝土与角钢骨架能够良好的协同工作。为了进一步减少ARCB的自重,ARCB的空间骨架中部减少缀板连接件和箍筋的数量,形成一种空腹式空间角钢骨架。
由于ARCB与普通钢筋混凝土梁(SRCB)相比,用角钢代替受压区和受拉区钢筋、用型钢缀板代替箍筋致使组合结构发生变化和角钢不同的放置位置、放置方式的问题,故需要对其相应的破坏机理以及承载力计算方法进行研究。ARCB中由于钢筋骨架中部未设置缀板连接件和箍筋,会在一定程度上影响结构的承载能力,因此需要对其受力性能进行深入研究。基于此,课题组设计四种不同的ARCB试件对梁的受力性能开展试验研究,并提出相应的刚度及承载力计算方法。本文中介绍四种ARCB试件的理论计算、试验研究以及有限元模拟结果,以期为相关工程应用提供参考。
1 试验概况
1.1 试验设计
试验共设计了10个试件,包括5种截面类型的梁,不同截面类型的梁依据fy(拉应力设计值)×As(钢筋截面面积)值相等进行配筋。10个试件均为2800mm×200mm×300mm的矩形截面梁,其保护层的厚度为30mm。各试件中的角钢和缀条均采用Q235轧制型钢,其中ARCB-3和ARCB-4构件中的角钢与缀板均通过焊接连接。试验组RCB-0、ARCB-1、ARCB-2中的纵筋为直径14mm的HRB335级钢筋,箍筋为直径8mm的HPB300级钢筋。为避免钢骨架与混凝土之间产生相对滑移现象,使钢骨架与混凝土协同工作,制作试件时在角钢双肢每隔一组箍筋(缀条)设置一组六角钻尾螺栓12#×30以作抗剪连接件的作用,如图1所示。各试件的截面形式及尺寸见图2。

图1 抗剪连接件

图2 截面尺寸
所有试件均采用同一类型的型钢和混凝土,其中混凝土的强度等级为C30,制作试件的同时预制8个混凝土立方体试块,并与试验梁在相同环境下进行养护,经过28d后对试块进行抗压强度试验,混凝土实测立方体抗压强度分别为33、31、30、28、32、27、32、30MPa,其余试件参数见表1、2。

表2 钢材拉拔件实测参数平均值
1.2 加载装置及加载方案
试验采用50t电液伺服压力试验机在梁试件跨中通过分配梁施加集中力荷载,采用逐级加载的加载制度,每5kN作为一个等级。为避免在加载过程中受压区混凝土产生应力集中而发生局部破坏,同时,在两个加载点下分别放置一块130mm×80mm×7mm的Q235钢板做垫片。通过XL2101B6静态应变仪采集钢筋、角钢、混凝土的应变和试件的竖向荷载、位移。当试件受拉区形成贯通裂缝、试验机自动卸载或跨中挠度超限时,即认为试件已破坏。
2 ARCB梁受弯性能试验结果及分析
2.1 试件破坏形态分析
从整个试验过程来看,各个试件均表现为明显的正截面弯曲破坏,试件的破坏形式如图3所示。

图3 试件破坏形式
对于RCB构件,在加载过程中梁底部跨中受拉区混凝土率先达到极限抗拉强度退出工作,继续加载,受拉区的纵向受力钢筋逐渐进入屈服状态,随后受压区混凝土达到极限抗压强度。试件ARCB的加载过程中,试件底部跨中受拉区混凝土首先达到极限抗拉强度,该过程相较于RCB构件所用的时间有所延长,随后开始逐渐发生裂缝,5组试验梁均发生弯曲破坏。
2.2 荷载-挠度曲线及破坏机理分析
从试件的破坏形态上看,ARCB与RCB试件表现出相似的受力过程,试件跨中位置的荷载-挠度曲线见图4。在加载初期曲线为直线段,试件达到开裂荷载前始终处于弹性工作阶段,随后图中曲线进入曲线段,试件开始进入弹塑性阶段,但这一阶段的持续时间较短,当受拉区的钢材达到屈服应力后,试件抗拉能力急剧下降,挠度增长速度加快,刚度随之减小,最后试件达到极限荷载发生破坏。

图4 荷载-挠度曲线
对比5组试件得出,在同等力的效应作用下内置角钢空间骨架的型钢混凝土梁具有较大的刚度,型钢与混凝土协同作用效果更好;角钢肢尖相对比肢背相对的布置方式对混凝土的约束更强;肢尖相对布置的空间角钢骨架对核心区混凝土的约束作用更为良好。
对比四组ARCB试件可知,相同Asfy值的试件,由缀条代替箍筋对核心混凝土的约束效应更好,其承载力和刚度的提升效果也较为明显。达到峰值荷载时ARCB试件仍能够维持较高的承载能力和变形能力。各个构件的极限荷载及破坏形态见表3。

表3 试件极限荷载及破坏形态
由表3可知,所有不同布置形式的ARCB试件均在一定程度上提高了自身极限荷载。其中类工字形角钢骨架所在的试验组4极限荷载较RCB-0构件提升约21.5%;ARCB-1试件极限荷载增幅25%,而对核心区混凝土约束效应最强的ARCB-3构件其极限承载力相较于ARCB-1构件提升了8.5%。
2.3 裂缝形态分析
各试件的裂缝形态如图5所示。由于本试验为了避免加载过程中产生应力集中现象,采用分配梁进行加载,裂缝基本先发生在纯弯段,随着加载继续进行,纯弯段裂缝不断增加随后趋于稳定,剪跨段逐渐由细小裂纹发展为指向加载点的斜裂缝,直至构件破坏。
根据图5对比发现,试验组3的裂缝宽度比类工字形的角钢骨架所在的试验组4更均匀;ARCB-2和ARCB-3两组试件产生的裂缝宽度较小,说明角钢肢尖相对布置的试件抗裂性能相较于其他试件较好,且剪跨段裂缝较少,基本为纯弯曲破坏。
2.4 M-Ф关系曲线
曲率Ф计算简图如图6,其几何关系公式为:

图6 曲率计算简图
将试验数据带入式(1)得出各个试验梁的曲率值,并绘制弯矩曲率(M-Φ)曲线,见图7。由图7可知,加载前期曲线整体呈线性变化,直至受拉区混凝土达到极限抗拉强度发生裂缝,中和轴上移,试件的刚度开始降低,随后受拉区角钢进入屈服阶段,弯矩增幅缓慢而曲率增长速度加快,曲线逐渐趋于水平。ARCB-2试件和ARCB-3试件因其角钢布置方式为肢尖相对,在M-Ф曲线中与水平坐标轴围成的面积普遍大于其余组试件,延性较好;对比ARCB-1、ARCB-4试件和ARCB-2、ARCB-3试件可知,由于缀条比箍筋与混凝土的接触面积更大,对试件核心区混凝土的约束效应更强;受拉区和受压区同时布置角钢时延性更好。
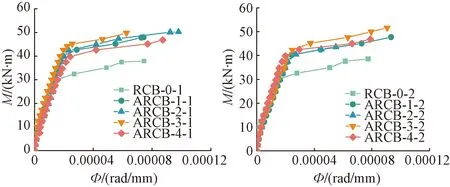
图7 M-Ф关系曲线
2.5 应变分析
2.5.1 混凝土截面应变分析
试验通过XL2101B6静态应变仪采集混凝土梁跨中40、150、260mm三种不同截面高度的应变,图8为跨中截面应变分布图,通过观察不同荷载下纯弯段混凝土应变随截面高度的变化规律可知:各构件混凝土截面应变基本符合平截面假定。

图8 跨中截面应变分布
2.5.2 钢筋及角钢应变分析
提取编号为1的试件中受拉区跨中钢筋/角钢水平一肢的应变,绘制试验荷载与角钢应变关系曲线,如图9所示。相同荷载下,RCB试件中钢筋的应变值比ARCB试件中角钢的应变值大很多,其中,受拉区和受压区均布置角钢且肢尖相对布置的试件ARCB-3的承载力更高,其极限荷载较RCB试件提升约46%,较受压区布置受力钢筋、受压区角钢肢尖相对布置的试件ARCB-2提升约12%,较受压区受拉区同时布置角钢但肢背相对的试件ARCB-4提升约7%。相同荷载作用下的应变比RCB试件减小了95.2%。

图9 荷载-应变曲线
试验结束后,从采集到的角钢上所布置的应变片的数据可以看出,纯弯段受力钢筋和角钢在破坏时均已达到屈服状态;将试验梁进行切割后发现空间钢骨架与混凝土之间并未存在明显的滑移痕迹,这也进一步说明ARCB构件具有良好的整体性。
3 有限元模拟
3.1 单元选取及材料本构
混凝土梁构件、角钢、缀条、刚性垫片均采用实体单元(C3D8R),梁中受力钢筋、箍筋均采用桁架单元(T3D2)。混凝土的本构模型采用ABAQUS中自带的CDP模型,受力钢筋、角钢和箍筋均采用理想弹塑性模型,材料参数见表4、5。

表4 钢材材料参数

表5 混凝土材料参数
3.2 边界条件及加载方式
为了模拟简支梁真实的受力情况,在梁底部梁端分别绑定80mm×130mm×7mm的刚性垫片,限制一侧刚性垫片X、Y、Z向的平移自由度和另一侧刚性垫片X、Y向的平移自由度。空间钢骨架通过绑定(Tie)连接并内置于混凝土构件中,保护层厚度为30mm。梁顶部刚性垫片按照试验中剪跨比为3的分配梁位置进行布置,与混凝土梁通过绑定命令连接,在刚性垫片上表面的中心设置两个参考点RP-1和RP-2,分别与垫片上表面耦合,在两个参考点施加Y轴负方向的位移荷载。
3.3 网格划分
按照内置角钢空间骨架的型钢混凝土梁的构造特点和具体尺寸,对于网格尺寸,混凝土单元选用50mm,角钢、缀条、受力钢筋和箍筋均选用30mm,刚性垫片选用50mm。试验梁的网格划分如图10所示。
图10 网格划分示意
3.4 模拟曲线结果
图11(a)~(e)为全部试件的试验和模拟结果曲线对比,总体来看,两者的吻合情况较好,在加载初期的弹性阶段范围内,两者的曲线斜率几乎一致,说明有限元模拟很好地预测了试件弹性范围内的刚度变化。图11(f)为5组试件有限元模拟汇总,从图中可以看出,在荷载达到20kN时,5组试件的斜率均发生一定变化,说明试件在该位置处发生刚度折减。图12为试件ARCB-3的刚度折减点应力云图,可以表征刚度折减时刻构件的细观应力状态,该时刻的挠度为1.02mm,此时受拉区混凝土已经达到极限抗拉强度开始进入下降段,应力为1.66MPa,该时刻角钢应力为98MPa,未达到其屈服应力,试件仍处于线弹性阶段;当挠度达到5.1mm时角钢达到屈服应力,此时荷载达到极限荷载的45%;继续加载,试件挠度增长速度加快而承载力提升速率变缓,直至角钢达到极限应力的96%时,试件开始发生破坏,退出工作。

图11 模拟曲线对比

图12 刚度折减点应力云图
3.5 破坏模态
以前文中总体性能较好的ARCB-3试件为例,图13中(a)为其有限元模拟的破坏形态,图(b)为ARCB-3-2试件的试验照片。两者变形规律基本一致且都为弯曲破坏,跨中受拉区纯弯段破坏较为明显,表现为多条贯通裂缝以及大量均匀微小裂缝,模拟结果与试验较为一致。
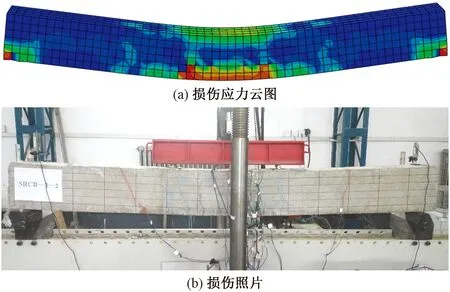
图13 混凝土损伤
图14为ARCB-3钢-混凝土组合梁挠度分布曲线。给出了ARCB-3试件有限元模型在不同受力阶段下的挠度沿梁全跨方向的分布状态(L为试件的跨度),从图中可以看出,型钢-混凝土组合梁的挠曲变形大致基于组合梁跨中点呈对称分布。

图14 挠度分布曲线
3.6 参数分析
为探究内置角钢空间骨架的型钢混凝土梁受力性能的影响因素,通过有限元模拟对其进行参数化分析,结果见图15,其中图15(a)、(c)以试验中承载力较好的ARCB-3试件展开分析,图15(b)对四组新型角钢骨架试件梁进行分析,图15(d)以带有受力钢筋骨架且承载力较好的试件ARCB-2为分析对象。
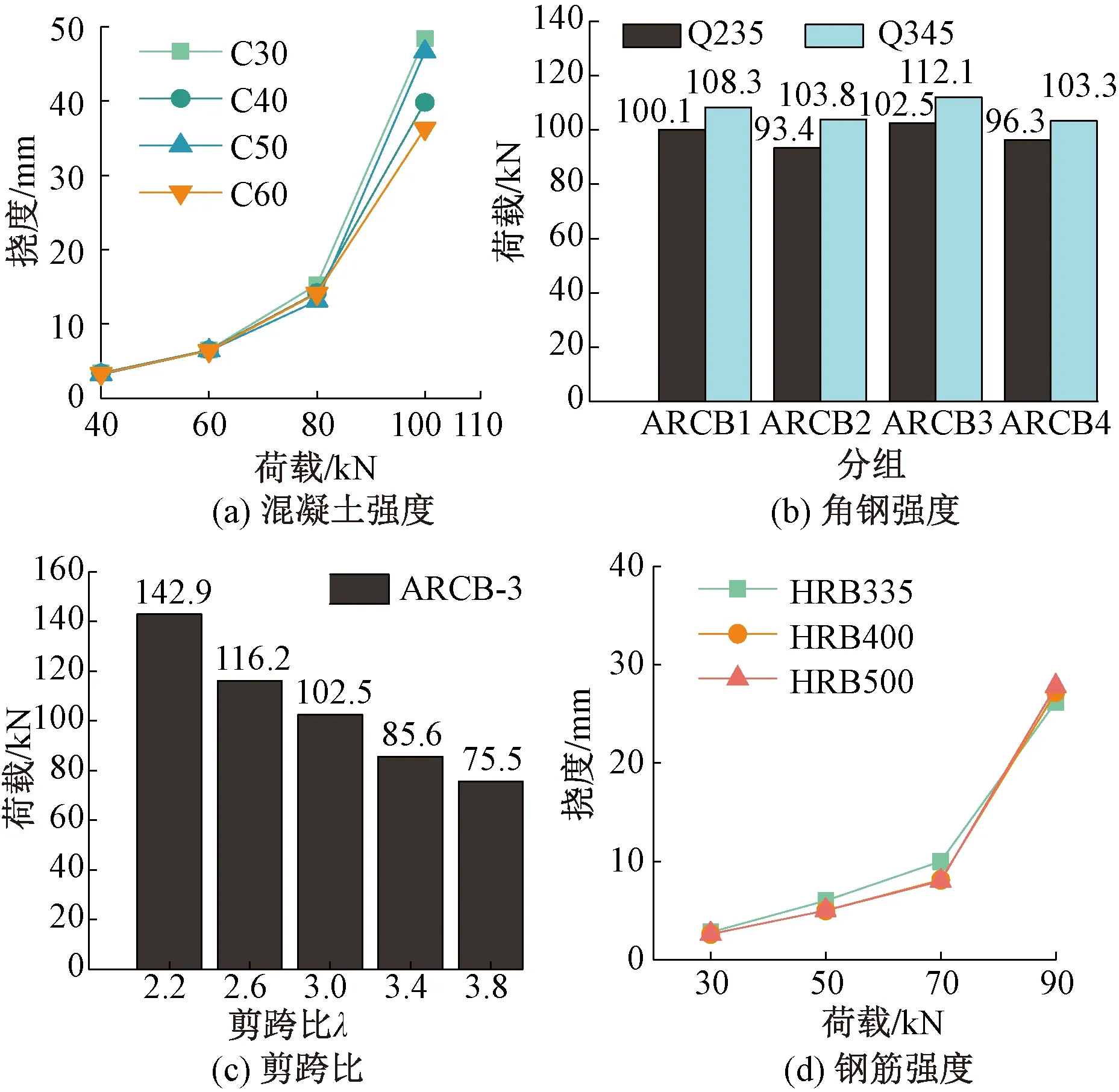
图15 不同参数下试件对比分析
图15(a)中混凝土强度等级分别为30、40、50、60MPa,分别提取40、60、80、100kN荷载下其挠度情况进行分析,发现加载前期各试件挠度基本相同,在接近构件极限荷载的100kN状态下时强度等级为C60的试件挠度比试验试件小33.3%,说明增大混凝土强度可是提升试件的刚度和抗弯性能;图15(b)中角钢强度等级为Q235~Q345,角钢强度等级的提高直接影响到试件承载力的大小,其中试件组ARCB2极限荷载提升最为明显,约11.1%,极限荷载提升幅度最小的试件组ARCB4也提升了7.3%;图15(c)中分析了不同剪跨比的影响,在一定范围内,试件的极限承载力会随着λ的增大而减小;图15(d)以带有受力钢筋骨架且承载力较好的试件ARCB-2为分析对象,钢筋强度等级分别为HRB335、HRB400和HRB500,加载前期挠度几乎一致,钢筋进入屈服阶段后钢筋强度等级越高的试件变形越小,加载后期挠度基本一致,说明提升钢筋强度等级对试件在一定荷载状态下抵抗变形能力有所助益。
4 正截面承载力及刚度计算
4.1 基本假定
1)型钢骨架与混凝土在试件破坏前协同工作;2)试件截面应变符合平截面假定;3)钢材的本构关系选用理想弹塑性模型,取极限拉应变为0.01;4)混凝土本构关系根据《混凝土结构设计规范》(GB 50010—2010)[20]选用。
4.2 正截面承载力计算
根据规范采用等效矩形应力图代替实际受压区混凝土应力图,如图16所示。

图16 等效矩形应力图
对受拉区角钢重心所在直线取矩Mu:

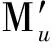

表6 理论值Mu与试验值对比
4.3 刚度计算
计算时,首先将角钢视为普通钢筋,如图17所示,得出受拉区角钢平均应力σsk的计算公式:
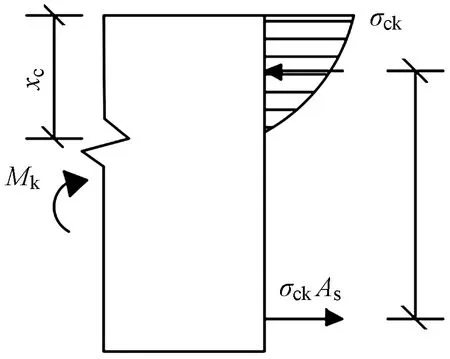
图17 截面应力图
式中:Mk为截面弯矩标准值;As为受拉区角钢截面积;η为内力臂系数。
受拉区角钢的平均应变εsk为:
式中Es为角钢弹性模量。
设不均匀系数为λ,则可推出角钢的平均应变εsa为:
对受拉区角钢重心所在直线取矩:
(6)
式中:ξ为相对受压区高度;εcm为受压区边缘混凝土平均应变;E0为初始弹性模量。

式中:ρ和ρ′分别为受拉区和受压区角钢的含钢率;Ec为混凝土的弹性模量;ζ为修正系数,其余参数含义见《混凝土结构设计规范》(GB50010—2010)。
截面短期抗弯刚度Bs可表示为:
结合文献[17,21]做出部分修改:
即可得出截面短期抗弯刚度Bs:
通过图乘法求得跨中挠度计算值f与试验值f′(选用每组编号为1的试件),对比如表7所示。

表7 计算值f与试验值f′对比
5 结论
(1)在相同力的效应作用下,ARCB试件的承载力较RCB有明显的提高,不只是承载力的简单叠加,极限承载力的提升幅度均在24%以上。
(2)角钢布置形式和布置位置能够影响梁的抗弯性能。对核心区混凝土约束效应最强的ARCB-3试件,其极限承载力相较于ARCB-1试件提升了8.5%,而ARCB-1试件比RCB试件极限承载力提升25%。
(3)内置角钢空间骨架的型钢混凝土梁其延性较普通钢筋混凝土梁效果更好。在受拉区和受压区同时布置角钢时延性更好。
(4)增大混凝土强度、角钢强度和受力钢筋强度均对内置角钢空间骨架的型钢混凝土梁有一定积极影响;在一定范围内,试件的极限承载力会随着剪跨比的增大而减小。
