全装配RC楼盖结构振动台试验与平面内刚度分析*
2023-08-03路晓军
庞 瑞, 徐 科, 徐 铸, 路晓军
(1 河南工业大学土木工程学院,郑州 450001;2 国网河南省电力公司经济技术研究院,郑州 450000)
0 引言
楼(屋)盖是建筑结构的重要组成部分,不仅承担楼层的恒、活载,还将水平地震作用和风荷载传递给各抗侧力构件。装配式楼盖结构主要有干式楼盖体系和湿式楼盖体系两种形式[1]。当前,我国应用较多的湿式楼盖是叠合式楼盖[2]。叠合式楼盖存在板缝易开裂且开裂后性能迅速降低的缺陷。当前,应用较多的干式楼盖是双T板楼盖体系,该体系可以满足大跨、重载等现代楼盖的设计要求,但存在板底面不平整、结构高度较大等问题,应用范围存在一定的局限性[3]。
基于此,庞瑞等[4]提出了分布式连接全装配RC楼盖(discretely connected precast RC diaphragm,DCPCD),以预制企口平板、夹层板或开孔板为基本构件,在挑耳梁上进行吊装平铺,通过分布式连接件连接的干式楼盖体系,其构造示意图见图1。

图1 全装配楼盖示意图
楼盖的平面内刚度及其隔板性能直接影响结构的动力特性和地震响应[5]。全装配楼盖平面内刚度有限,水平地震下,楼盖将发生明显的平面内变形,使得结构的地震作用计算、结构地震响应等与现浇结构有显著差异[6]。
Schoettler等[7]对一个采用装配式楼盖的三层单跨三开间预应力装配整体式框架-剪力墙结构进行了1/2缩尺模型振动台试验,试验模型的一层采用PC多孔板加叠合层的楼盖,二层采用PC双T板加叠合层的楼盖,三层采用干式连接双T板楼盖。结果表明,尽管制作与安装误差导致试验中后期出现预料之外的破坏,但不影响结构的整体性能;连接件的性能达到了预期效果;楼盖的破坏区域与基于能力设计方法预测的区域吻合;因楼盖平面长宽比较大,楼盖的平面内变形明显。吕西林等[8]对一个1/5比例的三层两跨两开间预制钢筋混凝土框架结构完成了振动台试验,楼盖为预制槽形板,结果表明结构的节点刚度退化迅速,层间位移较现浇结构明显偏大,但梁、板、柱等构件均较为完好。
由上述分析可知,国内外在装配式楼盖建筑振动台试验方面已经开展了较多研究,但在采用全装配楼盖的PC结构方面的振动台研究相对较少。为研究采用全装配式楼盖的建筑结构的动力特性和地震响应规律,提出该类结构的抗震设计方法,设计并制作一个四层单跨两开间的PC框架-剪力墙结构,拟对采用DCPCD的框架-剪力墙结构进行振动台试验研究,分析采用全装配式楼盖的建筑结构的动力行为、考察楼盖在地震作用下的隔板性能等。
本文介绍了采用DCPCD结构振动台试验模型的设计与制作,同时对试验模型进行了数值模拟分析与试验结果对比,以期为该类结构的研究和应用提供参考。
1 试验设计
1.1 试验概况
振动台试验原型结构为层高3m的四层单跨两开间采用DCPCD的框架-剪力墙结构。结构在X向两跨,轴线距均为3m;在Y向一跨,轴间距为5m。抗震设防烈度为7度(0.15g),地震分组为第二组,框架等级为二级、剪力墙抗震等级为三级,地面粗糙度为B类。试验模型长度比系数lr为0.25,试验模型的平面布置图、模型示意图和实景照片见图2。
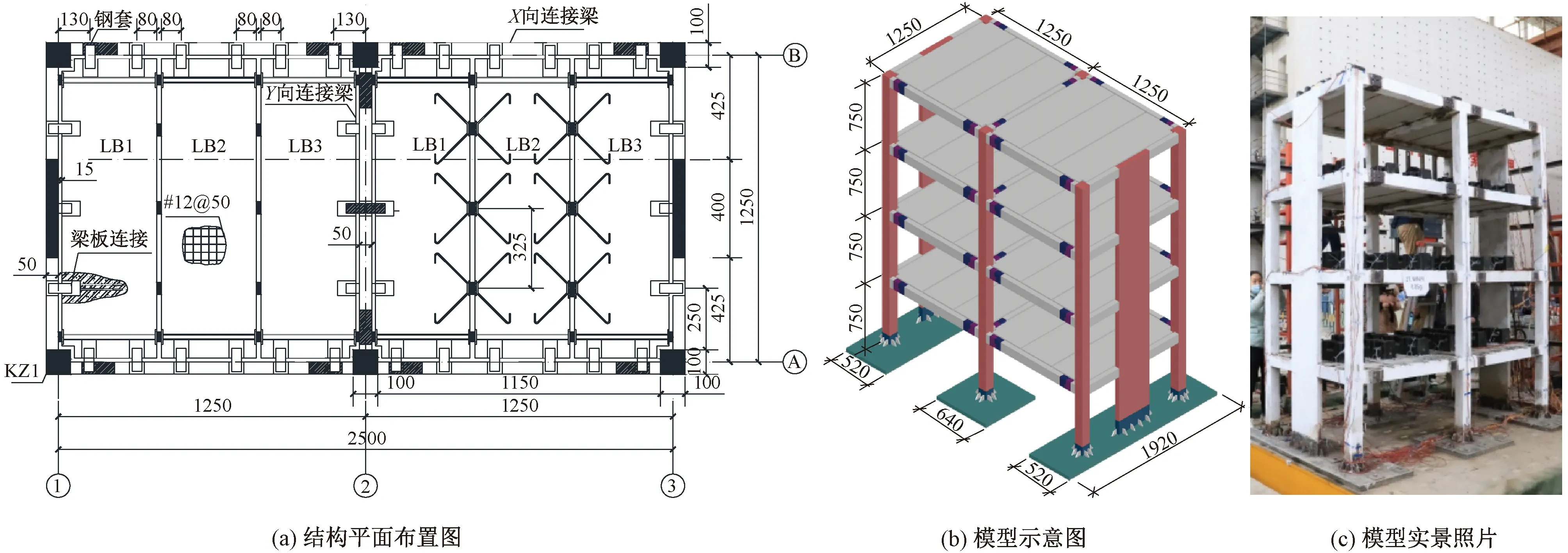
图2 试验模型参数图及实景照片
1.2 振动台
试验采用的三维六自由度地震模拟振动台试验系统,振动台系统的台面尺寸为3m×3m,最大负载为10t,最大加速度为±2g,最大速度为±0.7m/s,最大位移为±150mm,试验频率为0.1~50Hz。
2 模型设计
2.1 模型配重设计
因振动台的竖向承载能力有限,其人工质量的设置难以实现,而采用忽略重力的模型,试验结果的适用性又受到很大限制。因此,在不超过振动台竖向承载能力的条件下,应尽可能多地设置人工质量[9]。模型进行了以下验算,以确定采用哪种相似关系。现已知原型自重mp=174800kg,活载和非结构构件质量m0p=20000kg,试验所用地梁质量md=900kg。根据长度相似比和模型构件材料密度计算得出的模型结构构件质量mm为:
mm=mplr3ρr
(1)
式中:lr为长度相似比;ρr为材料密度相似比,当使用人工质量模型及原型材料时,ρr=1。
mm通过实际制作中材料用量修正得4500kg。模型中设置的人工质量ma为:
ma=Erlr2mp-mm
(2)
式中Er为弹性模量相似比。
模型中活载和非结构构件的模拟质量m0m为:
m0m=Erlr2m0p
(3)
式中M0p为原型中活载和非结构构件的质量。
(1)人工质量模型
由式(2)、(3)得,ma=5332.5kg,m0m=1125kg。人工质量模型相似律公式中的加速度ar=1,重力加速度gr=1,时间tr=0.5,频率ωr=2。模型自身质量与人工质量、活载质量之和为10.9t,超出了振动台的极限承载能力10t,故人工质量模型不能实现。
(2)忽略质量模型
忽略重力模型中的活载和非结构构件的模拟质量为:
m0m=ρrlr2m0p
(4)
由式(4)得,m0m=1250kg。忽略重力模型相似律公式中的加速度ar=1.9,时间tr=0.3,频率ωr=3.3。虽然模型自身质量与活载质量之和为5.75t,不超过振动台承载能力,但重力效应仅为实际应有重力效应的52.4%。将使试验结果产生重大误差,故不宜采用。
(3)欠人工质量模型
由式(3)得,m0m=1125kg。根据振动台最大承载力,取ma=1920kg,此时等效密度为2.47,相似律公式中的加速度ar=1.45,时间tr=0.41,频率ωr=2.41。欠人工质量模型的质量为7.6t,因设置了部分人工质量,模型的重力效应达到应有重力效应的63%。
虽然,欠人工质量模型的质量(模型结构自身质量与人工质量之和)没达到人工质量模型总质量的75%[9]。但是,由于模型底盘设置合理,能避免因人工质量不足而出现的模型底部先于实际结构破坏及上部结构的破坏减缓,可减小试验误差。因此,该欠人工质量模型的设计是可行的。
2.2 相似关系系数的确定
相似理论依据Bockingham Π定理,相似设计中采用的方法为一致相似律。式(5)为相似比设计中的基本方程,根据试验模型体量及试验材料确定长度相似比为0.25,弹性模量相似比为0.9;根据振动台承载能力设置人工质量,确定质量密度相似比为2.48。通过3个基本相似比,可计算得到其他物理量的相似关系,见表1。
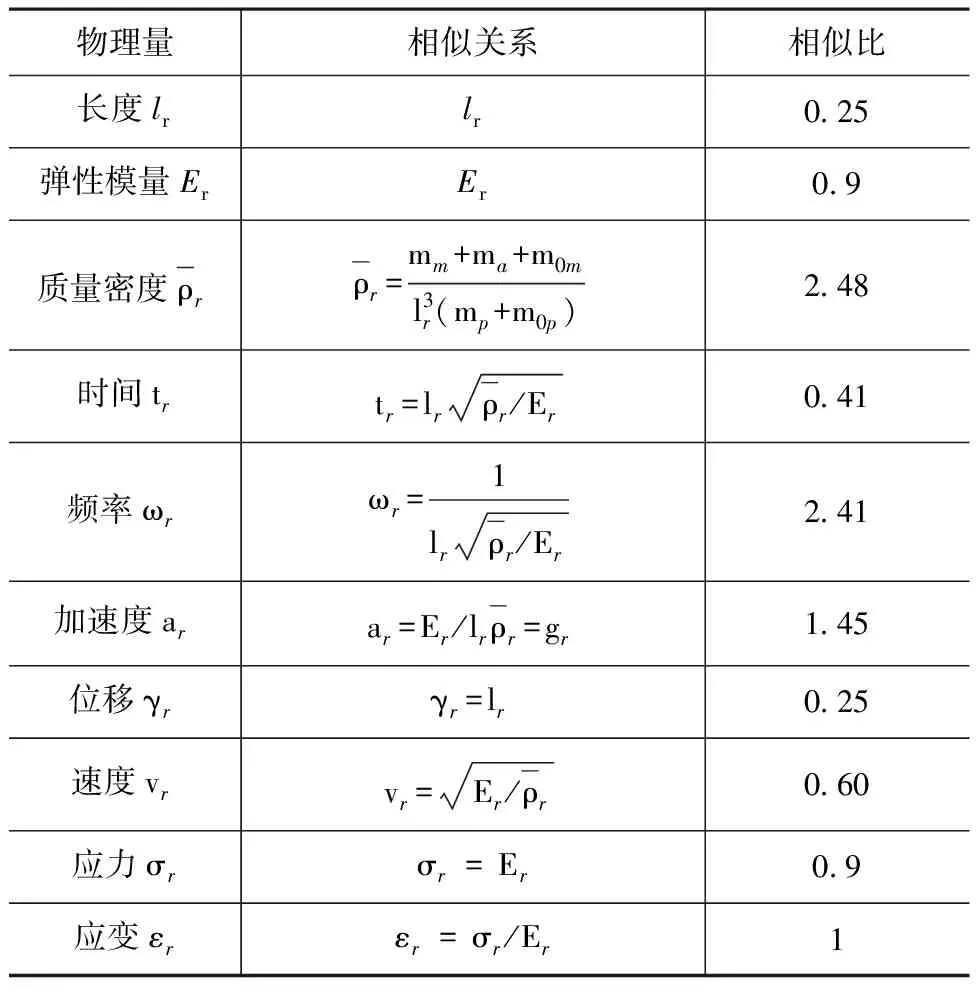
表1 模型主要相似系数
式中:SE为弹性模量相似比;Sρ为密度相似比;Sa为加速度相似比;Sl为长度相似比。
2.3 模型配筋相似设计
为保证DCPCD平面外承载力与原型结构相似,进行了模型配筋相似设计。设计钢筋混凝土结构试验模型时,可依据抗弯能力等效的原则控制正截面的承载能力,依据抗剪能力等效的原则模拟斜截面承载能力[10-11]。根据文献[12]相似配筋设计可知:
式中:As为纵向钢筋截面面积;S为相似常数;其余参数含义详见文献[12]。
通过有限元程序计算得出原型结构的配筋,再通过等强度配筋关系,可得缩尺模型的配筋,如表2所示。

表2 模型结构配筋
2.4 楼盖设计
Zheng等[13]研究表明,水平荷载作用下双T板通常被视为水平放置的深梁,可采用等效梁模型理论分析其平面内受力与变形。本文所研究的DCPCD与双T板楼盖同属于干式连接楼盖,主要通过楼板之间的连接件传递楼盖的内力,亦可采用等效梁理论进行楼盖平面内变形分析[5]。
为保证DCPCD平面内刚度与原型结构相似,试验中楼盖顺板缝方向根据相似关系系数,强度相似关系及等效梁理论进行了平面内刚度的相似设计,楼盖顺板缝的平面内刚度可表示为:
式中:K为楼盖顺板缝的平面内刚度;ξb为边榀框架位移;ξa为中榀框架位移;h为楼板跨度;Kr为楼盖顺板缝的平面内刚度相似比;ξbm为模型结构边榀框架位移;ξam为模型结构中榀框架位移;ξbp为原型结构边榀框架位移;ξap为原型结构中榀框架位移;hm为模型结构楼板跨度;hp为原型结构楼板跨度。
由表1可知εr=1,因此,可得:
均布荷载作用下,楼盖跨中弯曲变形ωm1和剪切变形ωm2分别为[5]:
式中:q为均布荷载;l为楼盖长度;Mi为作用在第i条板缝处的弯矩;Vi为作用在第i条板缝处的剪力;Ωθ为预制板板缝弯曲刚度;ψs为板缝处抗剪刚度总值;G′为等效梁模型剪切模量;A′为等效梁截面面积;E′为等效梁弹性模量;I′为等效梁截面惯性矩。
ψs=∑kvi
(13)
Ωθ=∑kpihpi2+∑ksjhsj2
(14)
式中:kpi为第i个受压连接件抗压刚度;ksj为第j个受拉连接件抗拉刚度;hpi为第i个受压连接件到中性轴的距离,mm;hsj为第j个受拉连接件到中性轴的距离,mm;kvi为第i个连接件的抗剪刚度,kN/mm。
联立式(9)~(12)、(15),可知模型中ψs与Ωθ满足:
(16)
式中:下标p表示原型结构;下标m表示模型结构。
在试验设计过程中,根据缩尺后的平面尺寸预确定连接件的尺寸及个数,从而确定ψsm,最后通过式(16),确定Ωθm及连接件的尺寸。
2.5 试验工况
为使输入地震波的特性与建筑场地类别和设计地震分组相符合,并且与结构振动特性相关,选用El Centro波(EL)、汶川波(WW)、人工波(ZW),加载方向为顺板缝方向(Y向)。所采用的3条地震波的反应谱对比见图3,加速度时程及振幅频谱见图4。试验采用分段加载的加载制度,每段加载由3条地震波组成,加载完成后进行双向白噪声扫频(WNX、WNY),具体加载方式及工况见表3。
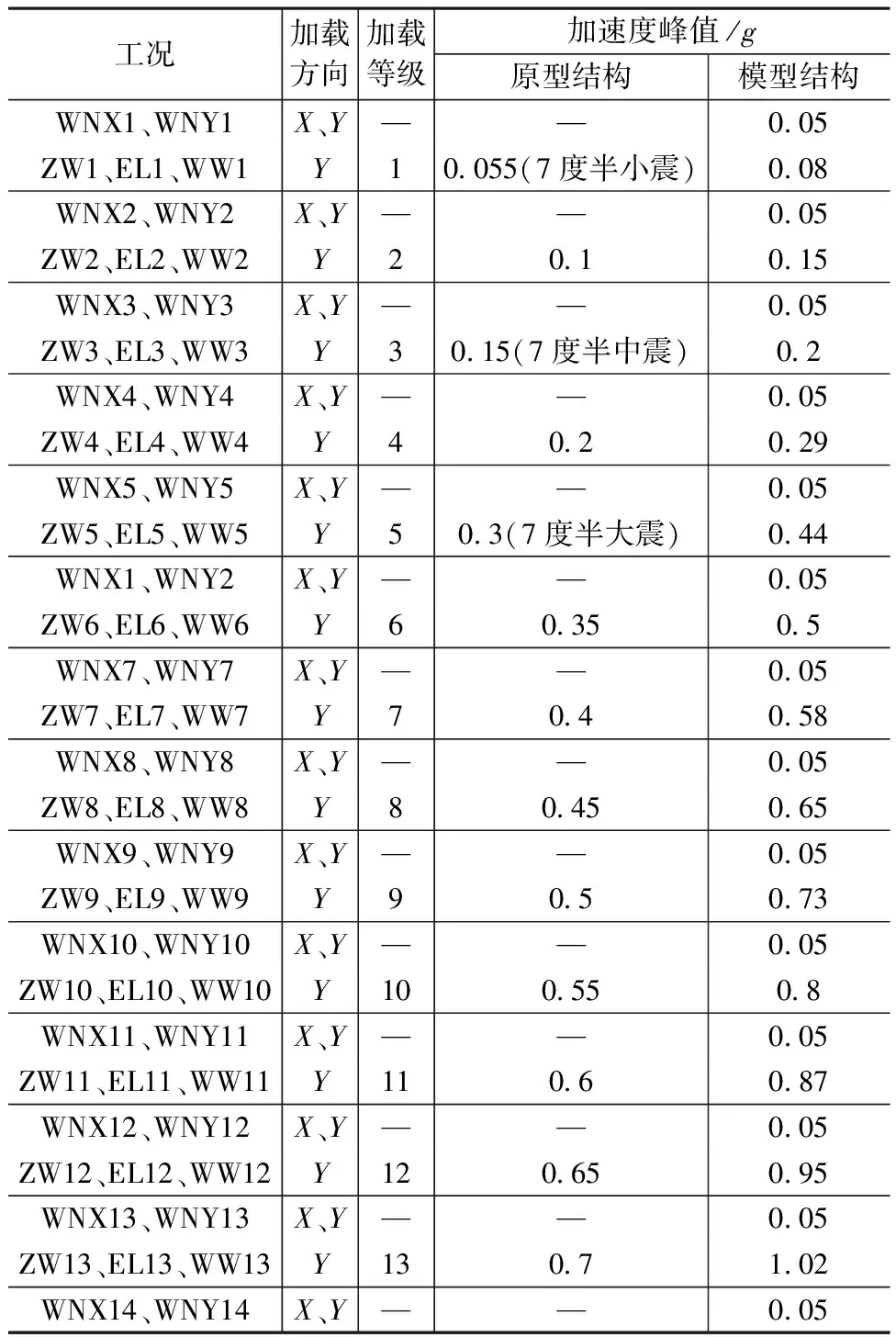
表3 加载制度

图3 反应谱对比图
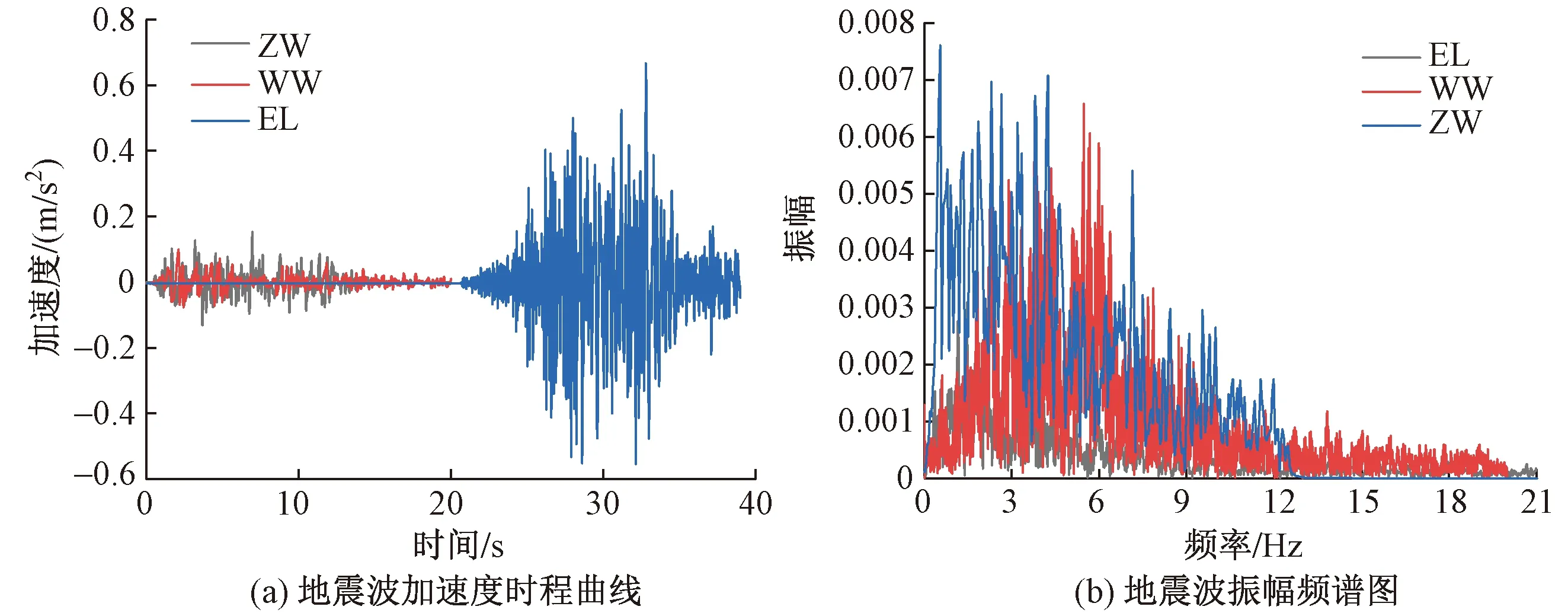
图4 地震波加速度时程及振幅频谱图
3 数值模拟结果及试验数据分析
3.1 弹簧单元数值分析方法
在全装配式楼盖平面内受力特性分析方面,Zheng等[14]提出了基于等效梁模型的全装配式楼盖平面内刚度计算方法(简称等效梁方法),文献[5]采用该方法进行了DCPCD动力特性与地震响应研究。该方法假定连接件的拉压刚度相等,未考虑PC板实际内力效应,使得计算精度不够。
同样基于等效梁模型理论,为了更好地模拟DCPCD结构的地震响应,本文提出了考虑连接件拉压刚度不等[15]、PC板实际内力效应的全装配式楼盖平面内刚度数值分析方法(简称连接件方法)。
全装配式楼盖的数值分析中,板缝连接节点的模拟是保证分析准确性的关键。在DCPCD建筑结构模拟中,释放板与梁的约束,板-板及板-梁之间均采用弹簧单元连接[16-17]。板-板连接和梁板连接的力学模型如图5所示。

图5 板-板连接和梁板连接的力学模型
采用上述数值分析方法,拉压弹簧、剪切弹簧刚度取文献[3]试验实测值。建立文献[17]中的有限元分析模型,采用单调加载模式,数值模拟、理论计算值与试验值的荷载-位移曲线对比如图6(a)所示。由图可知:在加载初期,楼盖处于弹性,数值分析结果与试验值吻合良好,能够较好地模拟楼盖在弹性阶段的受力特性。

图6 数值分析结果与试验结果对比图
提取了DCPCD试件在弹性阶段(文献[17]中提到的DCPCD试件弹性阶段最大荷载为108kN)沿楼盖长度方向的挠度试验值和有限元计算值进行分析,见图6(b)。由图可知,在弹性阶段,数值模拟各点位移与试验值吻合良好,弹簧单元模型可以较好的分析DCPCD楼盖在拟静力作用下的平面内受力特性。
3.2 数值分析结果对比
为对比数值分析方法在动力作用下的分析效果,建立了振动台试验原型结构的弹簧单元分析模型、等效梁模型和现浇对比模型,并进行了结构动力特性与地震响应分析。三种模型模拟各类结果对比如表4所示。
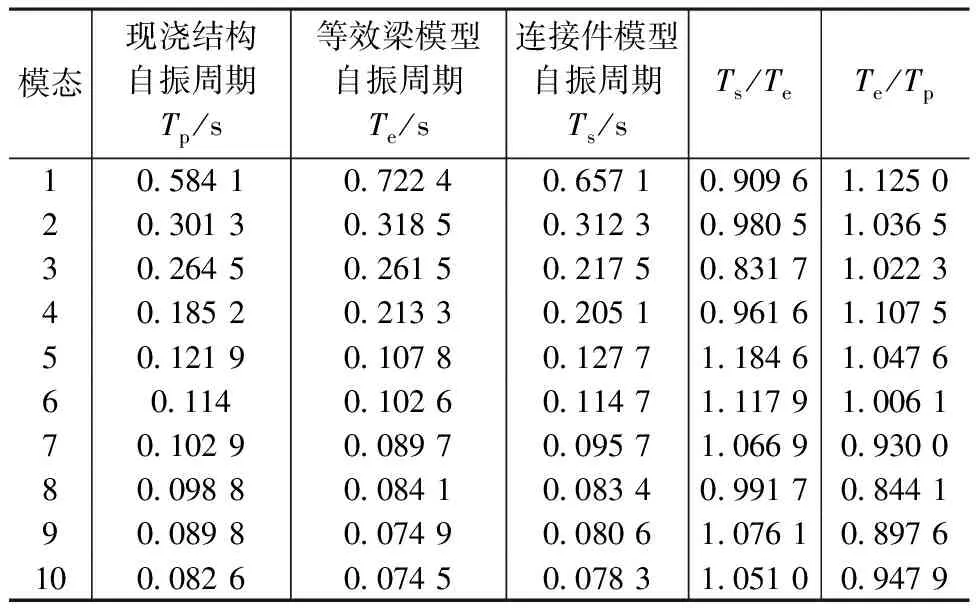
表4 自振周期结果对比
由表4可知:前10阶振型中,弹簧模型自振周期与等效梁模型的比值在0.8317~1.1179,说明两种分析模型分析结果接近,能较好地应用于DCPCD结构的抗震分析;在前6阶模态中,DCPCD结构的自振周期是现浇结构的1.0061~1.1250倍,说明DCPCD的存在降低了结构刚度。3种分析模型在7度半多遇EL波作用下的地震响应如图7所示。

图7 地震响应模拟结果
由图7(a)可知,弹簧模型与等效梁模型两种模型的加速度随着楼层高度的增加而增加,趋势基本一致;DCPCD结构的地震响应在底部两层与现浇结构相差不多,在顶部两层相差较大。由图7(b)可知,水平地震作用下,两种DCPCD结构分析模型均发生了明显的平面内变形,而现浇结构的平面内变形基本为0;DCPCD结构中楼盖相对挠度(楼盖的最大平面内变形与楼盖长度之比)由下到上逐渐变大,顶层楼盖的相对挠度为1.25×10-4,不满足我国规范对刚性楼盖相对挠度不大于1/12 000的要求,也不满足国外文献对刚性楼盖相对挠度不大于1/50 000的要求[5,18]。证明在采用新型楼盖的建筑结构抗震分析与设计时,不能采用刚性楼盖假定。
综上所述,在水平地震作用下,DCPCD结构与现浇结构的差异主要表现在:DCPCD结构的整体刚度小于现浇结构,表现为DCPCD结构基本周期大于后者;与现浇结构相比,DCPCD结构的楼层加速度响应大于后者;水平地震下,DCPCD结构的楼盖发生了较大的平面内变形,而现浇结构楼盖的平面内变形较小,可以忽略。
3.3 试验结果分析
7度半多遇地震作用下,各层梁柱节点侧向位移如图8所示。由图8可知,在三种地震波作用下,楼盖均发生了显著的侧向位移,且随着楼层增大,侧向位移呈增大趋势。

图8 7度半多遇地震作用下各层梁柱节点侧向位移
模型结构在7度半多遇地震下相对挠度如图9所示。由图9可知,在7度半多遇地震作用下结构相对挠度在1层小于1/50 000,满足国内外规范对刚性楼盖的要求,在2、3、4层小于1/12 000,但大于1/50 000,只满足国内规范对刚性楼盖的要求,不满足国外规范要求。
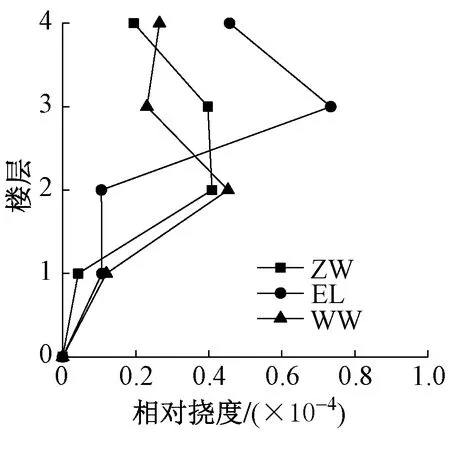
图9 模型结构在7度半多遇地震作用下相对挠度
试验结果与模拟结果对比表明,等效梁模型与提出的基于连接件实测力学性能的弹簧单元模型可以准确地模拟DCPCD结构在水平地震作用下的响应。
4 结论
(1)采用欠人工质量模型,模型的重力效应达到应有重力效应的63%以上,减小了重力失真效应对试验结果的不利影响。
(2)等效梁模型与连接件模型两种分析方法能较好地模拟DCPCD结构的地震响应。
(3)水平地震作用下DCPCD发生了较大的平面内变形,使得结构的地震响应与现浇结构存在较大差异;DCPCD不满足刚性楼盖假定,抗震设计时建议考虑楼盖平面内变形对地震作用和地震内力分配的影响。
