多尺度分析方法在土力学教学中的应用探讨

周凤玺 侯彦东 王立宪

摘  要：土力学作为一门土木工程相关专业十分重要的专业基础课程，其课程内容具有学科综合性强和地域实践性强的显著特点。与逻辑严密的连续固体力学相比较，土体的多孔多相性和散粒性使得土力学课程的概念繁多，内容连续性相对较差。为进一步提高土力学课程的教学质量，从理论教学和实验教学改革的角度对多尺度分析的教学方法进行应用探讨。通过对土体微细观特性到宏观现象的耦合关联，从不同尺度层次分析土的物理力学特性，以期使学生能够从不同维度去理解土力学各个知识点之间的内在联系。

关键词：土力学；专业基础课；理论教学；实验教学；多尺度分析

中图分类号：TU50    文献标识码：A    文章编号：1673-7164（2023）13-0026-04

土力学是利用力学的一般原理，研究土的物理、化学和力学性质及土体在荷载、水、温度等外界因素作用下工程性状的应用学科，它是力学的一个分支，是以土为研究对象的学科。土力学课程是土木工程相关专业十分重要的专业类基础课课程，融合了材料力学、弹性力学、流体力学、工程地质学以及土工测试技术来研究土的物理力学性质和工程特性，是一门综合性和实践性很强的学科。土是具有颗粒离散性和三相物质组成的，土体在宏观上具有整体连续性。因此，土力学具有理论繁多、内容连续性相对较差、应用公式多、推导公式假设多的特点。土体的各种物理力学性质与微观结构组成密切相关，在教学中要让学生从逻辑严密的固体力学思维方式转变到微细观特性到宏观现象的相互了联系，形成多尺度分析的土力学思维方式［1-2］。

文章探讨多尺度分析方法在土力学教学中的应用，优化课堂教学内容，加强教学内容各章各知识点的内在联系，使其更加具有层次性和条理性。

一、多尺度分析方法

多尺度科学的本质在于研究不同尺度层次，包括空间、时间或者其他物理量尺度相互耦合的系统科学。多尺度科学的研究历史悠久，其研究领域涵盖了几乎所有的自然科学和工程科学，对于诸如材料科学与工程、环境科学与工程、土木工程等工程学科研究而言，多尺度分析是它们的一个共同核心［3］。因此，多尺度分析方法对于当代科学与技术复杂问题的解决有着显著的优势。

土体力学行为的多尺度现象在于微观、细观和宏观不同尺度层次上的相互关联和样性和耦合作用［4］，集中表现为土体不同颗粒组成、排列组合以及孔隙结构等对其宏观强度、变形和稳定性等特性的影响［5-6］。与科学研究方面的应用相比较，多尺度分析方法在教学活动中鲜有探索和实践。

二、土力学课程中的多尺度分析

土体作为自然界的产物，在形成过程中风化、搬运和沉积等环节交错反复作用，同时伴随复杂多样的自然气候等环境，因此，土的成因类别及其物理力学性质具有显著的差别。土的性质一方面取决于原始沉积条件所决定的土粒矿物成分、粒间微观结构以及粒间孔隙中流体特性等，另一方面也与沉积以后的变化历程，如水文地质条件的变迁、应力状态的改变沉等密切相关。

目前，在土力学教学中，通常土体被简化为均匀同质性材料，以便于采用传统的弹塑性理论进行分析和求解。土体是一种松散的堆积物，而土体颗粒体自身的矿物成分、粒径大小、联结形式等对颗粒集合体物理力学性质影响非常关键，土体的渗流、强度和变形等工程性质都受到了微细观尺度层次的影响［5-6］。然而这些因素和影响规律在土力学的教学过程中往往没有得到很好的体现。土体可根据不同的尺度分为微观、细观和宏观三个层次（如图1所示），比如工程中所涉及的土体一般考虑其宏观性质，而尺度效应试验中涉及土体则为细观，研究土体颗粒间的各种微观作用力一般为微观［5-6］。

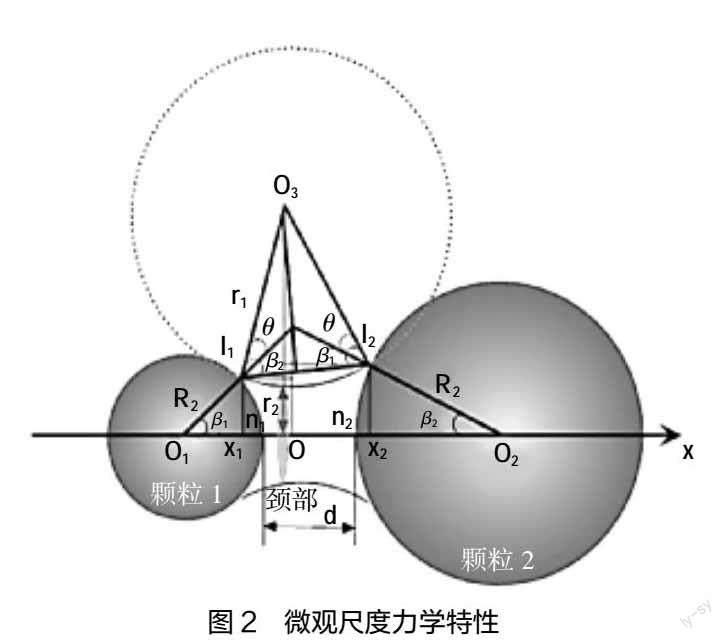
土体力学的微观特征（如孔隙、颗粒、粒间力等）主要体现为范德华力、库仑力、液桥力和毛细压力等之间的相互作用（如图2所示）。土体的微观结构对土的力学性质有着很大的影响。

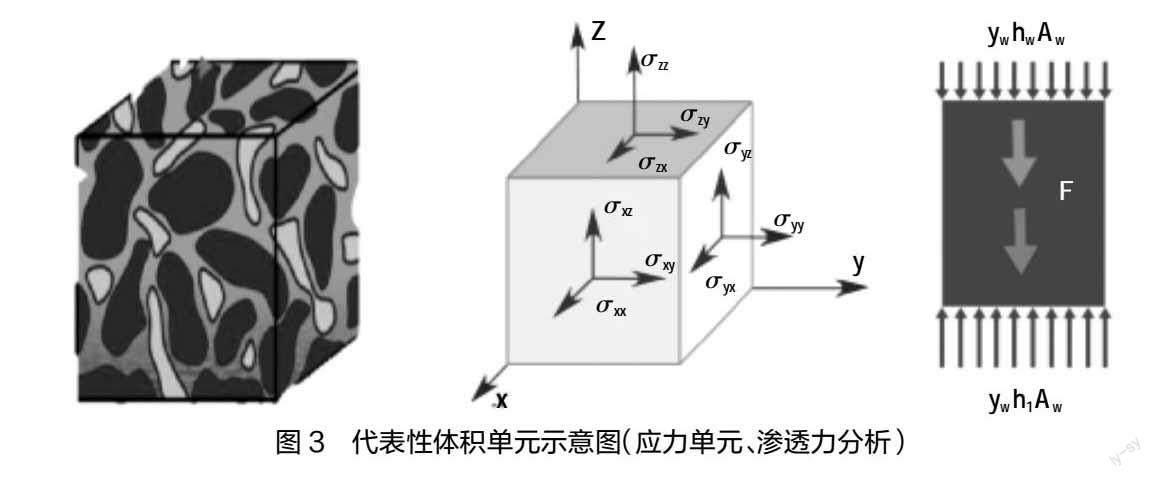
土体的细观尺度是土体中土颗粒骨架组构的排列组合等相互关系，其尺度大于微观结构而远小于土体的宏观构造，其应具有相对稳定的轮廓边界以及一定程度上反映力学行为的单元［5］。这里提到的细观层次是指土体的代表性体积单元如图3所示，传统的室内土工試验项目几乎都是针对这一尺度进行的［7］。细观层次是联系土体宏观响应和微观组成的桥梁纽带，是建立土体多尺度耦合作用的重要环节。

宏观尺度主要是考虑工程特性并侧重于应用方面的分析，如土与结构的相互作用、地基沉降、边坡稳定性问题等（如图4所示）。

土力学课程内容涉及的前修课程多，各章节之间没有固体力学课程的逻辑性强，学生感觉土力学课程内容条理性差、重点散乱且系统性不强。如何使学生理清相关内容之间的联系，是课程教学的一个重点工作和决定教学质量的关键因素。

在教学过程中，教师应建立完整的多尺度授课内容，将看似相互独立的内容从微细宏观多尺度结构层次上进行讲解，从作用机制和力学响应方面将各章节的内容关联起来，培养学生从不同尺度分析问题的能力，以期在以后的学习工作中能有效应用多尺度分析方法综合并有效解决工程实践中遇到的技术问题。

三、多尺度分析在教学实践中的应用

（一）多尺度分析在理论教学中的应用探讨

目前本学科所学的经典土力学理论基础仅建立在单一的宏观尺度之上，因此传统授课方式多从宏观的角度进行讲述而并未考虑土体本质上的颗粒性和结构性特征，忽略了微观层次和细观层次上的多样性和耦联机制，导致同学们在学习过程中只是想学习和掌握了一些浅显的基本概念，而不能真正地由表及里，探其究竟，很难激发学生的学习兴趣。

土体介质可看作是固体矿物颗粒、粒间孔隙溶液、孔隙气体和土颗粒间的胶凝物（如有机质和胶凝状氧化物等）等物质组成的多孔多相介质，在形成过程中具有多相性、碎散性、变异性等天然的物理性质和弹塑性、剪胀性以及固液相变等特殊的力学性质。土体中不同粒径的固体颗粒形成了土体的骨架，级配和粒间孔隙特征地形成了复杂的内部微观结构和细观组构，对土体的宏观力学行为和工程特性产生了显著的影响［5-6］。

因此，针对土体不同尺度层次的相互耦合效应对土体的力学特性展开讲解，能够深入剖析土力学课程中相关问题的重点和难点，帮助学生更好地进行学习。

以边坡稳定分析章节为例，从微观颗粒尺度、细观材料尺度和宏观场地尺度三种不同层次进行分析讲解［8］。

在课堂授课环节中可以首先从宏观角度介绍国内外典型的边坡工程失效案例，让学生对边坡的稳定性问题以形象直观的认识，从而引发学生对边坡工程问题的思考；接着，从微观尺度上介绍不同土体颗粒的形状、大小、级配、排列方式及其粒间主要作用力等因素对力学行为的影响规律，从而与前面章节讲授的土体基本物理特性、抗剪强度理论等内容相互联系起来；然后，利用现有的离散元模拟软件（如PFC等）针对简单土坡进行失稳过程演示，讲解颗粒间的粘结、颗粒表面摩擦系数等的影响程度，并展示剪切带的形成和演化过程，使学生对边坡的失稳过程和影响因素有了较全面的认识；最后，从宏观层次上分析边坡的稳定性，可以通过展示有限元等数值方法计算得到的同一边坡的响应过程，展示边坡中的应力云图、变形云图等，并与离散元的结果进行比较，再一次强调微观参数对宏观响应的影响机制（讲解过程如图5所示）。当然，限于课程学时的限制，在课堂上不可能进行建模、计算和分析等全过程操作，只能是教师在课前提前做好授课素材准备，提高教学效率。

讲解过程中通过数值分析软件的仿真演示，让学生从中思考土体的微细观状态变化与其宏观响应之间的联系，充分了解细观尺度上的不同如何影响宏观层次上的稳定性。

通过这一过程也能激发学生对土体力学性质和工程特性的学习兴趣和创新思维，有利于培养学生良好的学习习惯和独立思考能力。

（二）多尺度分析方法在实验教学环节中的应用

目前，土力学室内实验大多按照实验指导书进行，并且一般情况下只能做到了解基本的土工实验过程、操作方法和结果整理，而无法深入了解实验现象后面的本质机理，导致学生的积极性不高。

运用多尺度分析方法，在原有的实验基础上扩展，通过虚拟仿真将多尺度分析方法融入土工实验教学环节中，可以有效地帮助学生培养不同尺度思考问题的能力和对现象的科学分析能力。

以土体的直接剪切实验为例，在进行室内实验操作之前，同样先从典型的工程案例展示开始，让学生充分认识土体抗剪强度这一工程特性的重要性；然后从颗粒的相对运动，粒间孔隙分布变化来分析土体剪切带的形成和发展过程，并结合颗粒系统中传力过程的力链网络演化过程描述土体微观结构的变化对宏观力学行为的影响。通过从变形、传力等不同角度对剪切破坏过程的局部过程进行微观分析，以揭示试样在直接剪切过程中的破坏机理。

在实验过程中观察土体的状态变化、分析和理解其作用机理，能有效培养学生的提出问题、分析问题和解决问题的综合能力。

四、结语

文章针对传统土力学课程教学过程中存在的不足，从教学改革方面进行了探索和研究，结合多尺度分析在岩土工程中的研究成果，将多尺度分析方法引入教学环节中，并从理论教学和室内实验教学两个方面，对该教学方法的应用进行了阐述。旨在加强学生的土力学知识掌握程度，使其从本质上了解土体的物理力学特性，培养学习的主动性和独立思考、科学合理解决问题的能力，从而进一步有效提地高课程的教学质量。

参考文献：

［1］ 谢定义. 对高校土力学教学的回顾与展望［J］. 东南大学学报（哲学社会科学版. 高等教育研究），2008（03）：39-43.

［2］ 蒋金洋，刘志勇，佘伟. 多尺度分析方法在土木工程材料教学中的探索与实践［J］. 高等建筑教育，2017，26（02）：44-46.

Jiang J Y，Liu Z Y，She W. Exploration and practice of multi-scale analysis of civil engineering materials teaching［J］. Journal of Architectural Education in Institutions of Higher Learning，2017，26（02）：44-46.

［3］ 龍期威. 断裂分形研究的新热点——关于断口分维是否具有普适性的一场争论［J］. 物理，1997，26（01）：6-8.

Long Q W. New Hot spots in research on fracture fractal-a debate on whether the fractal dimension of the fracture is universal［J］. Physics，1997，26（01）：6-8.

［4］ 何国威，夏蒙棼，柯孚久，等. 多尺度耦合现象：挑战和机遇［J］. 自然科学进展，2004，14（02）：121-124.

［5］ 冯德銮. 土体介质多尺度耦合力学特性的理论与试验研究［D］. 广州：华南理工大学，2016.

［6］ 彭旭铮. 土体多尺度变形理论及计算分析［D］. 广州：华南理工大学，2015.

［7］ 陈云敏，陈仁朋，詹良通，等. 岩土工程的多尺度试验［A］//土工测试新技术——第25届全国土工测试学术研讨会论文集［C］. 杭州：第25届全国土工测试学术研讨会，2008.

［8］ 涂福彬. 岩土体灾变过程多尺度数值分析方法研究［D］. 杭州：浙江大学，2014.

（责任编辑：淳洁）