新安江模型与水箱模型在马家沟水库洪水预报的适用性研究

马靖航,咸永财,何学平,刘 明,韩牧原,杜佰林,阮炳南,许鎏佳,吴 磊*

(1.国能陕西水电有限公司,陕西 西安 710000;2.西北农林科技大学旱区农业水土工程教育部重点试验室,陕西 杨凌 712100;3.西北农林科技大学水利与建筑工程学院,陕西 杨凌 712100)

洪水预报是直接为国民经济建设服务的重要基础性工作[1-3]。它是根据洪水形成和运动规律,利用水文、气象信息,预测洪水的发生与变化过程的应用基础性技术科学[4]。准确的洪水预报是防汛抢险和防洪系统调度运用的决策依据[5-6]。同时,也为减少洪灾损失争取时间、有助于更好地控制和利用洪水资源,是重要的防洪减灾非工程措施,对于优化水库调度、确保防洪安全具有重要意义[7-8]。

通常,把预见期在2 d以内的洪水预报称短期预报,洪峰水位、洪峰流量、洪现时间和一次洪水总量等是主要的预报项目。短期洪水预报多采用基于物理成因、有一定理论基础的经验性方法。这类方法的优点是结构简单、使用方便,但缺乏物理意义,模拟精度不高[9]。随着计算机水平的快速发展,流域水文模型已逐渐成为现代实时洪水预报系统的核心模块[10-12]。国内外相继提出了Sacramento、TANK、新安江、HBV、TUWMODEL、HEC-HMS、TOPMODEL、SHE、VIC、流溪河模型等一系列集总式和分布式水文模型,以及多种模型参数优化方法,洪水预报也随之发展[13-17]。

概念性水文模型相比黑箱模型以及分布式水文模型,由于其数据需求量相对较小而常用于历史资料欠缺的地区[18]。新安江模型与水箱模型是概念性水文模型的典型代表,它们以物理成因为基础,采用概化和假设的方法对水文现象进行数学模拟,模型的结构和参数具有一定物理意义。新安江模型由河海大学赵人俊教授团队提出,模型最初为二水源新安江模型(地表径流和地下径流),后引入萨克拉门托模型与水箱模型中线性水库函数划分水源的概念,提出了三水源新安江模型(地表径流、壤中流、地下径流),在中国湿润和半湿润地区应用广泛,取得了较好的效果,其主要特点是蓄满产流结构[19-20]。水箱模型(Tank model)是1961年由日本的菅原正已博士构建,经后续研究者的不断改进和更新换代逐渐成为一种被广泛应用的水文模型[21]。水箱模型能以水箱中蓄水量出流关系来模拟复杂的降雨径流转换过程,结构灵活、适用性强,在洪水预报、水沙研究等方面应用良好[22-23]。

湑水河干流自上而下分观音峡水电站、金龙水电站、黑峡子水电站、八仙园一级水电站、八仙园二级水电站、马家沟水电站等共 11 级开发。观音峡水电站为第一级,控制流域面积431 km2,装机容量2.6万 kW,为引水式水电站,年均入库径流量19 731 万m3。马家沟水电站位于湑水河中游,为第六级,坝址位于石槽河汇合口上游约3.0 km处,控制流域面积1 311 km2,具有防洪、发电等功能。电站厂房位于石槽河汇合口上游处,流域面积1 323 km2,属坝-引水混合式水电站。

本文以马家沟水库为对象,分别选用新安江模型和水箱模型模拟马家沟水库流域近3 a的日径流过程与次洪过程,采用遗传算法(GA)率定模型参数,从模拟效果、指标误差等方面对比分析新安江和TANK模型在水文模拟过程中的适应性,综合评估2种洪水预报方法的可靠性。研究结果对及时发出洪水灾害预警、制定防洪措施、减少洪灾损失具有重要意义。

1 研究方法

1.1 流域概况

马家沟水库位于陕西省城固县,地处汉江一级支流湑水河中游,多年平均径流量6.43亿m3,水库正常蓄水位794 m,正常蓄水位以下库容2 706万m3。流域属北亚热带湿润季风气候,雨量年际变化大,年内分配不均;地形以秦岭山地丘陵为主,地势高、起伏变化大、河谷纵横交错,河系支流呈羽型分布。流域全年温暖湿润,符合新安江模型、水箱模型的应用条件。

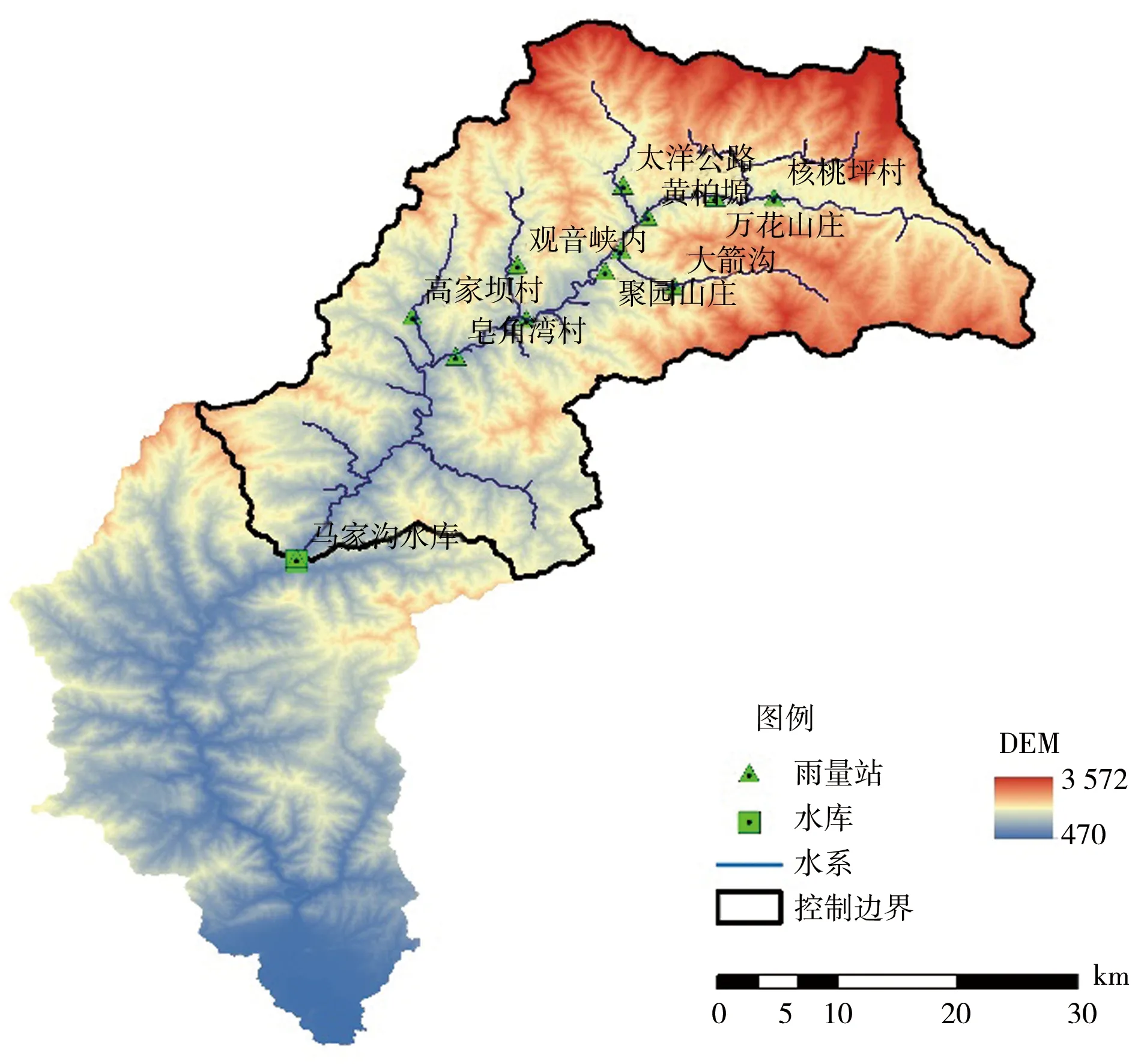
图1 马家沟水库流域水系及水库、雨量站位置分布

1.2 新安江模型与水箱模型

三水源新安江(XAJ)模型采用蓄满产流概念,对降雨空间分布不均匀采用分单元产流计算,流域调蓄对坡面不同水源的差异采用分水源汇流计算,坡面汇流与河网汇流的差异采用分阶段汇流计算,并引入了土壤蓄水量和自由水容量分布曲线[24-25]。模型整体包含蒸散发模块、产流模块、水源划分模块和汇流模块[26-28]。

水箱(TANK)模型是一种概念性径流模型,能以简单的形式模拟径流的形成,并将流域产汇流中各个水文过程,利用多个彼此联系的垂直串联水箱进行模拟[23]。除底层水箱没有底孔外,一般而言每个水箱都由底孔和边孔组成。其中边孔出流表示不同的径流产流,底孔出流代表土壤下渗,同时也是下层水箱的入流,因此一个简单水箱通常有3个主要参数,分别为边孔高度,水箱边孔出流系数和水箱底孔下渗系数[25]。

1.3 数据来源与处理

研究所使用的气象、流量数据均来源于国能城固马家沟水电有限公司。在考虑峰高量大、降雨径流关系显著原则的基础上,根据搜集的2019—2021年水库逐日流量、水位和泄洪资料,整理得到9场历史洪水数据,每年各3场。域内量级和强度较大的暴雨一般出现在7—9月,洪水由暴雨形成,出现时间与暴雨基本一致,受暴雨特性的影响,洪水多为单式洪峰,受秋淋连阴雨影响也易出现复式洪峰。采用泰森多边形方法[29],计算黄柏塬等12个雨量站的面平均雨量,见式(1):

(1)

式中P——面降水量;Pi——站点降水量;wi——站点面积权重。

经降水量、降水历时、降水强度、洪量、洪峰流量、洪水历时、径流深、径流系数等指标的聚类分析,发现9场洪水具有一定的代表性。基于此,设定2019—2020年为日模率定期, 2021年为日模检验期;选用2019—2020年的6场代表性洪水用于次洪率定, 2021年的3场洪水用于次洪检验。

1.4 遗传算法与实时校正

遗传算法是Holland等于1975年模拟生物进化规律提出的一种随机、高度并行、自适应的搜索方法。与传统优化算法不同,遗传算法可直接对结构对象进行操作并自适应地调整搜索方向,不需要明确的规则。本文以MATLAB R2018b为开发工具编写遗传算法程序,优选模型参数,设定种群规模为1 000,染色体编码长度为50,交叉概率为0.75,变异概率为0.05,最大迭代次数为1 000,经多次试算求解以实现模型参数的优化。

为减少洪水预报的误差来源,在场次洪水过程模拟中引入了具有3 h预报时段的一阶自回归(AR(1))实时校正方法[30]。根据误差相依的特性,首先计算观测数据与模拟数据的误差序列,然后建立自回归模型并依据最小二乘法进行参数估计,最后计算校正后的预报值,获取预报结果。

1.5 预报精度评价指标与评定依据

洪水预报精度评定包括洪峰流量(水位)、洪峰出现时间、洪量(径流量)和洪水过程等,依据GB/T 22482—2008《水文情报预报规范》[31],选用洪量预报许可误差FR,洪峰预报许可误差FP,峰现时间预报许可误差FT和Nash-Sutcliffe (NS)效率系数作为评价指标对模拟结果进行精度评定。

1990年春，见廉小花对儿子特别好，徐河开始向廉小花套近乎。廉小花觉得徐河肯干，心地也不坏，自己和小云天又天生有缘，于是廉小花不顾家人的反对，于1990年冬天，执意嫁给了徐河。

2 结果与分析

2.1 日径流过程模拟分析

2.1.1日模参数率定

采用遗传算法对新安江模型的16个参数进行多次反复调试率定。首先随机生成初始群体,计算群体中每个个体的适应度,依次进行选择、交叉、变异运算,当进化代数等于最大进化代数时,将最大适应度个体作为最优解输出并停止优化。采用试错法和遗传算法对水箱模型日模参数进行设计/率定,首先采用4个边孔的单水箱模型对流域日径流过程进行模拟,确定出水箱模型的10个参数初值范围,然后分别调整水箱中上孔系数和下孔出流系数,并进行自动参数调试率定。统计新安江模型和水箱模型日模参数的率定结果,见表1。

表1 新安江模型和水箱模型的日模优化参数

2.1.2日模结果分析

新安江模型和水箱模型率定期、验证期日模精度评定结果,见表2。

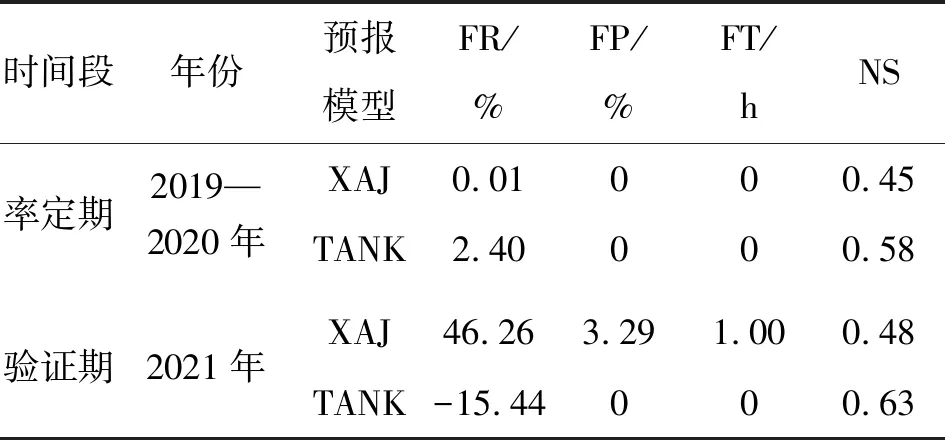
表2 新安江模型和水箱模型日值模拟精度评定结果

通过表2可以看出,新安江模型和水箱模型在马家沟水库流域均具有较好的适应性,对于旱期及汛期均具有较好的模拟效果,二者在率定期与验证期的各项洪水指标基本能满足洪水预报精度要求。为更直观地对比新安江模型与水箱模型在马家沟水库流域的适用性,分别将二者的日模拟结果与观测值进行对比,见图2。

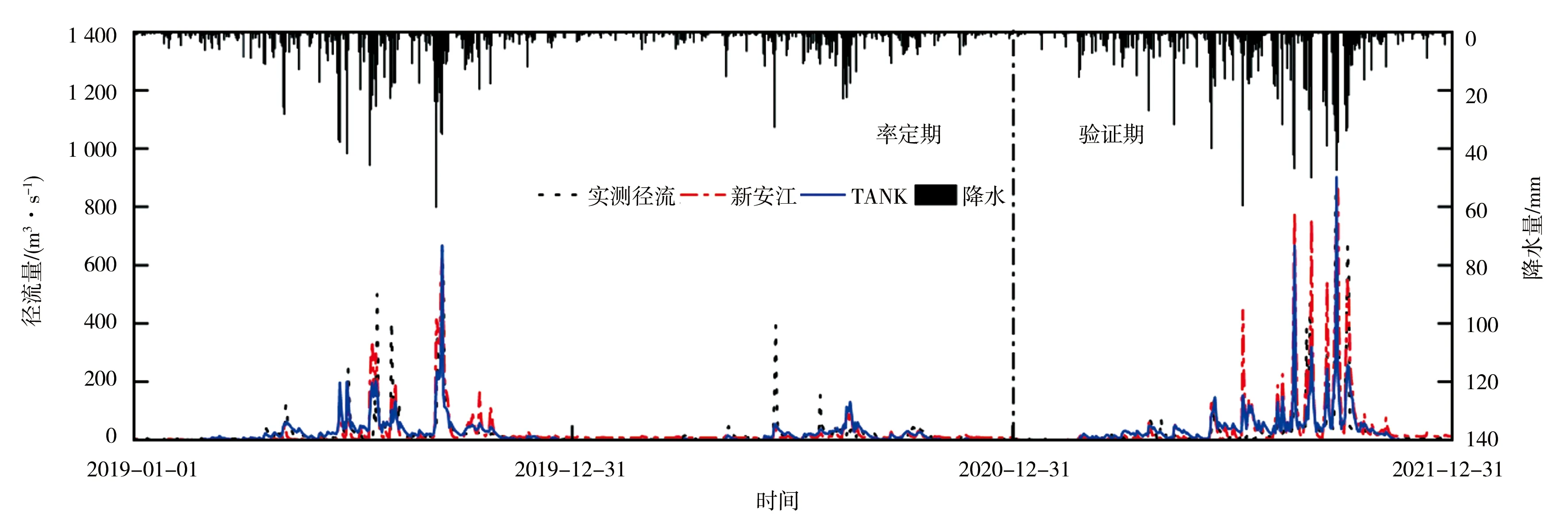
图2 2019—2021年马家沟水库日径流模拟结果对比

新安江模型在率定期对洪水模拟效果较好,仅在2020年出现模拟洪峰过低现象(图2),这可能是因为流域局部大暴雨而流域面降雨偏小导致与实测径流值偏差较大。在验证期新安江模型对模拟洪水存在高估现象,部分模拟洪峰在实际观测中峰量较低或不存在,分析可能是马家沟上游部分水库拦蓄洪水所致。水箱模型对于较大洪水能进行准确预报,其模拟偏差主要源于200 m3/s以下的小洪水,此类模拟误差可能是因为流域上游的观音峡等水电站串联调蓄对小型洪水产生了削峰作用。整体来看,2种模型在汛期的洪峰及洪量基本满足洪水预报精度要求,二者均可用于马家沟水库流域的水文过程预报。

2.2 次洪模拟过程比较

2.2.1次洪参数率定

新安江模型在次洪模拟的参数调试中,蒸散发参数K、WUM、WUM、WLM、C和产流参数IMP、B的取值参考了日值模型模拟的结果,水源划分参数SM、KG、KSS、EX和汇流参数KKG、KKSS、CS、CR、L则采用遗传算法率定优选得出。水箱模型在次洪模拟的参数调试中,采用了具有3、2、1个边孔的三水箱模型,考虑到洪水开始前均处于基流阶段,将模型初始蓄水量设置为0;同时忽略汛期暴雨时段的蒸发和下渗作用,以消除蒸散发观测数据缺乏的影响。同时,引入实时校正方法,依据《水文预报情报规范》得到新安江模型和水箱模型模拟马家沟水库流域次洪过程的最优参数,见表3。

表3 新安江模型和水箱模型次洪模拟的优化参数

2.2.2次洪模拟结果分析

引入实时校正后,新安江模型和水箱模型率定期、验证期次洪过程模拟精度评定结果,见表4。

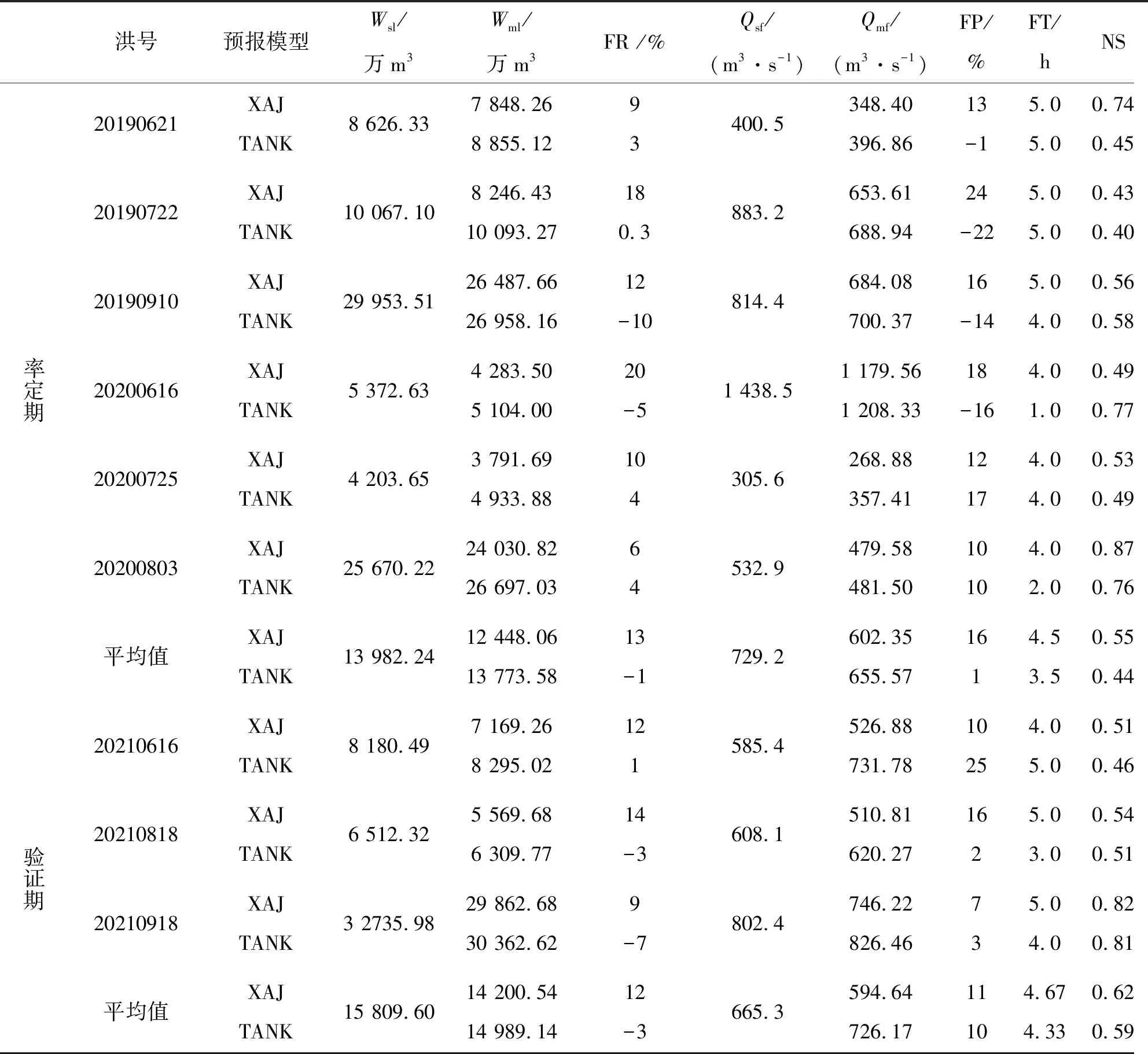
表4 新安江模型和水箱模型次洪率定期与验证期模拟结果

新安江模型和水箱模型均能较好地模拟次洪过程,洪量和洪峰均能基本满足水文预报要求(表4)。其中,率定期间,新安江模型洪量相对误差最大值为20%,平均相对误差为13%;洪峰相对误差最大值为24%,平均相对误差为13%;NS效率系数的最大、最小值分别为0.87、0.43,平均值为0.55。水箱模型洪量相对误差最大值为10%,平均相对误差为1%;洪峰相对误差最大值为16.9%,平均相对误差为13%;NS效率系数的最大、最小值分别为0.86、0.40,平均值为0.44。验证期间,新安江模型洪量相对误差最大值为14%,平均相对误差为12%;洪峰相对误差最大值为16%,平均相对误差为11%;NS效率系数的最大、最小值分别为0.82、0.51,平均值为0.62。水箱模型洪量相对误差最大值为7%,平均相对误差为3%;洪峰相对误差最大值为25%,平均相对误差为10%;NS效率系数的最大、最小值分别为0.81、0.46,平均值为0.59。模型峰现时差均在5 h以内,这与模型设置时引入3 h的实时校正有关,整体来看,9场洪水均能基本满足预报合格标准。

为进一步描述2种模型在马家沟水库流域次洪模拟中的适用性,选择4场洪水表征其洪水过程,洪号分别为20190722、20200803、20210818、20210918,其中20190722、20210818是单式洪峰,过程陡涨陡落;20200803、20210918是受秋淋连阴雨影响的复式洪峰,模拟洪水过程见图 3。

新安江模型和水箱模型均能较好地模拟场次洪水过程(图3)。新安江模型模拟的次洪过程相较水箱模型更平滑,但水箱模型更贴近实测流量过程。水箱模型模拟四场洪水的整体效果更好,洪量、洪峰甚至峰现时间的表现均优于新安江模型,其中模拟20190722、20210818(单式洪峰)的洪量、洪峰相对误差以及峰现时间分别为0.3%、22%、4 h和3%、2%、3 h;模拟20200803、20210918(复式洪峰)的洪量、洪峰相对误差以及峰现时间分别为4%、10%、2h和7%、3%、4 h;总体来看,单峰洪水的模拟效果优于多峰洪水。

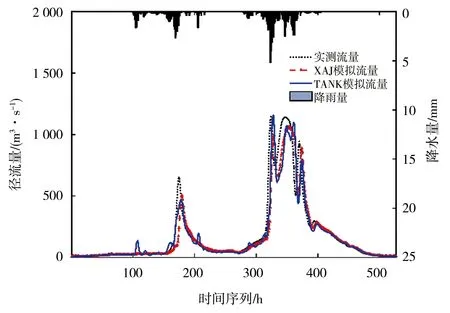
a)20190722

3 结论

研究新安江模型和水箱模型在马家沟水库洪水预报中的适应性,不仅对洪水预报模型选择有一定的参考作用,而且对流域抗洪措施的制定、减少洪灾损失危害具有重要意义。主要结论如下。

a)日模方面,水箱模型的模拟效果更优,洪量相对误差,洪峰相对误差、峰现时差和NS效率系数等4项指标均达到了水文情报预报规范的评定精度要求;次模方面,新安江模型的模拟效果更平滑,水箱模型的洪量、洪峰以及NS效率系数的评定精度更高,更适合马家沟水库流域。

b)集总概念式模型将流域作为一个整体单元进行模拟,未充分考虑模型输入数据的空间分散性和不均匀性,对流域径流的预报会造成一定影响。尽管泰森多边形方法可充分考虑降雨站点中心对雨量空间分布的影响,但采用泰森多边形计算面降雨会坦化局部雨量站降雨峰值的影响,导致洪水预报结果出现一定偏差。

c)为提高预报结果的准确性和有效性,后续将强化以测补报,根据前期汛情灾情检视雨水情监测站点布设是否满足防御要求,滚动修订模型,并考虑引入分布式水文模型,不断提高智能预报水平。