含水致密气藏产能评价新方法——以鄂尔多斯盆地东缘致密气田为例

李 昊, 房茂军, 樊伟鹏, 孙立春, 白玉湖, 齐 宇, 樊冬艳

(1.中海油研究总院有限责任公司, 北京 100028; 2.中国石油大学(华东) 石油工程学院, 山东 青岛 266580)

近年常规油气资源品质下降以及勘探开发技术的快速发展,非常规油气尤其是致密气资源实现规模高效开发,成为油气资源增储上产的主力军[1-3]。随着鄂尔多斯大气区扩边滚动勘探的深入,中海油临兴-神府区块致密气勘探取得突破,发现探明储量超千亿立方米的致密气田[4-5],如何针对临兴-神府区块致密气产能进行准确评价对区块的高效开发意义重大。

由于地质条件与成藏差异[6],鄂尔多斯盆地东缘致密气田相对于苏里格、大牛地等气田呈现出地层压力低、产水量大等特点。另一方面,致密气开发需要水力压裂[7-10],水力裂缝与基质相互作用增加了该类气藏产能评价的难度。李元生等[11]建立了考虑拟启动压力梯度和气水高速非达西效应的气水两相产能方程,并研究了含水饱和度对气井产能的影响。王香增等[12]建立考虑水力裂缝与基质时变效应的致密气产能评价模型,利用该模型对延安气田进行评价研究发现,时变效应对于气井产能影响较大。杨朝蓬等[13]采用气泡法与压差流量法研究发现致密气启动压力梯度并非定值。傅建斌[14]将致密气藏分为压裂措施区和非措施区,并建立不同区域内的致密气藏压裂井产能预测方法,研究发现压裂增产是气井产能上升的主要原因。综上所述,含水致密气藏启动压力梯度与水力裂缝对气井产能影响较大,然而目前针对鄂尔多斯东缘致密气藏综合考虑启动压力梯度致密气压裂井产能评价方法仍待研究。

本文首先基于对鄂尔多斯东缘致密气藏钻井岩心进行启动压力梯度实验研究,创新定量评价启动压力梯度影响因素。结合气水两相渗流理论,创新建立考虑动态启动压力梯度的含水致密气藏压裂气井多因素产能评价方法,为鄂尔多斯东缘致密气藏高效开发提供指导。

1 启动压力梯度实验研究

致密气藏岩石中束缚水饱和度较高,由于岩石亲水,一旦某孔隙喉道被水占据,气体必须克服气水界面产生的毛管阻力才能通过。因此,气体在高含水地层流动存在启动压力(即阈压)[15]。启动压力与含水饱和度的大小及岩石渗透率等有关,也是产能评价中需要考虑的参数。通过测试地层条件下不同渗透率级别的钻井岩心在不同含水饱和度下气相最小启动压力梯度,得出气体启动压力与含水饱和度、岩石渗透率之间的定量关系。

1.1 实验研究步骤

本次实验利用气泡法测量岩心启动压力梯度,实验岩心物性参数见表1,具体实验流程如图1所示。

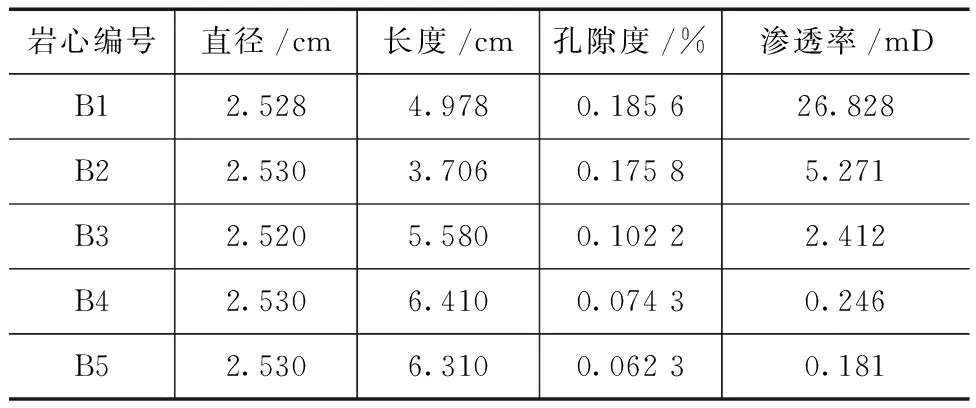
表1 启动压力梯度定量评价实验岩心物性参数

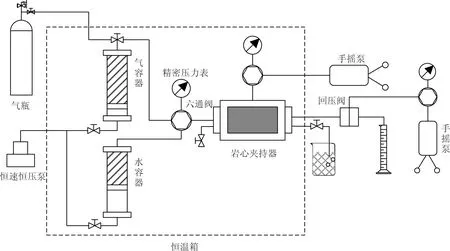
图1 启动压力梯度定量评价实验流程

1)将岩心抽空饱和地层水后,装入岩心夹持器,恒温箱温度设置为地层温度48 ℃,出口端回压阀压力设置为地层压力15 MPa,定压气驱至某一含水饱和度,关闭上游气源,稳定24 h。

2)将出口端回压逐渐降压至0 MPa,然后将出口管线放入装满水的烧杯中。

3)打开上游气源,逐级增加气体压力(0.05 kPa、0.06 kPa、…),每个压力下稳定5 h,直至出口有气泡出现,上游压力即为真实启动压力。

4)增加气驱压力,重复步骤1)～步骤3),测定不同含水饱和度与渗透率下岩心的启动压力。

5) 绘制启动压力梯度关系曲线。

1.2 实验结果分析

本次实验共测试5块不同渗透率与含水饱和度下岩心启动压力梯度,实验结果如图2所示。由图2可以看出,对于同一块岩心下渗透率一定时,启动压力梯度与含水饱和度呈幂函数关系,即随含水饱和度增加,启动压力梯度迅速增加;当含水饱和度一定时,不同岩心渗透率与启动压力梯度呈负相关,即随岩心渗透率增加,启动压力梯度减小。

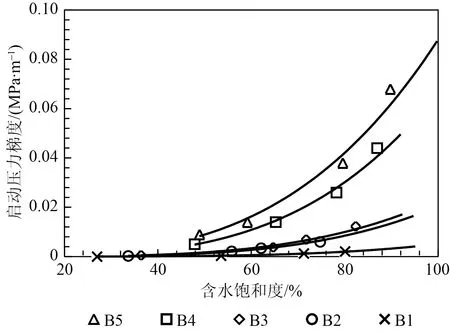
图2 不同渗透率岩心启动压力梯度与含水饱和度关系曲线

进一步定量评价启动压力梯度关系,启动压力梯度与含水饱和度幂指数关系为

式中:λg为气相启动压力梯度,Pa/m;Sw为含水饱和度;a、b为拟合参数。

通过对5块岩心实验数据进行拟合,得到不同渗透率岩心启动压力梯度曲线拟合参数a和b。通过绘制岩心渗透率与拟合参数a和b关系曲线,如图3所示,可得拟合参数a和b与岩心渗透率关系式为

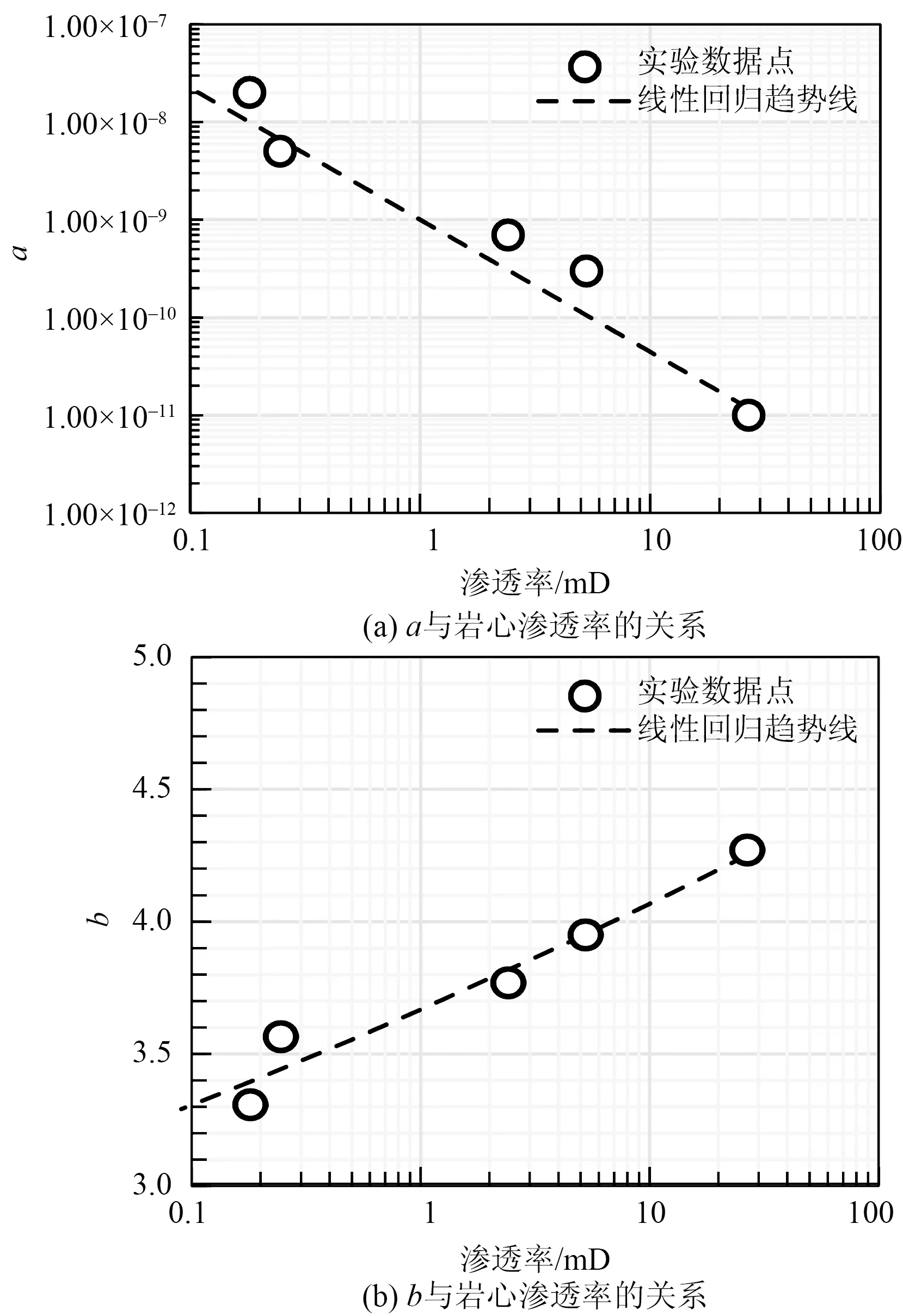
图3 拟合参数a 和b与岩心渗透率关系曲线

a=1×10-9k1.351

(2)

b=3.67k0.045

(3)

式中:k为岩心渗透率,m2。

将式(2)和式(3)代入式(1)可得

式(4)即为鄂尔多斯东缘致密气藏启动压力梯度公式。在实际地层条件下,启动压力梯度并不是恒定不变的,随着气藏的开采,储层含水饱和度逐渐变化,启动压力梯度随之变化。

2 含水致密气产能方程

基于第1节所得的动态启动压力梯度模型,利用气水两相流渗流力学公式,建立考虑水力压裂的含水致密气藏产能公式,为含水致密气井产能评价提供依据。

2.1 物理模型

假设压裂直井位于有效厚度为h、供给半径为re、边界定压为Pe的圆形气藏中央,且该气藏具有均质同性,井筒半径为rw,井底压力为Pwf。建立压裂直井渗流物理模型,并假设:①该直井裂缝为垂直裂缝,并以井筒为轴对称分布;②裂缝中存在压降,为有限导流;③裂缝剖面为矩形,且高度与储层厚度相等裂缝半长为xf,缝宽为Wf;④地层与裂缝流体均符合等温稳态渗流特征,且气水两相间不存在相互作用;⑤不考虑地层、裂缝污染等情况。

由于流体在基质和裂缝中的渗流情况不同,将压裂直井的渗流过程分为基质到裂缝和裂缝到井筒两个部分,流体在裂缝到井筒过程中为气水两相线性流,可称之为渗流场1区。基质至裂缝间发生的是以井筒为中心的气水两相椭圆流,为渗流场2区,如图4所示。

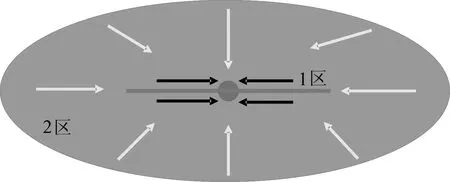
图4 平面渗流场示意图

2.2 数学模型

2.2.1 裂缝中的产能方程推导

考虑气体非达西流动的气相渗流方程为

式中:vg为气相渗流速度,m/s;μg为气相黏度,Pa/m;Krg为气相相对渗透率;Kf为裂缝绝对渗透率,m2;ρg为气体密度,kg/m3;ρgsc为地面条件下气体密度,kg/m3;qgsc为地面条件下气产量,kg/m3;wf为裂缝开度,m;x为裂缝长度坐标变量,m;β为描述孔隙介质紊流影响的系数,称为速度系数,m-1,β=常数/Kα。常用的计算公式为β=7.644×1010/K1.5。

不考虑非达西效应的水相渗流方程为

式中:vw为水相渗流速度,m/s;μw为水相黏度,Pa/m;Krw为水相相对渗透率;ρw为水的密度,kg/m3;ρwsc为地面条件下水的密度,kg/m3;qwsc为地面条件下水的产量,m3/s。

将气水两相运动方程相加,并整理得到

定义两相拟压力梯度为

定义裂缝水气体积比为

将式(10)和式(11)代入式(9)可得

2.2.2 基岩中的产能方程推导

气井生产时,在渗流场2区将形成以气井为中心的地层基质至垂直裂缝间的地层流体椭圆渗流场,形成共扼等压椭圆柱面及双曲流线簇。

将直角坐标系转换为椭圆坐标,即

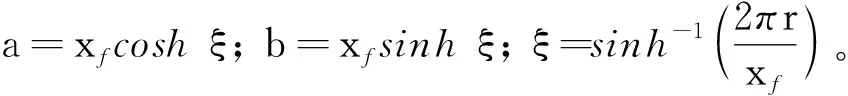
得到的椭圆和双曲线流线簇为

根据扰动椭圆理论,用发展的矩形描述等压椭圆簇,定义平均短半轴为

考虑启动压力梯度与气体非达西流动的气相渗流方程为

式中:λg为气相启动压力梯度,Pa/m;Ki为基岩绝对渗透率,m2。

将气水两相运动方程相加,并整理得到

定义基岩体积水气体积比为

将式(10)和式(20)代入式(19)中可得

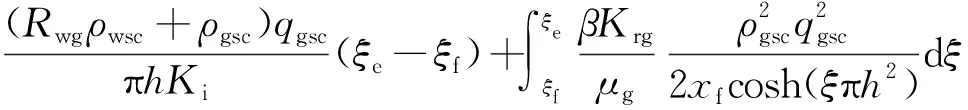
(21)

通过φ(Pf) 将基岩与裂缝中的产能公式联立,得到

进而得到

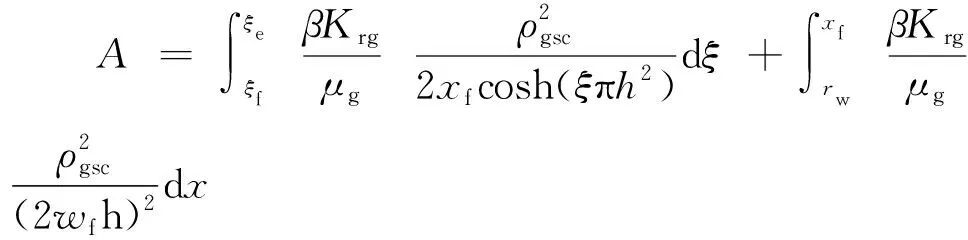
(24)

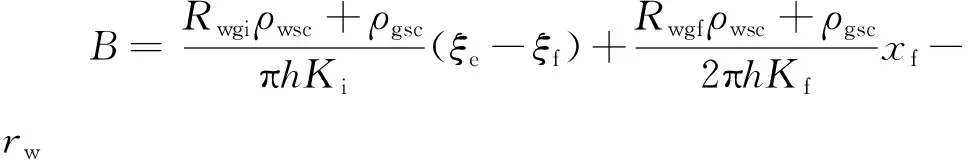
(25)

2.3 模型求解

2.3.1 产能模型求解

根据二项式求根公式,气体产能公式可表示为

利用差分法即可得到A、B、C 3个未知量,即可对气井产量进行求解。

2.3.2 拟压力的求解

研究发现,在气水两相拟压力表达式中,可以将水相的黏度和密度视为常数,式中只有Krg、Krw、μg、ρg是压力的函数,其中气相密度ρg、气相黏度μg与压力P的关系函数关系表达式为

Y=0.2(12-X)

(32)

式中:Mair为空气相对分子质量,kg/kmol;Mg为天然气相对分子质量,kg/kmol;T为温度,K;Z为气体偏差因子;γg为天然气相对密度;K、X为经验系数。

3 实例计算

对第2节所推导的含水致密气藏气水两相稳态产能进行研究,根据鄂尔多斯东缘致密气藏实际地质参数及储层流体的物性对该区的气井产能方程进行求解,并与现场实际试气结果进行对比,结果见表2。研究表明,利用本文建立的产能公式计算的无阻流量与现场实测无阻流量误差较小,5口井无阻流量误差均小于10%,证明了该模型的准确性,也为该区块后续气井产能评价与预测提供依据。

表2 鄂尔多斯东缘致密气藏无阻流量计算对比

4 产能影响因素

在前述的实验研究与产能模型基础上,对影响含水致密气产能的地质与工程影响因素进行分析。

4.1 含水饱和度对产能的影响

根据岩心物性实验结果,分析含水饱和度对产能的影响,结果如图5所示,分别计算含水饱和度Sw为40%、45%、50%、55%、60%下的气井产气流入流出曲线(IPR)。研究发现含水饱和度对气井产能影响显著,随着储层含水饱和度增加,气井产能降低。当储层含水饱和度从40%上升到50%,气井无阻流量下降了51.6%,因此储层含气性的有效预测与评价,对含水致密气藏开发具有至关重要意义。

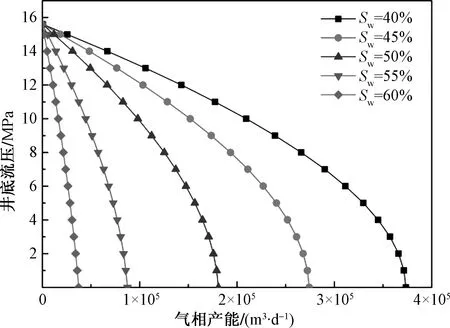
图5 不同含水饱和度Sw下气井IPR曲线

4.2 启动压力梯度对产能的影响

根据岩心物性与启动压力梯度实验结果,在含水饱和度40%～60%区间,分别取启动压力梯度λ为0.003、0.006、0.009、0.012、0.015 MPa/m,分析启动压力梯度对产能的影响,结果如图6所示,随着启动压力梯度增加,气井产能降低,进一步分析在不同启动压力梯度下的该井的最小流动压差(表3)。当启动压力梯度达0.015 MPa/m时,生产压差必须大于7.2 MPa,流体才能开始流动,因此渗透率较小地层需要考虑启动压力梯度的影响。

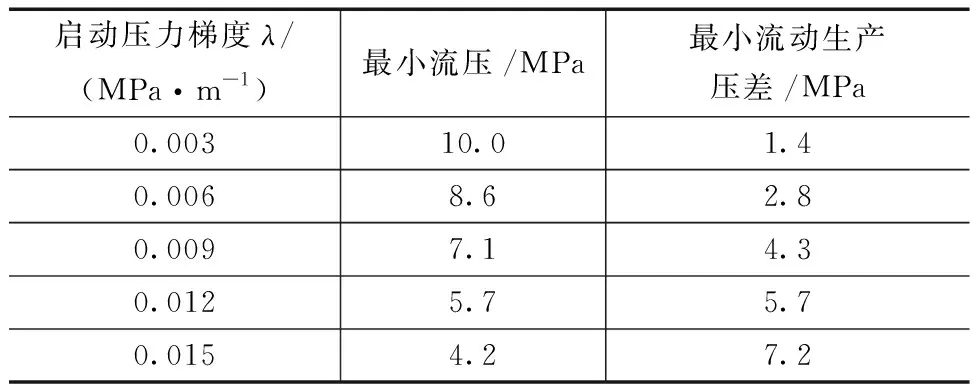
表3 鄂尔多斯东缘致密气藏无阻流量计算对比

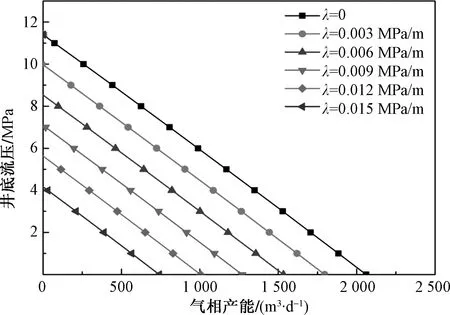
图6 不同启动压力梯度λ下气井IPR曲线

4.3 压裂裂缝半长对产能的影响

依据所推导的压裂直井产能公式,分别设置裂缝半长30、60、90、120 m,得到其气井IPR曲线,如图7所示。由图7可知,随着裂缝半长的增加,气井产能增加,但随着裂缝半长的线性增加,产能增加幅度减小。

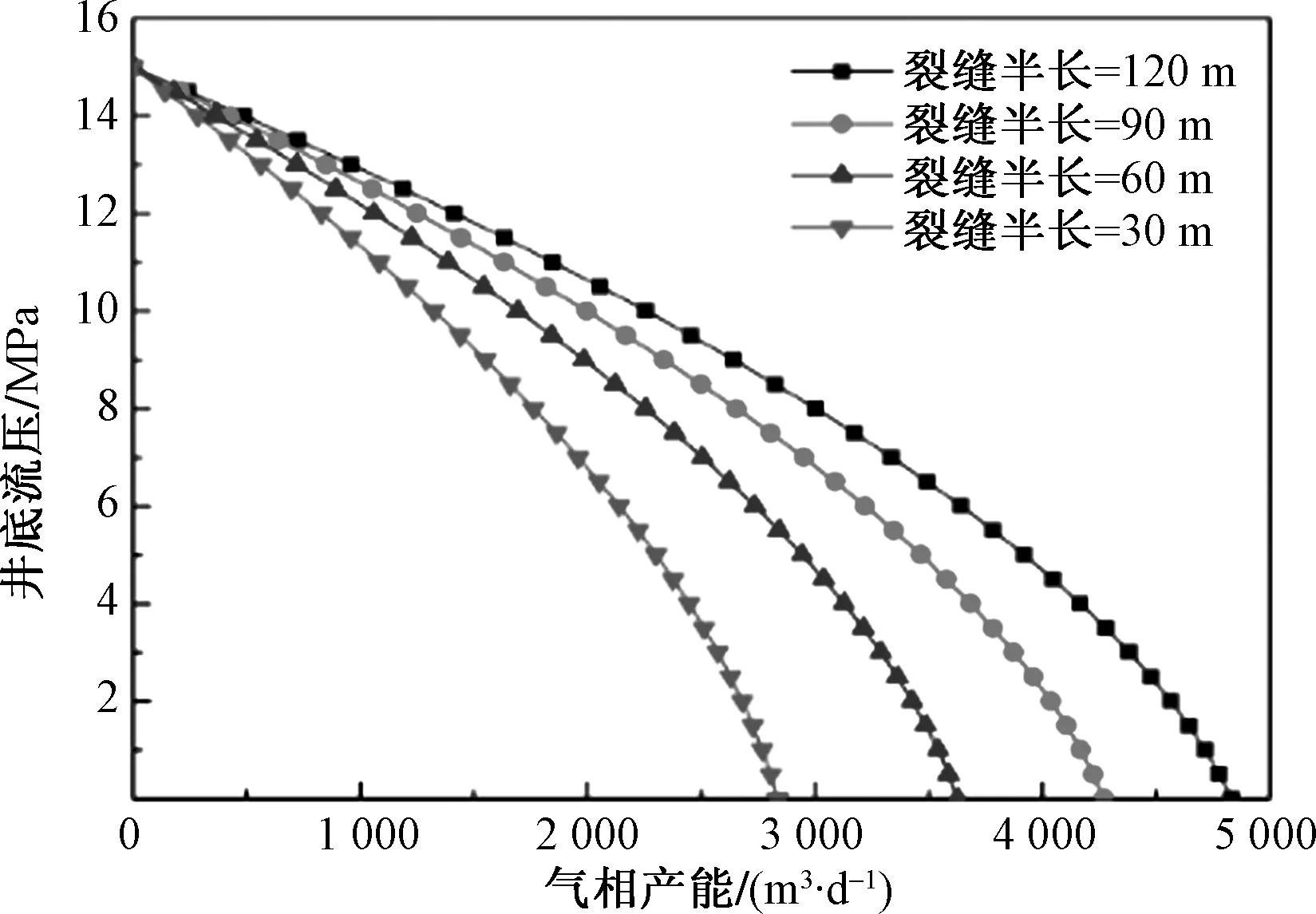
图7 不同裂缝半长下气井IPR曲线

4.4 压裂裂缝渗透率对产能的影响

依据推导的压裂直井产能公式,分别设置裂缝渗透率为100、500、900、1 300 mD得到其气井IPR曲线,如图8所示。由图8可知,随着裂缝渗透率的增加,气井产能增加,但渗透率大于500 mD后,产能增加不明显,说明存在最优的裂缝渗透率值。

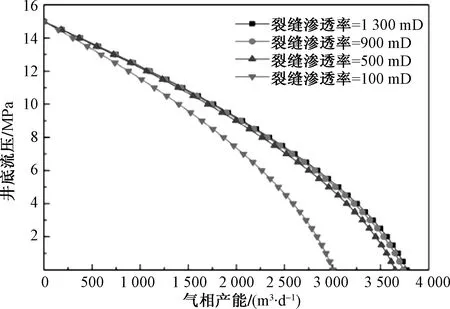
图8 不同裂缝渗透率下气井IPR曲线

5 结论

1)基于鄂尔多斯东缘致密气藏实际岩心实验,创新定量评价了研究区启动压力梯度与储层渗透率和含水饱和度之间关系,研究发现启动压力梯度并不是恒定不变的,随着气藏的开采,储层含水饱和度逐渐变化,启动压力梯度随之变化。

2)在动态启动压力梯度实验基础上,利用气水两相流渗流力学公式,创新建立考虑动态启动压力梯度的含水致密气藏压裂气井多因素产能评价方法,利用建立的产能公式计算的无阻流量与现场实测无阻流量误差均小于10%,证明了该模型的准确性,为该区块后续气井产能评价与预测提供有效的依据。

3)对影响含水致密气藏产能的地质与工程影响因素进行分析研究,发现含水饱和度对气井产能影响显著,随着储层含水饱和度增加,气井产能降低,储层含气性有效预测与评价,对含水致密气藏高效开发具有重要意义;随着启动压力梯度增加,气井产能降低并且气井存在最小流动压差;随着裂缝半长与压裂裂缝渗透率的增加,气井产能增加,但是存在最优的裂缝渗透率值。研究成果为优化致密气工程改造实施提供新的解决方案。