基于改进粒子群算法的指挥所选址优化

李众元，邬建华，陶翰达，徐 鹏，步鑫乐

（1.陆军工程大学，南京 210007；2.武警某训练基地，北京 101500）

0 引言

现代战争对参战双方指挥能力的要求越来越高，指挥所作为指挥员组织实施决策的重要载体，其选址和转移的好坏将直接决定指挥效能。指挥所转移选址问题的关键在于量化影响因素，并且快速计算出选址坐标，综合多种影响因素来计算选址坐标尤为重要。指挥效能是我方需要考虑的首要因素，将指挥对象权重依据其作战任务的重要性赋予指挥权重。在转移过程中，从出发点到目标选址区域的通行状况的因素称为通行因素。敌方兵力部署、敌方火力威胁范围和敌频繁活动区域等称为敌方因素。选址点的气象、水文、地质、地形地貌等自然环境因素，影响野战指挥所开设与施工速度，统称为构工因素。

近年来，对指挥所选址问题的研究，已经取得了些许成果。任保权提出了基于遗传算法的野战指挥所选址问题建模及求解方法，在总结前人选址方法的基础上，构建效能的具体量化指标［1］；杨宇晨基于层次分析法和熵权，对影响后方指挥所选址决策各项指标加以评价分析［2］；文斌等综合运用层次分析法和地理信息系统，针对高原高寒等特殊战场环境下的指挥所选址，进一步量化选址评价指标，提出选址方法和注意事项［3］。由此可见，现有文献对指挥所选址问题的研究还不够充分，没有考虑选址间的联系，且针对转移选址这一问题研究较少。

粒子群优化算法（particle swarm optimization，PSO）在工程领域和科学领域应用广泛，主要解决各种类型非线性复杂优化问题，可最大程度地考虑到多种因素影响力，并根据影响力分布计算出结果，适用于指挥所转移问题。对于粒子群优化算法的研究，目前已经获得了很多的研究成果［4］。虽然粒子群优化算法在选址问题性能较为优越，但其后期收敛速度较慢，容易陷入局部最优［5］，且在指挥所选址问题中，传统的粒子群算法无法考虑选址间的联系。

综上所述，本文着重对指挥所的转移选址进行研究，综合考量生存力与指挥效能两方面的各个因素，结合部队自身实际，根据战局变化，最快选出野战指挥所转移地址，进行设施构筑，为保障指挥机关正常运行提供方法和思路。

1 野战指挥所选址与转移选址模型

根据作战意图、兵力部署、主要方向、开设指挥所的等级和类型等来确定不同的可选址范围，总体上可区分为防御/ 进攻战斗中指挥所的选址与转移、不同等级指挥所的选址与转移、不同类型指挥所的选址与转移等。文中所指的野战指挥所，一般指基本指挥所。

1.1 影响因素

根据文献［1］，影响野战指挥所选址的因素有自然环境因素、战场环境因素、指挥对象因素和其他因素。从野战指挥所的选址开设到转移的全过程来看，其自身生存力与指挥效能一直是需要考虑的两个首要指标。其中，生存力主要由防护与伪装的构筑施工、机动转移能力两者决定；指挥效能主要由指挥对象权重、通信距离和展开地幅决定；战场环境因素主要由敌方兵力部署、敌方火力范围和敌方潜伏出没地域决定，本文用敌方因素指代。

根据实践经验和战术要求，不同的地理环境对指挥所的保障分队的构工能力与机动能力都有不同程度的影响，且还有注意事项：一些地域由于有明显、突出的独立地物，其周边区域极易被敌方发现，应避免选址。

为了简化建模，现将每个满足野战指挥所开设的最小地幅面积，为一个标准单元，把整个选址区域分割成若干个单元，并编码。同时参考文献［6］，将每个单元的地理要素对构工与通行的影响，α（x，y）和（x，y），根据构工与通行的难易程度（便于、较为不便于、非常不便于），分别量化为0.9、0.6、0.3。

针对转移过程，为简化计算，如图1 所示，将保障分队视为一个只有上下左右4 个自由度的粒子。

图1 粒子通行自由度示意图Fig.1 Schematic diagram of particle traffic degrees of freedom

图2 影响度示意图Fig.2 Schematic diagram of impact degrees

假设保障分队通过每个单元区域的理想时间为t，则在现实中通过每个单元的实际通过时间为t实际=t/（x，y），（x，y）为路径上单元的通行因素影响值，单条路线的通行时间为。并根据时效性最优原则，选择通行时间最短的一条路线。

1.2 指挥所选址与转移选址的数学模型

根据野战指挥所选址的影响因素，将一些影响较小的因素转化为约束条件，选择主要的影响因素作为适应度函数，建立数学模型。

1.2.1 约束条件

前文分析得出，野战指挥所远离敌方活动区域，且远离敌直瞄重型火器打击威胁，距离取7 km；我方野战指挥所的选址要确保能够指挥到所有指挥对象，同时要侧重于主攻方向或主要防守方向，本文统一设“距离/指挥权重”应小于12 km，则选址地点必须满足约束条件：

1）距敌距离：

其中，（xi，yi）为野战指挥所选址坐标点；（xk，yk）为敌方活动区域。

2）我方约束条件：

其中，（xj，yj）为指挥对象坐标；βt为指挥权重。

3）根据注意事项，同时出于伪装考虑，应当避开含有独立地物的区域。

1.2.2 战斗准备阶段的选址模型

在战斗准备阶段，保障分队通常具有较为充裕的时间进行机动和施工，参考文献［1］，此时重点考虑指挥效能，在满足约束条件的前提下，考虑指挥对象的指挥权重，靠近重要指挥对象，追求整体指挥通行距离最短，所以该阶段的选址模型，即适应度函数为：

其中，（xi，yi）为选址坐标点；（xj，yj）为指挥对象坐标点；βt为对应指挥对象的指挥权重。

1.2.3 战斗阶段的选址模型与路径规划

其中，α（x，y）为对应选址坐标点的施工因素影响值。

假设T构=200 t，出发点为战斗准备阶段的野战指挥所选址点。

通过寻找满足约束条件，且总时间（通行时间和施工时间）最少的转移地点，并标记好通过的相应路径，即为符合野战指挥所转移选址模型最优的通行路径。

2 粒子群算法及其改进

粒子群算法是一种模仿鸟群觅食的进化算法。将指挥所的选址看作是鸟群在飞行中寻找的食物，将指挥所的选址范围看作是鸟群觅食的范围。若将每只鸟抽象为粒子，则每个粒子根据适应值和自身的位置、速度在解空间中进行搜索。

粒子的速度和位置的更新公式如下：

其中，ω 为惯性权重；c1和c2为学习因子；表示第j 次迭代后粒子i 的位置；rand（）表示0 到1 之间的随机数。惯性权重ω 和学习因子c1、c2通常取固定值，但由于本课题的针对性，对这3 个参数进行优化。考虑到指挥所备选址间的联系，本文根据备选点影响力关系优化粒子初始化、粒子位置迭代公式。

2.1 粒子初始化

本文考虑到指挥所可能的选址之间的影响力关系，以及指挥所可能选址的相似性，提出两个概念：

阮亭云： 屡于《盘山志》搜得未收诗文，奉寄可称快事。 ……《山志》序草成一稿，请正。 愧不能工……甘心受劳受苦，绝不退悔。[3]136

选址相似性sim（u，v）。代表选址u，v 之间的相似性。

其中，Nu和Nv分别代表节点u，v 的邻居节点，也就是当前指挥所和邻近选址的关联情况。

选址之间影响力δ。代表在可能的选址中，各个选址之间相互的影响力。

其中，du和dv分别代表节点u，v 的度数，即当前选址与其他可能的选址的关联情况。imp（v），imp（u）代表当前节点的重要性。由于在现代战争中，时间效益对战斗胜负的影响至关重要，提高了时间效益会对敌方实现信息优势。因此，将imp 表示为该选址的重要程度，主要是该选址区域的构工权重系数、通行权重系数与周围指挥权重之和。

其中，周围指挥权重为备选地址周围7 个单元区域内的所有指挥对象权重之和。

在战斗准备阶段，重点考虑指挥效能，实现指挥员与指挥对象的时间效益最优；在战斗阶段，在满足指挥效能、安全转移与构工完善的前提下，实现时间效益最优，保证指挥机关生存能力。dv和imp（v）均衡了选址本身所代表的时间效益程度和选址在众多选址中的结构信息，不仅极大地考虑到了在众多指挥所备选地点之中的相互制衡关系，而且兼顾了单个指挥所的重要程度。以时间效益最优作为判断依据，能够较好地提升指挥所的指挥效能和生存能力。选址间的影响力δ 又考虑到了选址间的相似程度，以多个相似的备选地点中找到最优位置，为高质量完成选址工作提供了先决条件。

由于δ（u，v）包含了所有节点对，即没有相连的选址间也存在影响力，而影响力数值不够规范可能出现选址间影响力出现巨大差异，进而不利于指挥所选址的综合考量。通过下式可计算所有备选选址点的综合影响力，并将此影响力做标准化处理：因此，将δ 做标准化处理：

其中，Nu表示选址u 的相邻选址。通过上式可以将选址间的影响力标准化并计算出全局影响力，通过遍历所有备选选址即可计算出每个选址的影响力大小和重要程度，为之后粒子的迭代更新提供依据。因此，以上方法既可兼顾选址的相邻影响力，又能考虑到单个指挥所选址的重要程度，从而综合考量出一个适合战争准备的选址地点。

2.2 影响度粒子寻优

传统粒子群算法没有考虑目标间的影响力关系，粒子的运动仅通过粒子的速度函数引导，缺乏针对性。通过对粒子群算法的速度迭代更新公式进行完善，以标准化后的粒子的影响度指导粒子的速度：

相比于原始的粒子群算法，通过选址的影响力分布调整粒子速度，综合单个选址的重要程度和选址间的联系后，更新粒子的寻优方向，因此，IPSO 更加具有针对性。

2.3 自适应惯性权重

由于本课题需在不同的构工因素和通行因素的单元内寻优并标记路径，数据量十分巨大。因此，为提升寻有效率，使用递减权重的方法使算法在运算初期，也就是离最优解位置很远的时候，大范围的搜索速度更快，在算法运算后期，接近最优解时，搜索速度不能过快，使粒子群能在局部更加准确地搜索到最优解，公式如下：

其中，k 为当前迭代次数；kmax为迭代次数的最大值；D 为空间维度。惯性权重w 的取值决定算法全局和局部搜索的程度，研究表明，权重w 在［0.4，0.9］之间的平衡效果最好［9］。此外，针对本课题的需求，优化学习因子c1和c2用以平衡粒子多样性和收敛速度。

2.4 动态平衡学习因子

学习因子c1、c2取值的大小关系着PSO 算法的收敛速度和粒子的多样性［10］。由于需要考虑指挥选址的多种因素，因此，需要平衡收敛速度和粒子多样性，具体设置如下：

其中，根据文献［11］设置参数范围，c1max=2.5，c1min=0.1；c2max=3.2，c2min=0.8；k 为当前迭代次数；D 为空间维度；kmax为迭代次数的最大值。综上分析，IPSO 算法流程图如图3 所示。

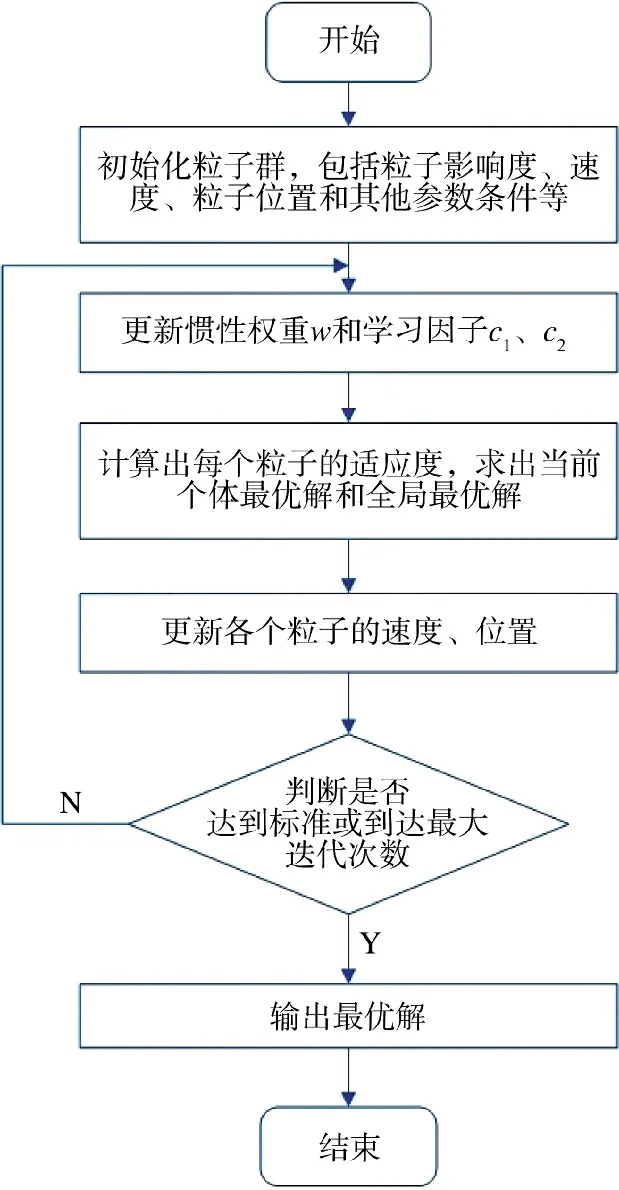
图3 改进粒子群算法流程图Fig.3 Flow chart of improved particle swarm optimization algorithm

3 基于改进粒子群算法的野战指挥所选址仿真

3.1 仿真背景

本文使用Matlab2019 软件，结合部队实战演训中的一般情况，利用文本的数学模型进行实例分析。利用Matlab 程序随机生成每点的施工因素与通行因素如图4、图5 所示。

图5 通行情况示意图Fig.5 Schematic diagram of traffic situation

图4、图5 表示的区域为100×100 个单元。图4 中单元颜色表示保障分队的施工难度，其中，红、黄、绿代表施工困难程度，权重系数分别为0.3、0.6、0.9。图5 中单元颜色表示保障分队的通行难度，其中，红、黄、绿表示保障分队的通行困难程度，权重系数分别为0.3、0.6、0.9。

我方第1 阶段战场态势表现为：我方指挥对象在战斗准备阶段的坐标与指挥权重、敌方活动区域坐标如表1 所示。根据第1 节的分析，以下8 个单元区域（3，16）、（9，45）、（15，27）、（24，35）、（33，60）、（45，53）、（53，42）、（72，64），由于距离桥梁、公路较近、区域内含有独立地物等原因，不予选址考虑。

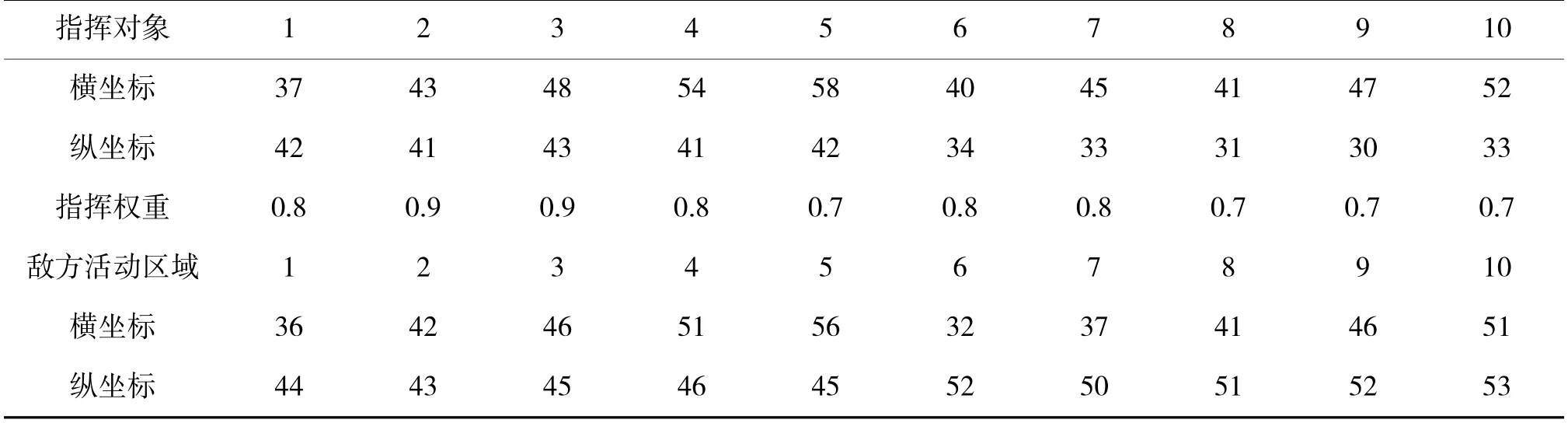
表1 战斗前活动区域坐标Table 1 Coordinates of pre-combat activity area

经过激战后，我部顺利推进，敌方退却，我方准备展开第2 阶段进攻行动。此时，新的战场态势表现为：我方指挥对象在战斗准备阶段的坐标与指挥权重、敌方活动区域坐标如表2 所示。

3.2 模型求解与结果分析

在100×100 的地幅内，粒子群数量取值30，最大迭代次数设为200，惯性权重和学习因子分别采用固定值和本文设定的动态值，使用Matlab 进行仿真。准备阶段选址和转移最优路径选址如图6、图7 所示。

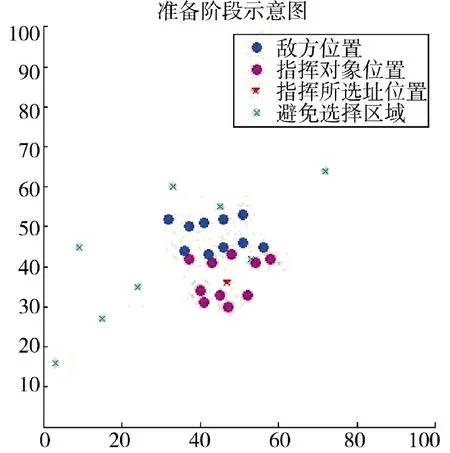
图6 准备阶段选址示意图Fig.6 Schematic diagram of site selection in preparation stage

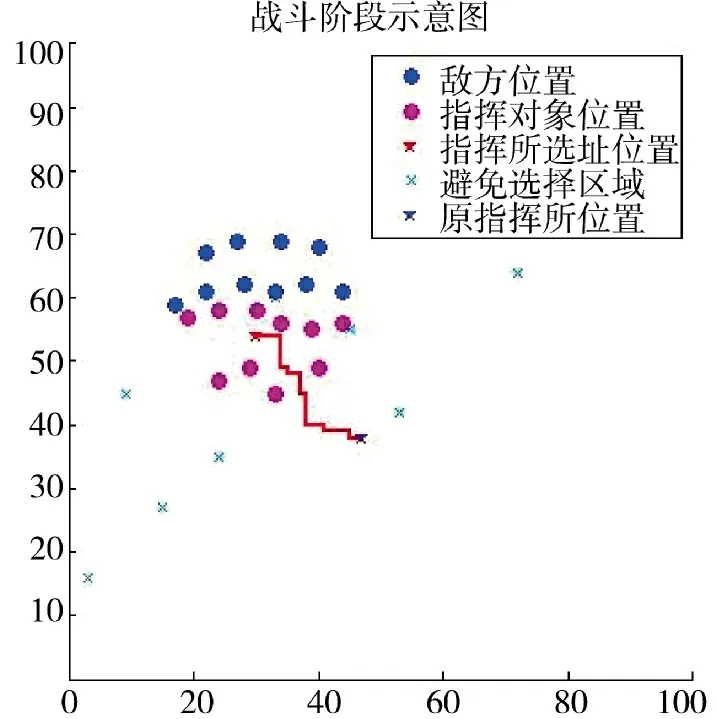
图7 战斗阶段转移选址示意图Fig.7 Schematic diagram of transfer site selection in battle stage

战斗准备阶段和战斗阶段转移选址的目标函数值迭代过程如图8、图9 所示，IPSO 表示本文提出的改进粒子群算法，PSO 表示传统粒子群算法，PSO1 和PSO2 分别表示文献［13-14］的改进粒子群算法，横轴为运算迭代次数，纵轴为适应度函数值，即每次迭代的最优适应度。在战斗准备阶段，PSO求得适应度为112.69，PSO1 求得适应度值为60.89，PSO2 求得适应度值为60.96，IPSO 求得适应度为59.75，确定野战指挥所的最优选址地域为（47，38）。野战指挥所开始转移后，PSO 求得的适应度值为690.69，PSO1 求得适应度值为653.29，PSO2 求得适应度值为653.27，IPSO 求得适应度值为651.59，新的最优选址地点为（30，54）。

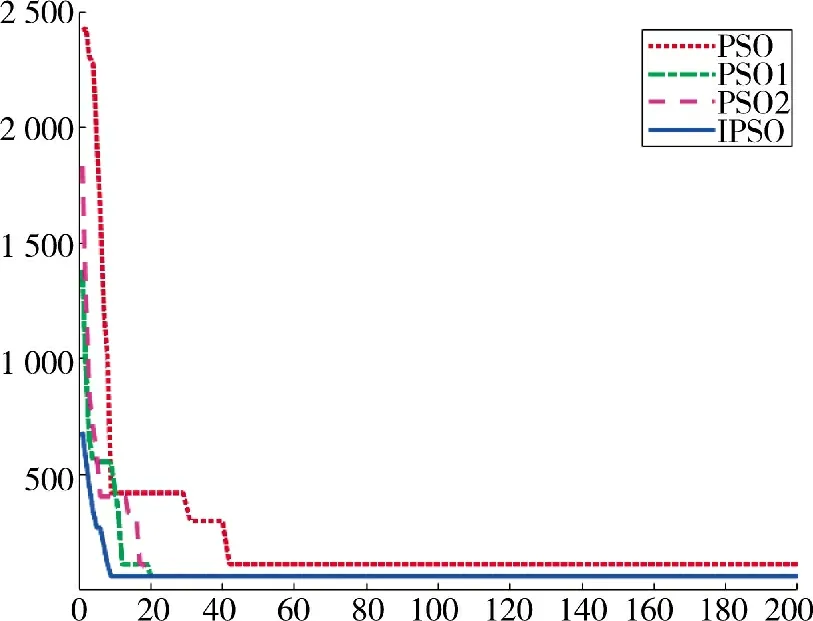
图8 准备阶段自适应粒子群优化算法迭代过程示意图Fig.8 Schematic diagram of iterative process of adaptive particle swarm optimization algorithm in preparation stage

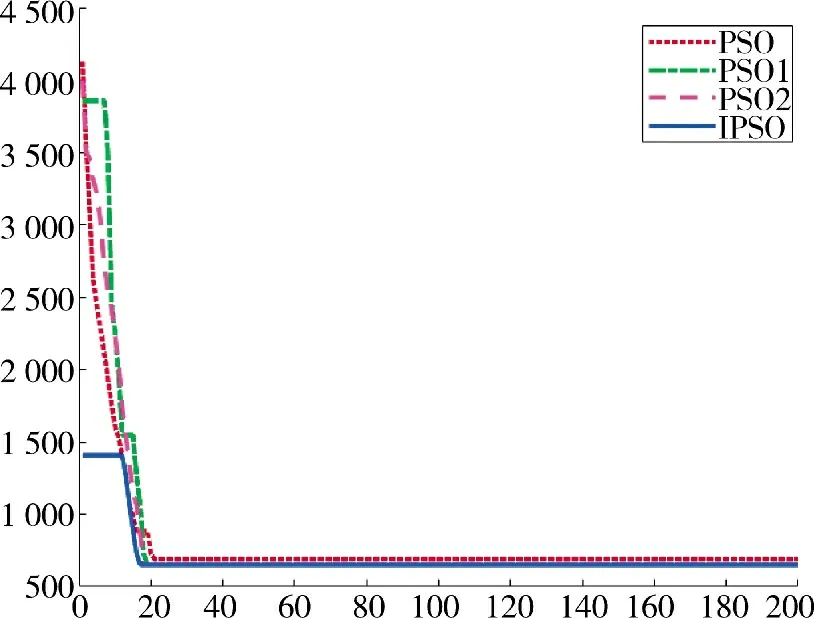
图9 战斗阶段自适应粒子群优化算法迭代过程示意图Fig.9 Schematic diagram of iterative process of adaptive particle swarm optimization algorithm in combat phase

由于备选址地点考虑到了选址间影响度，因此，本文提出的IPSO 算法更具有针对性，表现在图8 中，IPSO 的初始适应度值为592.15，明显优于传统PSO 算法和其他改进的PSO 算法。由于指挥所选址需要综合考虑备选点之间和选址的时间效益，而传统PSO 算法和其他改进的PSO 算法不能有效针对指挥所选址问题，无法考虑到选址间的影响和选址本身的重要程度，仅仅通过局部搜索计算出选址位置，随着PSO 算法的运行，原始的方法已经很难区分不同粒子的区别，表现为图8 的过程：PSO、PSO1、PSO2 的迭代次数均少于IPSO，如若迭代次数较少，则较大概率错过全局最优值。IPSO 针对指挥所选址问题，从开始优选粒子的过程就进行综合考量，不仅兼顾了备选点之间的内在联系，而且考虑到了选址本身的重要程度，从而实现收敛速度和算法精度的提升。针对指挥所选址参考因素多的问题，本文设置动态惯性权重和平衡学习因子，兼顾了粒子的多样性和算法收敛速度，表现在图8 中即IPSO 实现了快速收敛且精度优于其他PSO 算法，证明通过自适应惯性权重和动态平衡学习因子可以对提升算法寻优的收敛速度与精度，并避免陷入局部最优。

战斗阶段的仿真过程如下页图9 所示。虽然IPSO 的初始适应度值已经比PSO、PSO1、PSO2 更优，但由于选址和路径优化过程运算量较大，在前11 代更新中，适应度数值一直处于停滞状态。随着算法迭代，惯性权重、学习因子经历数次变化，IPSO算法跳出了局部最优，适应度值快速下降，在第16代收敛，而PSO、PSO1、PSO2 的迭代次数均高于IPSO 算法。由于PSO1、PSO2 算法对惯性权重和学习因子的优化，适应大运算量的情况，PSO1、PSO2在跳出局部极值后快速收敛，最终迭代次数低于PSO 算法，避免了算法陷入局部最优。IPSO 算法使用指挥所影响力指导粒子位置，因此，更具有针对性，表现在图9 中，即为IPSO 的初始值、收敛速度与精度更优于PSO1 和PSO2。图8、图9 都表明了针对指挥所选址问题改进的PSO 算法相较于原始PSO 算法的优越性。在实际选址中，在初步的工程侦察基础上，还需对备选地址和机动路线进行实时监测和多次评估，确保野战指挥所的转移过程安全顺利。

4 结论

本文针对指挥所选址这一复杂问题，综合考量影响指挥所选址的因素，将作战地域编码，确定约束条件与适应度函数，充分考虑地形影响，分级量化影响程度，最终进行建模与求解，为此类选址问题提供了思路与方法；相较于传统粒子群算法，本文的改进粒子群算法针对指挥所选址问题，从备选址间影响力、算法运算量、粒子多样性和算法收敛速度出发，通过运用相似性函数等进行粒子初始化、利用影响度函数约束粒子迭代、调整惯性权重和学习因子等方式，改进了自适应粒子群算法，针对性地对粒子群算法进行了优化，在准备阶段与转移阶段都取得了不同程度的选址优化结果，但算法改进针对性较强，有一定的局限性。虽然实际运用中还需进一步细化地理要素与指挥相关要素，但对军事行动中野战指挥所的选址与转移提供决策支撑，并为类似的多约束的选址与路径规划问题提供参考。