基于机器学习的轻质低膨胀幕墙玻璃组分设计研究

田 静,黄依平,苗恩新,李 苑,刘军波,张本涛,刘 涌,韩高荣

(1.浙江大学材料科学与工程学院硅材料国家重点实验室,杭州 310027;2.中国建筑第四工程局有限公司, 广州 510665)

0 引 言

传统玻璃幕墙主要采用钢化、夹胶处理的平板玻璃。随着建筑设计美学及功能要求的变化,线膨胀系数高达90×10-7℃-1的普通浮法玻璃难以满足超厚玻璃幕墙对玻璃材料的要求。为获得更低线膨胀系数的玻璃材料,通常采用以下解决方案:1)制造微晶玻璃[1],如以β-石英晶体为主晶相的商用Li2O-Al2O3-SiO2系微晶玻璃具有几乎为零的线膨胀系数,但是低成本、均匀、可见光透明的大尺寸微晶玻璃生产极为困难[2];2)制造TiO2-SiO2二元体系玻璃,如美国康宁公司开发的ULE®玻璃(ultra low expansion glass),它在5～35 ℃几乎没有任何尺寸变化,成为半导体工业[3]及天文学领域[4]的首选材料,但该类玻璃对原料纯度要求极高,难以实现低成本制造;3)制造硼硅酸盐体系玻璃,硼硅酸盐玻璃与普通浮法玻璃相比具有更低的密度和线膨胀系数,如“派来克斯”玻璃,虽然它具有良好的热稳定性、化学稳定性和机械性能[5],但是必须对其组分与密度、线膨胀系数、弹性模量等进行适配性优化,才能满足玻璃幕墙应用的实际需求。

组分与性能关系的定量化预测一直是玻璃研究领域的难点和热点。为了解决这个问题,早前的研究者们[6-8]提出了一些基于玻璃性能随组分变化线性加和的简单经验模型,通过玻璃组分和获得的性能计算系数来粗略预测玻璃的性能,这些模型通常经验性较强,往往只适用于一些特定的体系,且不同研究者提出的性能计算系数不同,预测的准确性差。随着技术的进步和研究的深入,一些基于物理模型的玻璃性能预测方法得以建立,例如基于玻璃网络键约束与自由度的拓扑束缚理论[9-10]、基于量子化学的第一性原理计算[11-12]和基于“杠杆原理”的相图模型[13-14]等。其中,基于硫系玻璃和简单二元、三元、四元氧化物玻璃的拓扑束缚理论进行预测时,预测性能局限于线膨胀系数、硬度、脆性系数和玻璃转变温度;基于第一性原理的分子动力学(ab initio molecular dynamics, AIMD)法,相对于经典分子动力学,它不受限于势函数的开发,可以模拟多元体系,但它存在严重的时间空间局限性,限制了这一方法的预测能力;基于“杠杆原理”的相图模型对非线性较强的玻璃性能预测能力不足。可见,这些模型受限于不同体系玻璃的适用性,对于复杂玻璃体系预测的可迁移性和准确性仍有待进一步提高。实际上,只要冷却速率足够大,元素周期表中几乎所有元素都可以形成玻璃,可能的组分多达1052种[15]。同时,玻璃的非晶态特性使其在化学组成上不需要遵循化学计量的要求,因此开发新型玻璃材料时可以探索的组分数量十分庞大。此外,玻璃的非平衡和非遍历特性又使玻璃结构难以用平衡热力学或者统计力学的方法来描述[16],这对传统的试错型和经验型开发方式提出了严峻挑战,亟待引入更快速、更高效的新方法。

随着近年“材料基因组计划”[17]的实施,以机器学习(machine learning)为代表的数据驱动型建模技术快速发展[18-19],并在玻璃研究领域得到了应用[20-21]。目前已报道了诸多玻璃组分和性能预测模型的研究工作,如:Mauro等[22]针对包含851个硅酸盐玻璃样本的数据集,采用人工神经网络(artifical neural network, ANN)算法建立了玻璃组分与玻璃液相线温度的模型;Cassar等[23]采用ANN算法使用大数据集建立了玻璃组分与玻璃转变温度的模型,并对比决策树(decision tree, DT)、K-近邻(K-nearest neighbor, K-NN)和随机森林(random forest, RF)三种算法对玻璃转变温度、液相线温度、弹性模量、线膨胀系数、折射率和阿贝数等六种性能所建立模型的预测效果发现,采用RF算法建立的预测模型在每种性能上都有最好的表现[24];Deng等[25]利用康宁公司收集的大型数据集对氧化物玻璃的密度、弹性模量、剪切模量和泊松比进行了全面的机器学习研究,并对比了RF、K-NN、ANN、支持向量机(support vector machine, SVM)和线性回归LASSO(least absolute shrinkage and selection operator)五种算法,其中LASSO模型对于线性度较好的密度表现最优,而非线性的弹性模量、剪切模量和泊松比则要应用RF、ANN和K-NN等算法才能获得较好的拟合结果;Yang等[26]将高通量分子动力学模拟获得的由231个Ca-Al-Si系玻璃样本组成的数据集作为训练集,对比研究了使用多项式回归、LASSO、RF和ANN四种算法训练的玻璃弹性模量预测模型,其中RF模型表现出最好的非线性拟合能力,ANN模型拥有最好的泛化能力;Hu等[27]同样使用由高通量分子动力学模拟获得的二元、三元硅酸盐玻璃数据集,开发了梯度推进机算法(GBM-LASSO),建立了玻璃组分与密度、体模量和剪切模量的模型;Ravinder等[28]采用高保真的深度神经网络算法在玻璃组分与密度、弹性模量、剪切模量、硬度、玻璃转变温度、线膨胀系数、液相线温度和折射率等八个性能之间建立了预测模型。在众多的机器学习算法中,RF算法具有较好的非线性捕获能力,适用于高维特征空间及大数据集,在各相关工作中都有较好的表现。

本研究针对超厚玻璃幕墙对轻质、低膨胀玻璃材料的性能需求,从SciGlass数据库[29]中提取104规模的数据集,利用随机森林算法构建氧化物玻璃的组分与线膨胀系数、密度和弹性模量三个性能的预测模型,采用SHAP(shapley additive explanation)分析[30]等方法对预测模型进行可解释性研究,并且在硼硅酸盐玻璃的大型组分空间中实现了性能的准确预测和组分的快速筛选,为轻质、低膨胀硼硅酸盐幕墙玻璃组分的设计开发提供新的思路。

1 实 验

1.1 数据集建立

本文所有初始数据均来自SciGlass数据库[29],从中分别提取了玻璃组分及其对应的线膨胀系数、密度和弹性模量,并对数据集进行了数据清洗。

1)无效样本剔除。去除标签值为空的样本和氧元素含量低于30%(原子分数)的样本,确保数据来自有效的氧化物玻璃。

2)输入特征降维。为建立相对完整的预测模型,剔除出现频率极低且含量极少的元素样本,如H、C、N、F、S、Cl、Br、I、Ag、Au、Pt、Ru、Hg等。最终以其余56种元素的氧化物作为输入特征,进行归一化处理并去除重复样本。

3)极端值样本剔除。设定线热膨胀系数、密度和弹性模量的取值区间分别为[0.10,300]×10-7℃-1,[1,10] g/cm3和[1,170] GPa,忽略区间外的样本。

经以上操作后的数据集,含密度数据的样本有62 312个,含线膨胀系数数据的样本有52 073个,含弹性模量数据的样本有13 030个。

1.2 机器学习算法

随机森林(RF)是一个以决策树为基本单元的集成算法[31-33]。本文的RF回归模型以氧化物摩尔组分为输入,相关性能为输出,在训练过程中按照3∶1的比例划分数据集为训练集和测试集,以平均绝对误差(mean absolute error, MAE)和决定系数R2为模型评估指标,定义如式(1)、(2)所示。

(1)

(2)

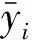
1.3 测试方法

采用熔融-冷却法制备玻璃样品。以分析纯的石英砂、氧化铝、四硼酸钠、碳酸钙、碱式碳酸镁、无水碳酸钠为原料,采用梅特勒ME2002E型精密天平称量玻璃原料,经玛瑙研钵充分混合研磨后放入石英坩埚,随后在宜兴万石JGMT-8/300型高温升降炉中进行玻璃熔制。具体过程为:从室温经过90 min升温至1 000 ℃,再从1 000 ℃经过50 min升温至1 590 ℃,在1 590 ℃保温2 h后又经10 min升温至1 630 ℃,在1 630 ℃保温50 min后经25 min降温至1 560 ℃,玻璃液经黄铜模具成型后,玻璃块体与模具一起在河北雅格隆GW1100-50型箱式电炉中730 ℃下退火1 h后随炉冷却[35]。制得的样品经过切割、打磨和抛光后,采用美国Cetea的Analyte HE型193 nm激光剥蚀(laser Ablation, LA)系统进样与德国Thermofisher的iCAP QR型电感耦合等离子体质谱仪(Inductively Coupled Plasma Mass Spectrometry, ICP-MS)联机的LA-ICP-MS测试样品氧化物组分;采用北京旭辉新锐的MD-100型玻璃密度仪测量样品密度;采用北京旭辉新锐的DIL-1000型膨胀系数测量仪测量样品线膨胀系数,温度范围设置在室温到300 ℃;采用Agilent G200型纳米压痕仪测量样品弹性模量。

2 结果与讨论

2.1 数据集分析

图1为数据集中线膨胀系数(coefficient of linear expansion, CTE)、密度和弹性模量的数据分布情况及三种性能样本的氧化物数量分布情况。图1(a)～(c)分别为样本的线膨胀系数、密度和弹性模量的分布直方图,可以看出,线膨胀系数和密度数据分布具有明显的非对称形状,线膨胀系数的样本点主要分布在(60～120)×10-7℃-1,密度的样本点主要分布在2～3 g/cm3,弹性模量的数据分布近似于正态分布,样本主要分布在50～100 GPa。图1(d)～(f)为样本氧化物数量的分布直方图,对于三种性能来说,三元体系的样本数量均最大,样本数量随氧化物种类的增多显著减少,表明以往的工作更多关注组分简单的玻璃体系。

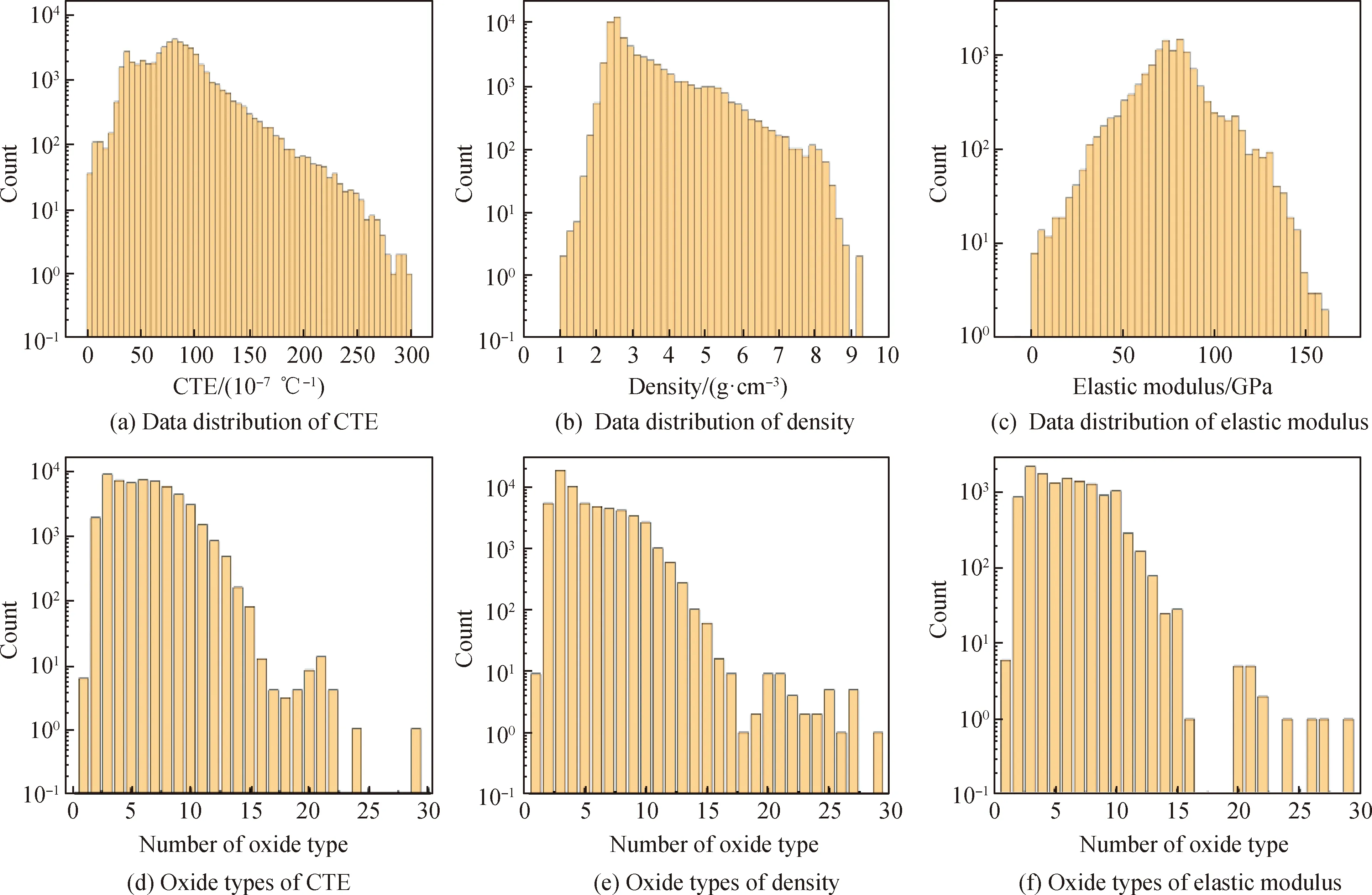
图1 数据集中线膨胀系数、密度和弹性模量的数据分布情况及三种性能数据集样本的氧化物种类分布情况Fig.1 Data distribution of coefficient of linear expansion, density and elastic modulus and distribution of oxide types of three properties in data set

2.2 模型质量分析

图2为建立的RF模型在训练集和测试集上的表现。由图2可见,线膨胀系数、密度和弹性模量的RF模型在训练集上的MAE和R2分别为2.040 0×10-7℃-1和0.988 0,0.037 4 g/cm3和0.994 0,1.297 0 GPa和0.985 6,表明三个模型在训练集上与试验结果具有良好的一致性。RF模型在训练集上对密度的拟合能力优于线膨胀系数和弹性模量,这种差异则可能与样本数量、数据质量、算法拟合能力和性能本身可预测的难易程度有关[1,27,36]。对比三个模型在测试集上的表现,数据分布比训练集更离散,且在测试集上线膨胀系数、密度和弹性模量模型均表现出了高于训练集的MAE,分别为4.500 0×10-7℃-1、0.100 4 g/cm3和3.445 2 GPa,表明模型在泛化迁移过程中发生了一定程度的“失真”。但是考虑到本研究采用了104规模的大样本集合和56个特征的高维输入空间,建立的RF模型仍表现出较好的泛化能力,表明三个模型针对多元组分玻璃的性能预测具有较强的实用性。

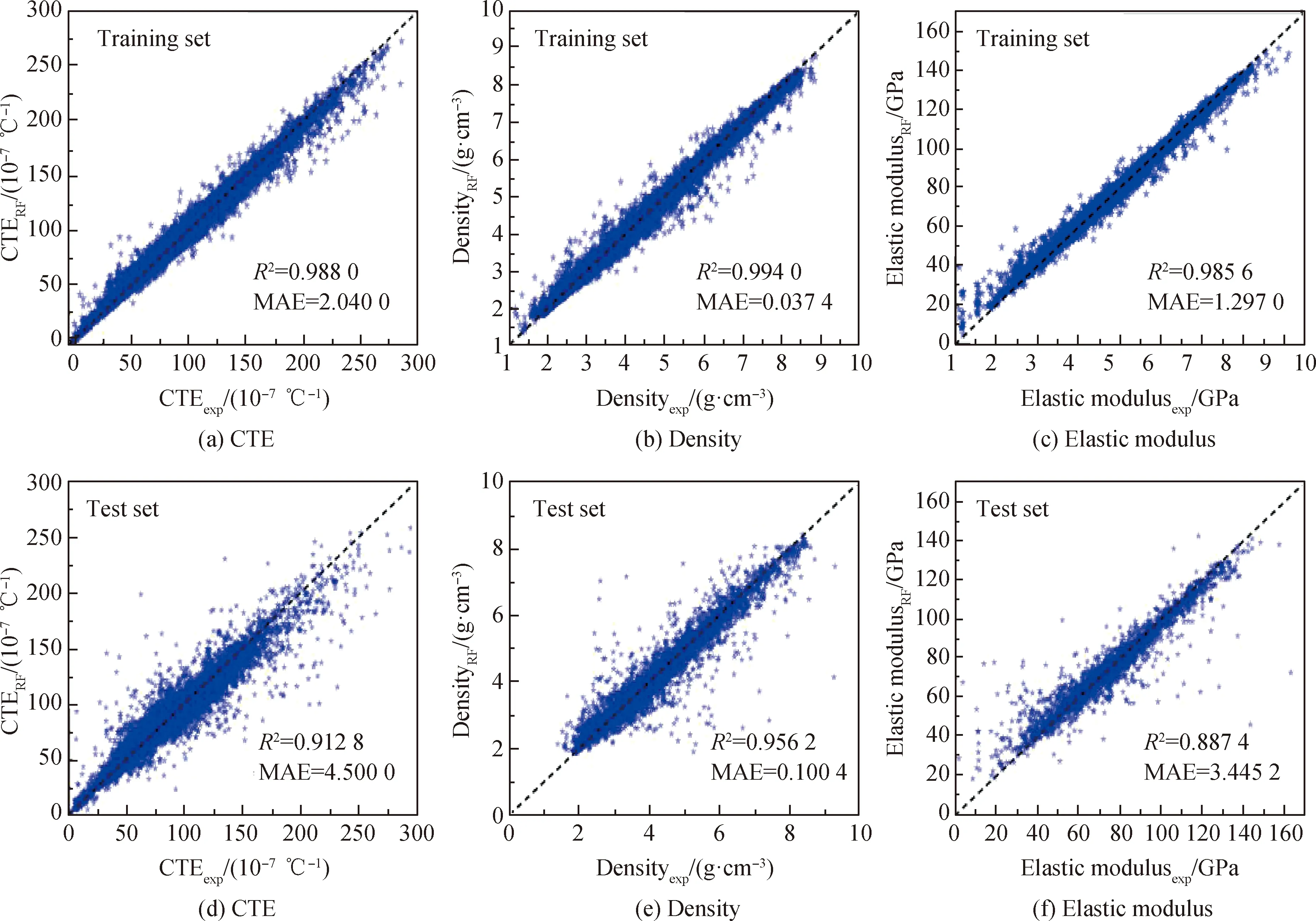
图2 优化后的线膨胀系数、密度和弹性模量模型在训练集和测试集上的表现Fig.2 Performance of optimized coefficient of linear expansion, density and elastic modulus models on training set and test set

为了进一步验证模型的预测能力,利用训练好的模型对文献中报道的样本进行预测[37-42],结果如图3所示。由图3可见,线膨胀系数、密度和弹性模量的预测相对误差分别在±10%、±5%和±5%,表明本文建立的模型可以准确预测不同氧化物玻璃体系的线膨胀系数、密度和弹性模量,满足实际应用的要求。

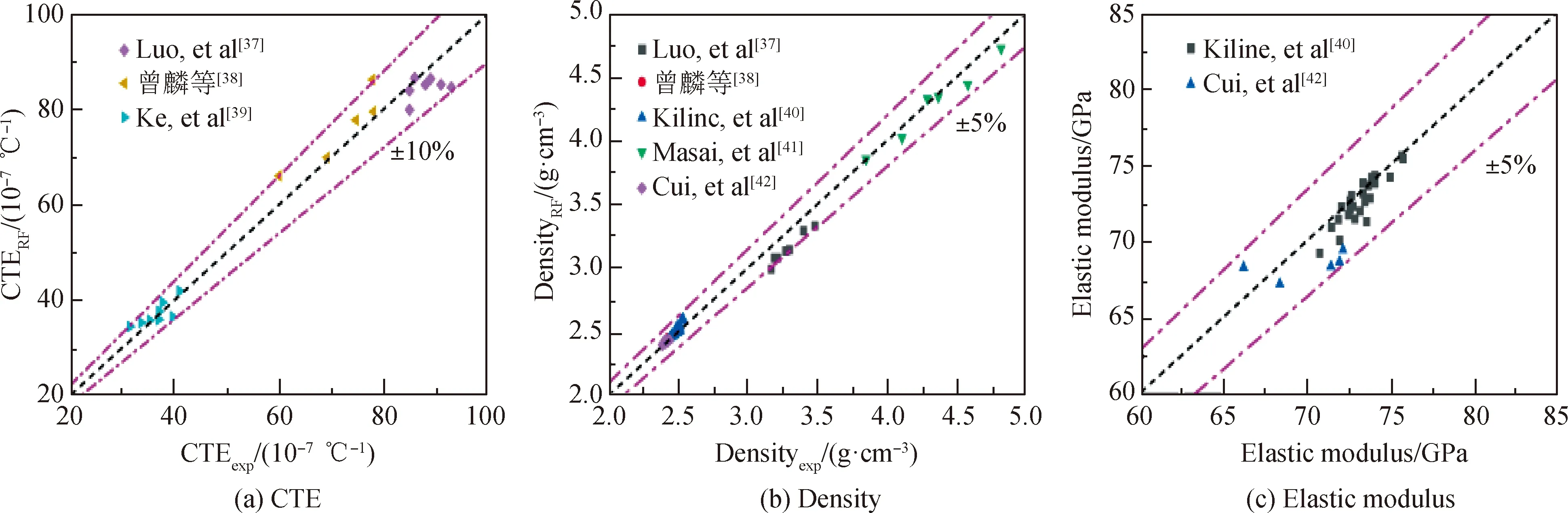
图3 RF模型对文献报道的氧化物玻璃线膨胀系数、密度和弹性模量的预测值和试验值的对比[37-42](点线为相对误差夹线)Fig.3 Comparison between predicted results from RF models and experimental results of coefficient of linear expansion, density and elastic modulus of oxide glass reported by other papers[37-42](the two pink dot-dashed lines are relative deviation lines)

2.3 模型可解释性

随机森林模型的构建完全基于数据,其内部是一个“黑盒”,为了给模型提供一定的可解释性,首先采用特征的置换重要性分析来评估氧化物组分对性能的影响作用[43-44]。置换重要性定义为通过随机打乱某个特征在OOB(out of bag)样本集中的排列顺序来破坏它们与目标值的原始关联,将特征值乱序之前与乱序之后在OOB集上的R2差值作为该特征的重要性,一个特征的置换重要性数值越大,则该特征与模型整体预测精度越相关。RF模型重要性排序在前10的特征(氧化物)在训练集和测试集上的置换重要性表现如图4所示。从图中可以看出:对于线膨胀系数而言,修饰体碱金属氧化物(Na2O、K2O)、网络形成体(SiO2、B2O3)和中间体氧化物(Al2O3)最为重要;对于密度而言,重金属氧化物(Bi2O3、PbO、TeO2)以及网络形成体氧化物(SiO2、B2O3)最为重要;对于弹性模量而言,网络形成体(SiO2、B2O3)、中间体氧化物(Al2O3)以及修饰体碱金属氧化物(Na2O)、碱土金属氧化物(MgO)最为重要,这与基于玻璃化学基础理论的分析是一致的。进一步可以发现,三个模型对部分特征置换重要性的评价在训练集和测试集上不一致,如线膨胀系数和密度模型在训练过程中分别高估Li2O和Na2O的重要性,而弹性模量模型在训练过程中则极大地高估了CaO的作用,对应了弹性模量模型具有最差的泛化能力,与图2结果一致。

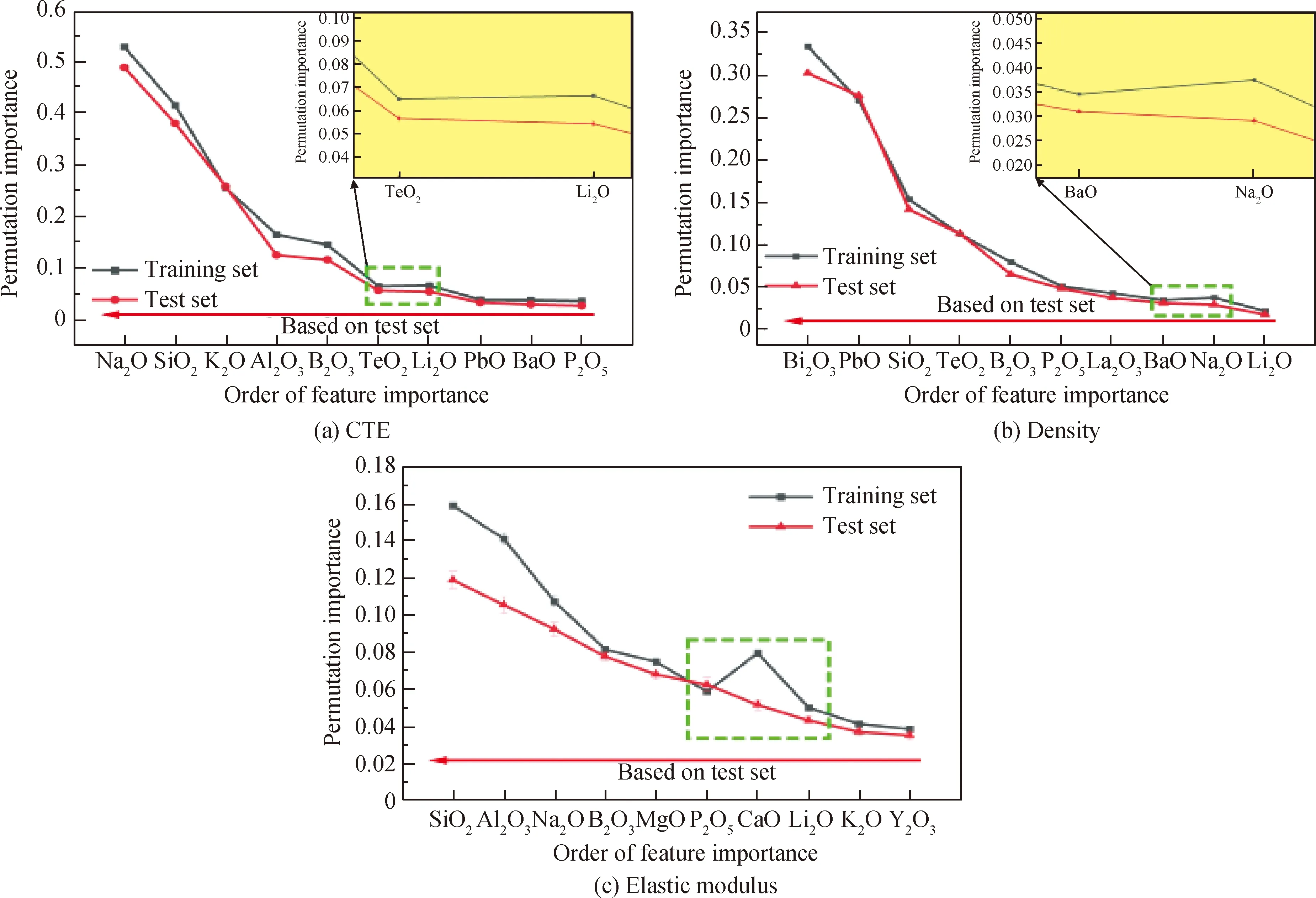
图4 线膨胀系数、密度和弹性模量随机森林回归模型在训练集和测试集上的特征置换重要性分析Fig.4 Feature permutation importance analysis of coefficient of linear expansion, density and elastic modulus random forest regression models on training set and test set

为了在置换特征重要性排序基础上进一步探明氧化物对性能的影响,引入基于合作博弈论个体边缘收益的SHAP分析[45]。三个性能模型的SHAP分析值蜂群图如图5所示。蜂群图的左侧标签为根据特征SHAP值绝对值的平均值进行重要性排序的前10种氧化物,水平轴上的有色点代表包含该氧化物的一个玻璃样本;点的颜色表示该氧化物在样本中的含量,随着右侧色标中的冷色到暖色,对应氧化物含量由小到大;点在x轴的位置代表该氧化物在样本中的SHAP值,具有相同SHAP值的点在垂直方向堆叠。由于SHAP值具有可加和性,即

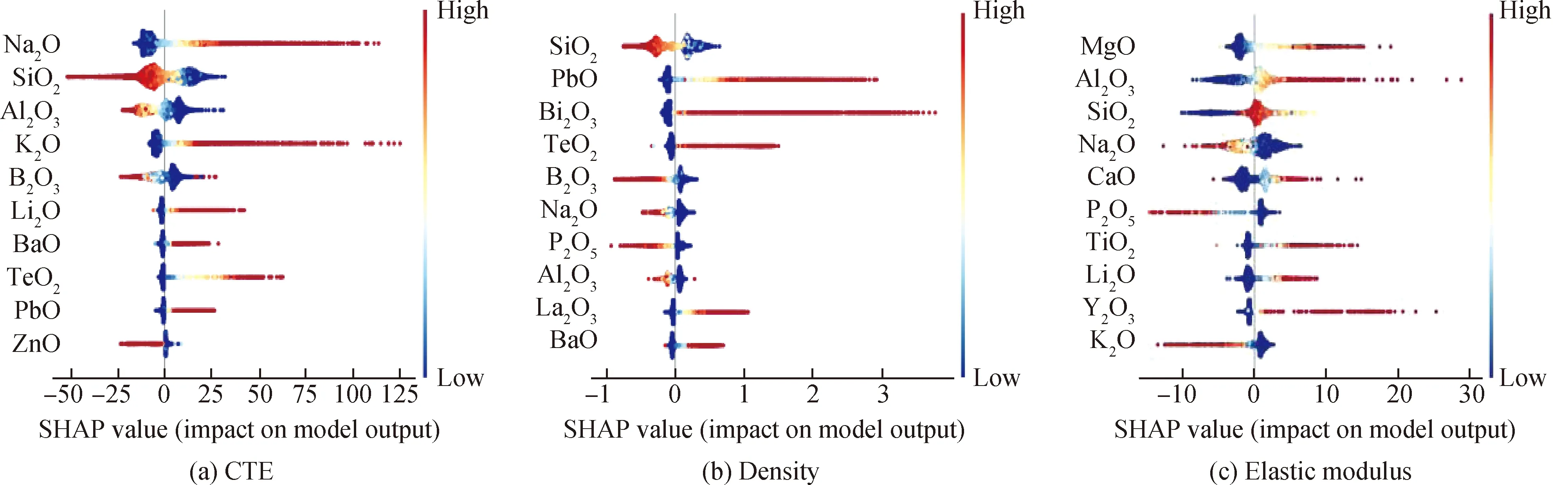
图5 线膨胀系数、密度和弹性模量RF模型SHAP分析值蜂群图Fig.5 Beeswarm plot of SHAP analysis values of coefficient of linear expansion, density and elastic modulus

yi=ybase+f(xi1)+f(xi2)+…+f(xik)

(3)

样本xi中所有特征的SHAP值f(xik)与基础值ybase(目标值的平均值)之和等于该样本的预测值yi,因此SHAP分析可以反映特征对目标的贡献是正向的还是负向的。

如图5(a)所示,对于氧化物玻璃的线膨胀系数,修饰体Na2O、K2O、Li2O和BaO含量的增加将会增加线膨胀系数,形成体以及中间体SiO2、Al2O3、ZnO含量的增加将减小线膨胀系数,但形成体TeO2[46-47]却表现出了相反的作用。此外,PbO作为一种常用的助熔剂,其含量的增加也会导致玻璃线膨胀系数的增大。如图5(b)所示,对于氧化物玻璃的密度,PbO、Bi2O3、TeO2、BaO和La2O3等重金属氧化物含量的增加将增大玻璃密度,对于相对原子质量较低的形成体、修饰体和中间体氧化物SiO2、B2O3、P2O5、Na2O、Li2O、MgO、Al2O3,它们含量的增加将主要减小玻璃的密度。如图5(c)所示,对于氧化物玻璃的弹性模量,形成体和中间体SiO2、Al2O3、MgO、TiO2含量的增加会增大玻璃的弹性模量,但P2O5在玻璃中独特的网络结构决定了高含量的P2O5会减小玻璃的弹性模量。修饰体Na2O和K2O含量的增大将减小玻璃弹性模量,但高阳离子场强的Li2O[36]和Y2O3[48]含量的增加对弹性模量起正向作用,而CaO则表现出一定的两面性。除此之外,在线膨胀系数和弹性模量的SHAP图中均清楚地表现了著名的“硼反常”现象,即B2O3含量的增加既可能增加也可能降低线膨胀系数和弹性模量,与文献[49-50]结论一致。

3 玻璃组分-性能的RF模型应用与试验验证

以硼硅酸盐玻璃六元体系Si-Al-B-Ca-Mg-Na为设计对象,利用前文建立的RF模型在该体系中进行系统性研究和试验验证。限定SiO2的含量在60%～80%(摩尔分数,下同),所有氧化物的含量总和为100%,氧化物组分间隔为1%,由此形成包含1 179 255种玻璃组成的样本空间。用RF模型计算了该样本空间中所有玻璃的线膨胀系数、密度和弹性模量,结果如图6所示,映射图以弹性模量值为色标,累计耗时约38 654 core·s(≈10.7 core·h)。样本点的线膨胀系数主要集中在(30.00～90.00)×10-7℃-1,密度在2.30～2.70 g/cm3,弹性模量在70.00～90.00 GPa。轻质、低膨胀幕墙玻璃要有尽可能低的密度、线膨胀系数和相对适宜的弹性模量,同时考虑到玻璃实际生产涉及的熔融温度、成玻特性等工艺性能,最终在密度低于2.40 g/cm3、线膨胀系数低于60.00×10-7℃-1、SiO2含量为[70,80]%、网络修饰体含量为[10,20]%的区域内挑选了4组硼硅酸盐玻璃组分进行试验验证,所选样本均分布在图6矩形框内。

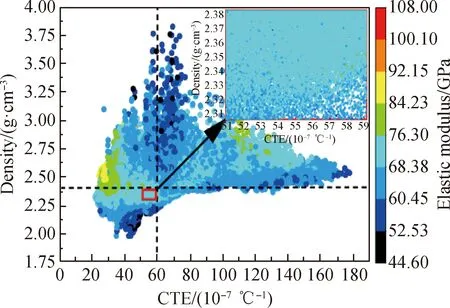
图6 组分空间中各样本点在线膨胀系数-密度面上的二维映射分布Fig.6 2D mapping distribution of data points on coefficient of linear expansion-density plane in composition space

表1为玻璃设计组分与LA-ICP-MS实测组分对比。由于熔制过程中存在原料挥发、坩埚成分渗析等因素的影响,实际组分同设计组分总会有所偏差,一般来说,含量少的组分偏差会相对较大,其中所有样本的SiO2组分偏差均分布在3%以内。图7为样本性能测试值与预测值的对比。四个样本的密度相对偏差均在±1%,线膨胀系数和弹性模量的相对偏差在±5%。这些结果再次印证了本工作建立的RF模型具有足够的准确性,能够在真实世界的高维组分空间中准确预测氧化物玻璃的线膨胀系数、密度和弹性模量。《玻璃幕墙工程技术规范》(JGJ 102—2003)[51]对玻璃幕墙材料弹性模量的规定为0.72×105N/mm2(72.00 GPa),对线膨胀系数的规定为(0.80～1.00)×10-5℃-1((80.00～100.00)×10-7℃-1),对材料重力密度的规定为25.60 kN/m3(2.61 g/cm3)。本文筛选出的四组样品在弹性模量合规的情况下,具有更低的密度和线膨胀系数,提高了玻璃的抗热冲击性能,增加了玻璃本身以及其他连接件和支撑件的使用寿命。

表1 玻璃样品的设计组分与LA-ICP-MS实测组分Table 1 Nominal composition and experimental compositions from LA-ICP-MS of glass samples /%

图7 四个样本的线膨胀系数、密度和弹性模量的试验值与预测值的对比以及基于试验值的相对偏差Fig.7 Comparison between experimental results and predicted results from coefficient of linear expansion, density and elastic modulus models of four samples, and relative deviation based on experimental results

4 结 论

1)本文利用机器学习方法和玻璃材料数据库,在氧化物玻璃组分和线膨胀系数、密度及弹性模量等三项性能之间建立了随机森林预测模型,在包含56种氧化物的高维组分空间中实现了对性能的准确预测。

2)结合随机森林模型的特征重要性分析和SHAP分析进行了模型可解释性研究,复现了氧化物玻璃组分中的硼反常等现象,提高了模型的透明度和可信度。利用该预测模型对Si-Al-B-Ca-Mg-Na六元氧化物组分空间中的约118万个玻璃配方进行快速预测,从中筛选了4组硼硅酸盐玻璃组成,性能的测试结果与模型预测相符,且优于相关规范要求。