基于多模态多目标优化的端元束提取方法研究
2023-07-31林洁雯罗婷文徐志搏
林洁雯 陈 建 罗婷文 徐志搏
(1.自然资源部城市国土资源监测与仿真重点实验室, 深圳 518000;2.自然资源部超大城市自然资源时空大数据分析应用重点实验室, 上海 200063;3.中国农业大学工学院, 北京 100083; 4.深圳市智能微小卫星星座技术与应用重点实验室, 深圳 518107;5.浙江大学能源清洁利用国家重点实验室, 杭州 310027;6.浙江大学浙江省农业智能装备与机器人重点实验室, 杭州 310058)
0 引言
遥感技术已经广泛应用于农业遥感[1-4]、森林监测、生态信息提取、海洋监测等领域。遥感探测器记录的能量与瞬时视场角(IFOV)对应地面单元内地表物质反射或发射的能量有关。但是由于传感器分辨率的限制,导致某一像元中包含多种地物,形成混合像元的现象[5]。通过光谱混合分析可以分解瞬时场角内由一组固定端元混合而成的单个像元的光谱反射率观测值,称为解混。而能够从中提取出来的每一类地物的光谱特征称为端元,它决定了解混的精度。在纯像元假设下,一组高光谱影像同时包含纯像元和混合像元,纯像元中只含有一个端元,混合像元中含有多个端元[6]。人工难以区分和辨认混合像元和纯像元,需通过算法自动提取实现解混。自动端元提取兼具便利性及准确性:①便利性:人工无法确定表达某类地物信息的端元数量,而算法可以自动提取端元的数量。②准确性:人工选择没有标准或指标作为依据,而自动端元提取是根据算法寻优策略和指标(如:均方根误差(RMSE))选择的,提取出的端元能够更接近实测的地物光谱信息,解丰度再反混后更接近原图信息,准确性更强。
遥感影像上同物异谱或同谱异物的现象会造成同一混合像元端元在影像上光谱不唯一,产生光谱变异性[7]。当影像中存在光谱变异现象时,如果只用一条端元光谱表示一类物质的端元,容易造成误差。因此,端元束比单条端元光谱更能反映地物信息。近几年,国内外专家和学者将端元提取研究转向端元束的提取研究。端元束提取方法能够获得每一类物质具有类内光谱变化的若干端元。目前提取端元束的算法相对于端元提取算法较少,现有方法包括分块提取和集群智能算法。分块提取方式将截取的像素块通过随机(EBE)[8]、局部提取(LLG)[9]、聚类[10-13]等方法提取端元,通过筛掉奇异值再合并成端元束。左成欢[14]采用PPI[15]提取并经过超像素分析保留的端元集,并根据植被指数将端元分类,通过聚类方法得到每类地物的端元束。陈立伟等[16]采用均值漂移算法完成聚类并提取端元束。上述方法依赖分块操作或预分类的结果,对于没有纯像元的高光谱影像容易提取出错误的端元。在集群智能算法方面,文献[17-18]提出了IQPSO和MODPSO。IQPSO通过极端重构误差判断所提取的端元是否是无效解,并通过端元函数判断是否结束迭代。该算法通过设定阈值控制算法迭代次数,容易出现迭代冗余,算法效率较低。MODPSO将端元提取作为多目标优化分析,采用0/1图像编码方式和速度及位置更新方式。该方法获取的端元束数量较少,无法准确表达地物的光谱信息。综上所述,采用集群智能算法效率低的主要原因在于:粒子编码、更新方式及迭代机制耗时较多。而提取端元数量少的原因在于:粒子迭代更新忽略了决策空间的分布特性,陷入了局部最优。因此,在端元束提取算法的设计上需要兼顾同类地物光谱的变化、提取精度、效率等,尽可能多地获取有效端元束。
本文为解决现有方法存在的问题,通过多目标多模态任务实现端元束提取。首先,对光谱图像进行一维标号编码,采用改进粒子群速度及位置更新方式更新粒子迭代信息。然后,引入环形拓扑结构改善粒子间的信息传递,提升信息搜索能力,并通过拥挤距离排序改善决策空间和目标空间的拥挤距离,最后,将端元束提取问题转换到多模态多目标的问题上,提高算法效率的同时实现端元束提取的有效性。
1 线性光谱混合模型与优化
光谱解混[19-20]依赖于场景混合模型,大尺度的光谱混合可认为是线性混合问题[21]。本文主要围绕线性混合模型进行混合像元问题的探究,并在此基础上提出基于多模态多目标优化的端元束提取方法。
1.1 线性光谱混合模型
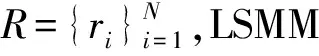
(1)
式中ej——端元
aij——端元ej在像元ri中的权重,即丰度
εj——误差项
q——端元数量
由于aij的物理意义是端元在像元中的面积比,需满足“非负约束”以及“和为1约束”两个条件,即
aij>0
(2)
(3)
本文将LSMM模型的求解方法建立在基于纯像元假设的基础上,所提取的端元均源于高光谱影像R中的像元,通过搜索像元提取端元束。
1.2 多模态多目标优化
多目标优化问题定义为
(4)
式中o——待优化的目标数
x——d维决策变量
gz(x)——不等式约束
hj(x)——等式约束
k——不等式约束数量
s——等式约束数量
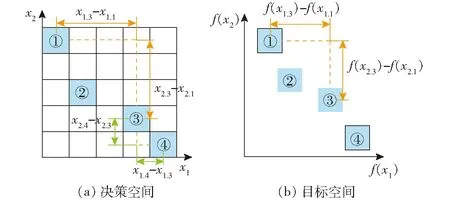
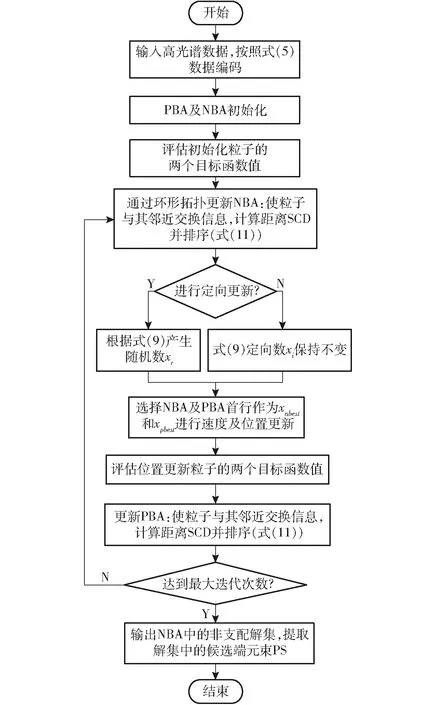
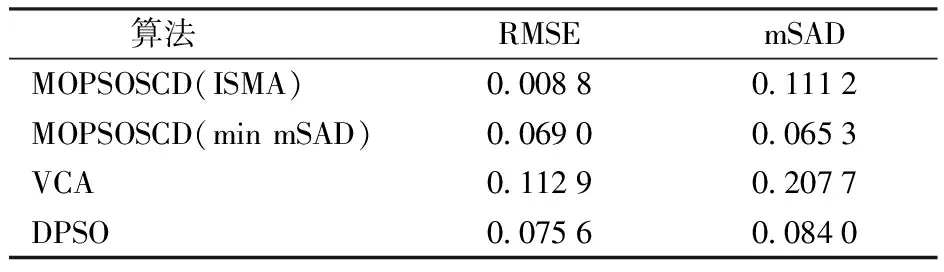
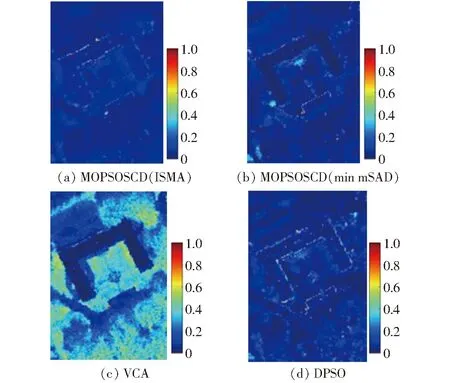
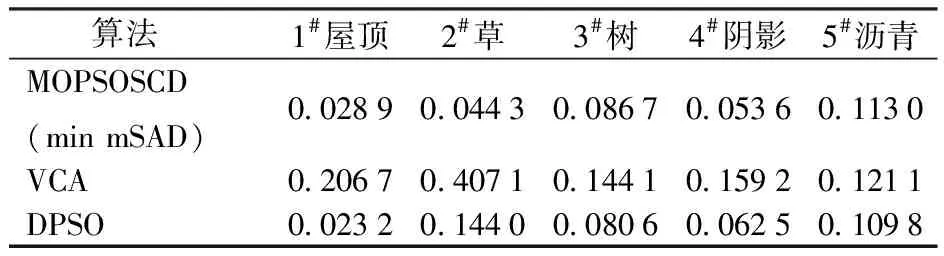
决策变量需满足k个不等式约束gz(x)≤0,z=1,2,…,k,以及s个等式约束hj(x)=0,j=1,2,…,s。同时满足以上约束的两个空间分别为决策空间R(d)和决策空间映射出的目标空间R(o)。因此,在给定一个包含o个目标的优化问题时,当且仅∀fi(x1)≤fi(x2)∧∃fj(x1) 多模态多目标问题如图1所示,以待优化目标数o=2为例,点p1、p2对应的目标空间值都为f(x1)。多模态特点就在于解的形态是多样的,即在保证目标值最优的情况下可以找到不同的解。一方面可以更深入地了解该组合解的分布规律。另一方面,混合像元分解的目的在于求解出像元所含地物的光谱特征。而光谱变异性导致了同类地物在不同像元的光谱特征存在的差异。该情况下,没有绝对的最优解,决策空间提供多组解应对光谱特征的变化。 图1 多模态多目标问题示意图 通常,多模态多目标问题满足以下条件之一[23]:①至少有一个局部帕累托最优解。②至少有两个等效全局帕累托最优解,它们对应PF上同一点。对满足多模态多目标条件的高光谱影像进行端元束提取。 高光谱影像特征复杂,虽然集群智能算法能够实现端元束提取[17-18],但在寻优过程中未考虑到PS的分布,无法在广泛空间中寻优,导致获得有效端元数量较少。本文采用多模态多目标解决端元束提取问题主要关注两方面:①提高算法搜索能力,搜寻较多的帕累托最优解。②尽量保留目标空间距离较小而决策空间较大的解,同时保证决策空间和目标空间的多样性。 集群智能算法通过简单信息处理单元之间的信息交流产生一种解决问题的能力。通常包括种群编码及初始化、种群进化与更新、筛选下一代种群、循环变异直至满足终止条件4个主要步骤。粒子群优化算法(Particle swarm optimization, PSO)是集群智能算法的主要代表,仿照鸟群觅食进行算法设计,主要用于解决可行解空间连续的单目标优化问题。本文所探究的可行解空间是离散集合,且从多模态多目标角度提取端元束。因此,在采用PSO算法的基础上,均需要对粒子编码、速度与位置更新、决策空间与目标空间排序及目标函数方面进行调整及优化,提出一种多模态多目标优化的端元束提取方法(Multi-modal and multi-objective particle swarm optimization by special crowding distance, MOPSOSCD)。 对于大小为n×h×l的高光谱影像R,以图像从左到右、从上至下对像元标号,并对图像中的像素位置编码,像素点编号集合Z为 Z={z1,z2,…,zn×h} (5) 通过该编码方式,粒子的位置编码还原至影像中形成多组端元解。其中,进行种群进化时某一组可行解为 X={x1,x2,…,xq} (xi∈Z) (6) 式中X——粒子像元对应的标号组成的序列 每个X对应一组端元E=[e1e2…eq]T。粒子初始化时,按照设定的粒子数随机生成矩阵E进行速度与位置更新及迭代。 PSO算法通过迭代寻优,在每次迭代中通过跟踪个体最优xpbest和全局最优xgbest更新自身的速度和位置,粒子i第t+1代的速度和位置更新分别为 vi(t+1)=ωvi(t)+c1(xpbest,i(t)-xi(t))+ c2(xgbest,i(t)-xi(t)) (7) xi(t+1)=xi(t)+vi(t+1) (8) 式中vi(t+1)——粒子的更新速度 ω——惯性系数 c1、c2——学习因子 xi(t+1)——粒子的更新位置 本文的高光谱影像编码方式导致粒子为离散形式更新,需在每个粒子位置更新完成后对该值取整。同时,为了保证所更新的粒子位置位于寻优范围内,将式(8)改进为 (9) 式中 ceil()——取整函数 xr(t+1)——区间Z内的随机数 在多模态多目标优化中,粒子的选择极为关键,本文采用MO_Ring_PSO_SCD[24]方法进行粒子信息传递和特殊拥挤距离计算。针对信息传递,设置个体最优xpbest的存档PBA和邻域最优xnbest的存档NBA,在邻域最优和子代最优选择中采用环形拓扑更新方式,其更新规则为:对于初始化或者已经进行迭代更新的粒子群,当粒子j为1~P(P表示粒子数量)时,拓扑更新表现为粒子j仅与j-1和j+1粒子进行信息交互,当j=1时,拓扑更新表现为粒子j与P和第2个粒子进行信息交互,当j=P时,粒子j与第1个和P-1粒子进行信息交互,以此形成闭环拓扑结构信息传递。因此,将式(7)更新方法调整为 vi(t+1)=ωvi(t)+c1(xpbest,i(t)-xi(t))+ c2(xnbest,i(t)-xi(t)) (10) 对于多模态多目标优化算法,需同时考虑决策空间和目标空间中个体的优劣问题。特殊拥挤距离Si可表示为 (11) 式中Ci,x——第i个粒子的决策距离 Cavg,x——决策距离平均值 Ci,f(x)——第i个粒子的目标空间距离 Cavg,f(x)——目标空间距离平均值 决策空间在空间分布上为离散问题,其数值范围为区间Z内的正整数。中间粒子的决策距离表示为 (12) 其中 d=q 式中d——决策空间维度 δ——决策空间加权项 通常为保证决策空间计算的有效性,令δ=1。如图2a所示,以二维决策空间计算为例,如获取粒子②在决策空间中的距离,则通过左右粒子①、③以及空间中最大最小值计算得 图2 决策空间与目标空间拥挤距离计算方法示意图 (13) 如果计算边界粒子的决策距离,边界粒子i=P时计算方法为 (14) 粒子④在决策空间中的距离可通过自身及临界粒子计算,计算式为 (15) 同理,边界粒子j=1时计算方法为 (16) 目标空间在空间分布上可认为是连续问题,由于目标函数值的区间不同,通常将目标空间值归一化后进行距离计算。计算中间粒子的目标空间距离方法与决策空间类似,即 (17) 如图2b所示,粒子②在决策空间中的距离同样通过左右粒子①、③以及空间中最大、最小值计算得到,计算方法为 (18) 计算目标空间的边界点与决策空间不同,本文解混问题为最小优化问题,当粒子某目标值最小时,将该方向的值设置为1,反之设置为0。例如:粒子④在目标空间中的距离为C4,f(x)=0+1=1。 (19) 基于多模态多目标优化的端元束提取方法流程如图3所示。结合上文所描述的MOPSOSCD方法,具体步骤为:①输入大小为n×h×l的高光谱数据R,按照数据从上至下,从左至右标号编码,进行粒子初始化并设置相关参数:定向选择概率pm、粒子数量P及迭代次数M。②采用目标函数评估初始化粒子的两个目标函数值。③通过环形拓扑结构更新NBA,使粒子与其邻近交换信息。④根据式(11)计算NBA的距离信息S:包含式(12)、(14)、(16)所计算的决策空间距离及式(17)所计算的目标空间距离,再按照距离信息S对NBA排序。⑤按照定向选择概率pm随机产生更新索引并判断PBA的首行元素是否在更新索引中:若是,按照式(9)生成随机数xr,执行步骤⑥;若否,xi保持不变,执行步骤⑥。⑥选择NBA及PBA首行作为xnbest和xpbest进行速度与位置更新。⑦评估位置更新粒子的两个目标函数值。⑧更新PBA:使粒子与其邻近交换信息。⑨根据式(11)计算PBA的距离信息SCD:包含决策空间距离、目标空间距离,再按照距离信息SCD对PBA排序。⑩判断是否达到收敛极限或达到最大迭代次数M;若是,执行步骤;若否,返回执行步骤④。输出NBA中的非支配解集,提取解集中的候选端元束,即为非支配解组成帕累托最优解集PS,并得到相应帕累托前沿PF。 图3 基于多模态多目标优化的端元束提取方法流程图 如图4a所示,采用MUUFL高光谱数据(https://github.com/GatorSense/MUUFLGulfport)进行本文算法验证[25-26]。MUUFL数据搭载高光谱仪的有人机飞行高度为1 066.8 m,空间分辨率为1 m×1 m,该影像共包括64个波段,覆盖波长443.9~967.2 nm,光谱分辨率为19.1 nm,本文选取其中图像尺寸为90像素×130像素的ROI区域进行试验验证[27]。如图4b、4c所示,ROI区域内含1#屋顶、2#草、3#树、4#阴影、5#沥青5种端元。 为验证本文算法的有效性,除了采用基于无约束最小二乘法(ucls)解丰度并反混后与原图的RMSE评价指标外,还采用光谱角距离(SAD)进行评价。光谱角表示两个光谱向量之间的光谱角信息,计算式为 (20) 式中b1、b2——光谱向量 将提取端元与实测光谱代入计算,两者相似程度越高,SAD越小,则说明端元提取效果越好。 为验证本文方法有效性,设置MOPSOSCD算法定向选择概率pm=0.2、粒子数量P=30、迭代次数M=400。不同算法在MUUFL数据提取端元效果如图5所示,对于 1#屋顶、2#草、3#树、4#阴影、5#沥青获取的端元数量分别为5、7、7、7、5。 本文方法基于纯像元假设进行端元束提取,像素标注结果如图6所示。算法考虑到光谱变异性,从多模态多目标的角度实现更大范围寻优。因地物重叠、分散造成的混合像元较多,MUUFL数据的环境相对复杂。通过算法寻优结果可发现,对于1#屋顶、2#草、3#树、4#阴影端元采用MOPSOSCD算法能够实现大区域内搜索,尽管图6中5#沥青分布较分散,MOPSOSCD算法的提取更倾向于寻优到5#沥青的纯像元信息。由于MOPSOSCD属于多目标算法,个别端元存在错分现象。总体来说算法在保证扩大搜索空间,避免陷入局部最优的效果较好。 图6 MOPSOSCD算法端元提取结果 多模态多目标问题面临确定最终解[23],对于MOPSOSCD算法提取的端元束,采用基于无约束最小丰度的ISMA[28]算法逐个像素提取最优端元组合,计算评价指标。同时,MOPSOSCD算法所提取端元束中每一组解都可以作为一组端元提取结果,将MOPSOSCD算法所得端元束中最小mSAD(min mSAD)的端元组合,用于计算评价指标。以VCA(顶点成分分析法)[29]和同样基于迭代方式进行端元提取的DPSO[30]作为对比方法,分别在MUUFL数据上进行对比试验。VCA算法以线性光谱混合模型的几何学描述为基础,通过反复寻找正交子空间并计算图像矩阵在正交子空间中的投影向量二范数并逐次提取端元。不同算法在MUUFL数据上的评价结果如表1所示。 表1 MUUFL数据精度对比结果 由表1可知,VCA、DPSO及MOPSOSCD 3种算法均能提取5种地物的端元信息。MOPSOSCD算法采用ISMA获取的最终解为每个像元分配了最优的端元组合,具有最优RMSE。由于MOPSOSCD算法提取的31条端元均参与了每个像元最优端元组合的求解,无法具体求解mSAD及5个端元对应的SAD,因此,31条端元的mSAD值为0.111 2。端元束中最小mSAD(min mSAD)所构成的端元组合的RMSE及mSAD分别为0.069 0和0.065 3,均优于VCA及DPSO。其中,RMSE指标如图7所示。 图7 MUUFL数据均方根误差 由图7a可知,MOPSOSCD算法所提取的端元束被充分分配至每个像素中,说明每个像素的RMSE达到了相对最优值,同时验证了该数据光谱变异性的存在及端元束提取的必要性。通过图7b可知,在采用最小mSAD(min mSAD)所构成的端元组合时,对1#屋顶、2#草、3#树、4#阴影4种端元提取的效果较好,而RMSE较高的区域主要分布在5#沥青端元上。从VCA和DPSO的均方根误差(图7c、7d)中可发现,VCA算法均方根误差较大,无法有效区分各端元信息。DPSO算法提取的屋顶边缘以及具有植被分布的像元具有较高的均方根误差,尤其对2#草与3#树混合部分端元提取效果较差。因此,本文算法相对其他方法在地物边缘或地物混合区域的端元提取效果较好。mSAD指标对应各端元的SAD值如表2所示。 表2 各端元的SAD值 通过表2可发现,MOPSOSCD算法所提取的端元束最小mSAD达到最优效果,尤其对2#草和4#阴影端元提取效果优于VCA及DPSO算法。在1#屋顶和3#树的SAD与DPSO算法接近。采用VCA提取的端元与真实光谱差异性较大,造成各端元SAD较大。 进一步的,本文对比了3种算法的运行时间。当采用参数组合pm=0.2、P=30、M=400进行迭代时,MOPSOSCD算法耗时32 741 s。相同参数组合的DPSO算法运行耗时80 123 s,VCA算法运行耗时3.47 s。对于经典的VCA算法来说,其优势在于,相对DPSO和MOPSOSCD 2种算法耗时较短。DPSO和MOPSOSCD 2种算法更加倾向于寻优效果和精度的提升。相较于DPSO,MOPSOSCD可以快速地提取更多可供决策的候选端元,构成端元束。 提出了一种基于多模态多目标优化的端元束提取方法。首先,将高光谱图像进行标号编码,并通过设定邻域最优存档NBA及个体最优存档PBA对粒子群速度及位置更新方式进行改进优化。同时,采用基于索引的环形拓扑结构实现不同邻域的个体进行信息交互,防止粒子随机更新,并改进决策空间拥挤距离,提高粒子在决策空间的多样性。最后,在MUUFL数据上验证算法有效性。当设置参数组合为pm=0.2、P=30、M=400时,MOPSOSCD算法的RMSE为0.008 8,提取的端元束的mSAD为0.111 2。该算法相较于其他算法在保证效率的同时获得更多有效端元束,且具有更高的精度。
2 基于改进离散粒子群的端元束提取
2.1 粒子编码
2.2 改进粒子速度与位置更新
2.3 环形拓扑结构与拥挤距离
2.4 目标函数
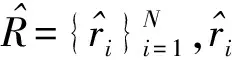
2.5 算法流程
3 试验结果与分析
3.1 试验数据
3.2 评价指标
3.3 试验及讨论

4 结束语
