基于低成本惯导和运动约束的农机高精度定位系统研究

袁洪良 杨浚宇 唐 睿 杜建伟

(1.同济大学电子与信息工程学院, 上海 201804; 2.中移(成都)产业研究院, 成都 610041)

0 引言

自主导航农机是实现智能农业的核心技术装备,可以全程参与耕、种、管、收环节的生产活动,达成提高作业效率、作业质量、土地利用率和降低劳动力成本等目标[1-5]。这些自主生产作业活动需要较高的定位精度支持,通常在厘米级。全球导航卫星系统(GNSS)[6-8]可以提供准确的绝对定位信息,但具有低频率和易受环境影响的缺点。相比之下,微机电惯性导航系统(MEMS-INS)可以在不受外部环境干扰的情况下稳定地提供相对定位信息[9-10],但具有误差累积的局限性。GNSS/INS组合导航系统[11-13]可以通过扩展卡尔曼滤波器(KF)有效地融合来自每个子系统的数据,提供稳定的高精度定位信息。因此,越来越多的GNSS/INS组合系统正在取代GNSS导航系统,成为农业机械自主导航系统的主要组成部分。然而,高性能的IMU成本非常高,影响自主导航农机推广,因此有必要研究基于低成本IMU的GNSS/INS组合导航系统,适应农业场景需求。

但是,GNSS/INS组合导航系统应用在农机上,存在一些技术问题。比如,大部分农机没有悬架系统,当农机作业时,必然存在较大的车体振动,由此导致GNSS测量精度下降,方差增大,估计误差增加[14],从而影响定位和控制效果。其次,农机在农田作业时,也有可能会遇到卫星信号遮挡、干扰或收星数不足等问题,导致GNSS短暂中断,GNSS/INS组合导航系统将退化为纯惯性导航系统[15-18],导航误差会随着时间的推移迅速增长,可能导致农机失控,造成经济损失。最后,GNSS/INS组合导航系统在低速或零速时存在航向角误差不可观测的问题[19-21],导致航向角随着时间发散。

许多研究中使用神经网络[22]或者增加外部传感器[23-24]来解决GNSS中断时定位误差发散的问题,但是对于农机,使用高算力的人工智能芯片或者增加外部传感器会增加系统的成本和复杂度,不利于在农业应用中大范围推广。

本文以东风DF1004-2型拖拉机为实验平台,设计BDS/INS组合导航系统。同时,为了解决BDS信号中断时的定位误差发散和组合导航系统中航向角误差累积问题,设计零速修正(ZUPT)和航向约束算法。该方法将在不增加其他外部传感器以及系统成本的基础上,解决当前农机组合导航系统中的固有问题,以利于系统在农业中应用推广。

1 BDS/INS组合导航系统设计与实现

1.1 硬件架构设计

硬件架构设计如图1所示,包括流动站和基准站。基准站接收来自北斗卫星的导航信号,并解析RTK校正数据,通过433 MHz无线电台发送到安装在农机上的流动站。流动站接收来自北斗卫星的导航信号,同时应用来自基准站的RTK数据解算出高精度定位信息。自动驾驶控制器完成INS的机械编排,并通过扩展卡尔曼滤波(EKF)得出组合定位结果。

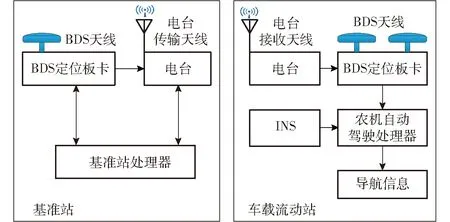
图1 组合导航系统架构

本研究MEMS-IMU模块为IMU383ZA-400,北斗定位模块为UB482,如图2所示。

图2 MEMS-IMU和GNSS模块

1.2 组合算法设计

BDS/INS组合导航系统算法分为两部分:INS机械编排和基于EKF的组合导航算法。

导航坐标系定义为北东地坐标系,用n表示;农机坐标系用b表示;地心地固坐标系用e表示;惯性坐标系用i表示。机械编排在n系下进行,具体过程如图3所示。MEMS-IMU输出的比力和角速度经过误差补偿后,通过坐标转换矩阵,转化到n系下。其中,比力经过比力方程计算后可以得到对应的加速度,继续对其进行积分,即可获得由INS推算出的位置和速度信息。角速度则通过姿态计算微分方程对坐标转换矩阵进行更新,从而根据其与姿态角之间的对应关系得出姿态信息。

图3 机械编排

对应的微分方程为

(1)

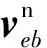
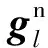
h——农机高度

vD——农机垂向速度

选取组合导航系统的15维状态向量为

x=[ΔLΔλΔhδvNδvEδvDδφδθδφ

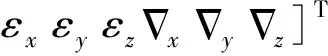
(2)

式中 ΔL、Δλ、Δh——纬度、经度、高度误差

δvN、δvE、δvD——三轴速度误差

δθ、δφ、δφ——三轴姿态误差

εx、εy、εz——三轴陀螺仪零偏

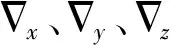
基于INS的误差模型[25]在n系下可以表示为

(3)

式中 δrn、δvn、Ψ——位置、速度和姿态误差

δgn——重力加速度误差

δfb——加速度计测量的比力误差

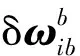
将陀螺仪和加速度计误差建模为一阶马尔可夫过程,因此,离散EKF系统模型可以表示为

xk=Φk,k-1xk-1+Wk-1

(4)

其中

(5)

Φrv=[I3×3Δt]3×3

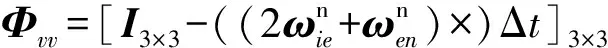
Φva=[(fn×)Δt]3×3

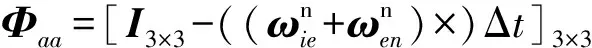
Φbgbg=diag(e-Δt/Tgb,e-Δt/Tgb,e-Δt/Tgb)

Φbaba=diag(e-Δt/Tab,e-Δt/Tab,e-Δt/Tab)

式中Φk,k-1——状态转移矩阵

Wk-1——过程噪声

I3×3——3×3单位矩阵

Δt——每个历元的时间间隔

R——平均曲率半径

Tgb、Tab——陀螺仪和加速度计的相关时间

系统测量方程可以表示为

zk=Hxk+V

(6)

其中

式中zk、H——系统观测量和观测矩阵

V——测量噪声向量

EKF的更新方程为

(7)

式中K——卡尔曼滤波增益

Q——测量噪声协方差矩阵

P——估计误差协方差矩阵

P初始值由实地测试给出,即

P0=diag(0.52,0.52,0.52,0.52,0.52,0.52,0.0872,

0.0872,0.1742,0.000 242,0.000 242,0.000 242,

0.012,0.012,0.012)

因此,整个BDS/INS组合导航系统框图如图4所示。通过INS机械编排获得三轴位置和速度信息之后,将INS与BDS定位结果间的差值作为位置误差、速度误差的观测值,利用EKF估计定位误差,反馈校正定位结果。

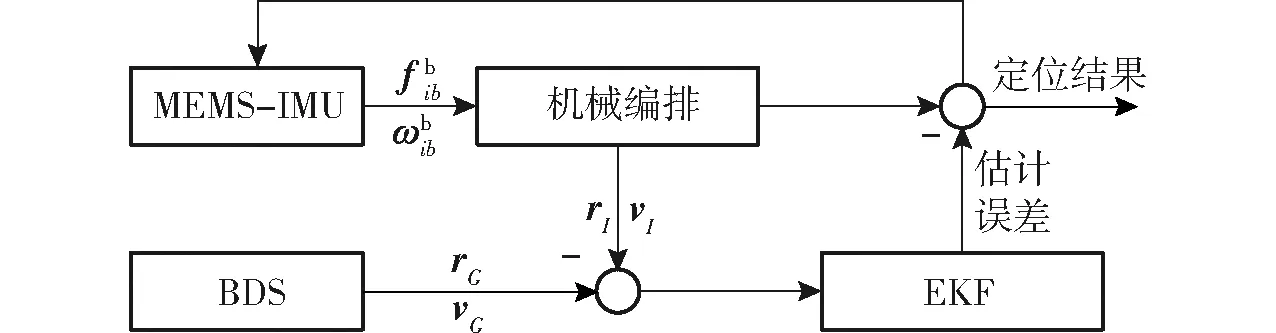
图4 BDS/INS组合导航系统框图

1.3 零速修正和航向约束算法设计

(1)零速判断

对于ZUPT和航向约束两种算法,判断农机是否处于静止状态是十分重要的问题。这里定义一个新的变量δp为

(8)

式中 |δp|——相邻两个历元之间的位置差值

rlat、rlon、rh——BDS给出的当前时刻的纬度、经度和高度

r′lat、r′lon、r′h——BDS给出的上一时刻的纬度、经度和高度

Rm、Rn——子午圈和卯酉圈的曲率半径

当|δp|小于设置的阈值,则判定农机处于静止状态并使用ZUPT和航向约束算法。

(2)ZUPT算法设计

当农机静止时,其3个方向的实际速度为零。然而,来自GNSS的速度信息存在随机误差。ZUPT通过将包含随机误差的速度信息替换为零,提高了速度观测值的精度,从而提高了组合导航系统的定位精度。此外,当GNSS中断时,ZUPT不会受到影响,可用于在此期间保持定位精度。

基于这一原理,本文针对BDS信号可用和中断两种情况,设计了ZUPT算法,并通过改变式(6)中的速度误差观测量来实现。

首先,当BDS信号可用时,将BDS给出的速度信息替换为0。因此,观测量和观测方程可以改写为

(9)

其次,当BDS中断时,组合导航系统会缺失来自BDS的位置、速度信息。因此,观测量中没有位置误差,但ZUPT可以提供速度误差观测值,此时系统的观测量和观测方程可以改写为

(10)

(3)航向角误差不可观测的原因分析

低成本MEMS-IMU,通常存在明显的噪声。此外,农机作业时也会产生车体振动,从而影响IMU的输出。与这些外部干扰相比,地球的自转速度和重力加速度误差很小。因此,在IMU的输出中可以忽略不计,式(3)中的INS误差方程可以简化为

(11)

式中 δθ、δφ、δφ——横滚角、俯仰角和航向角误差

由式(11)可以得出,航向角误差只能通过前向和右向的比力来观测。然而,农机通常处于静止或匀速工作状态,此时农机前向和右向的比力均为0,因此航向角误差不可观测。这导致了航向角会随时间发散。与之相比,横滚角和俯仰角可以通过垂向比力来观测。

(4)航向约束算法设计

在本文所设计的系统中,BDS选用双天线结构(DA),因此测量出的偏航角具有较高的精度,当BDS信号可用时,将BDS信息中给出的偏航角与INS推算出的航向角之间的差值作为航向角误差的观测值,可以有效地抑制航向角误差的累积。因此,将式(9)中的测量方程扩展一维,系统的测量方程可以改写为

(12)

其中

E=[0 0 1]

式中φI——INS推算出的航向角

φB——BDS信息给出的偏航角

然而,式(12)中利用DA的方法需要确保BDS信号的可用。在系统中断导致信号不可用时,该方法便失去了作用。因此,有必要针对此种情况设计另外的航向约束算法。

按照式(11)的处理方式,式(3)中的姿态角误差方程可以改写为

(13)

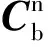
(14)

式中cφ、cθ、cφ、sφ、sθ和sφ表示cosφ、cosθ、cosφ、sinφ、sinθ和sinφ。

将式(14)代入式(13)中,则航向角误差方程可以表示为

(15)

由式(15)可以得出,当农机静止在农田中时,横滚角和俯仰角接近于零,因此航向角误差主要来源为陀螺仪z轴测量的角速度误差。因此,可通过减小z轴角速度误差来抑制航向角误差的发散。

当农机处于静止状态时,z轴角速度的真实值为0,因此可以将0与陀螺仪z轴角速度的差值作为误差观测值。基于此,设计了零角速度修正算法(ZARU),与DA组合使用。

同样将式(10)中的测量方程扩展一维,可以得到此时的系统测量方程为

(16)

综上所述,整个系统的示意图如图5和图6所示。当BDS信号可用时,由ZUPT和DA辅助的BDS/INS组合导航系统的框图如图5所示。INS推算出的航向角与BDS信息给出的航向角之间的差值作为航向角误差的观测量增加到系统中。

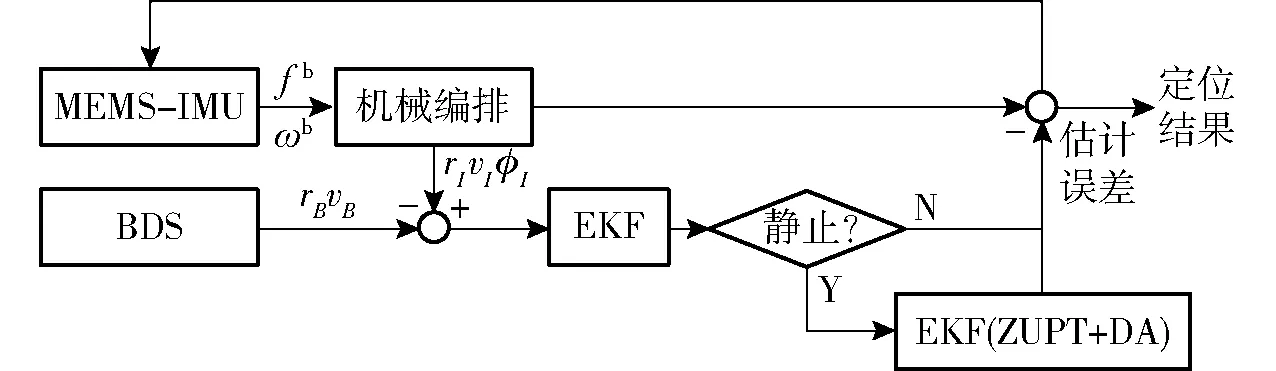
图5 BDS/INS/ZUPT/DA组合导航系统框图

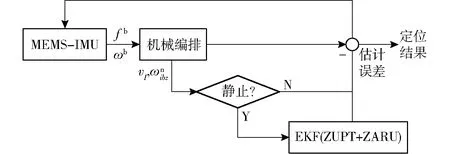
图6 BDS/INS/ZUPT/ZARU组合导航系统框图

当BDS中断时,由ZUPT和ZARU辅助的BDS/INS组合导航系统框图如图6所示。与BDS信号可用时不同,这里没有位置误差和航向角误差的观测值,但增加了z轴角速度误差作为观测量。

2 实验

实验平台采用东风DF1004-2型拖拉机搭建。使用第1节中的架构,设计并制作了基准站和流动站的印刷电路板(PCB)。基准站放置在没有遮蔽的开放区域,以提供连续的RTK数据。流动站安装在拖拉机的驾驶舱内。BDS双天线水平放置在车顶上,基线长度为1.2 m。电台天线安装在左后轮挡泥板上。实验平台构成和测试现场如图7所示。

本文提出的算法在农机实验平台上进行测试。测试分为两部分:测试A是验证当BDS信号可用时,ZUPT和DA航向约束对定位精度的改善;测试B是验证当BDS信号中断时ZUPT和ZARU航向约束对定位精度的改善。两组测试实验中,在检测到农机静止后,ZUPT和航向约束每隔0.5 s应用一次。

2.1 测试A

当BDS信号可用时,将农机静止于稻田中,通过BDS/INS、BDS/INS/ZUPT以及BDS/INS/ZUPT/DA获得的定位误差如图8～10所示。表1中给出了定位误差的最大值和均方根误差。

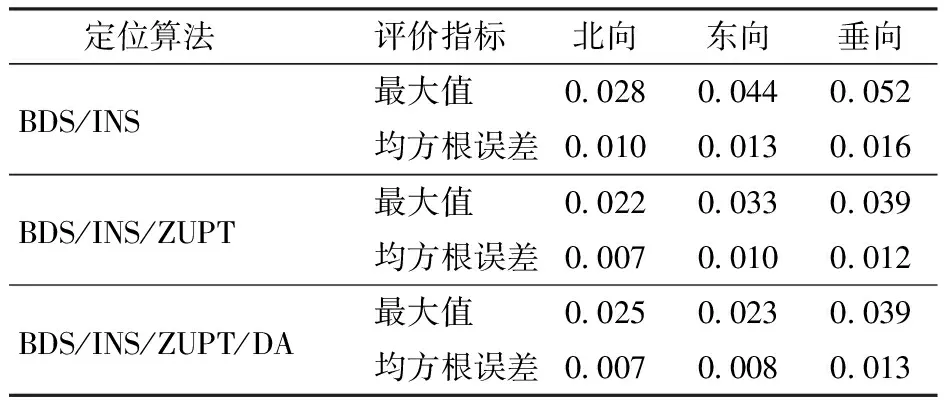
表1 BDS信号正常时速度误差的最大值和均方根误差

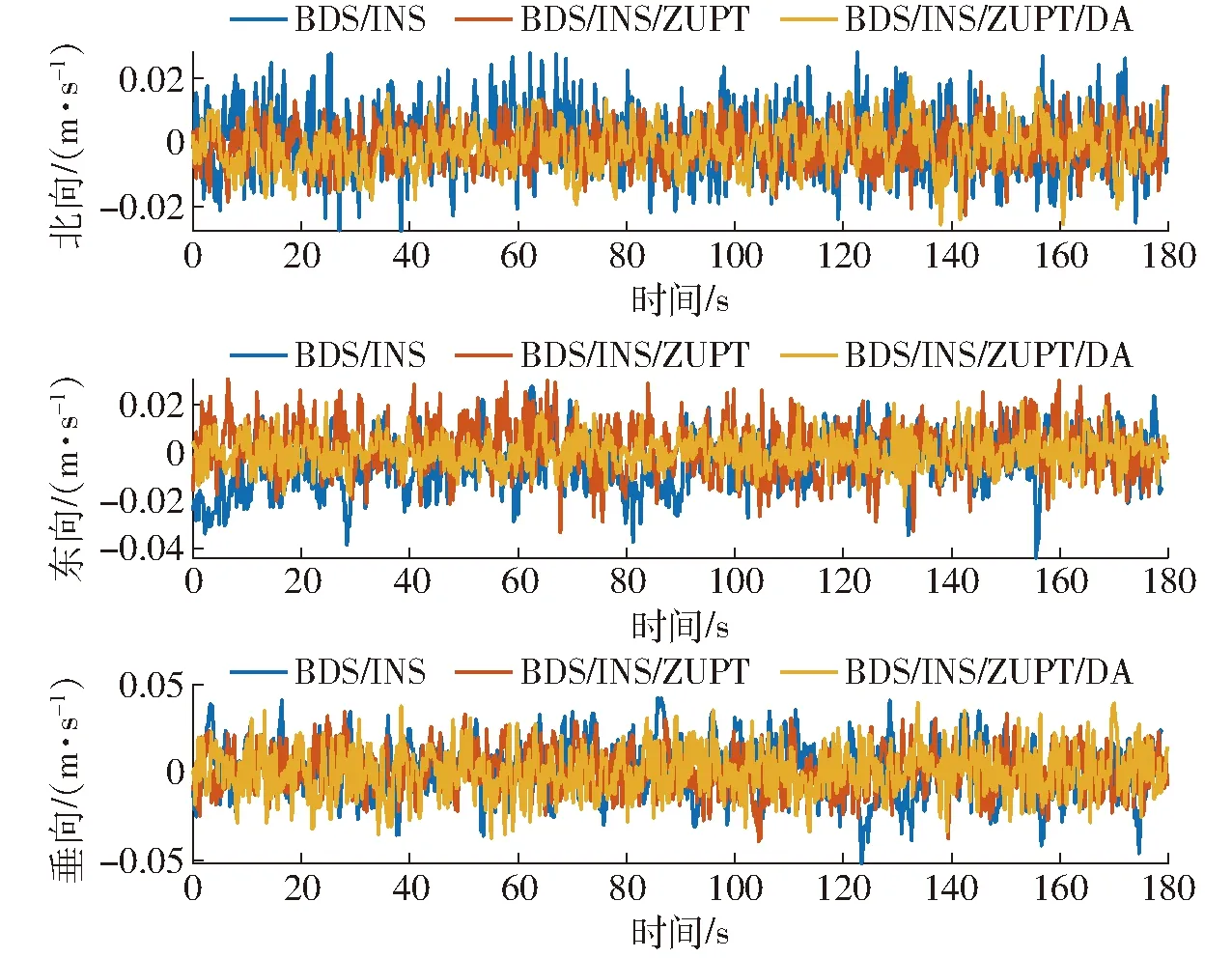
图8 BDS可用时的速度误差

如图8和表1所示,BDS/INS组合导航系统在3个方向的最大速度误差分别为0.028、0.044、0.052 m/s,相应的均方根误差分别为0.010、0.013、0.016 m/s。应用ZUPT后,3个方向上的最大速度误差分别降至0.022、0.033、0.039 m/s,相应的均方根误差也变得更小,分别为0.007、0.010、0.012 m/s。准确度分别提高30%、23%和25%。而BDS/INS/ZUPT/DA与BDS/INS/ZUPT相比,其对速度误差的影响较小。

如图9和表2所示,对于BDS/INS,北向和东向的最大位置误差分别为0.028 m和0.015 m,最大垂向误差为0.048 m。3个方向的均方根误差分别为0.009、0.005、0.017 m。应用ZUPT之后,北向和东向的误差分别减小到0.012 m和0.010 m。垂直方向的最大误差减小到0.017 m。3个方向的均方根误差分别为0.005、0.003、0.006 m,精度分别提高44%、40%和65%。与速度误差的改善结果相同,增加DA不会显著影响位置误差。

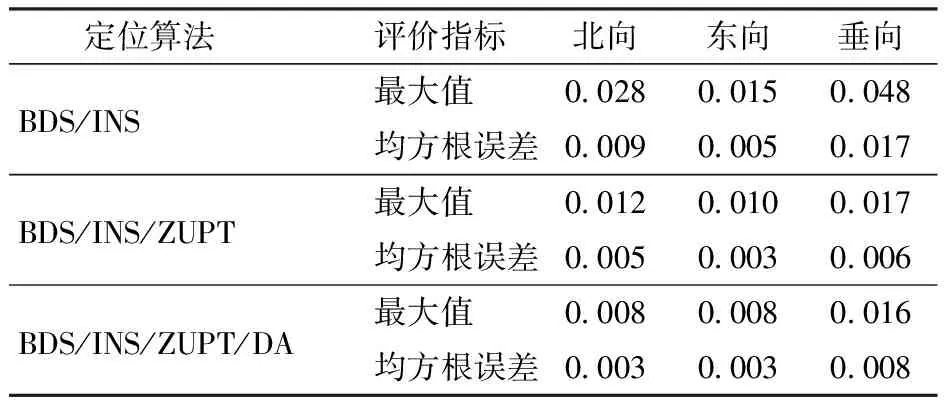
表2 BDS信号正常时位置误差的最大值和均方根误差

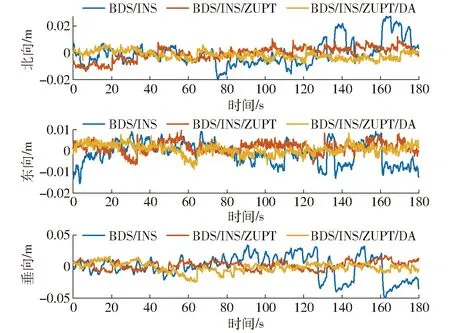
图9 BDS可用时位置误差

如图10和表3所示,BDS/INS组合导航系统可以提供准确的水平姿态角信息。最大横滚角误差为0.265°,对应的均方根误差为0.069°;最大俯仰角误差为0.078°,相应的均方根误差为0.030°,航向角误差在180s内累积到13.582°。应用ZUPT后,横滚角和俯仰角的精度得到了提高。其中,横滚角的最大误差减小到0.200°,均方根误差减小到0.034°,精度提高51%。俯仰角的最大误差减小到0.016°,均方根误差减小到0.020°,精度提高33%。此外,增加使用ZUPT后,对航向角精度的改善不大。应用DA之后,BDS/INS/ZUPT/DA将横滚角的最大误差减小到0.130°,均方根误差减小到0.024°,精度提高29%。最大俯仰角误差减小到0.010°,均方根误差减小到0.017°,精度提高15%。航向角最大误差为0.012°,均方根误差为0.041°,有效抑制了航向角误差的累积,解决了在静止时航向角误差发散的问题。

表3 BDS可用时姿态误差的最大值和均方根误差

图10 BDS可用时姿态误差

综上所述,BDS/INS组合导航系统可以稳定地为农机的自主驾驶提供定位信息。ZUPT通过提高速度误差观测值的准确性提高了速度的精度,减小了速度误差。同时,由于位置是通过速度积分获得的,ZUPT改善了速度误差,因此位置误差也会随之改善。然而,由于航向角误差不可观测,而ZUPT并不能提高航向角误差的可观测度,因此不能抑制航向角误差的发散。DA通过提供BDS的偏航角提高了航向角误差的可观测性,从而抑制了组合导航系统中航向角的发散。同时,由于姿态误差之间的耦合,横滚角和俯仰角的精度也得到了提高。

2.2 测试B

在本节的测试中,农机仍静止在稻田中。BDS/INS组合导航系统正常运行2 s后,人为地屏蔽BDS信号60 s,以模拟BDS信号不可用的情况。通过BDS/INS、BDS/INS/ZUPT和BDS/INS/ZUPT/ZARU获得的速度误差、位置误差和姿态误差如图11～13所示(图中未完全展示)。BDS信号中断的时刻在图中用黑色箭头标记。速度误差、位置误差和姿态误差的最大值和均方根误差见表4～6。

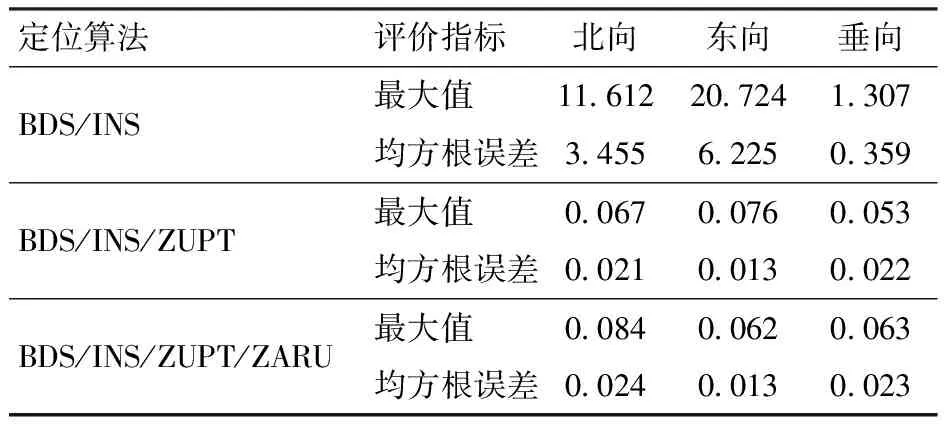
表4 BDS不可用时速度误差的最大值和均方根误差

图11 BDS不可用时速度误差

如图11和表4所示,在BDS中断的60 s内,速度误差迅速发散,3个方向的最大误差分别为11.612、20.724、1.307 m/s。相应的均方根误差为3.455、6.225、0.359 m/s,在实际生产中,这样的定位结果显然是不可用的。应用ZUPT后,速度误差不再发散,3个方向上的误差保持了与BDS信号可用时类似的精度,最大误差分别为0.067、0.076、0.053 m/s。相应的均方根误差分别降低到0.021、0.013、0.022 m/s,精度分别提高99%、99%和94%。在此基础上,进一步增加ZARU对速度没有进一步的改善。

如图12和表5所示,在BDS中断期间,位置误差随时间迅速发散,最大误差分别为195.834、332.672、21.741 m。相应的均方根误差分别为56.639、95.574、6.205 m。应用ZUPT后,位置误差的发散问题得到解决。3个方向的位置误差在0.06 m以内,相应的均方根误差分别为0.014、0.018、0.018 m,3个方向精度均提高90%以上。结果表明,在没有BDS信号的情况下,ZUPT在农机中的应用显著地改善了位置精度。在ZUPT的基础上,进一步使用ZARU不会对位置误差产生显著影响。

表5 BDS不可用时位置误差的最大值和均方根误差

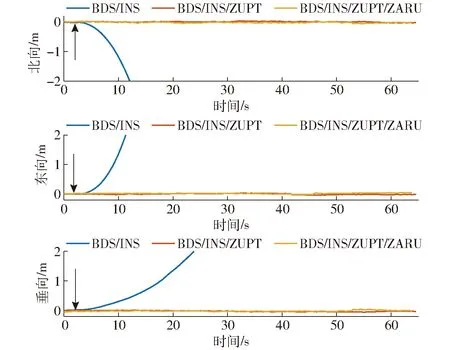
图12 BDS不可用时位置误差

如图13和表6所示,当BDS中断时,姿态误差逐渐发散。3个姿态角误差的最大值分别为4.972°、1.365°和4.685°,相应的均方根误差分别为1.491°、0.487°和1.429°。应用ZUPT后,横滚角和俯仰角的精度显著提高。两个姿态角的误差均在0.5°以内,均方根误差分别降低到0.103°和0.083°,精度分别提高93%和83%。然而,航向角误差的改善并不明显,最大误差和均方根误差分别为4.056°和1.209°,误差发散的问题仍然存在。继续增加提出的ZARU算法,最大误差减小到1.932°,均方根误差减小到0.629°,对于航向角误差的精度具有显著的改善,准确度提高48%。同时,保持了横滚角和俯仰角的精度。

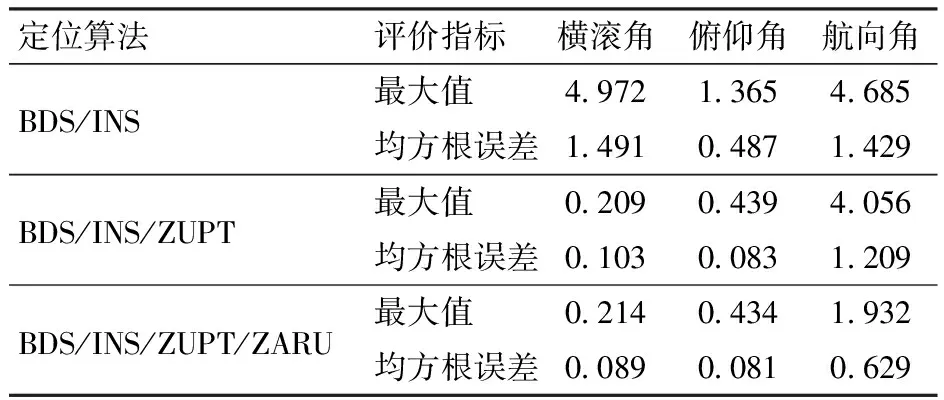
表6 BDS不可用时姿态误差的最大值和均方根误差

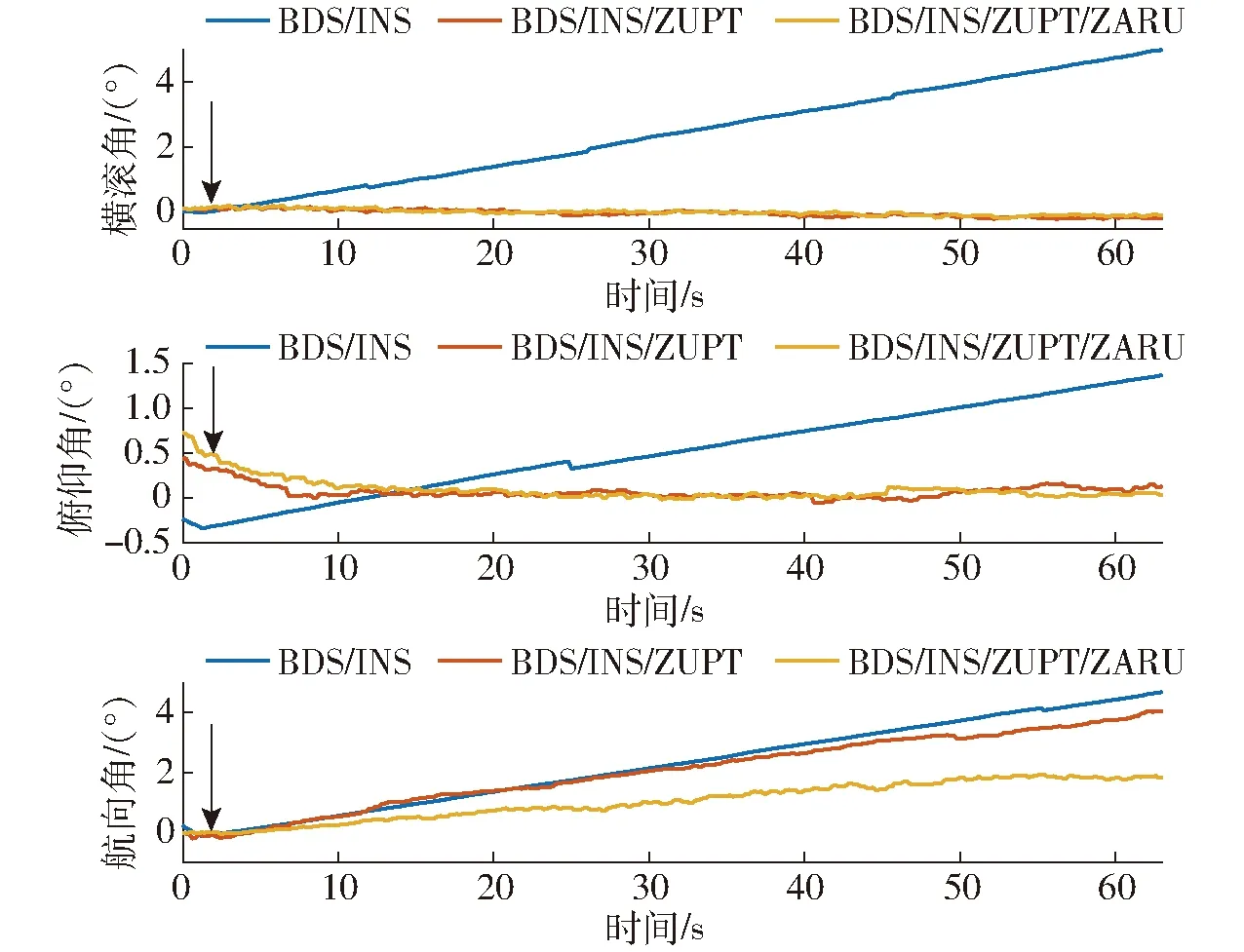
图13 BDS不可用时姿态误差

通过对实验结果的分析,可以得出BDS/INS组合导航系统在BDS中断期间退化为纯INS,速度误差、位置误差和姿态误差均逐渐发散的结论。ZUPT可以通过提供速度观测值来抑制速度误差的发散。此外,虽然没有位置误差观测值,但位置是通过速度积分获得的,因此应用ZUPT之后,位置误差的发散也可以得到解决。故而可以得出,ZUPT在复杂的农业生产环境中应用于农机可以达到令人满意的精度,这表明本文设计的组合导航系统和ZUPT算法具有良好的稳定性,能够满足农业生产的需要。然而,与BDS信号可用时相比,由于缺少位置观测值,精度略有降低。同时,ZUPT能够提高横滚角和俯仰角的精度,但是因为ZUPT不能够提高航向角误差的可观测度,因而不能提高航向角精度。继续增加ZARU,航向角误差明显改善。

3 结束语

采用低成本MEMS-IMU设计了BDS/INS组合导航系统,并在东风DF1004-2型拖拉机上进行了测试和验证。针对BDS信号中断期间定位误差发散以及组合导航系统中航向角误差不可观测的问题,设计了ZUPT和DA与ZARU结合的航向约束算法。现场实验表明,所提出的方法是有效的,BDS/INS组合导航系统可以为农业生产提供准确的定位信息。当BDS可用时,ZUPT可以将位置、速度和水平姿态的精度分别提高20%、40%和15%以上,使用DA的航向约束可以将航向角精度提高90%以上;BDS中断时,ZUPT可以将位置、速度的精度提高90%以上,水平姿态的精度提高80%以上,使用ZARU的航向约束可以将航向角精度提高40%以上。此外,所提出的方法不需要增加额外的传感器,降低了农机导航系统的成本,有利于该系统推广。