辩经形式语义学
2023-07-30许春梅
许春梅
一、背景
古印度因明,特别是其新因明,自8世纪开始传入西藏,并在传播发展中逐渐本土化,形成了独具特色的藏传因明。其中,名闻遐迩的当属辩经。11世纪,俄洛丹协绕以桑普寺为中心,建立了辩经院,革新论式,规范学风,通过辩难、讨论,进一步强化了因明学注重逻辑思维训练的特质,开启了西藏新因明时代。12世纪,恰巴·却吉桑格的《量论摄义祛蔽论》问世,西藏开始流行以恰巴·却吉桑格为代表的摄类辩论学,藏族学者纷纷推崇“应成”推论式辩论。13世纪,萨迦班智达贡噶坚赞撰写了西藏第一部因明学著作《量理藏论》,将认识论和逻辑推理有机地联系起来,从客观存在到感觉思维,再归纳出思维形式与规律,从而使量学思想自成体系,使西藏因明学在内容上更加完整和系统化。15世纪,格鲁派宗喀巴撰写的《因明七论除暗论》,将因明论式作为掌握、善巧运用佛学教理的重要方法,并始终贯穿到佛学理论的践行之中。在宗喀巴及其亲传弟子贾曹杰和克珠杰等的推动下,因明学的研习与传承得到前所未有的发展,深刻影响到藏传因明的发展,例如各大寺院都将《释量论》作为五部经论之首,格西(博士)学位的获取必须通过辩经。正是由于藏传辩经不仅在开发智力和研学佛学理论上有特殊优势,而且在理论建构、学说传播等方面亦起着重要作用,所以它在藏族传统文化中享有“开启智慧的钥匙”、“断除迷惑的利器”等美誉。
目前,我国因明界对藏传辩经的主要研究力量是藏语学者,汉语学者鲜有涉猎。在研究方法上,也主要是进行文献整理、(1)贡保扎西:《藏传因明学研究历史与现状综述》,《西南民族大学学报》2008年第6期,第41—43页。田野调查(2)次旺南木加:《承继与超越:藏传因明教育结构体系诠释》,《世界宗教文化》2021年第5期,第138—145页。等,运用形式化方法研究辩经的学者很少。2018年,笔者在《藏传辩经原则的形式化》中提出,(3)许春梅:《藏传辩经原则的形式化》,《世界宗教文化》2018年第6期,第118页。运用形式化方法对藏传辩经中辩论者如何问、立论者如何答以及如何构建一系列使辩论者必赢的应成论式等原则进行刻画,同时认为辩经本质上是剔除不一致、不自洽信念(或观念),是破邪立正的有效途径,具有普适性,其使用不仅仅局限于宗教学领域,从而为辩经研究提供了一个新的研究方法和视角。2019年,汪楠在《藏传因明辩经规则探析》中,(4)汪楠、杨武金:《藏传因明辩经规则探析》,《中国社会科学报》2019年10月8日,第5版。对立论者如何答方面给出了选择流程示意图,颇具新意。由此可见,形式化方法在研究、揭示辩经的形式、结构、本质等方面具有独特优势。(5)许春梅:《藏传辩经原则的形式化》,第118页。本文将继续在形式化方法上作新的尝试,希望在新因明思想指导下,通过引入形式语义学方法,为藏传辩经建立一套更为直观的模型语义解释。
二、以“红白”颜色之辩为例
“红白”颜色之辩是掌握藏传辩经技巧的一个经典训练案例。所谓“红白”颜色之辩,是指立、辩双方关于“所有颜色都是红色”这个论题而展开的一套有特殊格式和一定规则的辩论。立论者立了一个观点“若是显色,遍是红色故”,意思是说所有颜色都是红色。这是一个错误的观点,那么,辩论者要如何来证伪呢?通常只需找一个是显色,但又不是红色的反例即可。但是如果要让立论者心甘情愿地放弃其观点,这就不是一个反例就能解决的问题了。生活中经常遇到“刚强难化”者、“自以为是”者,即使将反例摆其面前,也是“八风不动”、死扛到底。因此,这就要求辩论时不仅逻辑推理上是必须成立的,同时每一步所给的论据也都是为立论者所接受的。藏传辩经有一套规则和方法来实现这样的要求,具体做法就是运用归谬法,即在承认立论者主张的前提下,依靠立论者自身认知,引导其一步步推出一对自相矛盾的结论,那么他就不得不放弃原来所持的主张了。“红白”颜色之辩,应先寻找一个是显色的,但不是红色的反例,比如白法螺,它是显色,但不是红色。按“三步走”展开辩论:第一步先立因,证明白法螺之显色是显色,由于已经暂时先承认立论者的观点“若是显色,都是红色”,所以可推出其是红色;第二步是立周遍,要证明“如果是白色,应非红色”,由于立论者在第一步的论辩中已经承认白法螺之显色是白色了,所以一旦周遍成立,则可逻辑地推出其不是红色。至此,已得出了一对矛盾,即“白法螺之显色既是红色,又不是红色”。因此,“白法螺之显色”就构成了对立论者的主张“若是显色,遍是红色”的反驳。第三步,就是立论者心悦诚服,主动放弃其原先主张。否则,如果坚持原主张“若是显色,遍是红色”,则必陷入自相矛盾之中,得出“白法螺之显色是红色又不是红色”这一自相矛盾的结论。下面是辩、立论者双方就“红白”颜色之辩的具体对扬过程:(6)许春梅:《藏传辩经原则的形式化》,第115—116页。(见表1)
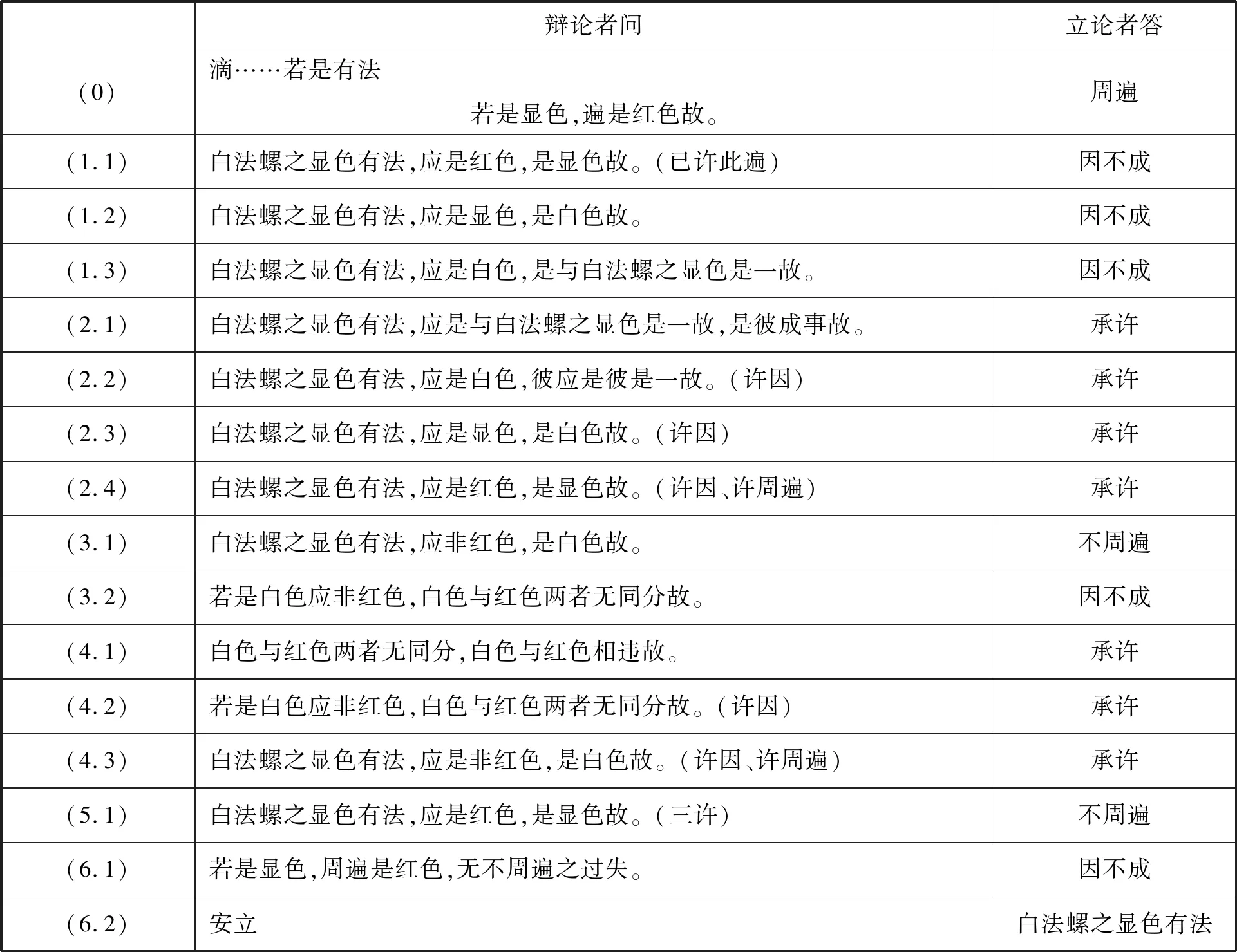
表1:“红白”颜色之辩对扬过程
由上述这个经典案例,不难发现藏传辩经的一些基本特点和要求。
首先,一个完整辩经的主要参与者是由立论者和辩论者组成。双方所承担的角色和功能不同。辩经起于立论者立一个观点,这个观点引起争议,于是立论者就要接受他人的问难,因此,立论者在整个辩论过程中是回答方,那些问难者即是辩论者。
其次,辩论者如何问,以及立论者如何答,都必须遵循一定的规则和要求。凡问必以应成式来问。所谓应成式,就是形如“______有法,应是______,是______故”的语句形式。这种语句形式由三部分组成,即有法、所立法和因,且这三部分需明确分开。例如,在“馒头有法,应是吃的,是马故”这一应成式中,“馒头”是有法,“是吃的”是所立法,“是马故”是因。有法与所立法共同构成了宗或主张,该例的主张是“馒头应是吃的”。由此可见,应成式其实就是新因明论式中的“宗—因”式的变形。对于辩论者所给出的应成式,立论者只能从五种基本的回答中选择其一来作答。它们分别是:何故、承许、因不成、不周遍和周遍相违。若辩论者只提出宗而未给出因时,如果同意该宗,就可回答“承许”。反之,如果不同意,就回答“何故”,进而要求辩论者给出理由。如果认为所给的理由不成立,则回答“因不成”。如果认为所给的理由太大,超出所立法,则回答“不周遍”。如果认为所给的理由与所立法毫无相关,则回答“周遍相违”。为更直观理解,下表再举例以示说明(见表2):
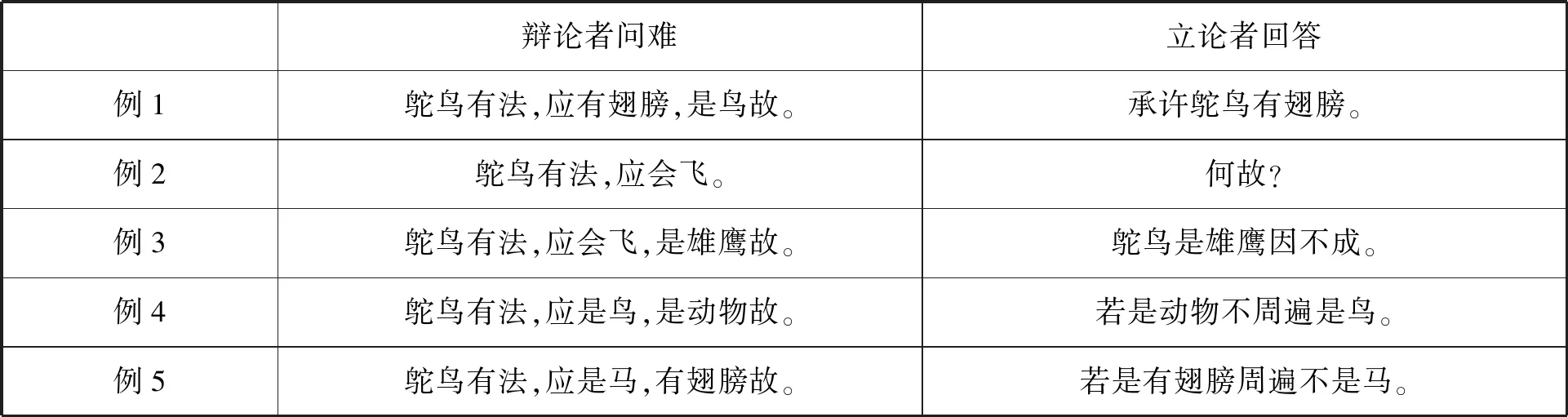
表2:应成式中立、辩双方问答范式表
第三,辩论中的推理要符合逻辑,即在每个应成式的构造中,必须保证有法是因,且因都是所立法。换句话说,应成式的三个部分在外延上必须具备这样的关系,即因包含有法,而所立法又包含因。如此一来,则有法就必然包含在所立法之中,立论者就必须承许“有法是所立法”或“有法有所立法”。(7)许春梅:《藏传辩经原则的形式化》,第118页。
第四,为了让立论者主动承认并放弃其原有主张,则辩论过程中只能依赖立论者的认知,即每一句应成式所给的因都必须为立论者所接受。那么,如何构造、寻找能为立论者接受的因呢?如上,“红白”颜色之辩的做法是不断收缩因的外延,使其后一个应成式的因被其上一个论式的因所包含,同时,又让上一个应成式中不成立的因作为下一个应成式的所立法来论证。这样,其结果如同多米诺骨牌效应一般,一旦立论者接受了某个因,就能迫使其接受一开始他最不愿意接受的因。(8)许春梅:《藏传辩经原则的形式化》,第118页。辩论者要使立论者接受(1.1)中的应成式,如果立论者不承许,由于已许周遍(0)“若是显色,遍是红色故”,所以他只能回答“白法螺之显色是显色,因不成”。辩论者又立(1.2)中的应成式,将(1.1)中不成的因当成所立法来论证,同时再找一个外延上比上一个因要小的因“白法螺之显色是白色”作为该应成式的因。这样处理后,立论者如果还不承许,就只能回答“白法螺之显色是白色,因不成”。辩论者按如此方法去构造论式,直至立论者接受该因为止。从(1.1)至(1.3),因的外延一个比一个小,“显色”包含“白色”,“白色”包含“与白法螺之显色是一”等。直到选择“与白法螺之显色是一”这一因,此时立论者不得不接受,因为该因是同一律。在实际的辩论中,因序列的收缩不一定非得要收缩至逻辑律,只要收缩至立论者能接受就行。
第五,整个辩经过程包含了推理过程和寻找因的过程。具体地,从(1.1)至(1.3)部分是寻找可为对方接受的因的过程,从(2.1)至(2.4)部分则是根据所找的因进行推理的过程,它们共同完成了“白法螺之显色有法,应是红色,是显色故”的说明、推理过程。从(3.1)至(3.2)部分是寻找可为对方接受的因的过程,从(4.1)至(4.3)部分是根据所找的因进行推理的过程,它们共同完成了“白法螺之显色有法,应是非红色,是白色故”的说明、推理过程。
最后,藏传辩经的本质、特色在于它是剔除不一致、不自洽信念(或观念),(9)许春梅:《藏传辩经原则的形式化》,第120页。这是由其论辩的技巧决定的。由于论辩多采用归谬法,一旦在立论者的主张下能导出矛盾,就可安全地舍弃该主张。例如,在“红白”颜色之辩中,由立论者持的观点“显色都是红色”,导出了“白法螺的显色是红色”和“白法螺的显色不是红色”这一对矛盾,由于每一步推理都是建立在共许、逻辑推理之上的,如果接受“显色都是红色”,则必将使我们陷入自相矛盾之中,因此,不能接受该观点,应将其剔出我们的认知。
三、以新因明为基础的辩经形式语义学
我们将根据上述藏传辩经的特点和要求,结合新因明的思想,尝试给出一套辩经形式语义学。形式化的过程,首要的一步就是选择语言符号。从现存的佛经、论来看,《瑜伽师地论》卷15,本地分中闻所成地第十之三已深入研究宗支的内部结构,认为一个论题由两部分构成:一是自性部分;二是差别部分。(10)弥勒菩萨:《瑜伽师地论》卷15,载于玄奘译,《大正藏》第30册。这种观点为瑜伽行派所重视和传承。从弥勒、无著、世亲、陈那、法称等瑜伽行派的著作中皆能见到相似论述。探讨句子内部的部分性质及其部分间的关系,在新因明时代已经是很普遍的。为此,我们选择谓词符号在内的词项语言,主要探讨谓词间的关系及其直言语句间的推理。
(一)语言(L)
1.变元符号:x、y、z、……
2.谓词符号:Ρ、Q、S、……
3.词项联结词:A、E
5.辅助符号:(、)
值得注意的是,虽然上述的形式语言与西方逻辑中通常所用的语言并无二致,然而,形式语言背后的意趣,所要关注的对象、问题等却有着很大的差异。例如,在亚里士多德的词项语言中,变元符号、谓词符号分别代表现实世界的个体事物及其属性等,其意趣在于企图沟通认知世界和现实世界,认为它们是可以一一对应的,于是,它关注真假,一个句子的真假,就是在现实世界中存在一个与其对应的事实。这里,新因明的形式语言所要刻画的是认知世界,或概念、名相世界,而不是现实世界。新因明认为我们的知识来源只有两种:现量和比量,前者是亲证,直接认识,不需要推理,其认识对象是自相,认识结果是离分别、名相等;(11)陈那:《集量论略解》,载于法尊译编:《大藏经补编》第9册,北京:中国社会科学出版社,1982年,第343页。后者正相反,是间接认识,需要推理,其认识对象是共相,认识结果是分别、名相等。(12)陈那:《集量论略解》,第342页。虽然现量决定比量,但比量终究不是现量。由于没有认知世界与现实世界一一对应的这个强假设,自然也就不关注真假,具体表现为新因明的形式语义学缺少真值定义部分。因此,它关注的是推理,概念间、句子间的推理,其意趣在于破邪立正。称一个句子或认识是邪的,是指由它能导致认知主体在认识上的自相矛盾。反之,称一个句子或认识是正的,是指由它不会导致认知主体在认识上的自相矛盾。
(二)基本语句
(三)矛盾语句及矛盾语句集
2.包含矛盾语句的语句集是矛盾语句集。
(四)信念集
对认知主体的信念的整体,用语句集Σ表示,简称为信念集。由于一个正常人是不可能自相矛盾的,所以他的信念集就不会包含矛盾语句。信念集总是关于不同认知主体的信念,由于共业和别业的关系,使得不同信念集之间存在着共性和差异性。共性表现在常识,世间共许;差异性则表现在闻道有先后,术业有专攻。
(五)认知主体对语句的态度
认知主体对语句的态度要么相信,要么不相信,要么悬置。
1.如果α∈Σ,则表示认知主体相信α;
我们的交流总是离不开认知主体,也就是说语句总是认知主体的信念集里的语句。当我们谈论某主体信念集中的简单语句α或α时,我们实际上是在谈论该主体相信或不相信α。这与西方逻辑的基本假设是不同的:西方逻辑中有一个隐含的存在性假设,即词有其相对应的对象,不含命题态度的语句有其相对应的客观事实。如果将我们这套简单语句转换为西方逻辑的语句,则相当于西方逻辑中含有一个命题态度的语句。
(六)四种基本语句与认知主体间的对当关系
四种基本语句对于认知主体而言存在着如下的对当关系(如图1),设Σ为其信念集:
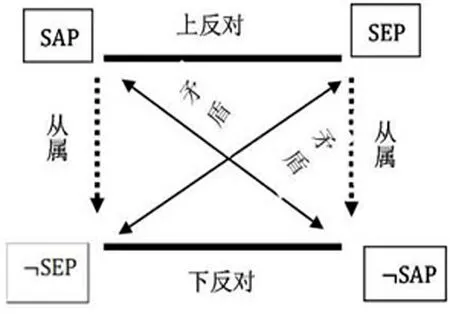
图1
3.SΑP与SEP是上反对关系,允许同时不成立,但不允许同时成立。意思是,某人不可能相信SΑP的同时,又相信SEP;但是他可以既不相信SΑP,也不相信SEP。
(七)信念框架
由于概念、语句是一定生存共同体所使用的,所以,共许对于语言概念、名相世界来说极为重要,是推理、辩经、教化过程中所遵循的一条非常重要的非逻辑规则。所谓共许,就是共同认可、共同许可,即共识。同时,信念集是认知主体对语句,甚至是对概念的理解,因此,这些信念就不可能是杂乱无章地堆积,必将以一定的关系形式构成有机整体。我们就将这个整体,即信念集及其关系统称为信念框架。
概念、信念之间可以是以一种或多种的关系存在,古因明论师将相似关系运用于日常的推理、论辩之中。例如,运用瓶等的所作性与声的所作性间的相似性作类比,从而得出声应与瓶一样具有无常性。这种推理形式就是类比推理,广泛存在于“五支作法”这一论辩形式之中。由于类比推理根本无法揭示两个概念之间的关系,所以不能为论辩提供坚实的逻辑基础。(13)许春梅:《从十四过类角度探究新因明的创新与贡献》,《世界宗教文化》2020年第3期,第147—150页。新因明通过九句因理论解决了古因明在这方面存在的问题,并给出了一般方法,能任意探讨两概念间的关系。(14)许春梅:《九句因理论的形式语义学》,《逻辑学研究》2018年第4期,第110页。又通过因三相理论解决了何种因能必然地推出宗的问题,因第一相保证了因包含有法,因第二、三相保证了所立法包含因,于是就必然地有所立法包含有法,宗得证。“若三相成就,即说为正因。”(15)陈那:《集量论略解》,第367页。即具备这三相的因就能推出宗。一般地,有法、因法与所立法这三个概念,如果满足了这三相,则它们之间是传递关系。反之,如果它们之间有传递关系,则它们满足这三相。如此,新因明一般地、形式化地揭示出概念间的内在逻辑关系,从而为推理、论辩提供坚实、可靠的逻辑基础。在这里,实际上有一个假设,即智者总是对其信念极其自信,因为凡成为其信念的语句必然是能经得起逻辑推理,而且其概念之间是以传递性关系存在。这么一来,不论是推理,还是辩论、教化,其关键都在因三相,一旦将其悟出或是明示,则推理成立,辩论成功,这就是所谓“比二类:为自比量及为他比量。此中,为自,三相因观义;为他比量者,显自所观义。”(16)陈那:《集量论释略抄》,吕澂译编:《大藏经补编》第9册,北京:中国社会科学出版社,1982年,第191、199页。下面,我们将根据这种传递关系的信念集来构建信念语义框架,并在此基础上讨论一些问题。
定义1 (Σ-信念语义框架)我们称<Σ,R>是信念语义框架,当且仅当:
(1)Σ是一个公式集;
(2)R:Σ×Σ→Σ ,是Σ上的传递关系,即对任意α∈Σ,都存在β、γ,使得R(β,γ)=α。
定义2(满足)我们称<Σ,R>是信念语义框架,α是语句,Σα定义如下:
例1 考虑某主体的信念语义框架<{并非鸟会飞、企鹅是鸟、……},R>,问语句“企鹅会飞”能否成为该主体的信念?
答:不能。由于“并非鸟会飞”是该主体的信念,所以,不存在R(企鹅是鸟,鸟会飞)=企鹅会飞,即“企鹅会飞”∉Σ,该主体不相信企鹅会飞。如不然,主体相信语句“企鹅会飞”,则将导致该主体自相矛盾,这是不允许的,因此主体不可能相信该语句。
例2 考虑某主体的信念语义框架<{凡所作皆无常、声是所作、……},R>,问语句“声无常”能否成为该主体的信念?
答:能。由于“凡所作皆无常”和“声是所作”是该主体的信念,存在R(凡所作皆无常,声是所作)=声无常,即语句“声无常”不会导致主体自相矛盾,因此,它有可能为该主体接受。
定理1 给定公式α,如果存在β、γ∈Σ,使得R(β,γ)=α,则α∈Σ。
2.3 分娩方式 高龄组(高龄初产、高龄经产)剖宫产率54.6%(20 875/38 255)明显高于非高龄组的35.5%(69 694/196 508),差异有统计学意义(P<0.05)。见表3。
证明:由Σ-信念语义框架定义可得。
上述定理说明,凡能经得起逻辑推理的语句,都有可能为我们所接受。
定理2 给定公式α,如果{α}∪Σ是一致的,则存在β、γ∈Σ,使得R(β,γ)=α。
证明:如不然,则不存在β、γ∈Σ,使得R(β,γ)=α,于是α∉Σ,由满足定义,即Σα再由传递性,{α}∪Σα,由于{α}∪Σα,因此,{α}∪Σ不一致。
这个定理说明,凡能被接受的语句,一定是能经得起逻辑推理。逻辑是不同地域、根基的众生所共许,共同遵守的基本原则。瑜伽行派要使不同根基的众生都能接受某教义,最起码它能经得起逻辑的推敲,这也正是新因明要为三支论辩模式寻找坚实、可靠的逻辑基础的根本出发点。
这个定理说明如果接受一个新语句会导致矛盾,则说明该语句与我们的认知是不相容的;反之,如果一个新语句与我们认知是不相容的,则接受它必将导致矛盾。
定理4 Σ不一致,则存在有穷公式序列集Φ,Φ⊆Σ,使得Φδ且Φδ。
证明:略
(八)辩经的形式语义学
定义3 (Γ-二叉树)我们称<Γ,R>是二叉树,当且仅当:
(1)Γ是由n(n≥1)个有限节点组成一个具有层次关系的集合,且Γ⊆Σ;
(2)没有父节点的节点称为根节点;
(3)每个非根节点有且只有一个父节点;
(4)每个节点只有两个不相交的子树;
(5)R:Γ×Γ→Γ ,是Γ上的传递关系,即对任意α∈Γ,存在两个公式β、γ,使得R(β,γ)=α。
上述定义有几层含义:首先,(1)指出了在实际的推理中,我们总是运用有限的概念、语句。因此,虽然我们不清楚自己整个信念集有多大,脑中有多少知识,但是它对于我们实际生活似乎并无多大妨碍;其次,(5)说明了其推理是建立在具有传递关系的信念框架之上;第三,如果我们把被推理出来的公式称为父节点,把推出其它公式的公式称为子节点,把不再推出其它公式的公式称为根节点,即(2)、(3)以及(4)每个子节点至多只有两个不相交的子树,那么<Γ,R>信念框架类似于二叉树。如下图2:
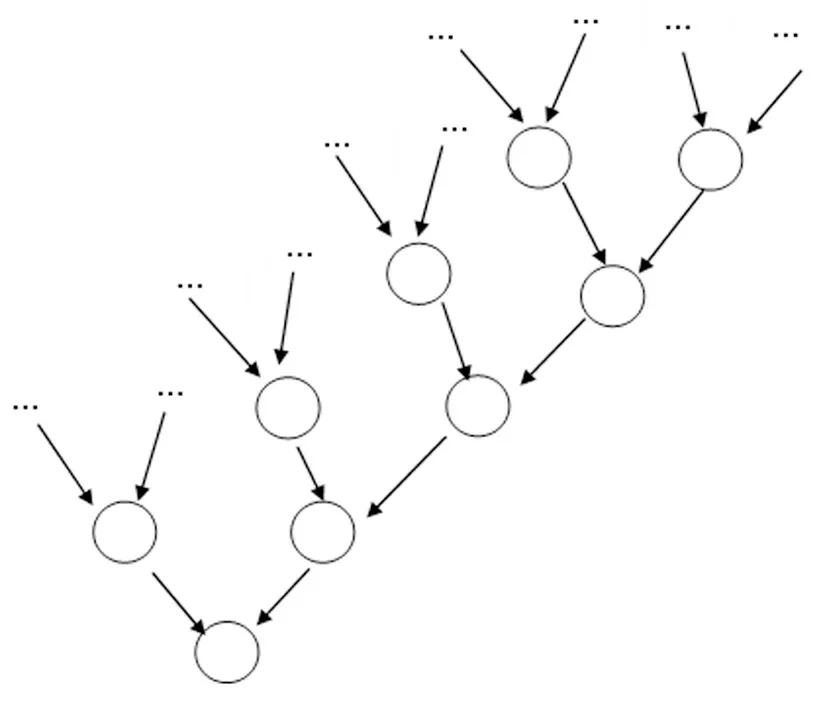
图2
最后,每次推理都可以构造成二叉树,二叉树不同,则其根节点不同。于是,我们就可以根据根节点之间是否矛盾,来判断信念集是否一致、自洽。
为了使用方便,我们还将定义两个概念:“结点的层次”和“树的高度”:
定义4 (结点的层次)我们用数学归纳法定义结点的层次:
(1)根结点的层次为1;
(2)设某父节点的层次为κ,则其子节点的层次为κ+1。
定义5 (树的高度)我们称树中结点的最大层次为树的高度。
新因明将比量分成为自比量和为他比量。(17)法尊译本称其为“自义比量”和“他义比量”;吕澂译本则称其为“为自比量”和“为他比量”。前者,“自义,三相因见义”(18)陈那:《集量论略解》,第29页。指的是“由具足三相之因,观见所欲比度之义。”(19)陈那《集量论略解》,第29页。后者,“他义比量者,善显自见义。”(20)陈那:《集量论略解》,第60页。即通过某种特殊的论式、格式,很好地将自己所悟呈现给对方,从而使其生正解、开悟。它们的关键都在于因上,前者谈的是何种因能推出结论,而后者谈的则是如何寻找能为对方接受的正确的因。新因明指出唯有因三相,即具有传递关系的推理结构,就是前面所定义的Σ-信念语义框架,更具体些,就是Γ-二叉树,它是为自比量的推理模型,也是为他比量的依据。Γ-二叉树说明了推理一步一步是如何符合逻辑,前提是如何必然得出结论;将整个Γ-二叉树倒着向他人说出时,又是一种教化的过程。因此,辩论应该包含这样的两个过程:一、结论如何必然得出的过程,如图2;二、怎样将“结论如何必然得出的过程”向他人说明的过程,其模型是倒Γ-二叉树,如下图3:
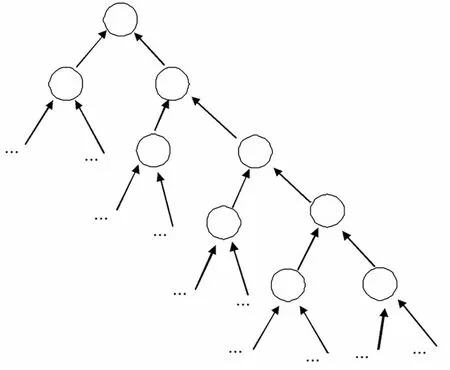
图3
定义6 (好辩论)我们称一个辩论是好的,当且仅当:
(1)存在不一致、不自洽的信念集;
(2)能找出两个二叉树使得它们的根节点相互矛盾。
辩经之所以能发起,在于立论者有欲知欲,在形式语义上我们是通过“不一致”、“不自洽”这个概念来实现。辩论者又恰好有智慧,能找到一个反例,在立论者信念下能推出两个互相矛盾的信念,即两个根节点相互矛盾的二叉树。于是整个辩经就有结果,辩论者就辩赢了,达到了教化的目的。
定理4 Γ不一致,当且仅当,存在两个Γ-二叉树,使得它们的根节点相互矛盾。
证明:Γ不一致,当且仅当,存在有穷公式集Γ1、Γ2,Γ1⊆Γ、Γ2⊆Γ,使得Γ1σ、Γ2σ,由满足定义,σ∈Γ1,σ∈Γ2,根据Γ-二叉树定义,则有以σ为根节点的Γ1-二叉树和以σ为根节点的Γ2-二叉树。又因Γ1⊆Γ、Γ2⊆Γ,σ与σ相互矛盾,根据集合传递性,因此,存在两个Γ-二叉树,使得它们的根节点相互矛盾。
定理5 Γ一致,当且仅当,不存在两个Γ-二叉树,使得它们的根节点相互矛盾。
证明:略
定理6 给定公式α,{α}∪Γ不一致,当且仅当,存在两个{α}∪Γ-二叉树,使得它们的根节点相互矛盾。
证明:{α}∪Γ不一致,当且仅当,存在有穷公式集Γ1、Γ2,Γ1⊆Γ、Γ2⊆Γ,使得{α}∪Γ1σ、{α}∪Γ2σ,由满足定义,σ∈{α}∪Γ1,σ∈{α}∪Γ2,根据Γ-二叉树定义,则有以σ为根节点的{α}∪Γ1-二叉树和以σ为根节点的{α}∪Γ2-二叉树。又因Γ1⊆Γ、Γ2⊆Γ,σ与σ相互矛盾,根据传递性,因此,存在两个{α}∪Γ-二叉树,使得它们的根节点相互矛盾。
定理7 {α}∪Γ一致,当且仅当,不存在两个{α}∪Γ-二叉树,使得它们的根节点相互矛盾。
证明:略
上述这些定理说明了,这里不关乎信念的对错与否,或者说这个形式语义说明:只要是不一致、不自洽的信念集,则必然推出矛盾,则必然存在两个二叉树,使得它们的根节点相互矛盾。而一旦将这两个二叉树呈现出来,则辩论就赢了,否则辩论就没法赢。
(九)辩经形式语义学在“红白”颜色之辩中的运用
有了这套辩经形式语义学,就很容易对“红白”颜色之辩中给出一个直观的描述,如下图4和图5:
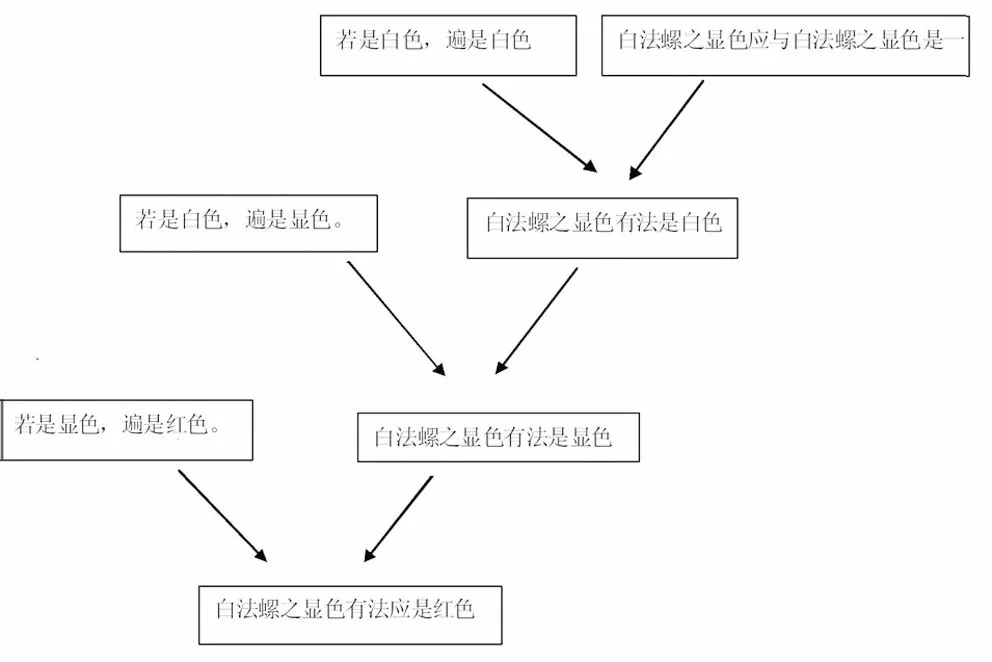
图4
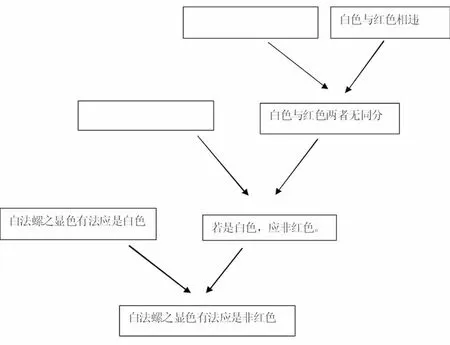
图5
图4,此二叉树高度为4,任一层两子节点上的公式都能逻辑地必然推出其父节点上的公式,其推理形式满足三段论的AAA式。这棵Γ-二叉树,从树根到树顶是表中从(1.1)至(1.3)部分,是寻找可为对方接受的因的过程;反过来,从树顶到树根则是表中从(2.1)至(2.4)部分,是根据前面所找的因而进行推理的过程。
图5,此二叉树高度为4,任一层子节点上的公式都能逻辑地必然推出其父节点上的公式,其推理形式满足三段论的AAA式。这棵Γ-二叉树,从树根到树顶是表中从(3.1)至(3.2)部分,是寻找可为对方接受的因的过程;反过来,从树顶到树根是表中从(4.1)至(4.3)部分,是根据前面所找的因而进行的推理过程。
如果我们将树顶到树根的叙述称为正向叙述,将树根到树顶的叙述为反向叙述,那么图4、图5这两棵二叉树的正、反向叙述就是红、白颜色之辩的整个辩经过程。根据这两棵二叉树的根节点之间是相互矛盾的,就可知如果承许立论者所立的主张“若是显色,遍是红色”,则势必会导致信念集的不自洽、不一致。正因为如此,(5.1)、(6.1)和(6.2)是敌论者认识到了其观点的错误所在,并承认“白法螺之显色有法”是一个有效的反例。
四、结论
综上所述,本文通过形式语义学的方法,以新因明为指导思想,建立了一套更为直观的辩经语义学。这套模型语义解释,不仅适用于藏传辩经,而且有助于我们深入研究新因明在辩经中的运用。
首先,藏传辩经的模型是二叉树的正、反向叙述,集合了找正因和推理这两方面于整个辩经过程。一个好的辩经就是有结果、有输赢的辩经,本质上就是能找到两棵在根节点上相互矛盾的二叉树。
其次,研究表明新因明在辩经中有着重要的运用,具体表现至少有如下几个方面:
第一,九句因理论为我们提供了一种探讨任意两概念间内在逻辑关系的范式,即任意两概念要么具有相容关系,要么不具有相容关系。其中,相容关系又有两种:包含和相交。这种思维方法运用在辩经中的一个典型表现就是立论者在回答应成式时,一般是按照有法、所立法和因三者之间两两概念的关系来探讨:(1)如果有法包含于所立法,则承许;如不然,则转向考察有法与因的关系。(2)如果有法包含于因,则因成立;如不然,则因不成,继而再转向考察因与所立法之间的关系。(3)如果因包含于所立法,则周遍;如不然,则不周遍或周遍相违。
第二,因三相理论揭示了因明推理中正因所应具备条件,即有法必须包含于因,且因又包含于所立法。这在辩经中一方面有利于辩论者建立有利于推理的应成式;另一方面有利于立论者快速识别正误与作答。
第三,新因明将比量二分,明确区分悟者与被悟者。自悟方能悟他,而自悟唯有现量和比量(或推理)可达到,但悟他则需要悟者对他者的认知有所洞见,又能照顾对方的情绪,有耐心,循循善诱,还要有较好的媒介,将“何以如此”的整个推理过程呈现。这在辩经中主要表现在寻找对方认可的因的过程,以及根据所找因进行推理的过程。
