2022年北京大学强基计划数学试题及其详解
2023-07-30甘超一
甘超一
(华南农业大学资源环境学院2019级环境科学2班,广东 广州 510642)
1.满足正整数n≤2022且2n+1与3n+1均为完全平方数的n的个数是( ).
A.0 B.1 C.2 D.以上均错
解析设2n+1=(2k+1)2(k∈N*),可得n=2k(k+1)≤2022,k≤31.
还可设3n+1=6k(k+1)+1=5(k2+k)+(k2+k+1)=l2(l∈N*),所以k2+k+1≡l2≡0,1,4(mod5),进而可得k≡0,4(mod5).
再由k∈N*,k≤31,可得k只可能取12个值:4,5,9,10,14,15,19,20,24,25,29,30.
再由6k(k+1)+1=l2(l∈N*),可得k=5,l=11,再得n=40,所以满足题设的n的个数是1.
2.满足∠ACB=∠CAD=40°,∠ABD=∠BDC=50°且两两不相似的凸四边形ABCD的个数是( ).
A.1 B.2 C.3 D.以上均错
解析在凸四边形ABCD中,由∠ACB=∠CAD,可得AD∥BC;同理可得AB∥CD.所以凸四边形ABCD是平行四边形.
在△OAB与△OBC中,由正弦定理可得
2sinθcosθ=2sin40°sin50°,
sin2θ=sin80°(0°<θ<90°),
所以θ=40°,50°.
所以满足题设的凸四边形ABCD的个数是2.
3.满足正整数y≤2022且100|2y+y的y的个数是( ).
A.16 B.18 C.20 D.以上均错
解析可得22|2y+y,再得2|y,又得4|y,可设y=4x(x∈N*,x≤505).
因而题设即25|24x+4x,25|(5×3+1)x+4x(x∈N*,x≤505).
由5|(5×3+1)x+4x(x∈N*,x≤505),可得5|1+4x,5|x-1(x∈N*,x≤505),因而可设x=5z+1(z∈N,z≤100).
因而题设即25|220z+4+20z+4,25|4(220)z+5z+1(z∈N,z≤100).
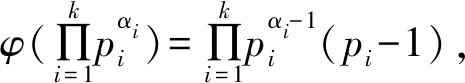

A.320 B.321 C.322 D.以上均错
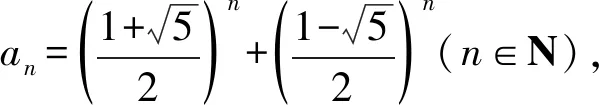
注该题解答中的数列{an}就是数学史上著名的卢卡斯数列.
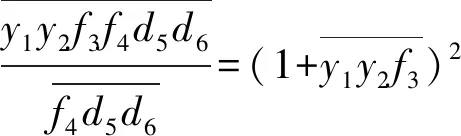
A.2 065 020 B.2 066 020
C.2 067 020 D.以上均错
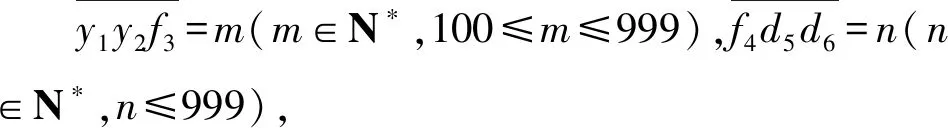
再由m∈N*,102≤m+2≤1 001,可得n∈N*,n≤9,n|1 000,所以n=1,2,4,5,8.
进而可求得(m,n)=(998,1),(498,2),(248,4),(198,5),(123,8),所以满足题中条件的六位数1 000m+n共五个:998 001,498 002,248 004,198 005,123 008.可求得它们的和是2065 020.
6.满足a,b,c,d∈Z且a+b+c+d=6的正整数ab+ac+ad+bc+bd+cd的取值个数是( ).
A.10 B.20 C.30 D.以上均错
解析由柯西不等式,可得(12+12+12+12)·(a2+b2+c2+d2)≥(1a+1b+1c+1d)2=36,a2+b2+c2+d2≥9.
由恒等式2(ab+ac+ad+bc+bd+cd)=(a+b+c+d)2-(a2+b2+c2+d2),及题设a,b,c,d∈Z且a+b+c+d=6,可得2|a2+b2+c2+d2.
下证8⫮ (a2+b2+c2+d2).
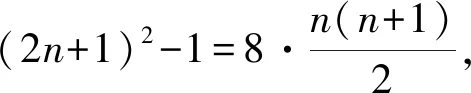
进而可得:当a,b,c,d中的奇数个数是1,2,3时,均可得4⫮ (a2+b2+c2+d2),所以8⫮ (a2+b2+c2+d2);当a,b,c,d中的奇数个数是4时,可得8⫮ (a2+b2+c2+d2).
当a,b,c,d中的奇数个数是0,即a,b,c,d全是偶数时,可设a=2a′,b=2b′,c=2c′,d=2d′(a′,b′,c′,d′∈Z),得a′+b′+c′+d′=3.再由恒等式
(a′+b′+c′+d′)2=a′2+b′2+c′2+d′2+2(a′b′+a′c′+a′d′+b′c′+b′d′+c′d′),
可得2⫮ (a′2+b′2+c′2+d′2),8⫮ [(2a′)2+(2b′)2+(2c′)2+(2d′)2],8⫮ (a2+b2+c2+d2).
所以8⫮ (a2+b2+c2+d2).
所以本题即求满足a,b,c,d∈Z且a+b+c+d=6,10≤a2+b2+c2+d2≤34,2|a2+b2+c2+d2,8⫮ (a2+b2+c2+d2)的整数a2+b2+c2+d2取值个数.
再由1+1+2+2=6,12+12+22+22=10,0+2+2+2=6,02+22+22+22=12,0+1+2+3=6,02+12+22+32=14,0+0+3+3=6,02+02+32+32=18,(-1)+1+3+3=6,(-1)2+12+32+32=20,(-1)+1+2+4=6,(-1)2+12+22+42=22,(-1)+0+3+4=6,(-1)2+02+32+42=26,(-2)+2+2+4=6,(-2)2+22+22+42=28,(-2)+1+3+4=6,(-2)2+12+32+42=30,(-2)+1+2+5=6,(-2)2+12+22+52=34,所以所求答案是10.
7.满足AB=1,BC=2,CD=4,DA=3的凸四边形ABCD的内切圆半径的取值范围是( ).


证明连接凸四边形ABCD的对角线BD,在△ABD与△CBD中,分别由余弦定理可得
a2+d2-2adcosA=BD2=b2+c2-2bccosC.
①
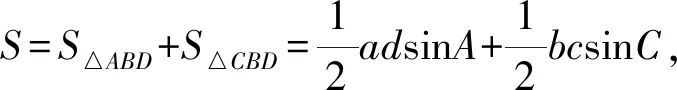
进而可得引理成立.
再来解答本题.

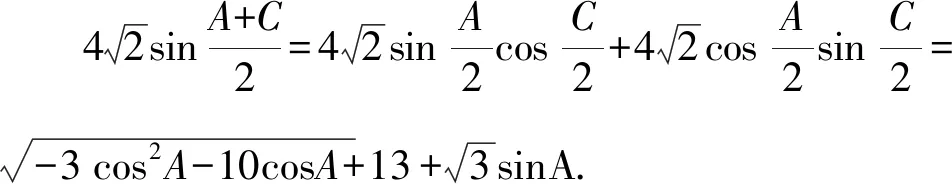

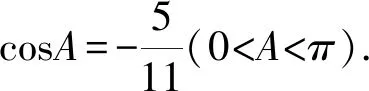

8.已知三个复数z1=(5-a)+(6-4b)i,z2=(2+2a)+(3+b)i,z3=(3-a)+(1+3b)i(a,b∈R).若|z1|+|z2|+|z3|取最小值,则3a+6b=( ).
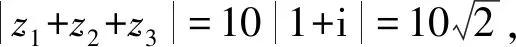

A.12+π B.12-π C.12-2π D.以上均错



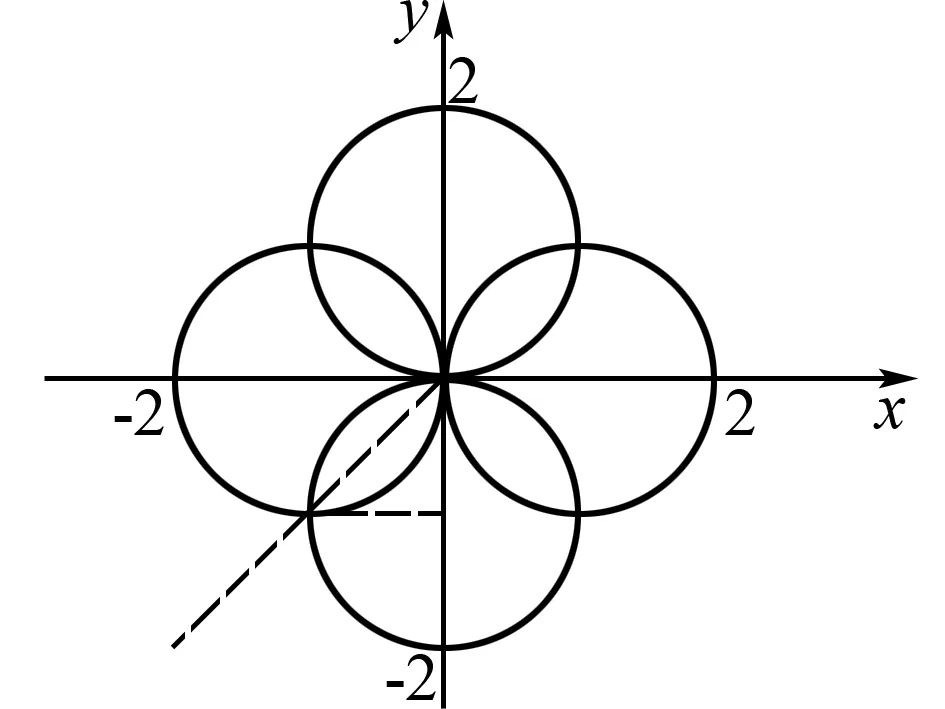
图1 第9题图
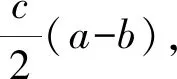
A.3 B.2 C.1 D.以上均错
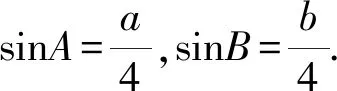




C.(0,1] D.以上均错
解析如图2所示,连接AM.由题设,可得∠ADM=180°-∠BCD=180°-∠ABM,所以A,B,M,D四点共圆,再得∠BAM=∠BDM.

图2 第11题图
在△ABM中,由正弦定理可得


A.3 B.9 C.18 D.以上均错
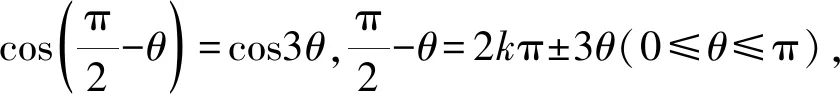

A.730 B.520 C.370 D.以上均错
解析可得A<10n+1,1≤D(A)≤9(1+2+22+…+2n)=9(2n+1-1)<10·2n+1(n∈N).
由b0<1040,可得b1=D(b0)<10·240<10·814<1015;再得b2=D(b1)<10·215=10·85<106;又得b3=D(b2)<10·26=640<103;又得b4=D(b3)<10·23=80<102;又得b5=D(b4)<10·22=40<102;…进而可得正整数b2022是一位数或两位数,所以b2022的各位数字的平方和不超过92+92=162,因而本题的答案是D.
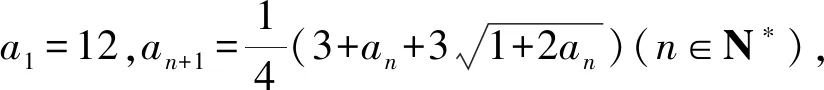
A.2 B.4 C.8 D.以上均错


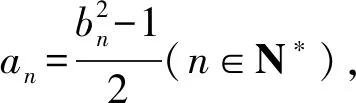
所以与a10最接近的整数是4.
15.已知数列{ak}1≤k≤5的各项均为正整数,且|ai+1-ai|≤1(i=1,2,3,4).若数列{ak}1≤k≤5中存在一项是3,则数列{ak}1≤k≤5可能的个数是( ).
A.211 B.243 C.387 D.以上均错
解析(1)若a1=3,由题设可列出表1,进而可得满足题设的数列共75个:
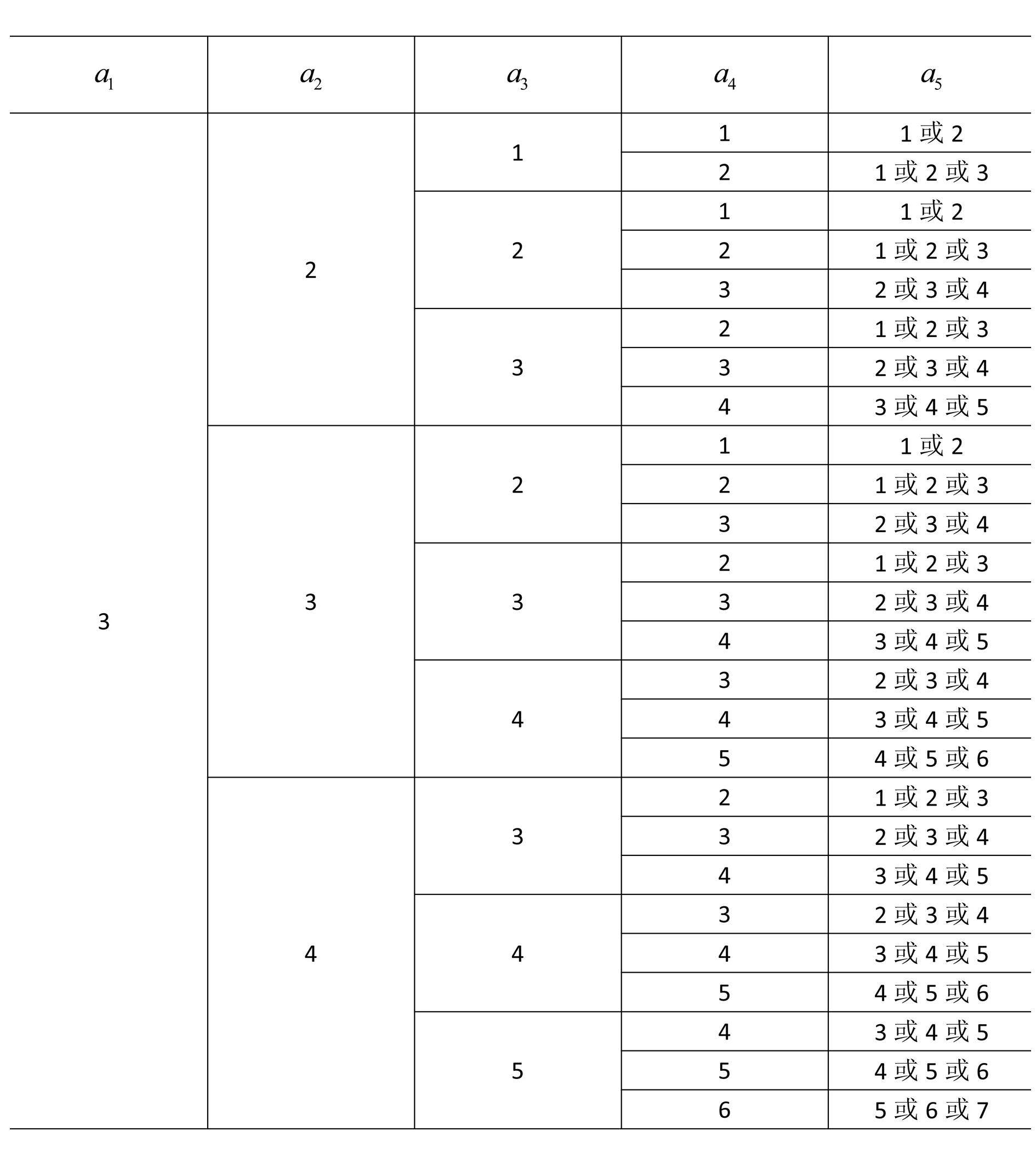
表1 15题表
(2)若a1≠3且a2=3,可得a1=2或4.由题设还可列出表2(数列a2,a3,a4,a5共26个),进而可得满足题设的数列共2×26=52个:
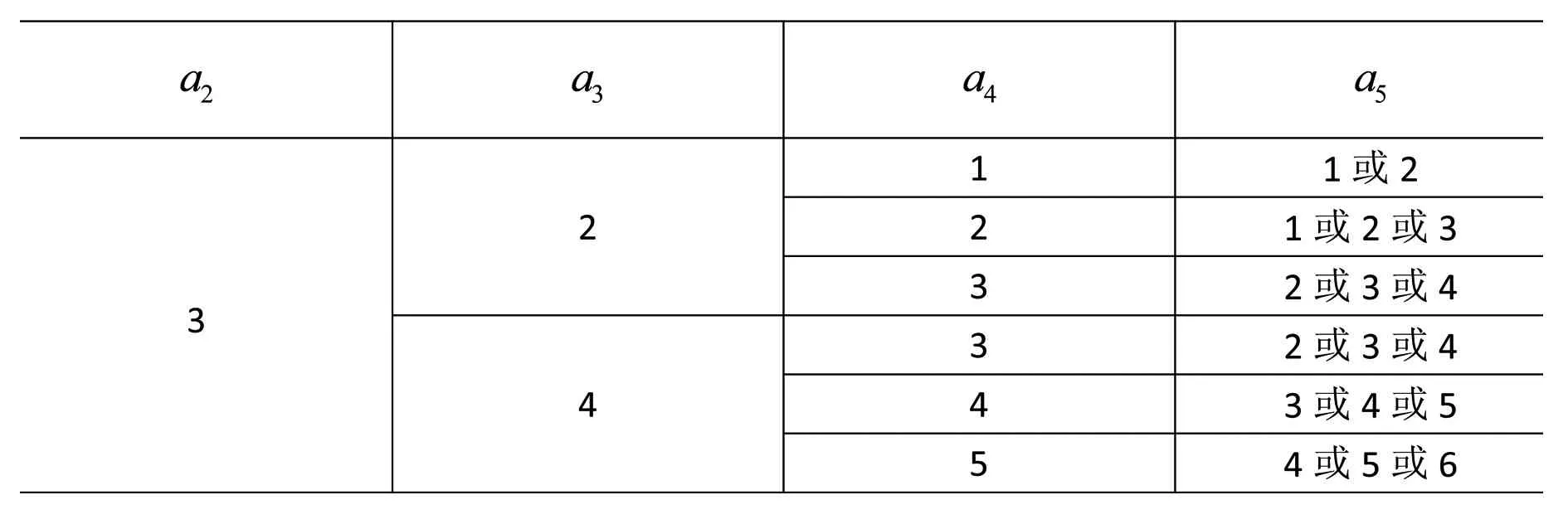
表2
(3)若a1≠3,a2≠3且a3=3,可得a2=2或4.当a2=2时,a1=1或2;当a2=4时,a1=4或5.所以数列a1,a2,a3共2×2=4个.
若a3=3,可得a4=2.同理可得数列a3,a4,a5共3×3=9个.
进而可得满足题设的数列共4×9=36个.
(4)若a1≠3,a2≠3,a3≠3且a4=3,可得a5=2或3或4,所以满足题设的数列共27个.
(5)若a1≠3,a2≠3,a3≠3,a4≠3且a5=3,满足题设的数列共21个.
综上所述,可得所求答案是75+52+36+27+21=211.

A.12 B.24 C.36 D.以上均错
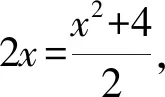


17.将12个正整数1,2,3,…,12分别放入6个两两交集为空集的二元集合中,要求每个集合中的两个元素互质,则不同的分法种数是( ).
A.252 B.302 C.352 D.以上均错
解析因为2,4,6,8,10,12这6个偶数两两不互质,所以它们应分别在题设中的6个集合(设为Y2,Y4,Y6,Y8,Y10,Y12)中(各放一个).还可得5∉Y10;3,9∉Y6;3,9∉Y12;1,7,11可任意放入上述6个集合中(但要满足这6个集合均是二元集合).
接下来,再看6个奇数1,3,5,7,9,11如何放?分下面两种情况:
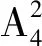

综上所述,可得所求答案是144+108=252.
18.已知m,n,k∈N*,若f(x)=(1+x)m+(1+x)n+(1+x)k的展开式中x的系数是10,则f(x)的展开式中x2系数的最大值与最小值之和是( ).
A.20 B.30 C.40 D.以上均错
解析由题设可得m+n+k=10(m,n,k∈N*),f(x)的展开式中x2的系数是
由柯西不等式,可得(12+12+12)(m2+n2+k2)≥(1m+1n+1k)2=100.
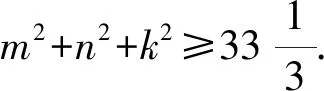
再由m,n,k∈N*,可得m2+n2+k2≥34.
又因为当(m,n,k)=(3,3,4)时,m2+n2+k2=34,所以(m2+n2+k2)min=34.
可得a2+b2≤12+(a+b-1)2⟺(a-1)(b-1)≥0,所以有不等式a2+b2≤12+(a+b-1)2(a,b∈N*).
所以m2+n2+k2≤12+(m+n-1)2+k2≤12+12+(m+n+k-2)2=12+12+82=66.
再由当(m,n,k)=(1,1,8)时,m2+n2+k2=66,所以(m2+n2+k2)max=66.
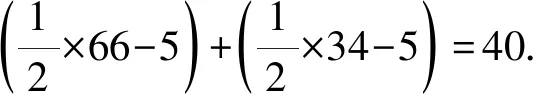
19.若△ABC的各边长依次成等差数列,则cosA+cosB+cosC的取值范围是( ).
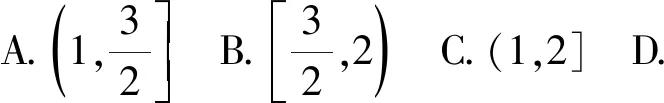

进而可求得答案.



证明由点差法可证得 “圆或椭圆内除中心外的点是唯一一条弦的中点”[1],由此可再证得结论.
椭圆内接平行四边形的中心就是该椭圆的中心.④
因而可设菱形Ω各顶点的坐标分别是A1(acosα,bsinα),A2(acosβ,bsinβ),A3(-acosα,-bsinα),A4(-acosβ,-bsinβ)(0≤α<β<π+α<π+β<2π)(即0≤α<β<π),且得|A1A2|=|A1A4|,即
b2sinαsinβ=-a2cosαcosβ.
⑤

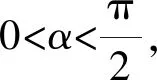
进而可得欲证结论成立.
