例谈质心和质心系在解题中的应用
2023-07-30陈新学
陈新学
(杭州学军中学教育集团文渊中学,浙江 杭州 311200)
质心是力学的一个重要概念,一些看似复杂的力学问题,如果应用质心的相关知识分析,解题思路会变得清晰,解题过程会变得简单.本文借助于几个典型问题探讨质心的概念、质心运动定理以及质心参考系在解题中的应用.
1 质心的相关概念
1.1 质心和质心运动定理
设N个质点组成的系统(简称质点系或系统)中,各质点的位置矢量(简称位矢)分别为r1,r2,…,rN,定义此质点系的质心的位矢
(1)
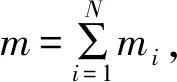
式(1)两边对时间求导得质心的速度
(2)

可知质点系的总动量等于质心的动量.式(2)两边对时间求导得质心的加速度
(3)
在惯性系中,对于质点系,由牛顿第二定律可得

(4)
其中F外为质点系所受到的外力的矢量和,由式(3)和式(4)得
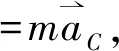
(5)
由式(5)知,质心的加速度由质点系受到的外力的矢量和确定,与质点系的内力无关,这个结论称为质心运动定理.
1.2 质心参考系
质心参考系是指相对质心不动的参考系,简称质心系.如果质心相对惯性系做匀速直线运动,则质心系也是惯性系;如果质心相对惯性系做加速运动,则质心系是非惯性系.
2 例题
例1 在光滑的水平面上放一半径为a、质量为M的圆环,在某一瞬间有一质量为m的甲虫由静止开始沿此圆环爬行.求甲虫及圆环中心的运动轨迹.
解析甲虫和圆环组成的系统受到的外力的矢量和为0,且甲虫和圆环的初状态都是静止的,根据质心运动定理知,甲虫和圆环组成的系统的质心静止不动.甲虫沿圆环爬行,甲虫到圆环中心的距离不变,始终为圆环的半径,故甲虫、圆环中心到质心的距离都不变,分别为
即甲虫、圆环的中心的轨迹都是圆.以系统质心为坐标原点,甲虫的轨迹方程为
圆环中心的轨迹方程为
例2 一块长为L的大平板静放在光滑水平面上,一小孩骑着儿童自行车(小孩和车的大小可忽略不计)以v0的速度从板的一端驶上平板,在板上他的速度忽快忽慢,在将近板的另一端时,他突然刹车,停在板端.已知人在板上骑车的时间为t,板的质量为M,小孩与车的总质量为m.求从车驶上平板到车相对板刚静止时板的位移[1].

图1 例2示意图
例3如图2所示,用劲度系数为k的轻弹簧连接放在光滑水平面上质量分别为m1、m2的木块.让第一个木块紧靠竖直墙,在第二个木块的侧面上施加水平压力,将弹簧压缩L长度,撤去这一压力后,求系统质心可获得的最大加速度值和最大速度值.

图2 例3示意图
解析由质心运动定理知,外力的矢量和最大时,质心的加速度最大.分析可知刚撤去压力时,弹簧弹力最大,竖直墙施加的外力最大,大小为kL,所以系统质心可获得的最大加速度为
此后弹簧弹力减小,系统质心做加速度减小的加速运动,直至木块m1离开墙,系统质心开始做匀速直线运动,所以木块m1刚离开墙时系统质心的速度最大,设此速度为vCm,从撤去压力到木块m1刚离开墙,系统的机械能守恒:
其中v2为木块m1刚离开墙时木块m2的速度,得
由式(2)得系统质心的最大速度
例4 三个等质量物块静止地放在光滑平面上,排成一直线,m1=m2=m3=m,其中m2和m3用弹性系数为k的弹簧相连,并保持自然长度,如图3所示.现在m1以速度v冲向m2,二者发生完全非弹性碰撞,求此后的运动中:

图3 例4示意图
(1)物块m3的最大动能;
(2)物块m2的最小动能[1].

例5如图4所示,长为L、质量线密度为λ的匀质软绳,开始时绳两端A和B一起悬挂在天花板上相距较近的两点.A端的天花板能够提供的最大拉力为1.5λLg,其中g为当地重力加速度.求:
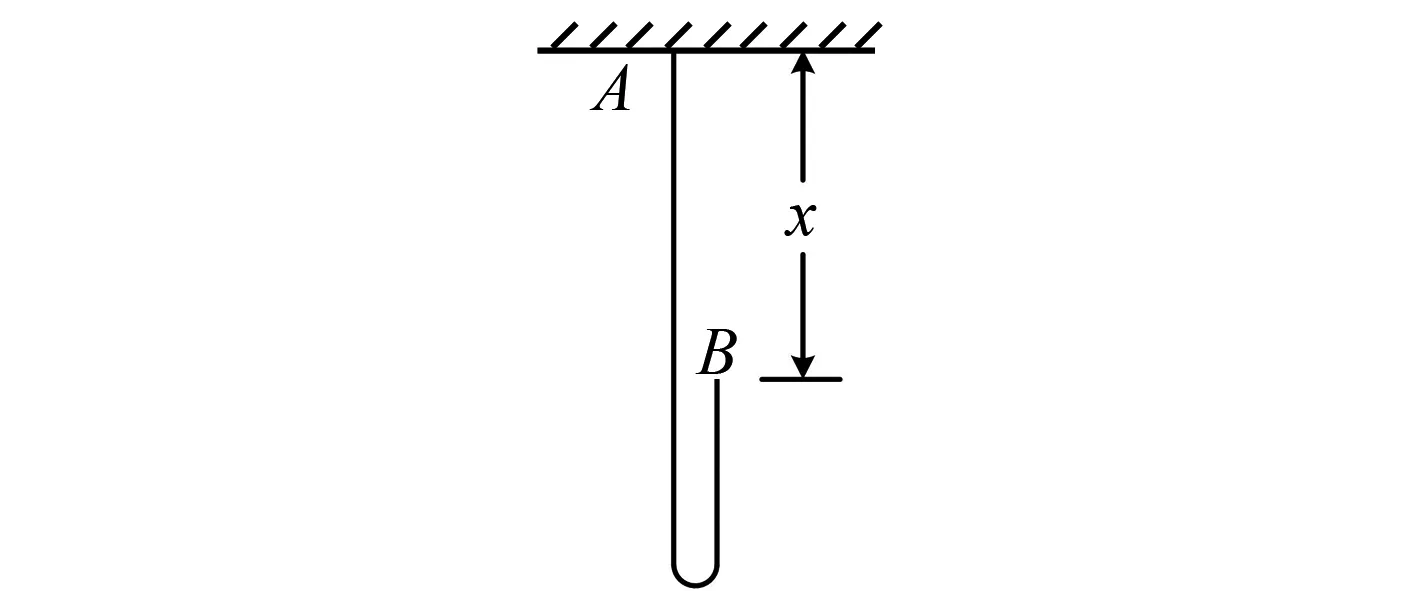
图4 例5示意图
(1)B端下落多长时间后,A端与天花板脱离?
(2)A端与天花板脱离后,经过多长时间绳子完全伸直?
解析(1)以天花板上的A点为原点,竖直向下为正方向建立x轴,B端自由下落x时,右侧绳子质心的速度为
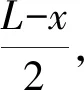
整条绳子质心的加速度

对整条绳子应用质心运动定理得
λLg-F=λLaC,
其中F为天花板对绳子A端的拉力,即

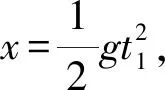

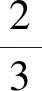
左侧绳子速度为0,应用式(2)得整条绳子质心的速度
此后整条绳子质心和绳子B端都以加度度g向下做直线运动,在质心参考系中,绳子B端做匀速直线运动,B端相对质心的速度


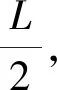

综上所述,应用质心的相关知识解题时,一般先分析系统所受的外力,根据质心运动定理,结合质心的初速度,判断质心的运动情况,再分析各质点或系统的各部分相对质心的运动.在质心系中分析问题时,应注意质心系是惯性系还是非惯性系,如果质心系是非惯性系,受力分析时还要考虑到惯性力.解题时还应注意各物理量的值在质心系和其他惯性系(例如地面参考系)中的区别和联系,计算时不能混淆.
