基于改进复合形法的平流层飞艇外形优化设计
2023-07-29曹胜鸿杨燕初张天晓张航悦
曹胜鸿,杨燕初,张天晓,张航悦
(1. 中国科学院空天信息创新研究院,北京100094;2. 中国科学院大学,北京100190)
1 引言
临近空间(NearSpace)通常是指20~100km的空域,在地球大气中处于平流层和中层,其在环境监测、区域通信、实时监视、预警与导弹防御等领域有很大的应用价值[1]。飞艇是一种轻于空气的航空器,具有垂直起降、长航时、载重大、低能耗、噪声及排放小等特点[2],在临近空间的探测方面具有广泛的应用价值。平流层飞艇是临近空间飞行器的一种,近几十年来,随着航空技术的发展,采用新材料和新技术的大型飞艇得到飞速发展。
因此,有针对性地对平流层飞艇进行优化设计,即多方面考虑飞艇的设计因素就显得尤为重要。平流层飞艇总体设计与优化技术作为方案设计的关键,将会直接决定飞艇系统的整体性能和操控[3]。国内多家研究机构开展了大量的飞艇设计优化工作,例如,中航通飞研究所的秦何军针对飞艇的气动外形进行优化设计[4],中国特种飞行研究所的张超针对重在飞艇低阻囊体进行外形优化[5]。但上述优化设计仅以阻力系数作为优化对象,缺少对飞艇结构因素的考虑。
通过对比分析发现,在改变长细比时,体面比与长细比成正相关,阻力系数与长细比呈现负相关,因此,本文保留阻力、体面比两个飞艇设计因素,建立数学模型,结合实际需求分配两者权重,结合改进的复合形法,构建优化设计框架,通过Matlab软件运算得出艇体长度与艇体最大截面直径,依照实际需求,提供三种合理的飞艇外形设计方案,并结合实际算例仿真分析,验证优化艇形和优化算法的可行性。
2 算法介绍
2.1 飞艇优化程序框架
本文在进行飞艇优化设计过程中,结合最优化设计中的复合形法进行改进,进行目标函数的最优值求解,首先输入原始艇形数据,结合多学科优化设计理念,建立飞艇优化目标函数,并根据实际需求,合理分配各项函数模型的权重,利用Matlab软件结合改进复合形法探索优化值,依照实际需求,有侧重的针对算法所得飞艇长度、飞艇最大截面直径、飞艇长细比进行定向飞艇优化,并提供后期仿真分析的艇形数据,其飞艇优化流程框架如图1所示。需要指出的是,本文所提出的改进复合形算法也可与其它最优值求解方法相结合使用,推广至其它最优值求解问题。
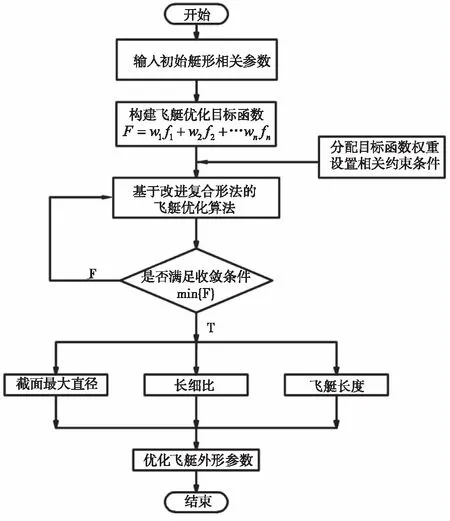
图1 飞艇优化流程框架
2.2 改进复合形法
在约束问题的最优化求解过程中,往往会出现导数和梯度较难求得的情况,尤其是多元函数,甚至会没有明确的工程函数[6]。因此常常采用直接求解的方式,复合形法的基本求解思想是基于无约束最优化问题直接求解方式的单纯形法,仅需在每次扩张、收缩之后验证新得到的点是否在可行域内即可。
单纯形法最早由Spendley、Hext和Himsworth提出[7],后由Nelder和Mead改进成为变型的单纯形法[8],其基本思想是:三点构造单纯形,沿最差点至剩余点所构中心点的方向寻找最差点的替代点,从而构造新的单纯形,其探索过程如图2所示。
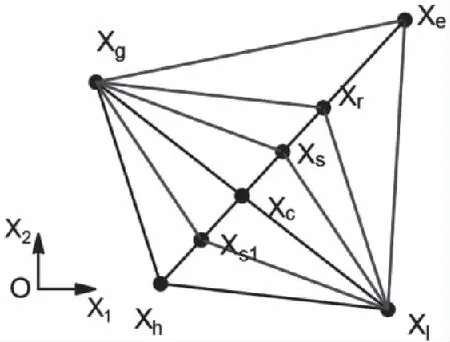
图2 单纯形法探索过程
取三个点并计算其函数值,分析三个点的函数值进行排列得到最差点Xh,次差点Xg最好点Xl,取次差点Xg与最好点Xl的形心Xc,连接最差点Xh与形心点Xc做第一次等步长的扩张得到反射点Xr,若反射点的函数值优于最差点Xh则再进一步扩张,否则,将步长减半,如果新得到的点函数值依旧差于最差点函数值,则直接改变探索方向,其中单纯形法的探索过程,还需要将新得到的点与次差点进行比较,从而考虑新得到点的删减。
经典单纯形法需要计算剩余点所构中心点,并将新得到的点与最差点、次差点进行比较,且随着探索迭代次数的增加,在最优值附近的探索速度较慢,探索步骤缓慢、繁琐,极大地降低了约束问题的求解效率。
单纯形法求解最优化工程函数问题的关键在于单纯形的构建,而在单纯形构建的过程中,选点将会直接影响探索方向的准确性,经典单纯性法求解时需要计算次差点与最好点的形心,并与最差点相连,构成新的探索方向,杨晋提出可以直接连接最差点与最好点构成新的探索方向[9],李庆高在非线性约束问题同样提出直接在最好点与最差点的方向探索得到最差点的替代点[10]。
本文在杨晋单纯形法的基础上进一步改进,提出双向探索的求解思想,即沿着最差点和最好点的方向探索最差点的替代点的同时,沿着次差点和最好点的方向探索次差点的替代点,在两个收敛方向同时求得第二次单纯形的构造点,精简单纯形构造的计算步骤,提高约束问题的求解效率,其探索步骤如图3所示。

图3 改进算法探索过程示意图
改进单纯形法的计算过程如下:
1)取三个点并计算其函数值,分析三个点的函数值并进行排列,从而得到最差点Xh,次差点Xg,最好点Xl,连接次差点Xg与最好点Xl做第一次等步长的扩张,同时连接最差点Xh与最好点Xl做第一次等步长的扩张,如式(1)所示
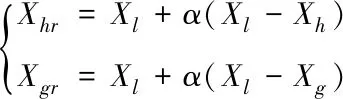
(1)
α:反射系数,单纯形法中通常取为1,复合形法中常取1.3;
Xhr:最差点Xh相对于最好点Xl的反射点;
Xgr:次差点Xg相对于最好点Xl的反射点;
2)分别比较两个反射点与最差点、次差点的函数值,如果反射点函数值小于最差点、次差点的函数值,则说明探索正确,进一步扩张,如式(2)所示

(2)
γ:扩张系数,一般取为2;
Xh4:反射点Xhr相对于最好点Xl的扩张点;
Xg4:反射点Xgr相对于最好点Xl的扩张点;
3)如果反射点函数值比最差点、次差点函数值要大,则减少扩张步长,即收缩。如式(3)所示

(3)
β:收缩系数,一般取为0.5;
Xh2:反射点Xhr相对于最好点Xl的收缩点;
Xg2:反射点Xgr相对于最好点Xl的收缩点;
4)如若收缩点的函数值仍旧大于最差点、次差点的函数值,则说明探索方向有误,改变探索方向,即缩小单纯形,如式(4)所示
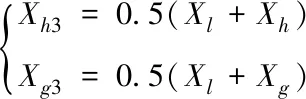
(4)
Xh3:最差点Xh相对于最好点Xl的压缩点;
Xg3:次差点Xg相对于最好点Xl的压缩点;
5)探索所得点与第一次单纯形的最好点构成第二次探索单纯形的三个点,图3所示蓝色线即为第二次单纯形的可能情况。单纯形构造完成后,逐次迭代,直到最好点与形心点几乎为一个点,终止迭代的判据如式(5)所示
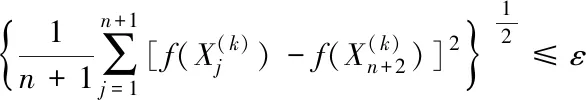
(5)
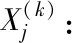
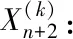
针对收敛性判据,除上述判断形心点与最好点是否几近重合之外,也可以判断最后一次所构单纯形是否几近为一点,其收敛性判断的主体思想都是一样的,即判断最终构造点几乎为一点。
其改进复合形法的算法流程图如图4所示。
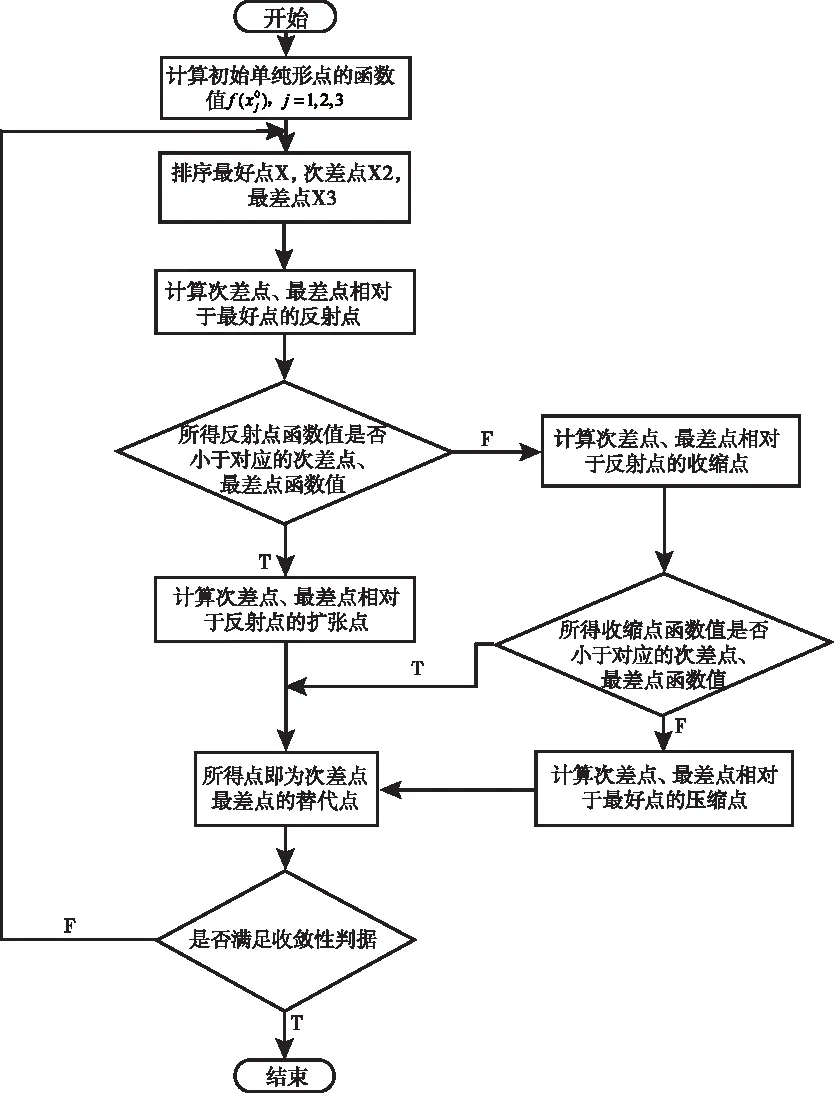
图4 改进算法程序框图
上述单纯形法的改进,省略了经典单纯形法中对于形心点的计算,同时对杨晋算法[9]单一方向的探索进行改进,在次差点与最好点、最差点与最好点两个方向进行计算和探索,以此求得新的单纯形探索构建点,省略了反射点与次差点的比较过程,算法简单,探索速度快。本文借用一个案例函数对改进算法和经典算法进行比较,验证改进算法的可行性。案例目标函数如式(6)所示,收敛性要求0.01。

(6)
两种方法单次单纯形最优值与迭代次数的关系对比图,如图(5)所示。
通过图5的对比分析,针对式(6)所示案例目标函数,改进算法在第3次迭代过程中,出现大幅度改变,从第6次迭代开始进入函数收敛区域,而经典算法在第13次迭代才有大幅度的转变,从第20次迭代开始进入函数收敛区域。改进算法的迭代速度相较于经典算法提高了58.33%,由此可得,改进算法的探索速度高于经典单纯形法,极大地提高了函数最优值求解的效率。

图5 经典算法与改进算法单次最优值对比
3 飞艇优化目标函数
以往的飞艇优化设计着重于阻力系数的优化,忽略其它设计因素,本文在进行多次设计优化分析后,针对飞艇初始优化阶段,保留阻力系数和体面比两个重要的设计因素。其中,阻力系数直接决定飞艇推进功率,进而影响能源供给;体面比是艇囊体积与面积的比值,决定着系统浮力的有效利用率[11],其目标函数数学模型如式(7)所示
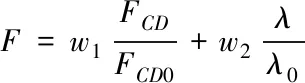
(7)
w1,w2为阻力和体面比的权重,FCD为阻力,FCD0为初始阻力,λ为体面比,λ0为初始体面比值。
3.1 阻力模型
Hoerner研究了流线型物体的阻力,对于多数飞艇,其艇体的气流是湍流[12],因此阻力系数关系如式(8)所示

(8)
其中l为艇体长度,d为艇体最大截面直径。
Hoerner提出对于实际水准的表面光洁度和Re>5×106,表皮摩擦系数Cf如式(9)所示

(9)
综合式(8),式(9),给出阻力系数公式,如式(10)所示

(10)
其中雷诺数计算参见式(11)

(11)
其中μ为粘性系数,ρa为气体密度,v为风速。
故阻力模型函数如式(12)所示
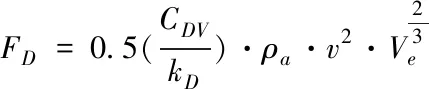
(12)
其中kD为整艇与裸艇之间的阻力系数比,由飞艇的实际构型决定,Ve为囊体体积。
3.2 体面比模型
针对飞艇初始化设计阶段,王全保[2]仅考虑表面积带来的影响,忽略优化过程中囊艇体积的变化,故此,本文引入体积模型,建立体面比影响模型,体面比模型可参照式(13)所示,式(14)-(15)为优化前期体积和表面积估算公式,其精确计算公式参照式(16)-(17)

(13)
其中囊体体积估算公式参照式(14)

(14)
对于飞艇优化初始阶段,艇体表面积估算公式,可参照式(15)
Se=(2.14+(l-60)·0.08-(d-15)·0.028×

(15)
其中体积精确值的计算公式参照式(16)

(16)
对于飞艇表面积精确值的计算公式,可参照式(17)

(17)
4 算例优化仿真分析
本文选取英国物理实验室所提出的一种低阻力飞艇形状,即后期Skyship飞艇形状的基础,NPL低阻力系数飞艇形状[12],作为飞艇前期优化的外形母线函数,其数学表达式如式(18)所示

(18)
l为飞艇长度,d为飞艇直径,其NPL低阻力系数飞艇外形如图6所示。

图6 NPL低阻力系数飞艇外形
本文参照雷诺数Re>5×106,以及实际飞艇设计案例,取初始飞艇长度60m,最大截面直径20m,长细比3。取飞艇高度为20km高空,大气压力5474.8Pa,风速25m/s,空气密度取0.088kg/m3,根据实际设计经验,以一定的最佳长细比范围为约束,此外考虑到飞艇的最大浮力,故以固定的囊体体积为约束,如式(19)所示
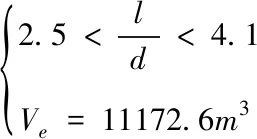
(19)
运用改进复合形法进行目标函数的优化探索,借用Matlab软件生成优化后的飞艇外形,如图6至图8所示,其中图6对应阻力权重为1,体面比权重为0,以此求得以阻力为优化重点时的优化艇形,图7对应阻力权重为0,体面比权重为1,以此求得以体面比为优化重点时的优化艇形,图8对应阻力权重为0.5,体面比权重0.5,以此求得阻力与体面比平衡时的优化艇形,需要指出的是,在实际设计优化工作过程中,设计者可以根据实际需求更改调配、本文只给出常用的几组权重分配比例,此外,也可以针对目标函数增添其它设计影响因素,本文保留两项随长细比变化呈现相反变化的阻力和体面比因素项。
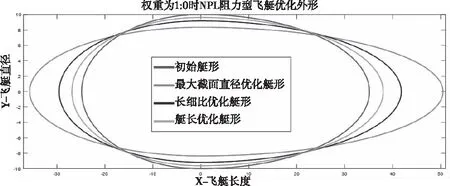
图7 权重为1:0时飞艇优化外形

图8 权重为0:1时飞艇优化外形
此外,根据所得优化值点,本文给出三个不同侧重点的优化结果,分别对应每组图中的除原始艇形外的三条优化曲线,若设计考虑目标函数值最优,则选择以优化点的最大直径为恒定值的优化结果,若设计考虑长细比的范围,则选择以优化点的长细比为恒定值的优化结果,若设计考虑飞艇的微小外形优化,则以优化点的艇长为恒定值的优化结果。
权重分配为阻力为1,体面比为0时的优化结果如图7所示。
从图7可以看出,当以阻力作为优化目标时,优化后的艇形会变细长,即整体艇体长度变长,最大截面直径变小,抗阻能力增强,其详细相关对比数值参见表1。

表1 权重为1:0时优化艇形与原始艇形对比
从表1中可以看出,当权重分配为1:0时,从三个侧重点优化所得艇形的阻力得到有效地改善,体面比则会相应的减小。
权重分配为阻力为0,体面比为1时的优化结果如图8所示。
从图8可以看出,在以体面比为优化目标时,优化后的艇形会变短胖,即整体艇体长度变短,最大截面直径变大,更有利于艇体浮力的利用,其详细相关对比数值参见表2。

表2 权重为0:1时优化艇形与原始艇形对比
从表2可以看出,当权重因子全部分配给体面比时,所得优化艇形的体面比得到显著提升,相应的截面变大,艇长变短,阻力会增大。
通过图7与图8的优化结果可以看出,体面比和阻力是优化过程中两个呈现相反增量的目标量,所以,在实际的优化过程中,还需要依照实际需求分配阻力与体面比的权重。
本文同时给出权重分配为1:1时的优化艇形结果,如图9,表3所示。
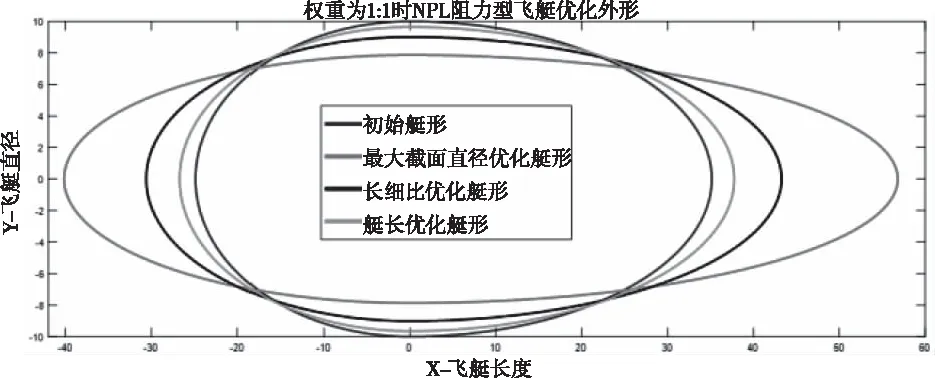
图9 权重为1:1时飞艇优化外形
从上述表1、2、3的仿真分析可以看出,优化过程中体面比与阻力呈现相反优化增量关系,故在实际应用中应根据实际需求分配权重因子,此外,本文考虑实际优化设计的三个关键变量,最大截面直径、长细比和飞艇长度,分别有侧重地提出优化方案,从优化结果来看,改进算法在飞艇优化中是可行的。
5 结论
本文结合传统飞艇优化设计过程中单一考虑阻力因素的问题,首先引入体面比,构建优化函数数学模型,构建优化流程框架,其次针对传统最优值求解的复合形法进行改进,依照双向同步探索思维,提出最优值求解的改进算法,并将其应用至飞艇外形优化设计中,运用Matlab进行函数的计算和仿真,通过仿真分析验证了算法的可行性。
