基于跃变量分析的航天器遥测数据可信度计算
2023-07-29张香燕李志强
张香燕,李志强,邱 瑞
(北京空间飞行器总体设计部,北京,100094)
1 引言
航天器遥测数据传输过程涉及多个环节,包括星上遥测采集、测控站数据接收、地面网络传输等,各个环节的不稳定因素均会导致遥测误码的产生。在航天器在轨运行管理中,航天器遥测数据是了解航天器系统运行状况的关键所在[1],如果遥测数据存在大量误码,将严重影响地面系统对航天器在轨运行状况的准确判断。因此,在遥测数据预处理中,检测、识别遥测数据的可信度,剔除相关误码,这对航天器在轨运行管理具有重要意义。
目前,遥测数据的处理方法一般采取数字滤波剔除异常值的方法,如卡尔曼滤波[2,3]、最小二乘法滤波[4]、基于小波变换的滤波[5-7]等,这些方法[8-15]可应用于遥测数据的分析与预报,但对于瞬时故障数据,其在轨特征表现为野值形式,往往会被数字滤波滤除,从而使地面系统无法及时获取航天器的突变故障,可能错失抢救航天器的最佳时机。
针对如何从航天器遥测数据中准确分离出航天器真实故障数据和误码的问题,本文提出了一种基于跃变量统计的遥测数据可信度分析方法,该方法将航天器的实时遥测数据与历史遥测数据关联起来,提取了遥测数据的跃变量统计特征数据,并建立了遥测数据的可信度计算模型,从而计算得到遥测数据的可信度,这对于航天器在轨故障诊断和数据分析具有重要的指导作用。
2 航天器遥测数据的跃变量统计方法
2.1 遥测数据变化规律
遥测数据可信度分析的基本原则是假定遥测数据的变化符合一定的规律。遥测数据的变化规律主要分为:恒定值、稳定变化、周期性变化、平缓波动、阶跃性变化、脉冲性变化、递增变化、递减变化。
对于恒定值、稳定变化、周期性变化、平缓波动、递增、递减的变化规律,现在一般通过区间过滤的方法有效剔除野值。而对于阶跃性变化或脉冲性变化,无法确认这个参数是否正常,但是如果出现的是方波(可以有一定误差),表示至少有连续两个值相同,则可以认为这几个参数的值都是可信的;或者孤立脉冲连续出现,则通过历史跃变统计这个数据也会表现为可信度比较高。因此,本文重点研究阶跃性变化或脉冲性变化遥测数据的剔野方法。
基于以上原则,利用统计学原理,从每一个历史遥测数据中提取特征数据,从特征数据中构建数据的历史统计规律,依据遥测数据特征值的统计规律可判定每一个新出现的实时遥测数据的可信度。这里的特征数据选择遥测数据的跃变量,即该遥测数据点与不同前驱点和后继点的差值。通过此方法可以分离出异常数据中的卫星故障数据与干扰数据,进而从异常数据中滤除干扰数据,基于此提出了基于跃变量的遥测数据可信度分析方法。
2.2 特征值提取
遥测数据特征值提取的输入是航天器相关参数在某一个时刻的遥测数据值。而判断数据的可信度的思想是比较该时刻参数遥测值与历史及未来该参数遥测值的相关关系来确定,因此遥测数据的跃变量成为一种主要的特征数据。下面分别定义两种方法的遥测数据特征值。
2.2.1 遥测数据与历史数据比较所得的跃变特征值
设t0时刻某参数的遥测数据值为y0,并且其对应的历史时刻t1,t2,t3,t4,t5的遥测值为y1,y2,y3,y4,y5,如图1所示。
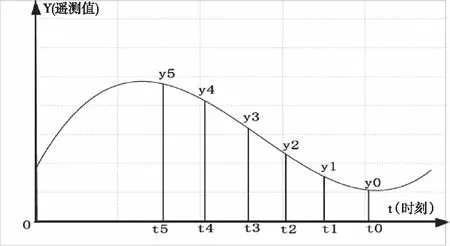
图1 遥测数据变化(1)
则t0时刻遥测数据y0的特征量由如下5个参数表示
Jumpi=|(y0-yi)/(t0-ti)|i=1,2,3,4,5
(1)
其中yi表示t0时刻遥测数据y0的前躯点,Jumpi为t0时刻遥测数据y0对应的特征数值,Δt=t0-t1为遥测数据采样时间的最小时间间隔。并且特征值的最小值MinJump为
MinJump=Min(Jump1,Jump2,Jump3,Jump4,Jump5)
(2)
2.2.2 遥测数据与历史未来数据比较所得的跃变特征值
设t2时刻某参数的遥测数据值为y2,并且其对应的历史时刻t0,t1,t3,t4的遥测值为y0,y1,y3,y4如图2。
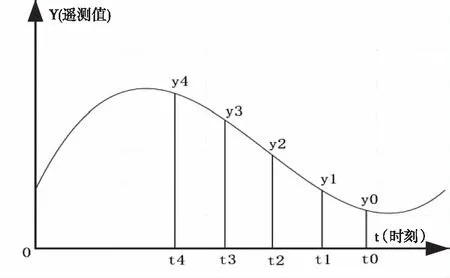
图2 遥测数据变化(2)
则t2时刻遥测数据y2的特征量由如下4个参数表示
Sumtm1=|(y1-y2)/(t1-t2)|
(3)
Sumtm2=|(y0-y2)/(t0-t2)|
(4)
Pretm1=|(y2-y3)/(t2-t3)|
(5)
Pretm2=|(y2-y4)/(t2-t4)|
(6)
其中y3、y4表示t2时刻遥测数据y2的前驱点,y1、y0表示t2时刻遥测数据y2的后续点。Sumtm1、Sumtm2、Pretm1、Pretm2为t2时刻遥测数据y2对应的特征数值,Δt=t2-t3为遥测数据采样时间的最小时间间隔。并且特征值的最小值MinJump为
MinJump=Min(sumtm1,sumtm2,pretm1,pretm2)
2.3 特征值统计规律分析
针对遥测数据特征量Jump1、Jump2、Jump3、Jump4、Jump5或Sumtm1、Sumtm2、Pretm1、Pretm2进行统计,统计出每个跃变值对应的跃变点的总数量。以某卫星为例,采用上述两种特征值提取方法,以遥测历史数据分别计算典型遥测数据的特征值统计规律,以温度类遥测数据为例进行了说明。
2.3.1 典型遥测数据特征值1统计规律
某温度类遥测数据特征量Jump1、Jump2、Jump3、Jump4、Jump5统计结果如图3至7所示(特征数据1统计结果,10天数据,总计1687350个遥测点,0.5%误码率,横坐标为跃变值,纵坐标为跃变点数量累积值)。

图3 特征数据Jump1统计结果

图4 特征数据Jump2统计结果

图5 特征数据Jump3统计结果

图6 特征数据Jump4统计结果

图7 特征数据Jump5统计结果
2.3.2 典型遥测数据特征值2统计规律
某温度类遥测数据特征量sumtm1、sumtm2的统计结果如图8所示,pretm1、pretm2统计结果如图9所示(特征数据2统计结果,10天数据,总计105410个遥测点,0.5%误码率,横坐标为跃变值,纵坐标为跃变点数量累计值)。
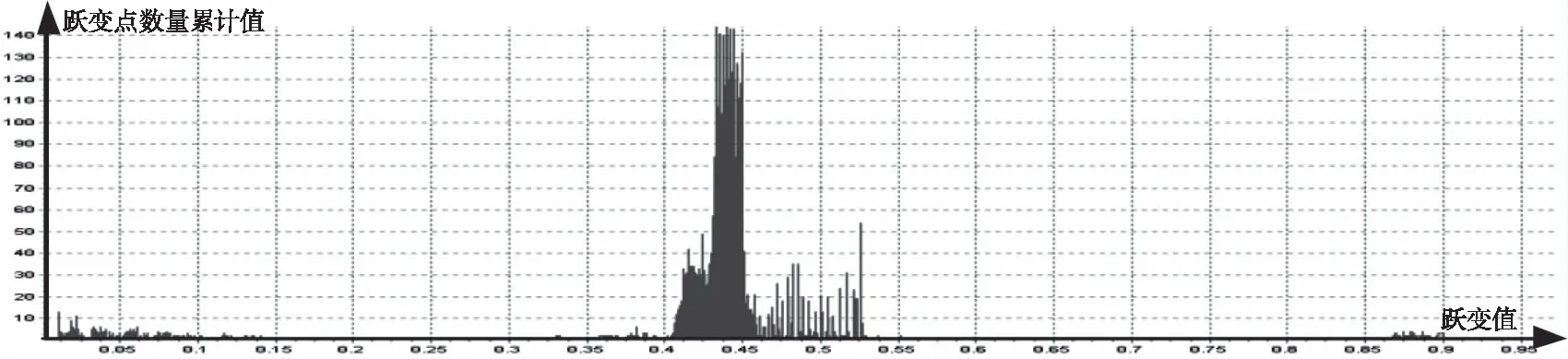
图8 相邻点特征数据统计结果
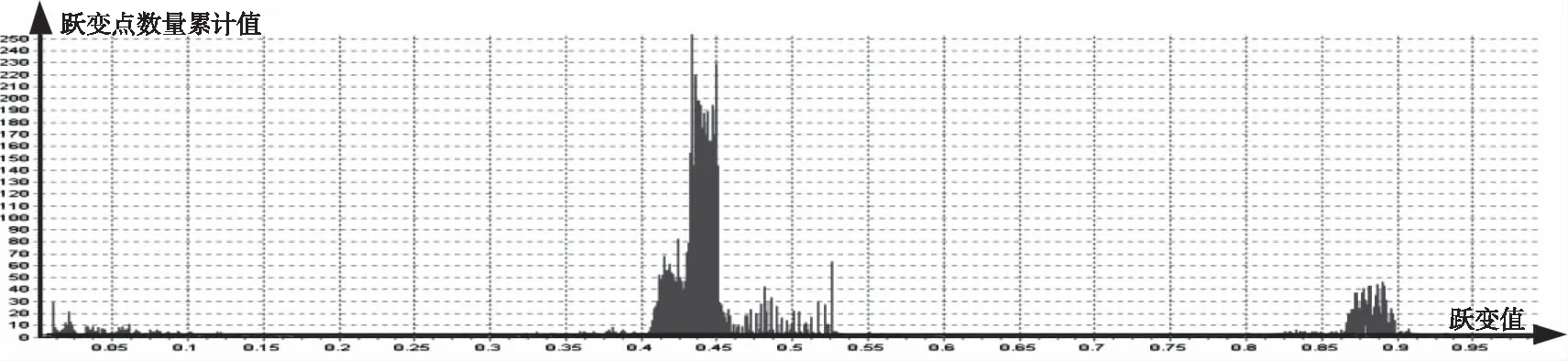
图9 相隔一个点特征数据统计结果
3 遥测数据的可信度计算
3.1 遥测数据可信度计算方法
将实时遥测数据的特征值与历史遥测数据特征值统计规律进行比较,计算出不同特征值统计规律下的可信度。遥测数据的可信度计算如下

(7)
其中,sum表示历史遥测数据的总数;sumcount表示跃变量统计区间[a,b]内所有历史遥测数据点出现次数的总和。
历史遥测数据的总数sum是已知的,而sumcount的值完全由区间[a,b]来决定。因此,为了计算某遥测数据点x的可信度,必须首先确定遥测点x的跃变量统计区间[a,b]。特征值的最小值MinJump为某遥测数据点x的特征值最小值,即表示某时刻的遥测数据点与前后时刻数据点的跃变量的最小值,代表了此时刻遥测数据与前后数据的最好一致性情况。为了确定某遥测数据点x对应的统计期间,以MinJump(x)为中心点,以Jspan(x)为统计区间[a,b]的一半长度,即某遥测数据点x的跃变量统计区间[a,b]由下式给出:
a=MinJump(x)-Jspan(x)
(8)
b=MinJump(x)+Jspan(x)
(9)
Jspan(x)=MinJump(x)*10%+Span
(10)
其中,MinJump(x)为当前遥测点x特征数据中的最小值;Span为模糊系数。
3.2 模糊系数的确定
遥测数据可信度分析的效果需设计相应的指标进行考核,从而确定模糊系数span。遥测数据的可信度分析效果指数主要体现在对遥测数据误码的误判和漏判上,一般用误判遥测点数和漏判遥测点数的总和除以判决总遥测点数来表示。可信度分析效果指数越小,说明误码剔除的效果越好。但是,为了避免误判,应尽量使误判点数越少越好,因此,将误判遥测点数的加权系数翻倍,可信度分析效果指数设计为
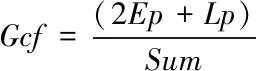
(11)
其中,Ep表示误判遥测点数,Lp表示漏判遥测点数,Sum表示判决总遥测点数。在遥测数据处理中,可信度分析效果指数越小越好。
对于不同的模糊系数Span值,计算得到其对应的可信度分析效果指数Gcf。为寻找span与可信度分析效果指数间的关系,对某卫星的典型温度值实际数据进行了计算。为放大模糊系数Span<1时的可信度分析效果指数的变化情况,将模糊系数Span取自然对数做自变量,可信度分析效果指数Gcf做因变量,得到Gcf与Ln(Span)间的散列点分布情况。并通过对散列点分布进行二阶多项式拟合,结果如图10所示。

图10 某温度遥测Ln(Span)与Gcf的拟合曲线
针对多类型遥测数据进行了分析,一般情况下,模糊系数与可信度分析效果指数的拟合曲线均满足二次多项式关系曲线,具体如图11所示。

图11 某电压、状态遥测Ln(Span)与Gcf的拟合曲线
因此,可信度分析效果指数可以近似的表示为模糊系数的二次多项式
Gcf(x)=ax2+bx+c
(12)
其中,x=Ln(Span)。
为了使可信度分析效果指数Gcf达到最小值,也就是使遥测数据中误判和漏判总数达到最少,则有下式成立
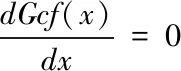
(13)
可得

(14)
即

(15)
因此,可确定最佳模糊系数为
Span=e(-b/2a)
(16)
所以,通过对拟合出的多项式求极值的方法,可以精确地获得某遥测参数最佳模糊系数值。
3.3 可信度系数计算
根据遥测数据可信度R得到遥测数据点的可信度系数Ni。可信度系数Ni的计算公式如下
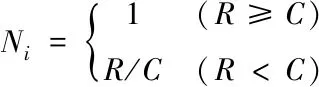
(17)
其中,C为分割点可信度临界值。
下面具体介绍分割点可信度临界值C的选择。选取不同的E点分割线时可信度分析效果指数的变化情况如下图12所示。
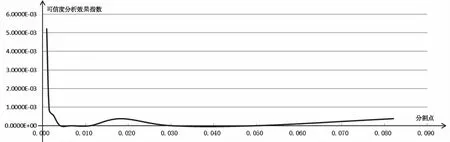
图12 分割点临界值C与可信度分析效果指数Gcf的关系图
由此得出结论:
1)分割点在0.004~0.06范围内选取时,对可信度分析效果几乎没有影响。
2)当分割点小于0.004时,会使可信度分析效果急速劣化。
3)当分割点大于0.06时,对可信度分析效果有一些影响且有变大的趋势。
根据试验中的计算结果,一般选取0.01为默认分割点,即一般选取C=0.01。
4 仿真验证
航天器在轨遥测数据的可信度计算主要根据遥测数据的特点,通过大量的遥测数据统计检验,抽象出遥测数据可信度检测模型。由于原始遥测数据观察,误码率极低,为了更好地验证基于跃变量的遥测数据可信度分析方法,进一步检验可信度计算模型的适用性,对真实的遥测数据人为加入一定量的误码数据,有两个方面的好处:一是可以准确定位误码数据的出现点,二是可以验证遥测值可信度计算模型的适用性。
以某卫星的温度遥测值可信度计算为例进行仿真验证。遥测数据误码加入的方法如下:①以某星10天的温度遥测值为学习数据,为获得特征值统计规律,学习数据的误码数据人为加入方法为:数据误码率为0.5%且随机选取,误码数据幅值范围为-10000~+10000且随机选取。②验证数据的选取:以某星1天的温度遥测值为基础数据,并人为加入一定量的误码数据,加入方法为:数据误码率为0.5%且随机选取,增加连续20分钟、20%误码率的误码,误码数据幅值范围为-200~+200且随机选取,增加误码后的验证数据如图13所示;(注:为获得可观测的结果,幅值范围进行了压缩,否则,原始遥测数据将被误码淹没,可观测效果极差)。

图13 增加误码后的验证数据
航天器在轨遥测数据的可信度计算的具体步骤如下:
1)统计历史遥测数据中特征值的规律。针对增加误码后的学习数据,根据1.2.1节方法二,计算得到遥测数据与历史未来数据比较所得的跃变特征值统计特性。
2)实时遥测点特征值提取。针对增加误码后的验证数据实时遥测数据点,根据1.2.1节方法二,计算该遥测点的特征值,并求解得到Minjump。
3)确定该遥测点统计区间[a,b]。根据学习数据,利用2.2节可信度分析效果指数最小化的方法,确定出最佳模糊系数span,根据2.1节式(8)、(9)、(10)可以确定出实时遥测数据点的跃变量统计区间[a,b]。
4)计算遥测数据的可信度。根据式(7)可以计算出实时遥测数据点的可信度R。
5)计算遥测数据可信度系数。根据式(17)可以计算出实时遥测数据点的可信度系数Ni,一般取分割点为0.01,当Ni≥0.01时,则认为遥测数据可信。针对每个时刻的验证数据,按照步骤2)~5)进行可信度计算。
6)获得平滑后的遥测数据。当计算出的某遥测数据为不可信数据时,以该点前一时刻的可信遥测数据替代所检测出的不可信遥测数据,从而对验证数据进行平滑。平滑后得到的遥测数据结果如图14所示。
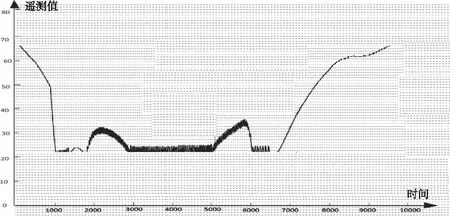
图14 经可信度计算平滑后的遥测数据
对比图13与图14,可以清晰地看出,该遥测数据可信度计算方法大大提升了处理后遥测数据的质量,减少了遥测误码,可以满足航天器实时遥测数据的可信度计算要求。
5 总结
本文通过对不同类型遥测数据的在轨变化规律分析,提出了一种基于跃变量统计的遥测数据可信度分析方法。该方法利用统计学原理,从每一个历史遥测数据中提取跃变量特征数据,从而分析出特征数据的历史统计规律。在此基础上,建立了遥测数据的可信度计算模型,从而依据遥测数据特征值的历史统计规律可计算出每一个新出现的实时遥测数据的可信度。最后利用仿真验证了该可信度计算方法的可行性和有效性。
