基于改进PD的LESO四旋翼控制算法
2023-07-29刘春玲冯锦龙
刘春玲,冯锦龙,张 瑾
(大连大学信息工程学院,辽宁 大连 116622)
1 引言
四旋翼飞行器控制系统是一个非线性、强耦合的复杂系统,给控制设计带来了巨大的挑战,针对这一复杂系统,文献[1,2]用经典PID设计控制器,因实现简单、有良好的抗干扰能力等,在四旋翼飞行器控制系统的设计中得到广泛应用,然而其处理耦合问题的能力较差及不能自适应调整参数。文献[3,4]设计了改进型PID控制器,利用在经典PID控制原理基础上进行了改进,但未考虑飞行环境中的未知扰动[3]和需要精确的数学模型[4]。文献[5-7]设计了双回路PD参数优化控制器,该设计通用性强、易实现,寻优速度快且跟踪效果良好,然而在四旋翼飞行器建模过程中,忽略了空气阻力和未知扰动等。文献[8,9]设计了PID的滤波器控制器,该方法能实现良好的鲁棒性,但对强耦合的非线性四旋翼控制系统控制不理想。文献[10,11]采用模糊PID控制器,该方法有良好的动态性能,但需要更细化的模糊规则,增加了该方法的实现难度。
针对四旋翼非线性、强耦合及易受外界干扰引起姿态不稳定问题,设计了基于改进型PD的LESO(Liner Extended State Observer)飞行控制方法。首先,在反馈回路中设计了LESO,运用LESO原理实现四旋翼姿态的解耦控制,同时对系统的内外部扰动进行估计补偿到原系统中,增强系统鲁棒性;然后利用改进PD控制,增强系统动态特性,降低外界信号对飞行控制系统的干扰,提高系统的抗干扰能力。
2 四旋翼飞行器数学模型
在四旋翼建模时,假设机体是质量均匀且对称的刚体,四个旋翼为刚性且不会发生形变,机体坐标和质心坐标重合。
四旋翼飞行器的结构如图1所示,Mi代表各个旋翼的电机,定义惯性坐标E(XYZ)和机体坐标B(xyz)之间的相对位置可以通过位置坐标确定,飞行器在地面坐标系下的姿态角θ,φ,ψ为机体坐标系下的pitch,roll,yaw,即俯仰角、滚转角和偏航角,令R(θ,φ,ψ)表示惯性坐标E和机体坐标B之间的转换矩阵,可以表示为
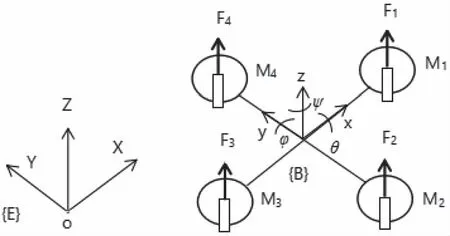
图1 四旋翼飞行器坐标及电机示意图
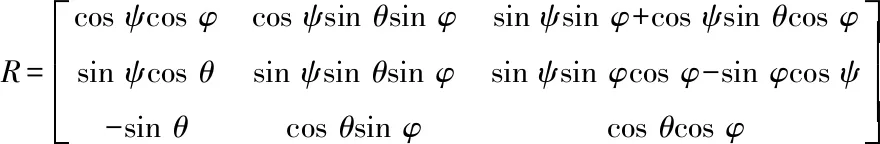
(1)
四旋翼飞行器非线性运动方程分为平移运动和旋转运动。由牛顿第二定律得x,y,z方向的平移运动表示为
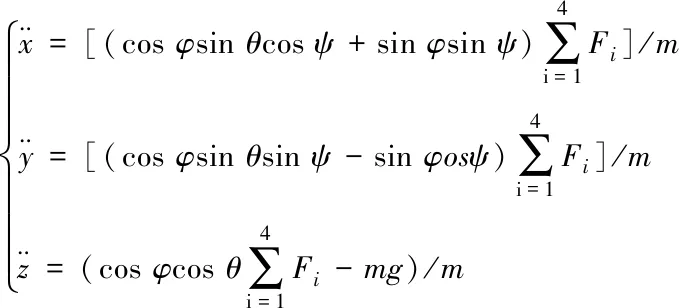
(2)
其中Fi(i=1,2,3,4)为螺旋桨的升力,m为四旋翼机体的质量。
根据角动量守恒得四旋翼旋转运动的表示为
其中Ii(i=x,y,z)为轴的转动惯量,l为机体轴心距,Di(i=θ,φ,ψ)为环境中不确定的干扰分解到坐标轴的分量。
为了简化四旋翼的平移运动和旋转运动,定义虚拟控制量U1,U2,U3,U4为四个独立的输入,分别以升力F1,F2,F3,F4进行变换,变换公式可表示为
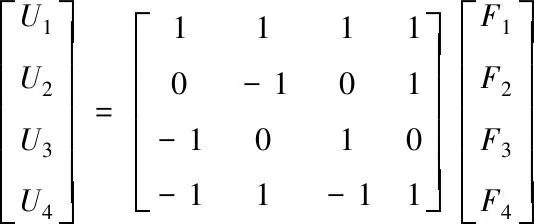
(4)
结合方程式(2)、(3)和(4),四旋翼无人机飞行器系统的动力学模型可表示为:

(5)
3 改进型PD的LESO控制器设计
3.1 改进型PD
常规PD控制器通过对比例系数和微分时间常数的适当调整,可达到较为良好的控制效果,其结构如图2所示。
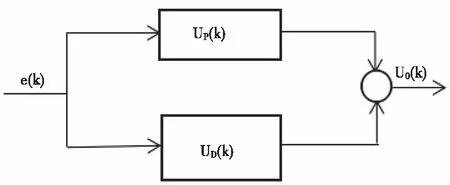
图2 常规PD控制器
PD控制器的控制规律表达式可表示为

(6)
式中kP为比例系数,TD为微分时间常数,e(k)为系统误差。
对PD控制器的微分项可表示为
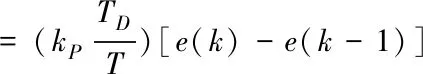
(7)
由式(7)可以看出,微分环节的引入,改善了系统的动态特性,但对高频干扰信号特别敏感,容易引入扰动。同时说明在误差扰动突变时会显出微分项的不足,而且长时间系统会积累静态误差,导致鲁棒性下降,很难达到预期的控制效果。
为克服上述问题,在常规PD算法中加入了一阶惯性环节Df=1/(1+Tf(s)),则改进型PD控制器,结构如图3所示。

图3 改进型PD控制器
改进型PD控制器的控制规律可表示为
u0(k)=uP(k)+uD(k)+uDf(k)
(8)
式中uP(k)为比例控制,uD(k)加上uDf(k)为微分控制,e(k)为系统误差。
对于微分环节加入一阶惯性后,其微分方程形式可表示为

(9)
将(9)式离散化,可表示为:
(10)
式中Tf为一阶惯性常数,T为采样周期。
对(10)式整理有:
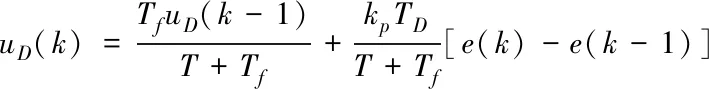
(11)
对(8)~(11)式进行整理可得:
u0(k)=kpe(k)+uD(k)+uDf(k)=kpe(k)+kd(1-α)[e(k)-e(k-1)]+αud(k-1)
(12)
由数学模型知,四旋翼的旋转运动方程是一个多输入多输出非线性耦合系统,此处利用线性自抗扰控制算法中的线性扩张状态观测器对系统耦合部分及外部扰动进行实时跟踪和估计,并结合系统控制律将估计值进行补偿并反馈到原系统中,不仅将多输入多输出的非线性耦合系统转变成相对独立的单输入单输出线性子系统;还可以通过LESO有效的剔除系统内外部扰动,减少反馈误差,增强系统抗外部干扰能力和对自身参数不确定等因素的适应能力,改进型PD的LESO控制器框图如图4所示。
3.2 线性扩张状态观测器
线性扩张状态观测器[12,13]是线性自抗干扰的核心组成部分,其工作原理就是把系统中的各种干扰扩张为一个新的状态变量,通过系统控制律和输出动态的估计总扰动,并有效对总扰动项进行反馈补偿到原系统中,不仅能解决四旋翼模型不确定部分引起的内部干扰,还能增强控制系统的鲁棒性。
以滚动通道φ为例,详细描述建立四旋翼飞行器单输入单输出的线性扩张状态观测器的二阶数学模型,有

(13)


(14)
然后对系统(14)的LESO进行如下设计
(15)
由(15)式可知,LESO通过适当的观测器参数[β1,β2,β3]=[3w1,3w2,w3]T来估计状态变量x1,x2和扩展状态变量x3,即各个状态X=(x1,x2,x3)对应估计值Z=(z1,z2,z3),其中w为观测器带宽,利用LESO将控制系统中的内外部扰动进行估计并补偿到原系统中,不仅能减少系统误差,根据文献[14]可知,只需保证w的取值大于零且总和扰动有界便可以保证LESO的稳定性。
为有效剔除四旋翼飞行控制系统中的扰动,其控制率可设计为

(16)
以四旋翼动力学数学模型中翻滚通道为例说明,取方程式(5)做如下变化。

(17)

(18)
式中b0=l/Ix,u=u2。
根据式(17)、(18)处理后,对象的状态方程可以写作如(19)所示。

(19)
式中x1=φ,u=u2,由式(19)知,原非线性系统(13)已转化为线性系统(19),且系统中不确定扰动被实时动态线性化。基于改进PD的LESO控制算法设计步骤如下:
(i) 通过欧拉方程和角动量守恒建立四旋翼的非线性数学模型,选取对象模型的非线性、耦合及未知部分作为扰动项并建立如式所示的“动态线性化”模型。
(ii) 根据线性化模型,设计改进型PD控制器的控制率u0。
(iii) 选取合适的β1,β2,β3,使LESO能对总扰动项z3更好的估计,并动态补偿到原系统中,改进型PD控制器输出u0,得到实时控制量u=uo-z3/b0。
4 仿真结果及分析
为验证所提出的算法有效性,采用Matlab进行四旋翼飞行器控制系统的仿真。四旋翼飞行器物理参数如表1所示,仿真参数如表2所示。

表1 四旋翼飞行器物理参数
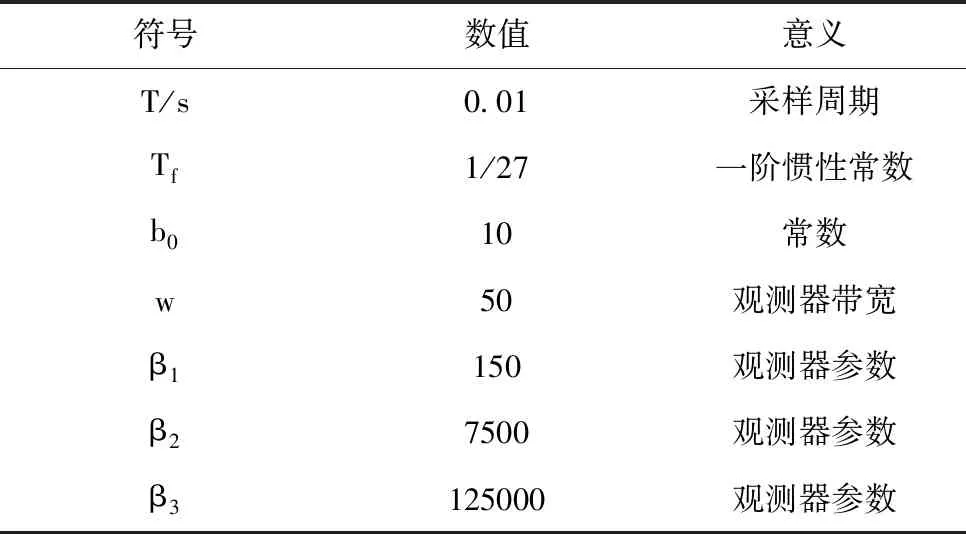
表2 仿真参数
4.1 姿态及轨迹分析
仿真时,为模拟四旋翼飞行过程中环境扰动不确定及飞行轨迹,设定四旋翼飞行器飞行轨迹路线沿(3,2,0)到(0,0,5),在沿轨迹飞行过程中给翻滚角加入扰动,模拟四旋翼器飞行环时的内外扰动,并将扰动设置为0.5(sign(sin(0.5t))+cos(0.6t)+cos(0.7t)+0.5sign(sin(t))),且在3s时加入扰动,仿真如下。
由图5和图6可知,在3s时给翻滚角加入扰动后,PID控制仿真图翻滚通道位置的幅值是改进PD的LESO控制器的幅值的1.6倍,且前者幅值跳变较为陡峭,后者较为平缓;除此之外,由PID控制和改进PD的LESO控制器的俯仰角对比知,后者调节时间较短;由PID控制和改进PD的LESO控制器的偏航角对比知,后者不仅调节时间较短,而且幅值调节也较为平滑。由对比可知,在四旋翼飞行器飞行中受干扰时,改进PD的LESO控制器对位置的调节能力优于经典的PID控制器。

图5 PID位置调节
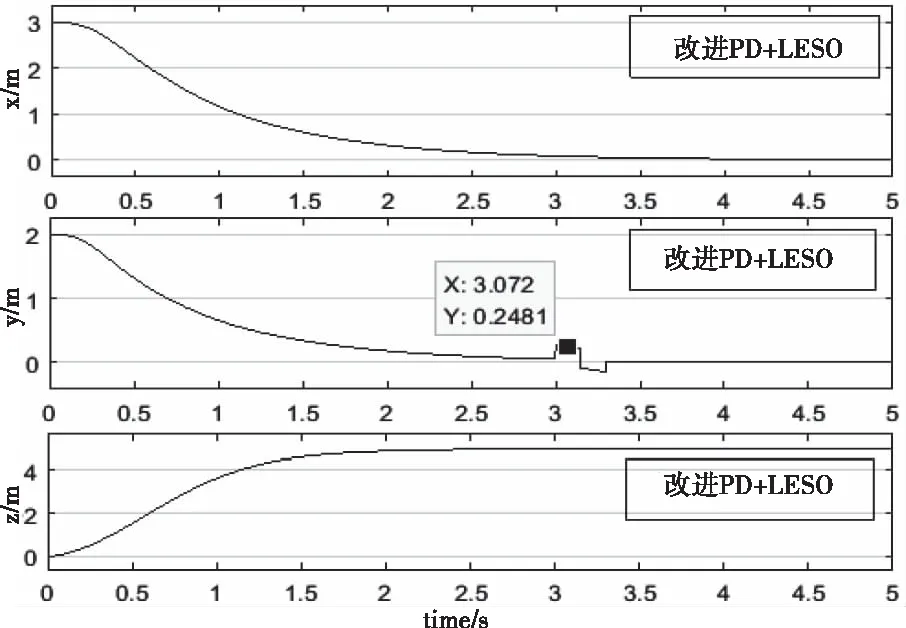
图6 改进PD的LESO位置调节
由图7和图8可以看出在3s时加入扰动后,PID控制仿真图翻滚通道的姿态调节幅值为0.057rad,受到干扰后调节趋势较为陡峭;俯仰角调节较为平缓,但调节幅值较大;偏航角调节时间为2.5s左右。改进PD的LESO控制器翻滚通道姿态受干扰后调节幅值约为PID控制器的一半,且受到干扰后调节趋势较为平缓;俯仰角调节较为平缓,且调节幅值远小于PID控制的俯仰角调节幅值;偏航角调节时间为0.5s左右,响应时间远小于PID。除此之外,PID控制翻滚角姿态的幅值为0.28rad左右,且较为陡峭;俯仰角在达到平稳前幅值0.4rad左右。改进PD的LESO控制器翻滚角姿态幅值为0.18rad左右,且较为平缓;俯仰角在达到平稳前幅值为0.25rad左右。可见改进PD控制器结合LESO对扰动进行补偿后,能够明显提高各通道的姿态角解算能力,减少幅值跳变。仿真结果表明,所设计的控制器,可以明显提高四旋翼旋转运动的抗干扰能力,增强系统的鲁棒性。

图7 PID姿态调节

图8 改进PD的LESO姿态调节
5 结论
针对四旋翼飞行器非线性、强耦合和易受外界干扰引起姿态不稳定问题,设计了一种改进PD的线性扩张状态观测器(LESO)控制器,并以经典PID作为参考。仿真结果表明,通过改进型PD控制器,利用LESO原理对扰动估计并补偿到原系统中,不仅能够有效抑制系统误差,还能增强控制系统的抗干扰能力和鲁棒性,且具超调量小和控制效果更佳。该控制方法在四旋翼飞行控制领域有着可待的应用前景。此外,进行了对比仿真,表明该控制器实现了令人满意的跟踪精度和更优越的控制性能。希望未来通过实际的四旋翼无人机飞行实验验证所提出控制器的有效性。
