基于HDLMD 和JRD 距离的电机轴承故障信号分解及性能评估

刘 超

（华中科技大学 同济医学院附属梨园医院，武汉 430077）

目前，轴承已成为旋转机械设备的一项关键部件，该部件的性能对设备整体控制精度与运行可靠性发挥着重要作用，如果未采取有效监测措施提前判断故障问题，将会造成机械设备在运行阶段出现明显波动的情况，从而导致较大经济损失甚至造成人员伤亡的严重后果[1-2]。由此可见，如何准确评价轴承性能退化程度已经成为一项非常重要的研究课题。

但当轴承中存在故障问题时则会形成非线性变化的振动信号，表现出明显波动特点，同时形成了模糊故障特征，导致轴承性能退化评估难度显著增大。因此进行设备监控管理过程中还需进一步构建更加简单、高效的轴承性能评价技术[3-4]。对信号分量进行筛选的结果准确性直接影响到后续特征提取的效果，这也成为信号分解的一个核心因素。到目前为止，学者们已经开发出了峭度、相关系数等多种类型的筛选规则，但如果只根据以上两项指标进行筛选时则会造成结果产生明显偏差以及无法准确区分指标数值的缺陷[5]。LS 属于一类无监督特征选择技术，可以根据局部信息控制性能与分值效果选择合适的特征参数[6]，确保故障参数特征中的几何数据指标得以充分保留，对于图像信息分析研究等方面都发挥着重要作用，可以通过上述方法完成特征筛选，从而获得对故障轴承特征敏感度更高的分量。文献[7]根据LS 方法确定了完全集成经验模态分解方法（CEEMD）进行分解得到的固有模态函数（IMF）分量；文献[8]中以LS 方法实现特征降维，对故障分类性能起到了良好改善作用。根据以上研究结果，为防止设置过多特征分量维数使得信息冗余，并造成过长运算时间的问题，本研究利用拉普拉斯分值的方法分解HDLMD 获得PF 分量，再根据各参数重要性实施排序，以此确定含有最多故障信息的PF 分量。

还可以将特征提取和状态识别理解成一个持续的处理过程，但需要设置合适的性能评价指标[9]。针对上述情况，有学者提出了JS 距离的评价方法，但在评价期间都没有克服非对称、较大波动性以及信号识别能力差的缺陷，从而制约了实际工业领域的大规模推广应用。Renyi 熵属于一种在信息熵基础上进行扩展所得的结果，由此完成数据不确定性的准确分析[10]。JRD 距离是根据JSD 与Renyi 熵设计的一种能够对概率分布相似度进行定量评价的方法[11]，能够满足对称性、非负性、连续性与有界的多项要求，对各状态振动信号差异性进行了评价，有效克服了传统性能评估指标波动性大的缺陷[12]。

根据以上分析，本文采用HDLMD 与JRD 距离分析方法相结合的方式，设计得到了一种以HDLMD与JRD 实现的轴承性能测试方案，充分消除了DLMD中微分处理次数缺少理论依据的问题，构建形成了更完善的DLMD 理论分析系统。在上述研究基础上并根据JRD 距离，设计了轴承性能退化评价系统。通过测试CWRU 轴承实验与NASA 全寿命周期实验表明该方法满足可靠性与评价精度要求。

1 振动信号的HDLMD 分解

LMD 可以把初始信号自适应分解成经过调幅调频后的PF 分量，按照文献[6]的方法进行分解计算。先利用DLMD 算法完成信号的k 次微分处理后再对其实施LMD 分解，再对分解后的分量实施k次积分与一阶LMD 处理获得m 个PF 分量。利用微分方法调整信号中的各频率成分比例，由此提高信号中微弱高频成分的强度或对相近频率信号进行准确区分，能够充分消除LMD 模态混叠的情况。但到目前为止，尚未建立一种DLMD 微分次数的统一分析方法，本文根据前期文献报道开发了一种可以对微分次数进行有效计算的HDLMD 方法，其是利用Hilbert 解调的方式设置DLMD 中微分次数k，具体步骤如下：

（1）对待分解信号x（t）实施一次微分计算获得微分后信号x1（t）；

（2）再对信号x1（t）LMD 分解计算获得m 个PF分量；

（3）对PF 分量Hilbert 解调计算后，再通过Hilbert谱判断PF 分量是否出现频率混叠的情况；

（4）当遇到频率混叠的情况时，继续微分处理一次微分后的信号x1（t），获得经过k 次微分的信号xk（t）的LMD 未发生频率混叠的结果，将此k 作为DLMD分解的微分次数。

利用HDLMD 计算信号的k 阶微分，经过微分处理的信号频率保持不变，而分解后的信号能量则呈现持续降低的趋势，经过微分处理后则可以保留微弱高频信号与更高能量的频率信号。

2 JRD 距离方法

2.1 Renyi 熵

Shannon 熵属于一种对信号信息概率进行评价的方法，可以准确反馈设备运行状态。构建长度为M 的离散序列集合Y，确定概率为P，由此得到Shannon 熵表达式如下：

而Shannon 熵几乎不受数据末段变化的影响，难以识别初始信号中的轴承状态差异。因此设定以下Renyi 熵计算式：

由于Renyi 熵包含了α，对于随机序列可以更灵活评价，充分满足一般性。α→0 代表Renyi 具备更强熵感知端点变化性能；α→1 表示Shannon 熵，难以获取端点变化数据。上述结果表明，Renyi 熵可以满足大多数随机序列的分析需求。

2.2 JRD 距离

JRD 是根据JSD 以及Renyi 熵的方法评价概率分布相似度，JSD 距离则是以KLD 作为基础。当JRD距离越小时，说明2 个序列具备更相近的概率分布结果。将2 个随机序列概率分布依次表示成p（i）与p′（i），得到KLD 距离与JSD 距离如下：

式中：m（i）表示p（i）与p′（i）平均概率分布。对式（5）进行转化得：

当轴承保持良好运行状态时，PH 与PN 间基本一致，JRD 约为0；当轴承出现故障问题时，2 个分布的JRD 出现增加的现象，导致轴承故障也明显增加，产生了更明显的退化。

3 轴承性能评估方法

对轴承性能进行评价，具体流程如下：

（1）把轴承振动信号分成训练样本与测试样本两种类型，依次经过HDLMD 分解计算获得不同故障特征的PF 分量；

（2）从PF 分量中提取出时域特征参数并以此构成特征向量；

（3）通过以上特征向量集计算出PF 分量LS，当LS 越小时，说明故障信息量越多，完成分值排序后，去除LS 超过设定阈值的分量，以LS 低于设定阈值的分量构成有效分量；

（4）计算第（3）步中采集的有效PF 分量并计算概率分布结果，根据概率分布结果获得正常样本和测试信号Renyi 熵；

（5）通过Renyi 熵值计算测试信号和正常样本数据的JRD 距离，实现轴承退化性能的综合判断。

4 实验结果分析

4.1 数据分析

本文设计了一种对轴承进行退化状态识别的方法，并验证了该方法可靠性与合理性。本次选择的测试数据由美国CWRU 轴承数据库提供，构建得到的实验台如图1 所示。为驱动端配备了SKF6205 轴承，设定采样频率为12 kHz，转速为1750 r/min，将内圈故障裂纹尺寸依次设定在0.1761 mm、0.3542 mm、0.5123 mm，各类故障依次含有10 个样本，前5 个属于正常样本，各样本都由4096 个数据点组成。

如图2 所示，给出了轴承处于正常状态与内圈受到损伤依次为0.17 mm、0.36 mm 与0.54 mm 退化状态下对应的信号的时域波形。对图2 进行分析可知，轴承振动信号在各故障状态下形成的时域特征也存在较大差异，并且轴承处于正常状态下的振动信号幅度相对故障状态下的振动信号幅度更小。轴承未出现故障时，振动信号呈现无规律的特点，受到多种外部因素的干扰；当轴承中存在故障时，故障程度逐渐增大时，信号产生的冲击程度也越大，受到外部因素振动影响时，振动幅值也明显提高。

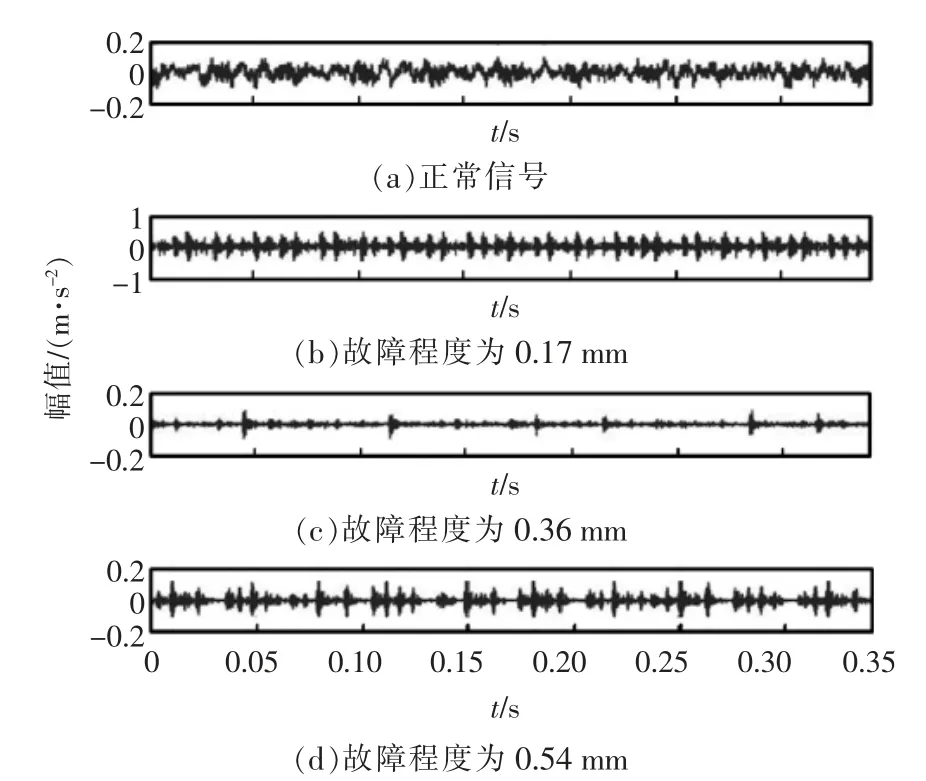
图2 轴承不同退化状态下信号时域波形Fig.2 Bearing signal time-domain waveform under different degradation states

按照本文设计的状态识别方式，对轴承的内圈故障实施HDLMD 分解计算。经过拉普拉斯分值处理后获得PF 分量信号，从PF 分量中提取获得6 个时域特征值，各样本分别构建5×6 特征值矩阵，计算该矩阵的LS，得到的结果如表1 所示。

表1 各PF 分量的拉普拉斯分值Tab.1 Laplace scores of each PF component

4.2 NASA 数据实验分析

本次选择的数据来自NASA 提供的IMS 轴承加速寿命，属于全寿命数据，是由初始健康状态过渡到轴承损坏的过程。对一个轴共配备了4 个ZA-2115 双列轴承。轴承各排分别包含16 个滚子，其中，螺距直径为7.15 cm，滚筒直径为0.84 cm，圆锥接触角为15.171°。各轴承座分别配备了PCB353石英ICPs 加速度测试仪，可以实现加速度数据准确采集。之后为各轴承外圈安装4 个热电偶。按照20 min 间隔条件进行振动数据采集。保持采样率为20 kHz，共获得20480 个数据点，控制驱动电机转速为2000 r/min。

NASA 全寿命周期波形如图3 所示。可知，轴承的第722 组数据产生了突变幅值，表明此时信号受到强烈冲击，可以推断轴承存在故障问题；到达972组数据时，幅值发生了大幅波动，轴承进入完全失效的阶段，到达985 组数据时发生完全失效，而在722 组前是否存在故障则无法判断。

图3 全寿命周期数据波形图Fig.3 Waveform of life cycle data

针对全寿命周期计算JRD 距离，提高不同退化状态差异性，结果如图4 所示。

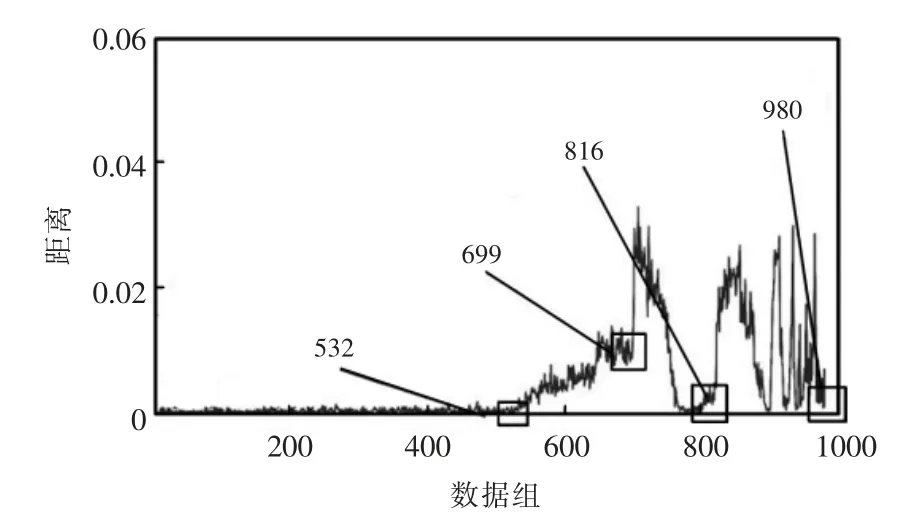
图4 HDLMD 分解JRD 距离Fig.4 HDLMD decomposition JRD distance diagram

分析图4 结果如下：

1）第1 组至532 组数据都呈现较小的JRD 距离，已经到达0 附近，也没有发生明显的波动，可以推断此时轴承保持正常运行状态；

2）到达第533 组数据时，JRD 距离开始持续提高，这是由于此时发生较大程度磨损而增大了振动程度，可以推断此时轴承进入了初始故障阶段；

3）JRD 距离在699 组数据下出现快速增大，之后逐渐降低至0，这可能是由于磨损后形成平滑表面的原因；

4）到达第816 组数据时，JRD 距离重新进入增大的阶段，之后JRD 距离发生剧烈波动，到达第980组样本时，发生了JRD 距离的快速升高，表明轴承已经进入失效的阶段；最终到达985 组数据时发生轴承的完全失效。

依次计算HDLMD 与LMD 分解得到的JRD 距离及方差值，结果如表2 所示。

表2 HDLMD 和LMD 分解的JRD 方差对比Tab.2 Comparison of JRD variance between HDLMD and LMD decomposition

根据表2 可知，以HDLMD 分解获得的JRD 距离方差相对LMD 分解的JRD 距离方差发生明显降低，表明HDLMD 分解得到的JRD 距离具备更小波动程度。

以上测试结果表明，采用本文设计的HDLMD与JRD 相结合的方法可以实现状态的精确识别。

根据上述轴承测试结果可知，本文构建的轴承性能评价方法同时融合了HDLMD 与JRD 距离的综合优势，先通过HDLMD 分解过程的微分方法调整初始信号中各频率成分比例；之后通过LS 充分保留故障信号的特征几何信息，由此确定故障信息的PF 分量；最后通过Renyi 熵准确评价振动信号处于各个退化状态的复杂性，由此完成轴承性能退化的分析功能。

5 结语

开展基于HDLMD 和JRD 距离的电机轴承故障信号分解及性能评估，研究得到如下有益结果：当轴承中存在故障时，故障程度逐渐增大时，信号产生的冲击程度也越大。NASA 全寿命周期波形表明此时信号受到强烈冲击，到达972 组数据时，幅值大幅波动，到达985 时发生完全失效。HDLMD 分解得到的JRD 距离具备更小波动程度，表明采用本文设计HDLMD 与JRD 相结合方法可以实现状态的精确识别。