随钻声波遥测数据还原质量的数值模拟分析

王 伟，闫向宏，周建航，刘钰姣

（1.中国石油大学（华东）理学院，青岛 266580；2.中国石油大学（北京）克拉玛依校区 文理学院，克拉玛依 834000）

随着勘探开发的不断深入，常规油气资源增储增产越发困难，而经济社会发展对石油与天然气能源的需求却不断增大，故而页岩油气及深层致密油气等非常规油气资源的大力开发已是大势所趋[1]。非常规油气资源储量十分丰富，但因储层地质结构极为复杂，勘探开发难度极大，钻井工艺要求也更为严苛，所以钻进过程中，及时掌握井底压力、井眼轨迹等井下工程参数及储层物性等地质参数极为重要，这是保障钻井安全、提高钻探效率及降低钻井成本的必然要求[2-5]，随钻测井技术正是满足这一要求的最佳选择。然而，钻进过程中钻柱基本处于旋转状态[6]，这使得通过有线方式实时获取井下测量数据的难度大为增加，故而通过无线传输方式实现井底测量信息的高效上传及地面指令的正确下达，至今仍是众多科研工作者致力攻克的热点难题之一。目前，常见的无线随钻测量技术（MWD）和无线随钻测井技术（LWD）都以钻井液柱为信息传输通道，这种利用钻井液脉冲波来实现井底测量数据传输的信息遥测方法虽然技术相对比较成熟，但其传输速率比较低，无法满足新一代随钻测井技术的高速率实时数据传输的要求[7-10]。智能钻杆通信技术的传输速率理论上可高达2 Mbit/s，是一种最为理想的井下信息传输方式[11-12]，但这种传输技术需要对现有钻杆进行重新设计和特殊改造，花费巨大，实现起来相当困难。研究表明以井下钻柱为信道，以正弦弹性波为载波的随钻声波遥测技术的信息传输速率可以高达100 bit/s，能够满足当前随钻遥测技术发展的需要，是目前国内外井下随钻测量数据无线传输领域的重要研究方向之一[13-14]。

然而，在由钻杆本体和接箍组成的周期性钻柱中传播时，声波具有衰减速度较快的特点，随着传播距离的增大，信噪比不断减小，这显然会给接收端的信号解调造成不良影响而使误码率增大，导致数据遥测质量下降，甚至出现严重差错。本文借助LabVIEW 编程语言，分别采用振幅键控、频率键控及相位键控3 种典型的二进制数字调制方法进行测井数据遥测模拟实验，测取信噪比与误码率之间的关系曲线，进而分析误码率对数据还原质量的影响。

1 数据遥测模拟实验

本文以某实际油井795.0～1873.4 m 井段的高分辨率阵列感应电阻率的实测数据（如图1 所示）为遥传对象。该测井数据序列的测量间隔为0.1 m，共计10785 个数据点；遥传前先将各数据点统一量化成由0 和1 码元构成的16 位二进制码组，再按先后顺序将这些码组串联成二进制码元序列，然后采用二进制振幅键控（2ASK）、频率键控（2FSK）及相位键控（2PSK）数字调制方式分别对载波的幅度、频率及相位3 个基本参量进行控制，进而以串行传输方式开展井下测量数据的无线传输模拟实验。

图1 原始曲线图Fig.1 Original curve

研究表明在钻柱中传播时，钻柱信道具有通阻交替的梳状滤波器特性，且信道的通带范围主要集中在1～5 kHz 之间，其中3 kHz 附近的频段表现最佳[15-16]，且纵波波速保持不变，本模拟实验以频率为3 kHz 的正弦波为载波；对于二进制振幅键控，初相位设定为0°，码元为0 时载波的幅度被调控为0，码元为1 时载波的幅度被调控为10；对于二进制频率键控，载波幅度设定为10，初相位设定为0°，码元为0 时载波的频率被调控为2.5 kHz，码元为1 时载波的频率被调控为3.5 kHz；对于二进制相位键控，载波幅度设定为10，频率设定为3 kHz，码元为0 时载波的初相位被调控为0°，码元为1 时载波的初相位被调控为180°。

钻井过程中，井下钻柱信道的噪声主要来源于钻头对岩石的破碎作用、钻柱与井壁及套管间的碰撞作用、钻井液的冲击作用及地面动力设备的振动作用等；这些噪声源均具备随机产生的特性，因此本实验选用高斯白噪声作为随钻声波遥测模拟实验的干扰噪声；其实，高斯白噪声本身就是通信领域最为常见的一种信号干扰噪声[17]。为直观展现信噪比与误码率之间的关系，本模拟实验在未对输出波形进行任何处理的条件下，利用LabVIEW 自带的波形信号虚拟检测仪来直接检测输出载波信号的相关参数，进而重现输入的二进制码元序列。具体的实现方法如下，分别取3 种键控方式的码元0和码元1 所对应的调控参数的平均值作为二进制码元还原的判决标准；即对于二进制振幅键控，若波形信号虚拟检测仪检测到的幅度参数小于5，则判决码元为0，若检测到的幅度参数大于等于5，则判决码元为1；对于二进制频率键控，若波形信号虚拟检测仪检测到的频率参数小于3 kHz，则判决码元为0，若检测到的频率参数大于等于3 kHz，则判决码元为1；对于二进制相位键控，若波形信号虚拟检测仪检测到的相位参数小于90°，则判决码元为0，若检测到的相位参数大于等于90°，则判决码元为1。解调出二进制码元序列后，根据原始数据的二进制量化方式实现井下测量数据的还原。图2 为数据遥测模拟实验的示意框图。

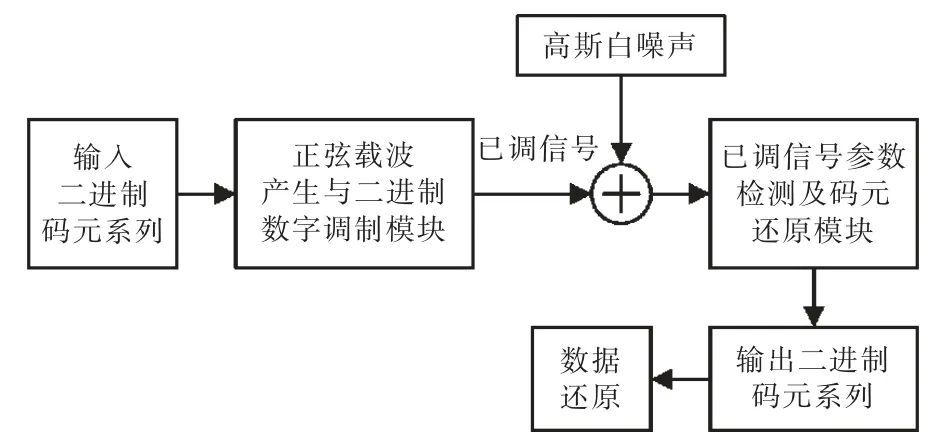
图2 遥传模拟框图Fig.2 Telemetry simulation block diagram

遥传模拟过程中，其它条件保持不变，仅通过改变高斯白噪声的标准差来获取不同的信噪比，信噪比（SNR）的计算公式如式（1）所示，以分贝（dB）为单位。

式中：Ps为载波的平均功率；Pn为高斯白噪声的平均功率；A 为载波的幅度；σ 为高斯白噪声的标准差。

图3 为二进制振幅键控、频率键控及相位键控3 种调制方式的遥测模拟实验结果的误码率与信噪比之间的关系曲线图。从图中可以看出，频率键控和相位键控的误码率与信噪比的关系曲线图比较相似，在相同信噪比下，二进制振幅键控的误码率最低。

图3 信噪比与误码率关系曲线图Fig.3 Relationship curve between signal-to-noise ratio and bit error rate

对于二进制振幅键控，当信噪比从0.34 dB 增大到11.88 dB 时，误码率由11.38%降低至0.10%，如图4（a）所示；当误码率小于等于0.10%时，遥测后的输出曲线与输入曲线具有很高的相似性，所反映的测井信息几乎没有损失；当误码率大于0.10%且小于0.75%时，遥测后的输出曲线会出现明显的零星突变点，且这种离散突变点主要发生于高数值曲线段，如图4（b）所示，此时，通过对零星突变点进行简单光滑处理后，曲线图形仍可以较为准确地反映出原始的测井信息；然而，当误码率大于0.75%时，遥测后的输出曲线开始出现较为严重的连续性突变，并且逐渐由高数值曲线段扩散至整个曲线段，如图4 中的（c）、（d）所示，曲线发生这种严重的连续性突变后，通过数据处理来修正并恢复遥测前的测井数据的可能性微乎其微。

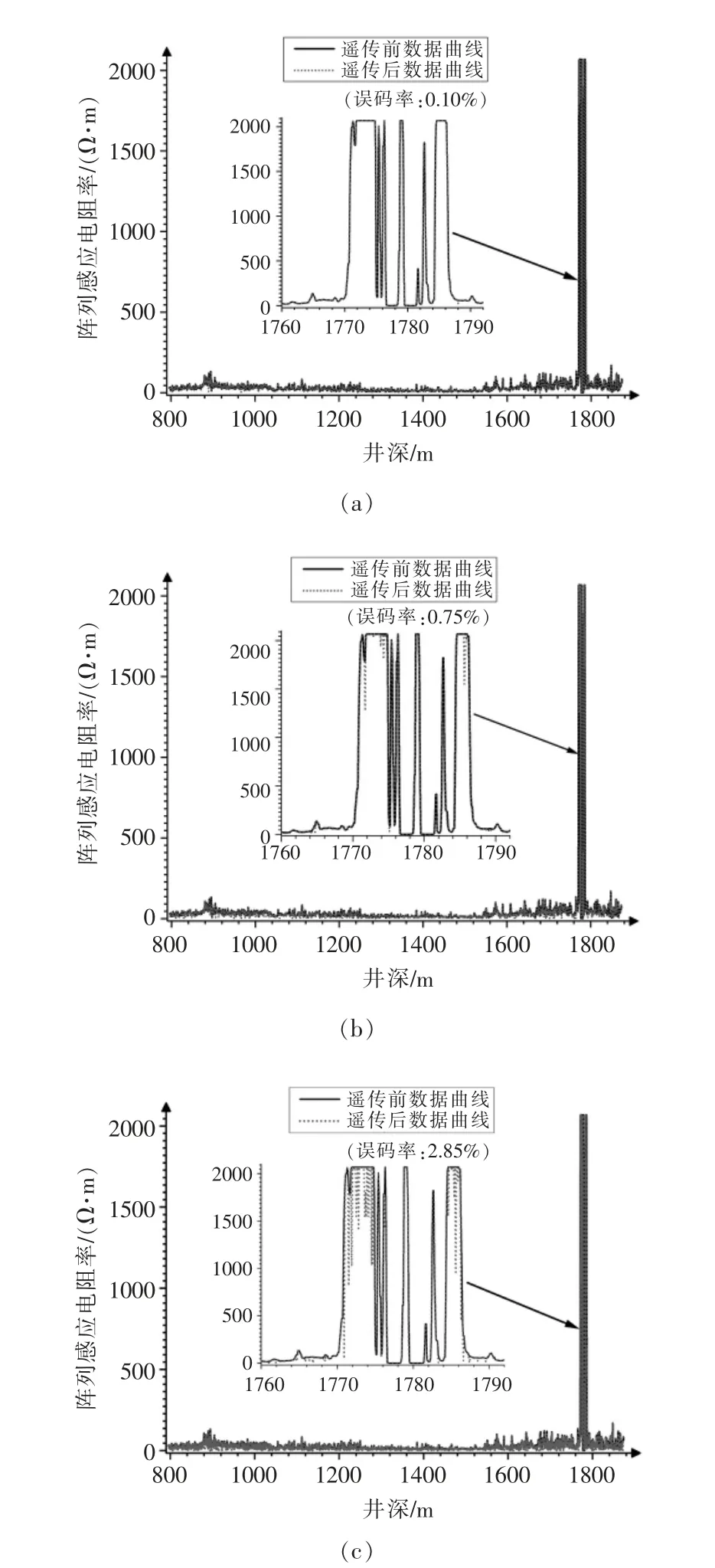
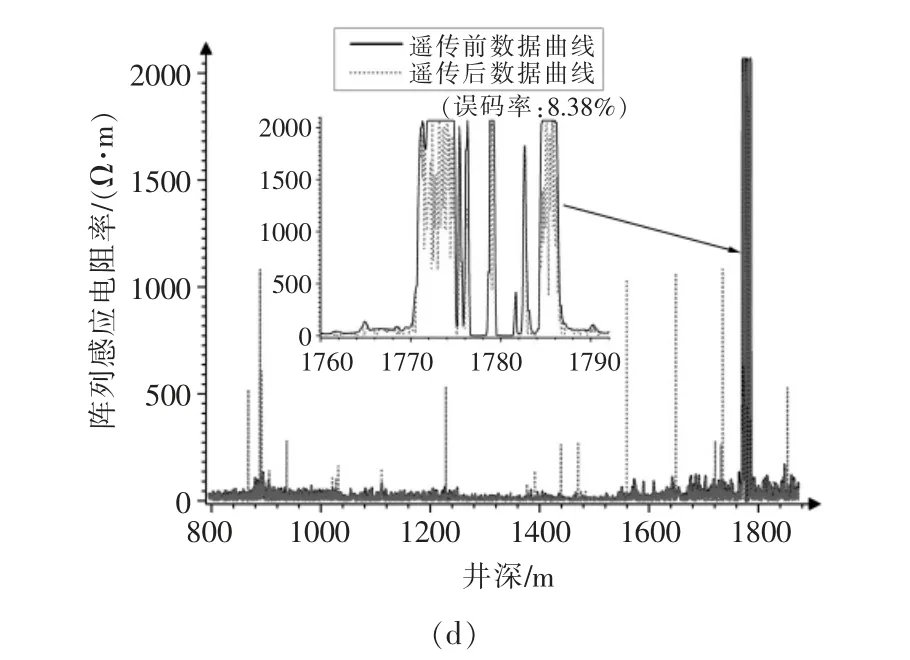
图4 误码率对数据还原质量的影响（二进制振幅键控）Fig.4 Influence of bit error rate on data recovery quality（binary amplitude keying）

对于二进制频率键控，当信噪比从0.34 dB 增大到13.47 dB 时，误码率由29.88%降低至0.01%，且误码率小于等于0.01%时，遥测后的输出曲线可以准确地反映出原始的测井曲线，如图5（a）所示，当误码率大于0.01%且小于0.09%时，遥测后的输出曲线会出现明显的零星突变点，但与二进制振幅键控不同的是，这些离散突变点主要发生于低数值曲线段，如图5（b）所示，此时，对这些零星突变点进行简单光滑处理后，曲线图形仍可以较为准确地反映出原始的测井信息；不过当误码率大于0.09%时，遥测后的输出曲线开始出现较为严重的连续性突变，并且逐渐由低数值曲线段扩散至整个曲线段，如图5 中的（c）、（d）所示，曲线发生这种严重的连续性突变后，要想从中准确提取出遥测前的测井数据几乎不可能。

图5 误码率对数据还原质量的影响（二进制频率键控）Fig.5 Influence of bit error rate on data recovery quality（binary frequency keying）

对于二进制相位键控，当信噪比从0.34 dB 增大到12.91 dB 时，误码率由28.91%降低至0.09%，如图6（a）所示，当误码率小于等于0.09%时，遥测后的输出曲线与原始测井曲线具有非常高的相似性，可以准确地反映出遥测前的测井信息；当误码率大于0.09%且小于0.93%时，遥测后的输出曲线会出现明显的零星突变点，类似于二进制振幅键控，这些离散突变点主要发生于高数值曲线段，如图6（b）所示，此时，对这些零星突变点进行简单光滑处理后，曲线图形仍可以较为准确地反映出原始的测井信息；然而，如图6 中的（c）、（d）所示，当误码率超过0.93% 时，遥测后的输出曲线开始出现较为严重的连续性突变，并且逐渐由高数值曲线段扩散至整个曲线段，曲线发生这种严重的连续性突变后，通过数据处理来准确提取遥测前的测井数据的可能性微乎其微。

图6 误码率对数据还原质量的影响（二进制相位键控）Fig.6 Influence of bit error rate on data recovery quality（binary phase keying）

2 结语

在本数值模拟实验的3 种典型二进制数字调制方式中，二进制振幅键控的测井数据遥测误码率的容忍度最高，为0.10%，二进制相位键控次之，为0.09%，二者的共同特点是，随着误码率的增大，都是从高数值曲线段开始发生明显的离散性突变，具有先干扰强烈变化曲线段的特点，而测井曲线的强烈变化部分往往包含着井下油气储层的重要物性信息，是钻井过程中需要高度重视的敏感井段。二进制频率键控的遥测误码率的容忍度最低，为0.01%，不过随着误码率的增大，其突变点从变化较为平缓的曲线段开始。另外，随着科技的快速发展，测井技术的分辨率越来越高，测井曲线上单一奇异变化点的参考价值极小，毕竟其对应的油气储层的厚度比较薄，工业开采价值比较低，况且这种奇异变化点大多都是因外界因素而非储层物性变化所引起的，因此储层物性曲线上的单一突变点通常都会被直接处理掉。实验发现，误码率在一定的范围内，遥测曲线也出现类似的离散性突变点，因此可以采用同样的方法将这些离散性突变点处理掉，而且还可以比较准确地还原出遥测前的测井数据；据此，储层物性遥测曲线的误码率的上限可以适当提高，信噪比的下限可以适当减小；如本实验，二进制振幅键控对应的误码率上限可以由0.10%提高至0.75%，信噪比的下限可以由11.88 dB 减小至9.39 dB；二进制频率键控对应的误码率上限可以由0.01%提高至0.09%，信噪比的下限可以由13.47 dB 减小至11.41 dB；二进制相位键控对应的误码率上限可以由0.09%提高至0.93%，信噪比的下限可以由12.91 dB 减小至10.55 dB；这一实验结果对遥传数据还原过程的处理方法具有一定的参考价值。另外，误码率是井下随钻遥测结果还原质量的决定性因素，而探究抗噪声干扰能力强的调制与解调方法是实现误码率降低的关键，也是当前随钻声波遥测技术急需解决的关键难题之一。尝试将当前比较热门的人工智能算法引进来，采取诸如寻找目标函数最优解的策略来实现遥测信号的解调，或许会有意想不到的收获，这正是本研究项目下一步研究工作的重点所在。